纠三错BCH码改进查找表译码算法研究及其实现∗

孔挺 余鹏 王浩

（海军航空兵学院 葫芦岛 125001）

1 引言

BCH码是目前已知的一类可以有效纠正多个独立错误的循环码，这类码具有简单的结构、较强的纠错能力，在信道纠错码领域得到了广泛应用。相较BCH码的编码而言，其译码要复杂得多，因此，寻找简单、快速、易于实现的BCH码译码算法一直是几十年来编解码研究领域关心的热点之一。到目前为止，较为著名的BCH码译码算法主要包括Peterson算法［1］、PGZ算法［2］、Chien搜索算法［3］、Forney 算法［4］、BM 迭代算法［5～6］、IBM 算法［7］等，其中，以BM迭代算法和Chien搜索算法最为有效［8］，然而，当码字出错位数增加，上述算法将需要大量复杂的代数运算，从而造成译码慢、电路复杂等问题。此外，还有一种查找表算法，它将码字出现不超过其纠错能力时所有错误图样与对应的校验子存储在查找表中，通过计算接收码字的校验子直接找到相应的错误图案，实现纠错，与前述算法相比，它具有计算量小、结构简单、易于实现的优点，但是随着码字的码长增加和纠错能力提高，其占用存储资源较大的问题将变得非常突出，因此，这种算法主要用于中短码长的BCH码。对于查找表算法的优化和应用，国内外一些专家学者也开展了相关研究［9～11］。其中，文献［10］提出了利用校验子的码重参与译码的缩短查找表算法，该算法以纠三错的（15，5，7）BCH码和（31，16，7）BCH码为例，只把信息位出2位以下错时的错误图样和对应的校验子存储在查找表中，利用BCH码是循环码的特点，通过计算校验子码重来纠错，该算法虽然比传统查找表算法节省较多的存储资源，但在信息位有1位出错、校验位有2位出错的情况下，需要很多次循环运算，因而计算量过大，导致译码速度大幅下降；文献［11］针对纠二错BCH码，把信息位出2位以下错时的错误图样和对应的校验子存储在查找表中，虽然也通过计算校验子码重来纠错，但不需循环运算，因此，在大幅降低资源消耗的同时，使译码速度得到了有效的提升。基于文献［11］中的改进算法的思想，本文以（15，5，7）BCH码为例，研究该算法在纠三错BCH码中的应用及性能表现，并基于FPGA研究其实现方法。

2 传统查找表算法原理

传统查找表算法的原理是基于接收码字R的校验子S与错误图样E之间存在着对应关系，根据两者间的这种关系，建立一个查找表，将所有可能的校验子和相应的错误图样存储在查找表中，译码时将计算得到的校验子与查找表中的数据进行查找对比，找到相同的校验子即可得到错误图样，从而确定R的错误位置并加以纠正［11］。具体而言就是：

1）当 S=0时，说明 e1=e2=…=en=0，即E=0，R=C，说明R无错误。

2）当 S≠0 时，说明 e1，e2，…，en不全为0，即 R至少存在1位错误，根据校验子的值与监督矩阵H中列向量的对应关系，按以下方法确定R的错误位置：

（1）当R存在1位错误时，假设是R的第i位出错，那么 ei=1，el=0（l=1，2，…n，l≠i），则 S向量应等于H矩阵的第i列向量，利用这个关系就能够找到R的出错位置。

（2）当R存在2位错误时，假设是R的第i、j两位出错，那么 ei=ej=1，el=0（l=1，2，…，n，l≠i，j），则S向量应等于H 矩阵的第i列和第 j列向量的模2和，且这两列的取法具有唯一性，利用这个关系就能够找到R的2个出错位置。

同理，按照上述方法，只要R的出错位数在BCH码的纠错能力范围内，就可以根据S向量与H矩阵的列向量的对应关系对R进行纠错。

上述算法在具体实现时，只须用一块ROM存储校验子和相应的错误图样，译码时将计算得到的校验子与查找表中的校验子进行逐一对比，找到相同的校验子，便可得到相应的错误图样，实现纠错［12］。以（15，5，7）BCH码为例，该码可以纠3位错，因此，其ROM中需要存储=575组数据，每组数据中S向量与E向量分别占用2 bytes的存储空间，即共需占用4 bytes的存储空间。

由此可知，传统查找表算法因无迭代或循环运算，其译码速度快、硬件实现也比较简单。但是，它也存在明显的不足：当码字较长或码字的纠错能力强时，会占用较多的存储资源。因此，这种算法更适用于短或中等长度码字的译码。

3 基于查找表的改进算法原理

文献［11］以可以纠正两位错误的（31，21，5）BCH为例，基于传统查找表提出了一种改进的译码算法，不仅节约了存储资源，还提升了译码速度。借鉴该算法的思想，下面以（15，5，7）BCH码为例，研究该算法如何实现纠三错BCH码的译码。

假设（15.5.7）BCH码采用系统码，接收码字为R=(r2，…，r15)，其中 r1～r5为信息位，r6～r15为校验位，校验子 S=R·HT=E·HT=[PTI10]。根据改进查找表算法的思想，应把（15，5，7）BCH码信息位出3位以下错时的错误图样和对应的校验子图样（统称为查找图样）存储在查找表中，则查找表中总共应存储=25个查找图样，每个查找图样中S向量为10 bits，E向量为15 bits，均需占用2 bytes的存储空间，因此，一个查找图样需占用4 bytes的存储空间。

与传统查找表算法一样，在码字最多只发生3位错误的前提下，S应该等于监督矩阵H中某些与错误位置对应的列的模2和，改进算法确定接收码字出错位置的原则如下：

1）信息位无错，仅校验位出错的情况：如果校验位r6～r15有1位出错，因为H对于码字校验位的后半部分是单位阵，所以此时校验子S的码重w(S)=1；同理，校验位有2位出错时，码重w(S)=2；校验位有3位出错时，码重w(S)=3。并且在上述错误情况下，S中1的位置与r6～r15中的出错位置一一对应，可以直接纠错。

2）仅信息位出错，校验位不出错的情况：此情况下，码重w(S)≥3，但由于信息位只发生1位～3位以下错误的错误图样和对应的校验子图样已经存储在查找表中，只需搜索查找表就可找到对应的错误图样，进行纠错。

3）信息位和校验位都出错的情况：假设信息位有1位出错误，校验位有1位或2位出错，S与查找表中对应的校验子图样Si求模2和后得到的的码重w()应等于1或2，且中1的位置与码字校验位出错的位置对应；假设信息位有2位出错，校验位有1位出错，S与查找表中对应的校验子Si求模2和后得到的的码重应等于1，同样，中1的位置与码字校验位出错的位置对应。

根据上述原则，（15，5，7）BCH码采用改进查找表算法的译码流程如图1所示，图中“选择满足唯一纠错条件的”中的“纠错条件”是：S与信息位发生1位错误时对应的Si求模2和所得的的码重w(≤2；S与信息位有2位出错时对应的Si求模2和所得的的码重w(≤1；S与信息位有3位出错时对应的Si求模2所得的的码重w(=0。

4 算法性能分析

4.1 资源消耗

（15，5，7）BCH码分别采用不同算法时的存储资源消耗情况见表1。

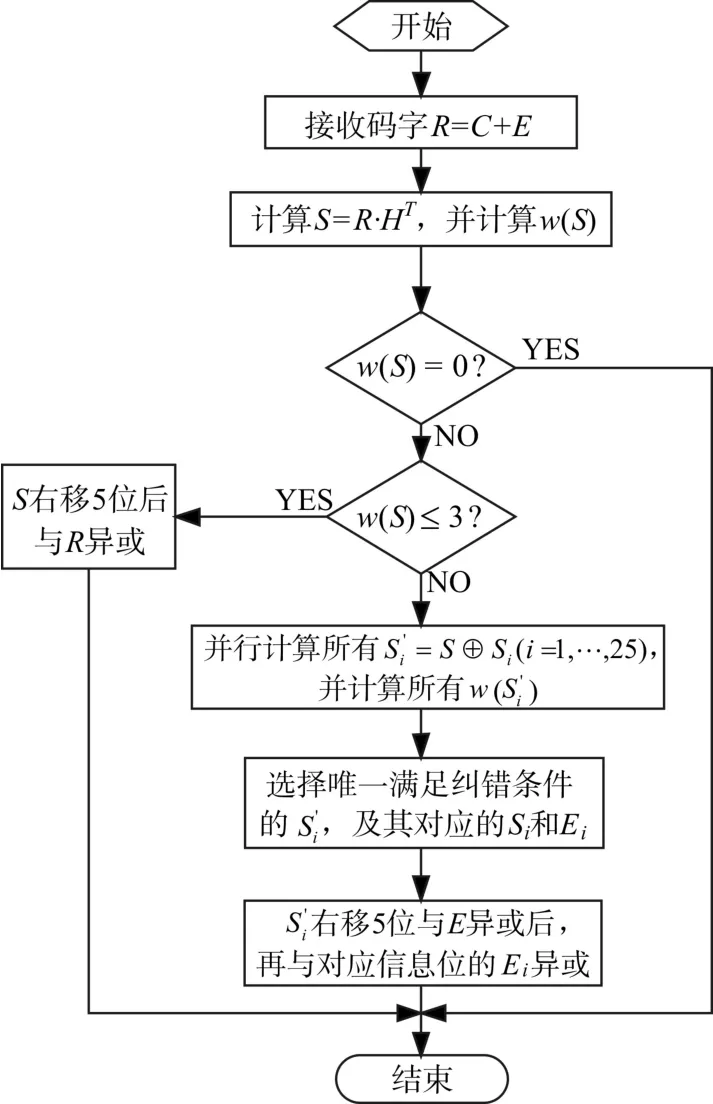
图1 改进算法的译码流程

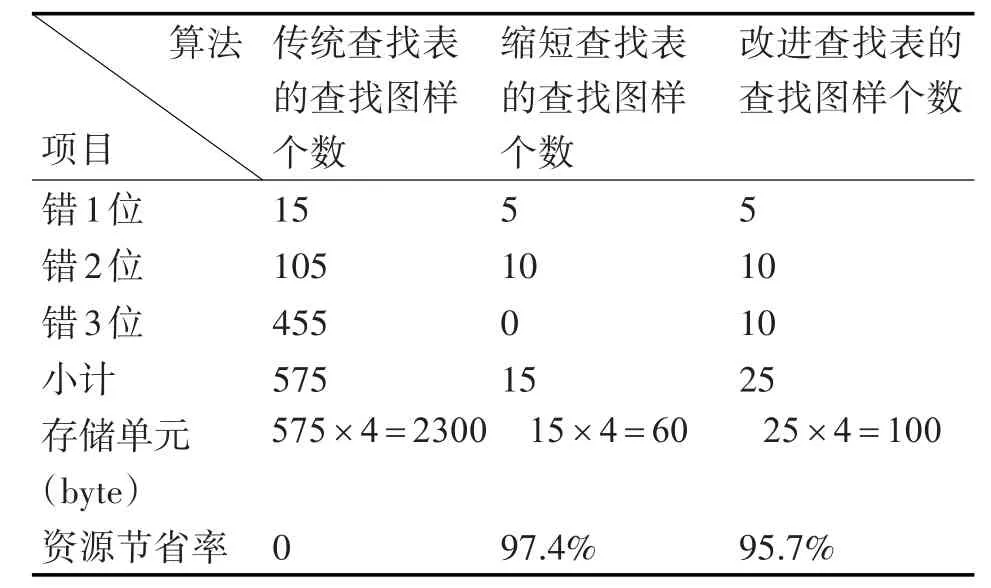
表1 不同查找表算法的存储资源消耗

从表1数据可以看出，相对传统查找表算法而言，文献［10］提出的缩短查找表算法仅将码字信息位出现两位以下错误时的查找图样存储在查找表中，因而其资源节省率最高，而改进查找表算法因在查找表中比它多存储了信息位出现三位错误时的查找图样，导致其资源节省率略低于缩短查找表算法，但仍然远高于传统查找表算法。

4.2 译码性能

图2所示为译码性能的仿真模型。图中，设定AWGN信道的信噪比（EbNo）为2.5dB，采用两种算法译码时均随机生成10万帧信息位码字。仿真计算机处理器为 Intel（R）Core（TM）2 Duo CPU T6500 2.10GHz；计算机系统内存为2GB。仿真结果如表2所示。

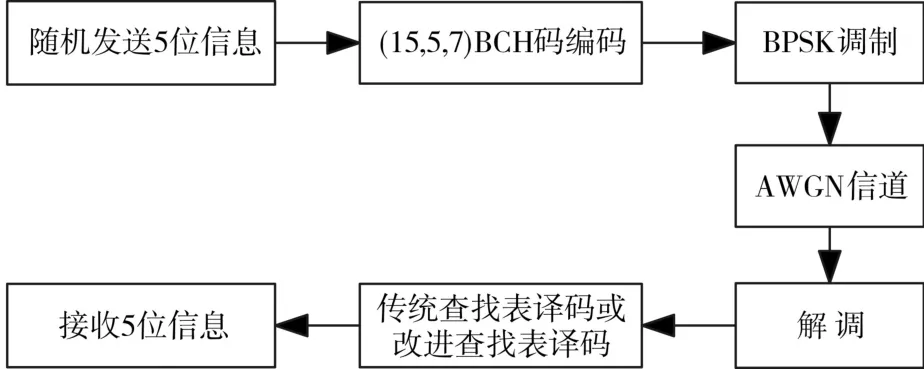
图2 仿真模型

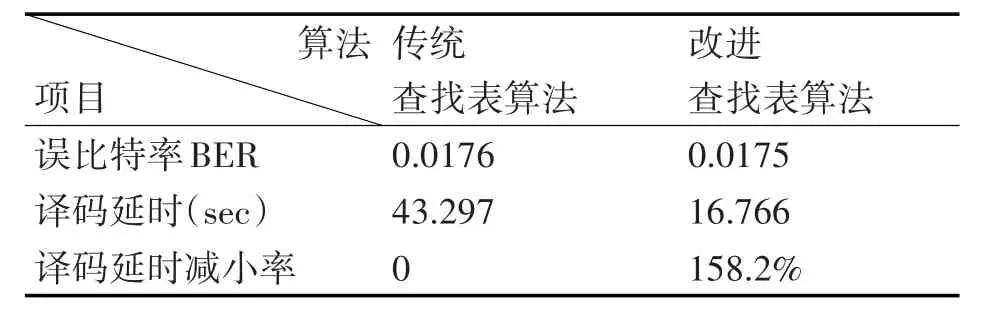
表2 传统与改进查找表算法的译码性能

从表中的数据可以看出，（15，5，7）BCH码采用两种译码算法时的BER性能相当，这说明改进查找表算法适用于可纠3位错的BCH码。但是，由于改进查找表算法的查找表中查找图样比传统查找表少得多，因此，其译码延时比传统查找表算法减小了近1.6倍；而文献［10］缩短查找表算法的查找表中的查找图样虽然比传统查找表算法和改进查找表算法都少，但是其译码过程中需要利用循环码的循环移位特性进行多次循环移位计算，因此，其译码速度较慢，译码延时几乎是传统查找表算法的10倍。

此外，对比文献［11］的表1的仿真结果可知，BCH码的纠错能力、信息位长度对改进查找表译码速度的提升有较大影响。

5 改进查找表算法的FPGA实现

5.1 设计方案

采用改进查找表算法译码的实现框图如图3所示。其中输入码字为在Matlab随机生成的（15，5，7）BCH码码字，经随机加3位以下错误后形成的待译码数据。

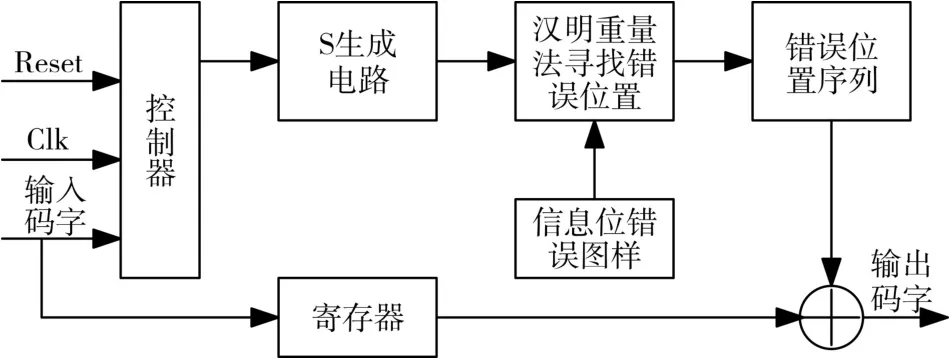
图3 改进查找表译码的FPGA实现框图

为了提高译码速度，码字的传输采用比特并行方案，如图4所示，图中，nbits数据 bn，…，b2，b1在一个时钟、n条线上并行发送。具体而言就是，每个时钟完成一个15bits的（15，5，7）BCH码字的接收，并存储于寄存器内，等待与错误序列进行异或。

图4 码字传输比特并行方案示意图

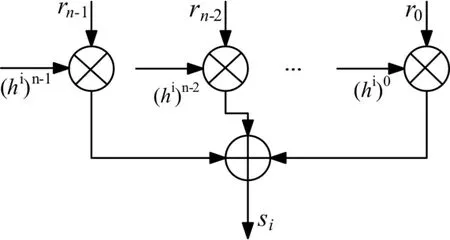
图5 校验子比特si的实现电路

利用容量为25×25，地址线和数据输出线数量分别为5根、15根的ROM存储25个10bits大小的校验子和5bits大小的错误图样。计算得到S后，按照图1的改进算法流程找出错误图样，对输入码字纠错后输出译码码字。

图6为基于Quartus软件平台构建的系统顶层框图，利用VHDL编程将其封装成图形形式，图中从左至右依次为控制模块、纠错模块和输出模块［15］。译码器采用Altera公司的cycloneⅡ系列的EP3C5F265C6芯片实现。

图6 译码电路系统顶层框图文件

5.2 仿真结果

根据Quartus软件最终的综合编译报告结果，该译码器对任意3bits的错误组合图样均可正确纠错，译码过程共占用593个逻辑单元（占用率12%）；在50MHz时钟下，译码器可在2个时钟内完成译码，译码时序仿真结果如图7所示。

图7 译码电路时序仿真图

6 结语

在BCH码传统查找表译码算法的基础上，以（15，5，7）BCH码为例，研究了文献［11］提出的改进查找表算法对可纠正3位错误的BCH码的译码原理和流程，仿真比较了该算法与传统查找表算法的译码性能，并基于FPGA研究了该算法的硬件实现方法。研究表明，改进算法与传统查找表算法在BER性能上一致，但前者在资源消耗和译码速度性能上的表现明显优于后者；设计的译码器具有结构简单、资源占用少、运行速度快的特点，非常适合中短码长BCH码在硬件设备受限或高速数据传输系统中的应用。

［1］W.W.Peterson.Encoding and Error-Correction Proce⁃dures for the Bose-Chaudhuiri Code［J］.IRE Trans.In⁃form.Theory，1960，6：459-470.

［2］ D.Gorenstein，N.Zierler.A Class of Cyclic Linear Er⁃ror-Correcting Codes in pm Symbols［J］.J.Soc.Ind.Appl.Math，1961，9：207-214.

［3］ R.T.Chien. Cyclic Decoding Procedure for the Bose-Chaudhuri-Hocquenghem Codes［J］.IEEE Trans.Inform.Theory，1964，10：357-363.

［4］G.D.Forney.On Decoding BCH Codes［J］.IEEE Trans.In⁃form.Theory，1965，11：549-557.

［5］ E.R.Berlekamp.On Decoding Binary Bose-Chaud⁃huri-Hocquenghem Codes［J］.IEEE Trans.Inform.Theo⁃ry，1965，11：577-580.

［6］J.L.Massey.Shift-Register Synthesis and BCH Decoding［J］.IEEE Trans.Inform.Theory，1969，15（1）：122-127.

［7］H.O.Burton.Inversionless Decoding of Binarry BCH Codes［J］.IEEE TRrans.Inform.Theory，1971，17（4）：464-466.

［8］Shu Lin，Daniel J.Costello，Jr著.晏坚等译.差错控制编码（第2版）［M］.北京：机械工业出版社，2007：130.

Shu Lin，Daniel J.Costello.Jr.Error Control Coding（2nd ed）［M］.Beijing：Machine Industry Press，2007：130.

［9］李雄飞，李振华，邱乐德.缩短BCH码（16，8，5）编译码算法及其实现［J］.空间电子技术，2009，6（2）：33-38.

LI Xiongfei，LI Zhenhua，QIU Lede.A Coding and Decod⁃ing Algorithm and its implementation of shortened BCH Codes（16，8，5）［J］.Space Electronic Technology，2009，6（2）：33-38.

［10］H.P.Lee，H.C.Chang，T.C.Lin，T.K.Truong.A Weight Method of Decoding the Binary BCH Code［C］//8th International Conference on Intelligent Systems De⁃sign and Applications.IEEE Computer Society，2008：545-548.

［11］孔挺，宫芳，方扬扬.基于查找表的BCH码快速译码算法［J］.哈尔滨商业大学学报（自然科学版），2011，27（6）：819-823.

KONG Ting，GONG Fang，FANG Yangyang.A fast de⁃coding Algorithm for BCH codes based on lookup table［J］.Journal of Harbin University of Commerce（Natural Sciences Edition），2011，27（6）：819-823.

［12］周盛容，胡正飞.基于BM迭代的高速BCH译码方法［J］.电脑知识与技术，2007（4）：1019-1020.

ZHOU Shengrong，HU Zhengfei.Fast BCH decoding de⁃sign using BM iteration［J］.Computer Knowledge and Technology，2007（4）：1019-1020.