具有多重休假策略和可修性质GI/Gemo/C/∞排队模型∗

甘 娜 黄裕锋 陆晓梅

（广东工程职业技术学院信息工程学院 广州 510520）

1 引言

排队系统在实际生活中非常普遍，如何提高排队系统的服务性能，降低人力运营成本，对于排队系统的优化具有实际应用意义。目前，很多学者对休假和可修排队模型进行了研究。参考文献［1］提出一种以概率P进入和服务时间为Erlang分布的可修排队模型，参考文献［2］提出基于多重休假的min（N，V）-策略M/G/1排队系统的队长分布，参考文献［3］提出了N策略带启动时间的Geom/Geom/1工作休假排队。然而，很多研究学者主要关注的是休假或可修排队模型，对多重休假策略和可修性质相结合的排队模型关注极少。

本文从排队系统服务台多重休假和可修的特点为改进方向，在Erlang排队模型的基础上，建立了空竭服务多重休假的GI/Gemo/C/∞可修排队模型。对排队系统服务过程进行仿真，仿真结果验证了空竭服务多重休假的GI/Gemo/C/∞可修排队系统的合理性及有效性，提高了服务台利用率，减少了服务等待时间。

2 Erlang-A排队模型及改进

2.1 Erlang-A排队模型

Erlang-A的通用性需要四个参数：到达为固定速率λ的Poisson分布；服务服从服务率μ的指数分布；坐席数目C；顾客耐心等待时间1/θ，并假定其服从指数分布。Erlang-A对应的排队模型为M/M/C/∞ 。系统的负载为 α=λ/μ ，如果 α≥C ，则系统超过系统的处理能力，出现无穷排队，顾客的等待时间趋向于无穷大。一般主要分析在α＜C的状态下，排队等待时间的分布情况［4～6］。

在所需的各种经验参数都很准确、且满足到达、服务持续时间符合前提分布的情况下，Er⁃lang-A模型对系统性能参数的估计较精确。但Er⁃lang-A模型考虑了客户的等待时间问题，但并不能完全解决客户的满意度问题，仅仅适合轻负载排队系统性能分析［7～8］。基于此，针对该模型的缺陷进行改进，建立一种新排队模型来弥补它的不足。

2.2 改进的Erlang-A排队模型

为了提高客户的满意度，不仅要考虑客户的等待时间问题，还要考虑服务台人员的排班问题，例如：服务台休假、服务台修理问题，降低服务成本。基于上述因素的考虑，本文在Erlang-A排队模型的基础上，考虑到服务时间为离散事件，将排队系统服务时间分布推广为离散型概率分布几何分布［9～11］，并引入多重休假策略、可修性质，建立了一个空竭服务多重休假的GI/Gemo/C/∞可修排队模型。

假设到达间隔、服务时间、休假时间相互独立；顾客的到达间隔时间是相互独立同分布的正整值随机变量；顾客实际所需的服务时间相互独立并服从几何分布；服务台具有空竭服务的多重休假规则；系统中有C个服务台，使用FIFO排队规则。为了使休假期间内发生的顾客到达时刻具有Markov性质，假设休假时间V服从几何分布：

P{V=j}= θθˉj-1，j≥ 1，0＜ θ ＜ 1， θˉ=1- θ

约定休假的开始和结束都发生在时隙末端，C个并行的服务台，系统中有无限的等待场所，休假期间服务台完全停止对顾客的服务。

空竭服务多重休假的GI/Gemo/C/∞可修排队系统具体的描述如下：

1）顾客在时刻 t1，t2，… 分别以批量 ξ1，ξ2，… 成批陆续到来，到达时间间隔τn=tn+1-tn，(n=1，2，…)独立同分布随机变量，分布函数为F(t)=p{τn≤t}，t＞0，n≥1，而且平均到达时间间隔有 0＜1/λ=tdF(t)＜+∞ 。顾客到达间隔是相互独立同分布的正整值的随机变量，记为T，有概率分布和PGF：

2）批量 ξn，n≥1为取正整数值的i.i.d随机变量 ，设 P(ξn=i)=bi，n≥1，i=1，2，… ，均 值 为bˉ≜Eξi＜+∞，i=1，2，…n ；

3）第n批到来的顾客中第k个顾客接受服务系 统 的 服 务 时 间 为 Vnk，k=1，2，…，ξn且(Vnk，n=1，2，…，k=1，2，…，ξn)为i.i.d随机变量序列，分布函数为G(t)=P{Vnk≤t}，t≥0，n≥1，且令平均服务时间有 0＜α=tdG(t)＜+∞（即每位顾客的服务时间独立同分布G(t)。顾客服务时间S1相互独立并服从几何分布

4）服务规则为先到先服务，且同批到达顾客的服务次序是任意的。一个话务员，每次只服务一个顾客；

5）假定服务台的休假时间序列{Vi，i≥1}相互独立、服从相同任意分布V(t)，并且独立于到达和服务过程；

6）服务台可修，服务台的寿命长度X服从分布 X(t)=1-e-at，t≥0。服务台失效后的修理时间Y服从一般分布Y(t)=P{Y≤t}，t≥0，而且平均修理时间为 0＜β=tdY(t)＜+∞。进一步假定服务台在空闲时间不会失效；当服务台失效时，正在接受服务的顾客需等待其修复后再继续接受服务，已服务过的时间仍然有效，即累积计算；服务台修复如新，并能立即投入使用；

7）到达间隔τn，各个顾客服务时间Vnk，到达批量ξn及失效后的修理时间Y均相互独立。

3 系统性能指标分析

3.1 排队系统性能指标

设系统交通强度 ρ=(cμE(T))-1＜1，L-表示的稳态极限，称为该排队系统到达前夕的稳态队长。稳态分布记为

实际上，空竭服务多重休假的GI/Gemo/C/∞可修排队系统的这些指标与无休假的M/M/C/∞系统相同，于是有：

稳态下时刻n+处的队长L+，可得到稳态队长L+的PGF：

定理1ρ＜1时，M/M/C/∞排队系统中稳态等待时间有PGF：

证明 如果稳态下到达的顾客遇状态 j(≥c)，其等待时间大于k意味着c个服务台都工作，k个时隙上完成服务不超过 j-c个。因此，

容易得出式（2）。得证。

由定理1可知，对于空竭服务多重休假的GI/Gemo/C/∞可修排队系统稳态下的平均等待时间，有

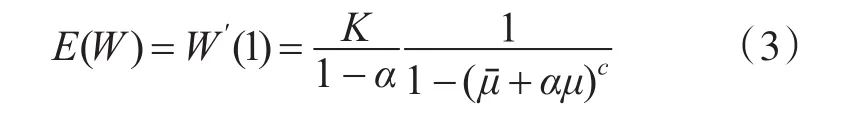
3.2 服务台可靠性指标

1）系统的可用度

定义服务台可用度为服务台处于服务期（非休假和故障）的概率。由模型的假设及忙期的定义，在一个忙期内，服务台依次处于“完好工作”和“失效修理”两种状态。

对t≥0，令

Ai(t)=P{时刻t处于服务员忙期|N(0)=i}，

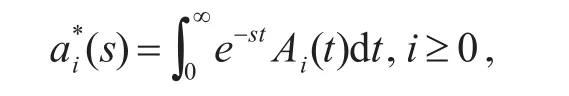
其中N(0)表示t=0系统中的顾客数。

定理2 对复变量s的实部ℜ(s)≥0，有

而且平稳结果

在空竭服务多重休假的GI/Gemo/C/∞可修排队系统中，对ℜ(s)＞0，服务台的瞬态可用度的L变换为

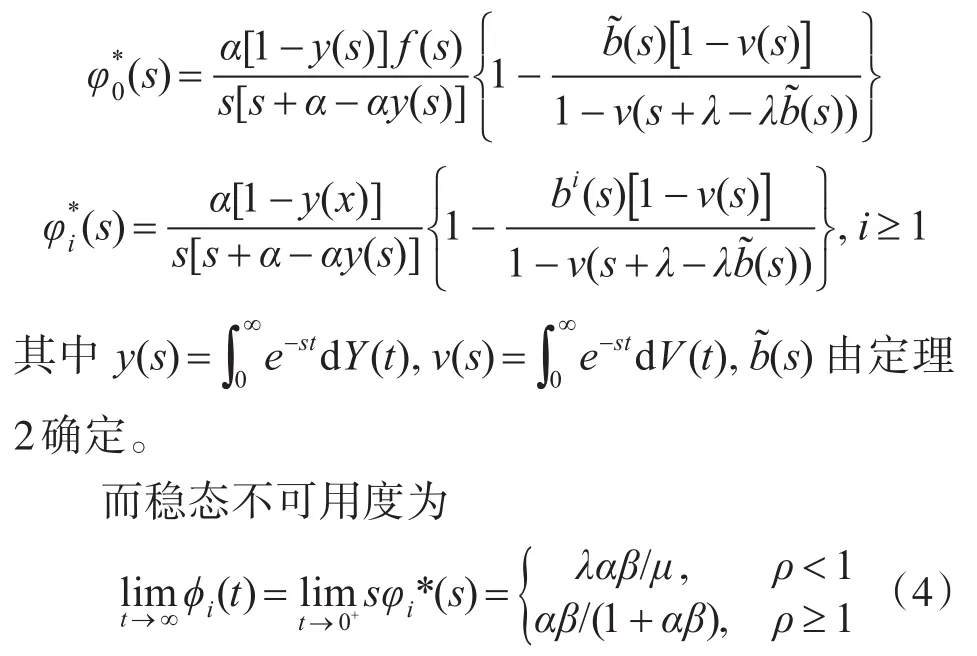
2）系统的故障频度

系统在单位时间内的故障次数，即故障频度，也是我们所关心的重要可靠性指标，它反映了系统的优劣。

定理3 对ℜ(s)＞0，服务台(0，t]内平均失效次数的LS变换为

对于空竭服务多重休假的GI/Gemo/C/∞可修排队系统，由定理3可知：

长期单位时间内的平均失效次数为

4 数值实验结果和图形分析

本文通过Matlab平台对基于空竭服务多重休假的GI/Gemo/C/∞可修排队模型的排队系统建模，输入参数有如下设定：每个时隙顾客到达概率为0.1～0.9；每个时隙服务完成概率为0.1～0.5；服务台个数为1～32。根据第3.1节和第3.2节得到的稳态指标均值的概率表达式及排队系统的性能分析指标，通过数值例子分析出系统参数对系统性能指标的影响，可以得出各种相关的性能指标变化曲线。

图1 平均等待时间随服务率变化的曲线

图2 平均队长随服务率变化的曲线

图3 系统交通强度随平均到达间隔变化的曲线1

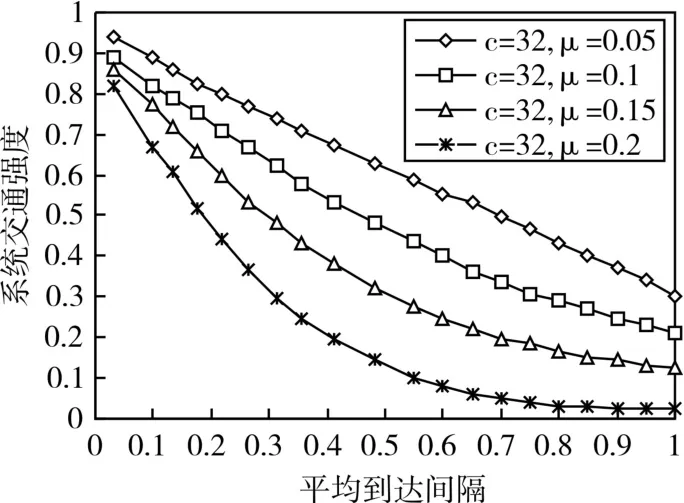
图4 系统交通强度随平均到达间隔变化的曲线2

从图1～图6中可以得出下列规律：图1和图2说明随着服务率的增大，平均等待时间和平均队长逐渐减小，并且平均等待时间和平均队长随着服务台个数的增多而减小。图3说明在服务率不变的前提下，系统交通强度随着服务台个数的增多、平均到达间隔的增大而减小。图4说明在服务台个数不变的前提下，系统交通强度随着服务率和平均到达间隔的增大而减小。图5说明在服务台个数不变的前提下，系统不可用度随着到达率和系统交通强度的增大而增大。图6说明服务台平均失效次数随着到达率和系统交通强度的增大而增大。

图5 系统不可用度随系统交通强度变化的曲线

图6 系统平均失效次数随系统交通强度变化的曲线

5 结语

本文针对传统Erlang排队模型在重负载的条件下服务持续时间不能服从指数分布的问题，提出了基于空竭服务多重休假的GI/Gemo/C/∞可修排队模型，利用嵌入马尔可夫链理论方法研究基于空竭服务多重休假的GI/Gemo/C/∞可修排队模型，得到了排队模型的平稳分布及相关性能指标。结合数值例子，获得了该模型在排队应用中的相关指标及各个性能指标之间的关系；根据得出的实验结果，验证了改进的排队模型的合理性，该模型既提高排队系统客户满意度，又降低了服务成本。

［1］谭秀辉.以概率P进入和服务时间为Erlang分布的可修排 队 模 型［J］.科 学 技 术 与 工 程 ，2010，10（5）：1204-1205.

TAN Xiuhui.A repairable queueing model with probabili⁃ty P and Erlang distribution［J］.Science Technology and Engineering，2010，10（5）：1204-1205.

［2］唐应辉，吴文青，刘云颇，等.基于多重休假的min（N，V）-策略M/G/1排队系统的队长分布［J］.系统工程理论与实践，2013，36（4）：1533-1534.

TANG Yinghui，WU Wenqing，LIU Yunpo，et al.Queue length distribution of M/G/1 queueing system with min（N，V）-policy based on multiple server vacations［J］.Systems Engineering Theory&Practice，2013，36（4）：1533-1534.

［3］朱翼隽，潘小春，胡彬.N策略带启动时间的Geom/Geom/1工作休假排队［J］.应用数学与计算数学学报，2010，24（1）：26-27.

ZHU Yijun，PAN Xiaochun，HU Bin.Geom/Geom/1 Queue with Working Vacations and N-policy and Set-up Time［J］.Comm.on Appl.Math.and Comput，2010，24（1）：26-27.

［4］C G Park，D H Han.Comparison of loss formulas for a cir⁃cuit group with overflow traffic［J］.Journal of Applied Mathematics and Informatics，2012，30（1-2）：135-145.

［5］孙健，丁日佳，陈艳艳.M/M/c型与M/M/1型排队系统对比仿真［J］.北京工业大学学报，2016，42（9）：1325.

SUN Jian，DING Rijia，CHEN Yanyan.Comparative Simu⁃lation on M/M/c and M/M/1 Queuing Systems［J］.Journal Of Beijing University of Technology，2016，42（9）：1325.

［6］G_Choudhury.An M/G/l Queue with Two Phases of Ser⁃vice Subject to the Server Breakdown and Delayed Repair［J］.Applied Mathematical Modeling，2009，16（33）：2699-2709.

［7］李惠.M/M/2排队系统的阀值和休假策略的研究［D］.秦皇岛：燕山大学，2015.

LI Hui.Research on M/M/2 Queueing System With Threshold And Vacation Policies［D］.Qinhuangdao：Yan⁃shan University，2015.

［8］Jishen Jia，Shaomin Wu.A replacement policy for a repair⁃able system with its repairman having multiple vacations［J］.Applied Mathematics and Computation，2011，21（217）：4994-4998.

［9］任鹏月.带启动—关闭期、多重工作休假的离散时间Geom/Geom/1排队模型［D］.长沙：中南大学，2014.

REN Pengyue.A discrete time Geom/Geom/1 queue mod⁃elwith multipleworking vacation and set-up and closed-down period［D］.Changsha：Central South Univer⁃sity，2014.

［10］Lee D H，Yang W S.The N-policy of a discrete time Geo/G/1 queue with disasters and its application to wire⁃less senor networks［J］.Applied Mathematical Model⁃ling，2013，37（23）：972-976.

［11］Wang J T，Huang Y B，Tien V D.A single server dis⁃crete time queue with correlated positive and negative customer arrivals［J］.Applied Mathematical Modelling，2013，39（9）：332-361.