微电网中分布式电源能量优化管理研究

徐敦彬 郝 威 王永力 袁光伟

（国网江苏省电力公司徐州供电公司 徐州 221005）

1 引言

分布式电源通过微电网的形式接入电网逐步成为了一种有效的特殊手段［1］，并且在电力研究领域分支中引起了广泛关注［2］，鉴于分布式电源在并网过程中的复杂性，微电网的规划设计和运行模式已经成为智能电网技术的重要组成部分［3］。分布式电源在接入母线的过程中会对配电网产生严重的线损现象［4～6］，在储能蓄电池对并网后的电能进行集中时，其损耗主要表现为电压损耗和功率损耗［7］，过多的损耗使得微电网的电源能量大量的浪费［8］。本研究针对微电网中的分布式电源并网能量最优化问题，通过光伏发电系统、风力发电系统、微型燃气轮机和储能蓄电池组组合成为微电网研究对象，建立最优化问题目标函数度量求出的目标函数电压损耗最小和功率损耗最小的表达式，并以光伏发电系统为例进行目标函数的推导。在对实验算例推到求解过程中使用拉格朗日函数给出了电源最优条件下的驻点处的函数值，精确地计算出了不同机组的各分支线路的损耗对最终电源能量优化的影响。

2 微电网结构与模型

2.1 微电网结构

假设线路为单电源辐射状网络，微电网结构中包含n1个光伏发电系统、n2个风力发电系统、n3个微型燃气轮机和一个储能装置。为不失一般性，在n1个光伏发电系统中从第1个到第d1个光伏发电系统不带有负载，第(d1+1)个到第n1个光伏发电系统带有负载；在n2个风力发电系统中从第1个到第d2个风力发电机组不带有负载，第(d2+1)个到第n2个带有负载；在n3个微型燃气轮机中从第1个到第d3个微燃机不带负载，第(d3+1)个到第n3个微燃机是带有负载，微电网组合形式如图1所示。

图1 微电网组合

2.2 最优分配模型

最优化问题用数学方法进行描述时，包含了目标函数、决策变量和约束条件这三个要素［9］。其中，目标函数度量解的优劣程度，如成本、收益、利润等［10～12］；而决策变量为可以调节、影响优化过程的变量；约束条件指决策变量及其相互关系的约束。最优化问题的一般形式为

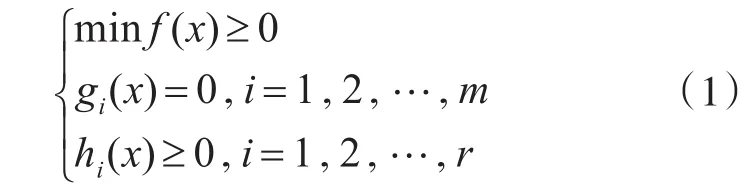
其中，x∈Rn为决策变量；f(x)为目标函数；gi(x)=0为等式约束；hi(x)≥0为不等式约束。

3 分布式电源能量优化

3.1 电源负荷优化

本文主要从技术目标最优出发，对微电网进行优化，先构造微电网目标函数，然后建立微电网运行约束条件。微电网的等效电路图可运用欧姆定律、基尔霍夫定律等直接写出有关的计算公式［13］。但这些方法都不免进行复数运算，不利于手算，而手算时应尽可能避免复数运算的方法［14］。因此本文所求出的目标函数电压损耗最小和功率损耗最小的表达式，最终都是实数表达形式，电力线路的电压相量图如图2所示。

图2 电压相量

若已知某支路末端电压为U-，末端功率为S-=P+jQ，导线阻抗Z=R+jX，则该支路的电压损耗和功率损耗公式推导过程如下。

电压降低过程中的dU满足关系式：

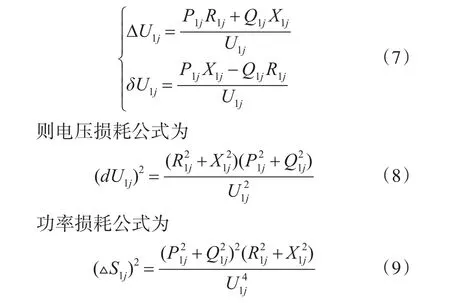
由电力系统稳态分析中关于电力线路上的电压损耗和功率损耗计算公式可知：

3.2 目标函数优化

3.3 能量优化约束条件

为了保证微电网正常运行，微电网中微电源应有以下约束条件：功率平衡条件、微电源出力约束、微电源出口电压约束。若Pij、Qij分别表示第i种微源的第 j个的输出有功功率和无功功率，PL、QL分别为负载所需的有功功率和无功功率，则微电网运行必须满足功率平衡约束为

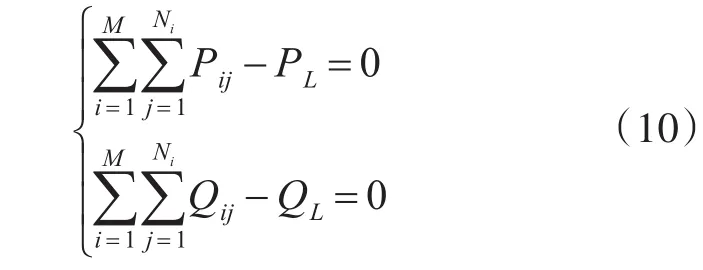
若Pijmin、Pijmax分别为第i种微源的第 j的输出有功功率最小值和最大值；Qijmin、Qijmax为第i种微源的第 j个输出的无功功率最小值和最大值。为了保证每个微电源的稳定运行，发电机的功率输出需要在一定的范围内：

微电源出口电压也应满足一定的约束条件，用Uij表示第i种微源的第 j个出口电压，Uijmin、Uijmax分别表示第i种微源的第 j个出口电压的最小、最大值。则应满足下面的约束条件：

4 实验算例

为计算简便，本例微电网结构包括2个20KW光伏电池（photovoltaic，PV）、2个30KW风力发电机（wind turbine，WT）和2个60KW微型燃气轮机（microturbine，MT），蓄电池组最大储存容量为10KW。优化目标是在约束条件限制下，各分布式电源有功和无功的值分别为多少时，可分别使得电压损耗和功率损耗达到最小。假定系统满足以下假设条件：

1）由于线路中电压降允许降落10%，为保证母线上电压为0.4KW，故令光伏发电机、风力发电机、柴油发电机出口电压均为UN=0.44KV；

2）DG为蓄电池，忽略此条线路上的电压损耗和功率损耗。为便于计算，将微电网结构图进行简化。

考虑到配电网辐射状的网络结构和低压线路参数的特点，取线路电阻 R=0.64Ω/km，X=0.1Ω/km，各发电机组线路长度与分布式电源负载的参数如表1所示。

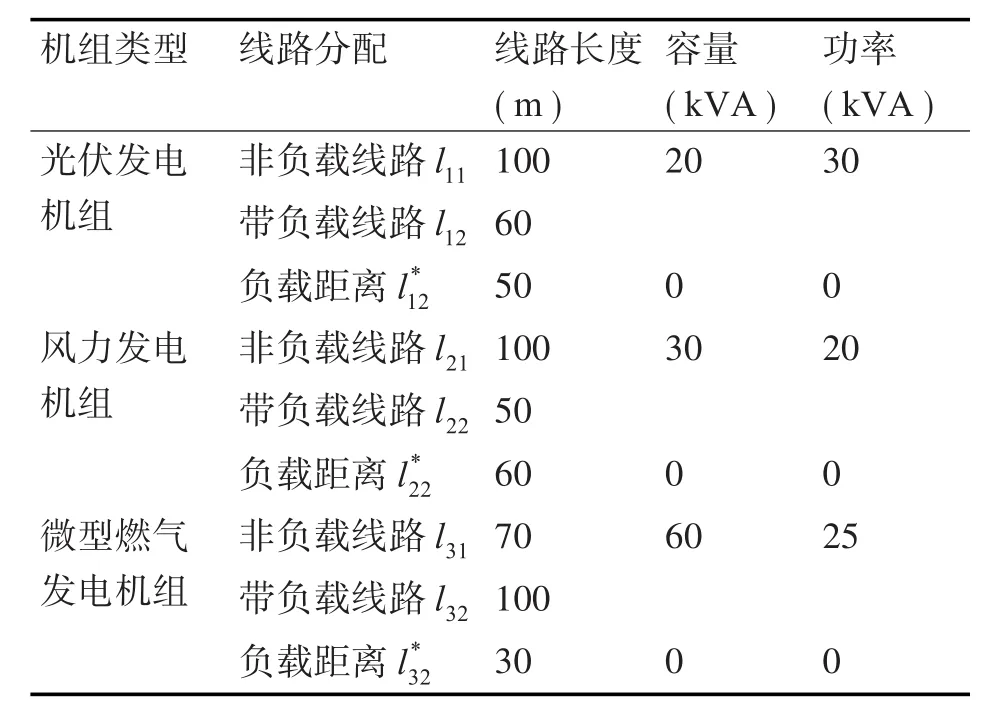
表1 线路长度与负载参数

则阻抗为

其中lij为第ij条线路的长度。则得到各支路阻抗为

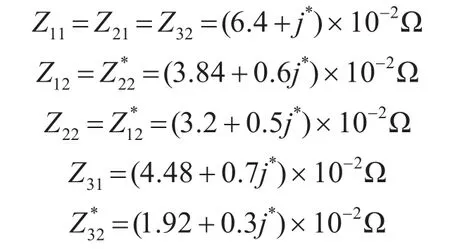
假设Pij、Qij是决策变量，则等式约束条件为

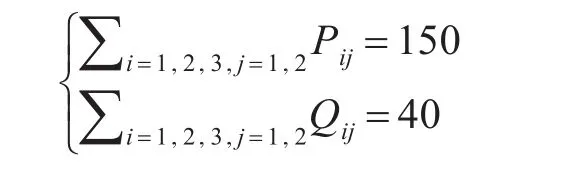
通过构造拉格朗日约束函数，求得储能蓄电池电压损耗最小值为

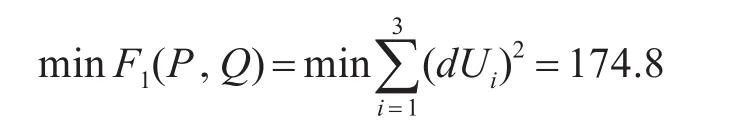
各机组发出的复功率使得储能蓄电池电压损耗的平方达到最小值，即13.2V。同样使用构造拉格朗日约束函数，求得储能蓄电池功率损耗最小值为

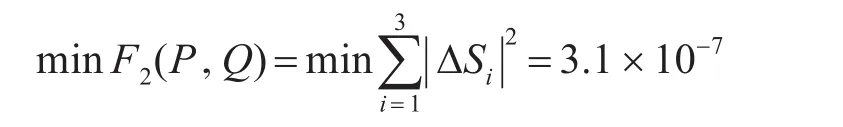
此时，各机组发出的复功率使得储能蓄电池功率损耗的平方达到最小值，即5571VA。经验证驻点处的函数值，具体的线路复功率如表2所示。

表2 不同最小损耗条件下的线路复功率

5 结语

本研究以微电网中分布式电源并网过程中电源的电压损耗和功率损耗最小为出发点，通过搭建光伏发电系统、风力发电系统、微型燃气轮机和储能蓄电池组的微电网结构。先构造微电网目标函数，然后建立微电网运行约束条件，最后达到对微电网电源能量进行优化。研究过程中，将各发电机组线路分为是否带负载进行区别，利用线路在电能传输过程中的阻抗推导出电压降低带来的电能损耗。在求解过程中，采用拉格朗日约束法对搭建的目标函数进行求解，使得最终的结果更加精确。

［1］杨新法，苏剑，吕志鹏.微电网技术综述［J］.中国电机工程学报，2014（1）：57-70.

YANG Xinfa，SU Jian，LV Zhipeng.Review of Microgrid Technology［J］.Transactions of China Electrotechnical So⁃ciety，2014（1）：57-70.

［2］王成山，武震，李鹏.微电网关键技术研究［J］.电工技术学报，2014（2）：1-12.

WANG Chengshan，WU Zhen，LI Peng.Research on Key Technologies of Microgrid［J］.Transactions of China Elec⁃trotechnical Society，2014（2）：1-12.

［3］武星，殷晓刚，宋昕.中国微电网技术研究及其应用现状［J］.高压电器，2013（9）：142-149.

WU Xing，YIN Xiaogang，SONG Xin.Research and appli⁃cation of microgrid technology in China［J］.High-voltage electrical appliances，2013（9）：142-149.

［4］苏阔，郭莉，李钦.光伏并网对地区电网线损的影响［J］.吉林电力，2015，43（5）：14-17.

SU Kuo，GUO Li，LI Qin.Influence of grid-connected PV on line loss of regional power［J］.Electric Power of Ji⁃lin，2015，43（5）：14-17.

［5］高曦莹，李广翱，扬爽.光伏电站并网对配电网线损率影响的研究［J］.沈阳工程学院学报（自然科学版），2013，9（3）：214-217.

GAO Yiying，LI Guanghan，YANG Shuang.Study on Influ⁃ence of Grid-connected PV System on Line Loss Rate of Distribution Network［J］.Journal of Shenyang Institute of Engineering（Natural Science Edition），2013，9（3）：214-217.

［6］杨洁.浅析并网风电场联络线线损［J］.计算机光盘软件与应用，2012（18）：146-147.

YANG Jie.Analysis on Line Loss of Connecting Line of Connected Wind Farm［J］.Computer CD-ROM Software and Application，2012（18）：146-147.

［7］于文鹏，刘东，翁嘉明.含分布式电源的配电网供电恢复模型及改进贪婪算法［J］.电力系统自动化，2013，37（24）：23-30.

YU Wenpeng，LIU Dong，WEN Jiaming.Distribution Pow⁃er Supply Restoration Model with Distributed Power and Improved Greedy Algorithm［J］.Automation of Electric Power Systems，2013，37（24）：23-30.

［8］雍静，徐欣，曾礼强.低压直流供电系统研究综述［J］.中国电机工程学报，2013，33（7）：42-52.

YONG Jing，XU Xin，ZENG Liqiang.Review of Low Volt⁃age DC Power Supply System［J］.Transactions of China Electrotechnical Society，2013，33（7）：42-52.

［9］曾鸣，马少寅，王蕾.基于分布式电源并网的配电网线损分摊定价模型［J］.华东电力，2011（12）：1965-1968.

ZENG Ming，MA Shaoyin，WANG Lei.Distribution net⁃work loss allocation pricing model based on distributed power supply［J］.East China Electric Power，2011（12）：1965-1968.

［10］谭兴国，王辉，张黎.微电网复合储能多目标优化配置方法及评价指标［J］.电力系统自动，2014，38（8）：7-14.

TAN Xingguo，WANG Hui，ZHANG Li.Multi-Objective Optimal Allocation Of Composite Energy Storage and Its Evaluation Indexes In Micro-Electric Power Systems［J］.Power System Automatic，2014，38（8）：7-14.

［11］李存斌，张建业，李鹏.考虑成本、排污及风险的微电网运营多目标优化模型［J］.中国电机工程学报，2015，35（5）：1051-1058.

LI Cunbing，ZHANG Jianye，LI Peng.Multiobjective Op⁃timization Model for Microgrid Operation Considering Cost，Discharge and Risk［J］.Transactions of China Electrotechnical Society，2015，35（5）：1051-1058.

［12］黄伟，黄婷，周欢.基于改进微分进化算法的微电网动态经济优化调度［J］.电力系统自动化，2014，38（9）：211-217.

HUANG Wei，HUANG Ting，ZHOU Huan.Dynamic Op⁃timal Dispatch of Microgrid Based on Improved Differen⁃tial Evolution Algorithm［J］.Automation of Electric Pow⁃er Systems，2014，38（9）：211-217.

［13］李文静，安工厂.基尔霍夫电压定律在电路分析中的应用［J］.电子科技，2013，26（7）：136-138.

LI Wenjing，AN Gongchang.Application of Kirchhoff's Voltage Law in Circuit Analysis［J］.Electronic Sci.&Tech，2013，26（7）：136-138.

［14］彭思敏，施刚，蔡旭.基于等效电路法的大容量蓄电池系统建模与仿真［J］.中国电机工程学报，2013，33（7）：11-18.

PENG Simin，SHI Gang，CAI Xu.Modeling and Simula⁃tion of Large Capacity Battery System Based on Equiva⁃lent Circuit Method［J］.Transactions of China Electro⁃technical Society，2013，33（7）：11-18.