空中爆炸冲击波对生物目标的超压-冲量准则*

王新颖，王树山，卢 熹，王建民

(1.北京理工大学爆炸科学与技术国家重点实验室,北京 100081;2.沈阳理工大学装备工程学院,辽宁 沈阳 110159;3.第三军医大学野战外科研究所,重庆 400042)

空气爆炸冲击波作为主要的毁伤因素，作用范围大，破坏力强，可以毁伤人员、设施和装备等各种军事目标以及民用建筑，一直以来都是被关注的重要问题。无论战争还是和平时期，爆炸冲击波均是生物致伤、致残甚至致死的重要因素[1-5]，例如在2015年8月12日天津港发生严重爆炸，爆炸造成的空气冲击波使数百人不同程度的受伤。

空中爆炸冲击波是一种具有较高幅值且持续微秒级至毫秒级时间的强间断压力波，其毁伤效果主要取决于两个相关的物理参数：峰值超压和正压作用时间。对于短时间的脉冲毁伤主要是依赖于峰值超压，而对于长时间的脉冲毁伤主要依赖于正压作用时间，即比冲量，峰值超压和比冲量相互影响且相互关联。常用的爆炸冲击波毁伤准则有超压准则、比冲量准则和超压-冲量准则，其中超压-冲量准则因考虑全面和评价准确等优点而得到广泛应用[6-7]。超压-冲量准则通常以超压-冲量曲线的形式给出毁伤预测，许多中外学者对超压-冲量曲线进行了一定的数值计算和理论研究[8-12]，但对生物目标的超压-冲量准则较少。本文中基于爆炸相似律，建立一种包括炸药药量和爆炸距离的归一化毁伤准则形式，通过参数取值来表示不同的毁伤判据；并以羊作为生物目标研究了冲击波对其毁伤，得到了超压-冲量曲线，通过曲线拟合得到了超压-冲量准则的表达式。

1 冲击波毁伤实验

1.1 实验方案

为获得空中爆炸冲击波对生物目标的毁伤准则与判据，进行TNT炸药不同药量的裸装药空中爆炸毁伤效应实验研究，实验示意图如图1所示。TNT装药制成等长径比圆柱形装药，装药密度为1.60 g/cm3，药量分别为0.25、1.00、4.00和8.00 kg。将TNT放置在距离地面1.5 m高的支架上，通过理论和数值计算确定3个相同比距离处，即等超压点(0.5、0.25和0.05 MPa)距爆心的水平位置，见表1所示，在这3个点的地面放着传感器测量冲击波压力，为了消除实验误差，每个点放置3个传感器；实验选取山羊共28只，体重约30 kg，每发实验在3个点位置进行布放，0.5和0.05 MPa的超压点放置2只，0.25 MPa超压点放置3只，实验羊均以右腹面向爆点，立姿站立固定在活动支架内，互相不遮挡；实验前对实验用羊进行编号体检，实验后对实验羊进行大体与病理解剖、脑电、心电、生化检测分析等检查，评估冲击波对实验羊的毁伤情况。

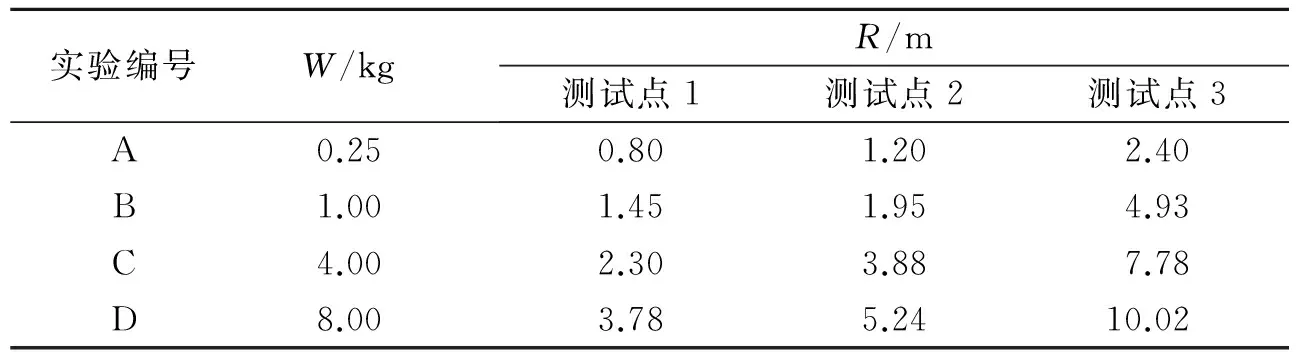
表1 3个等超压点距爆心的水平位置Table 1 Horizontal distance between three test points and burst point

1.2 冲击波测试实验结果

实验采用带有壁面压力传感器的自存储式数字压力记录仪，数字压力记录仪放入专用埋设罐体，安装在预先挖好的坑内，数字压力记录仪的工作表面、埋设罐体的上表面和地表面应当设置在同一平面上，以防止冲击波掠过传感器的工作表面时产生不规则绕流的影响。压力传感器将爆炸后产生的冲击波压力信号转换成电信号，通过信号调试仪输入数据采集仪，由压力传感器的灵敏度和信号传输、记录系统的放大倍数，得到空气冲击波在地面上的扫射压力或反射压力时程(冲击波反射超压-时间曲线)。

对实验进行冲击波压力测量，处理数据后得到冲击波参数随药量和距离变化曲线如图2所示。

图2(a)和(b)分别为冲击波入射超压随被试炸药质量和测试点水平距离的关系，每发实验的3个等比距离的测试点布放，从图2(a)中也可以看出实验数据和计算值较为接近，这说明理想炸药符合爆炸相似律，实验中通过计算得到的测试点位置相对准确，0.25 kg TNT可能受到支架影响，实验值偏低；从图2(b)中可以看出冲击波超压随药量的增大，冲击波压力衰减变慢。图2(c)、(d)是冲击波比冲量随被试炸药质量和测试点水平距离的关系，可以看出，在超压点接近相同时，比冲量随着药量的增加而增大；相同药量时，比冲量随距离衰减接近直线，衰减幅值受药量影响较小。

1.3 羊毁伤实验结果

爆炸冲击波对生物目标的损失主要体现在肺损伤，其次是心脏损伤和鼓膜损伤。本次实验中实验动物由第三军医大学野战外科研究所进行实验解剖，根据被试动物的损伤程度，主要依据损伤严重度判定以简明损伤计分法(abbreviated injury scale, AIS)，同时结合爆炸冲击波、冲击振动损伤与人员作业能力，制定了本损伤评估等级标准，以整体的动物损伤严重程度指数(severity of injury index, SII)为主要表征形式。毁伤等级与SII评分对应情况表2所示，Ⅰ级毁伤的生物为重伤至死，死亡概率约为90%，其SII评分为1.0～7.1；Ⅱ级毁伤对应为中到重伤，死亡概率为50%，其SII评分为0.3～1.9；Ⅲ级毁伤为轻伤或无伤，其SII评分为0.2～1.0。

实验后对实验羊进行综合解剖分析，得出SII综合损伤评分后，根据上述定义，对每发实验各测试点确定出毁伤等级如表2所示。从实验冲击波测试结果和实验羊的毁伤情况可以看出，在具有相同峰值超压的冲击波作用下，由于压力作用时间不同，采用大装药量会比小装药量造成羊的毁伤更严重；反之，相同比冲量下，由于压力幅值的不同，药量越大，超压越小，羊的毁伤程度越小；由此可见，单一的冲击波特征参量不能与目标的毁伤程度一一对应，应用超压-冲量准则评价冲击波对羊的毁伤比较合理。

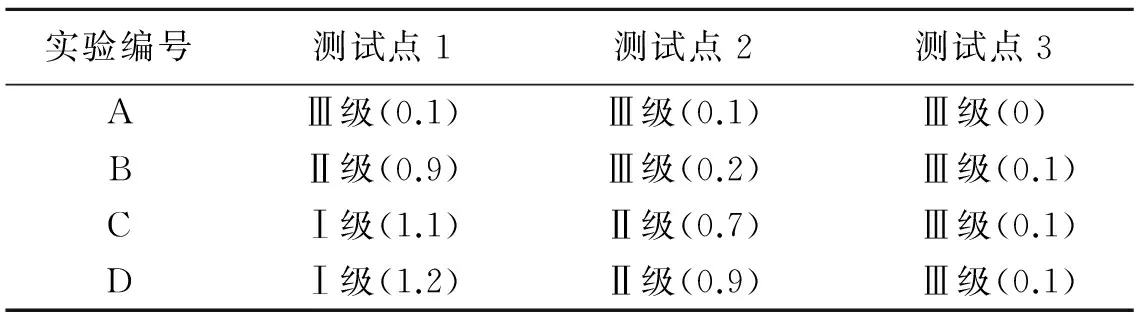
表2 各测试点羊的毁伤等级(SII评分)Table 2 Damage levels of tested samples at each test point

2 超压-冲量毁伤准则的建立

通过实验得到了不同药量和不同距离处的生物目标对应的毁伤等级，但这些实验数据点是离散的，为了获得一条连续性的超压-冲量曲线，从理论分析得到连续性的毁伤准则形式，通过离散的实验数据点确定出毁伤判据形式。

2.1 归一化冲击波毁伤准则

常用来描述空中爆炸冲击波威力的特征参量包括峰值超压pm和比冲量i[13]，这2个特征参量并不独立，每个特征参量仅表征冲击波某一方面的威力特性，而目标毁伤是冲击波载荷综合作用的结果。

根据爆炸相似理论，对于TNT装药，各参量在工程上的经验计算式为[13]:

(1)

(2)

式中：W是炸药质量，kg；R是距爆心的距离，m。由上两式可知，冲击波特征参量都可以表示为装药量W和爆距R的幂数形式，记为：

(3)

当CX的取值相等，则对应的冲击波特征参量相等。因此，若存在一种毁伤准则形式，其取值在任意药量范围都应与目标毁伤程度保持一一对应关系，那么该形式也应该满足式(3)，此时，α的取值决定了毁伤准则的具体形式。由前面讨论可知，α取值决定了冲击波特征参量的类型，对于TNT炸药空中爆炸冲击波，当α=1/3时，式(3)对应超压准则；当α=2/3，式(3)对应为比冲量准则；当α值应介于1/3～2/3之间，则式(3)就是超压-冲量准则。

2.2 毁伤判据的确定方法

在理想情况下，每个毁伤等级下对应一个毁伤判据，毁伤准则的取值应与目标毁伤程度存在一一对应关系。假设一组药量为W0、爆距为R0的空中爆炸条件造成目标某一等级的毁伤，由式(3)可得到超压准则和比冲量准则分别为：

(4)

与该条件产生相同峰值超压和比冲量的药量W和爆距R关系满足：

(5)

为了计算方便，将上式转换为对数形式分别为：

(6)

若以lgW为横坐标，lgR为纵坐标建立坐标系，如图3所示，则式(6)为该坐标系下的两条过点(lgW0, lgR0)的等值线，如图3中直线Cp0和直线Ci0所示。图中峰值超压等值线Cp0和比冲量等值线Ci0具有不同的斜率，分别对应为超压准则和比冲量准则时的α取值。当等值线向下平行移动，相应的威力参量增大；当等值线向上平行移动，相应威力参量减小。采用超压-冲量准则时，存在一条临界等毁伤曲线(图3中直线CX0)，在峰值超压和比冲量等值线之间，在该曲线对应目标造成同等程度的毁伤。CX0线下方阴影部分区域都将对目标造成更严重的毁伤。令该临界等值线对应的准则形式为：

(7)

则CX=CX0就是(W0,R0)所对应毁伤等级下的毁伤判据，只要已知2个具有相同毁伤等级的目标毁伤离散点，就可以确定出临界毁伤等值线CX0。

3 冲击波对生物目标的超压-冲量毁伤准则

为了获得TNT炸药空中爆炸冲击波对生物目标的超压-冲量毁伤准则，先根据表2的4个实验条件下测试点处实验羊的毁伤等级，各位置对应的生物目标由实验序号(A～D)和测试点(1～3)具体表示，分别对应的离散点(lgW, lgR)绘制在对数坐标系中，如图4所示。然后将相同毁伤等级的离散点确定出对应的3条临界毁伤等值线CX0，再由式(7)对3条临界毁伤等值线进行拟合，分别得到对应Ⅰ、Ⅱ、Ⅲ级的毁伤判据形式如下所示:

从拟合得到的毁伤判据形式可以看出，所得的Ⅲ级毁伤所对应的α值为0.66，很接近冲量准则的α=2/3，可以判断对于生物目标，其毁伤等级越小，对应的α值越大。

利用获得的空中爆炸冲击波对生物目标的毁伤准则与判据，计算出不同毁伤等级下对应的峰值超压和比冲量，给出Ⅰ级和Ⅱ级毁伤的峰值超压与比冲量阈值随装药量的变化规律，如图5所示。Ⅲ级毁伤的规律相同，但由于数值较小，没有绘制在此图中。

图5中可以看出，峰值超压阈值随着药量的增加而减小，比冲量阈值随着药量的增加而增大；峰值超压和比冲量阈值变化的幅度均随着药量的减小而增大，其中峰值超压阈值在小药量范围的变化幅度最大。图中规律表明：峰值超压或比冲量准则得到的毁伤判据在不同药量范围不具有一般性；装药量越小，由毁伤判据确定的战斗部威力范围与实际的偏差越大。由此可见，2种准则形式单一的判断冲击波对生物目标的毁伤不适合，而超压-比冲量准则综合考虑可两者的毁伤作用，适合作为冲击波对生物目标的毁伤判断标准。

4 结 论

(1)基于爆炸相似律，提出以药量和爆距表征的归一化的毁伤准则表达式，对应不同的指数取值有不同的毁伤准则形式；

(2)进行不同的参数的生物毁伤效应实验，确定出毁伤等级，对应实验数据；由实验数据确定出超压-冲量准则对应的指数取值，将离散的数据点转换为连续性的超压-冲量曲线，并拟合得到了超压-冲量破坏准则模型。

[1] GRUSS E. A correction for primary blast injury criteria [J]. Journal of Trauma, 2006,60(6):1284-1289.

[2] MACFADDEN L N, CHAN P C, HO K H, et al. A model for predicting primary blast lung injury[J]. Journal of Trauma & Acute Care Surgery, 2012,73(5):1121-1129.

[3] GIBBONS M M, DANG X, ADKINS M, et al. Finite element modeling of blast lung injury in sheep[J]. Journal of Biomechanical Engineering, 2015,137(4):1-9.

[4] FAN J Q, YANG J X, KONG F L, et al. A theoretical model on blast lung injury from an explosion[J]. Advanced Materials Research. 2014,850:1220-1224.

[5] 周杰,陶钢.人体胸部爆炸冲击波创伤模型与评估[J].弹道学报,2013,25(3):64-69.

ZHOU Jie, TAO Gang. Injury model and assessment for human thorax under blast wave[J]. Journal of Ballistics, 2013,25(3):64-69.

[6] 王芳,冯顺山,俞为民.超压-冲量毁伤准则及其等毁伤曲线研究[J].弹箭与制导学报,2003,23(2):126-130.

WANG Fang, FENG Shunshan, YU Weimin. Research on over-pressure impulse criteria and its iso-damage curve[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2003,23(2):126-130.

[7] 冯顺山,王芳,胡浩江.爆炸冲击波防护效应的评价方法研究[J].安全与环境学报,2004,4(增刊):173-176.

FENG Shunshan, WANG Fang, HU Haojiang. Study on evaluation method of explosion shock wave protection effect[J]. Journal of Safety and Environment, 2004,4(suppl):173-176.

[8] 陈赟,冯顺山,王芳,等.爆炸冲击波作用下的金属板损伤P-I图仿真[J].科技导报,2010,28(18):52-56.

CHEN Yun, FENG Shunshan, WANG Fang, et al. Numerical methods of pressure-impulse diagrams for damages of plates under blast loads[J]. Science & Technology Review, 2010,28(18):52-56.

[9] SHI Y C, HAO H, LI Z X. Numerical derivation of pressure-impulse diagrams for prediction of RC column damage to blast loads[J]. International Journal of Impact Engineering, 2008,35(11):1213-1227.

[10] DRAGOS J, WU C Q, HASKETT M, et al. Derivation of normalized pressure impulse curves for flexural ultra high performance concrete slabs[J]. Journal of Structural Engineering, 2013,139(6):875-885.

[11] DRAGOS J, WU C Q. A new general approach to derive normalized pressure impulse curves[J]. International Journal of Impact Engineering, 2013,62:1-12.

[12] SYED Z I, LIEW M S, HASAN M H, et al. Single degree of freedom based pressure-impulse diagrams for blast damage assessment[J]. Applied Mechanics and Materials, 2014(567):499-504.

[13] 隋树元,王树山.终点效应学[M].北京:国防工业出版社,2000.