情境创设之我见—教学案例:《勾股定理》复习课实录
2018-03-20沈菊萍
沈菊萍
(江苏省张家港市锦丰初级中学,江苏张家港 215624)
引 言
创设教学情境指教师有意识地应用情感、艺术、兴趣等因素来调动、启发学生的无意识心理活动,以调动学生有意识的心理活动及行为,最大限度地挖掘学生的生理和心理潜能,激发学生的学习兴趣,拓展学生思维空间,使学生积极主动地投入课堂学习中[1]。
许多学生不喜欢上数学复习课,认为复习课枯燥乏味,但是要掌握数学知识、提高数学能力,巩固与反馈必不可少。因此,笔者常常用情境教学法进行复习课教学,学生的兴趣有了很大的提高,复习效果也显著提升。笔者就以《勾股定理》复习为例,谈谈关于数学复习课的心得体会。
一、课前导入练习
设计意图:第一题复习了勾股定理,让学生通过动手作图,得到图形的特征,根据已知条件建立形与式的关系,同时也复习巩固了直角三角形的边之间的特殊数量关系式。第二题考查勾股定理的逆定理,通过对比,得到两个定理之间的互逆关系,复习了两者之间的区别与联系。
学生活动:在课前准备中,教师可以让两个学生(相对基础薄弱的学生)为代表,在黑板上板书,上课后请他们分析问题的方法,树立他们学好数学的自信心,使他们能带着愉快心情进入课堂教学。
【例题1】在Rt△ABC中,∠C=90°,BC=5,AC=12。
1. AB=________________ ;
2.若E点为AB的中点,则CE=___________ ;
3.若CD⊥AB,则高CD=______________ 。
二、教学过程
(一)故事化地引入课堂
选择恰当的复习课例题是唤醒学生记忆的关键。通过哪个问题引入,提炼数学思想,达到知识系统化、条理化至关重要[2]。
【例题3】有一个圆柱,它的高是12厘米,底面周长是18厘米,如图1,在圆柱下底面上的A点有一只蚂蚁,若想从点A爬到点B,蚂蚁沿着圆柱侧面爬行的最短路程是多少?
设计意图:这是一道与生活息息相关的题目,很快吸引了学生的注意力。简单地提问激发学生已学过的平面图形与立体图形间的冲突,使学生们很快融入问题情境中,开始思考数学问题。化曲为直的方法是解决这类题型的关键,它引导学生将立体图形转化为平面图形,并找到平面图形中的特殊平面图形直角三角形。学生应用勾股定理就可直接解题。这类与生活相关的题目可以让学生找到数学的意义,让学生明白数学知识与生活紧密联系,可以解决生活中的问题。
学生活动:学生独立思考后,教师可请学生代表发言,如有不足之处,再请学生补充。
教师活动:教师在学生回答问题时认真倾听,并适时进行点拨。

图1
(二)生活化地导入例题
【例题4】如图2,受台风“山竹”影响,一棵8米高的大树在离地面某处断裂,树的顶部落在离树根底部前方3米处,问折断处离地面有多高?(注:树干与地面垂直)
设计意图:与例题3相比,这道题更具生活化。学生们经常看到有关台风的消息,对台风带来的破坏性更是比较熟悉。题中提供的数字问题相对的简单,能让学生产生攻克它的信心。此题的主要意图是建立应用勾股定理的数学模型以及方程思想的应用,让学生能在这两个思想方法的引领下熟练地用勾股定理解决问题。
学生活动:学生先独立思考探索,然后在学习小组内交流,合作寻找解题方法,独立完成解题过程,再进行小组间交流,由小组代表展示解题思路。
教师活动:整个过程中,教师应努力引领学生自主思考,走进小组内与学生一起活动,给予有效的引导。此处方程的解答过程,教师可以考虑让后进生进行黑板板书,使他们参与课堂教学。在学生展示的过程中,教师应充分发挥例题的示范性功能,培养学生的解题格式和规范。

图2
(三)探究化地提升
【变式1】如图3,在矩形ABCD中,将矩形沿BD折叠,点A落在A′处。
1.判断BF与DF的关系并说明理由;
2.若 BC=8,CD=4,求重叠部分△BFD的面积。
设计意图:翻折问题是轴对称平行四边形中的常见问题。通过翻折,图形中会出现熟悉的轴对称图形——等腰三角形,同时出现另一种特殊的三角形——直角三角形,这就出现了例题4中的图形,此时新知与旧知之间产生联系,能够培养学生举一反三、触类旁通的能力。
学生活动:学生独立思考,然后以小组为单位,以生教生,教师批改小组长的解答过程,小组长批改组员的解答过程,教师使用多媒体展示优秀作业。
教师活动:在学生中巡视,参与到学生活动中,注意关心后进生在图形上做出的数据标注,引导他们应用勾股定理建立方程。
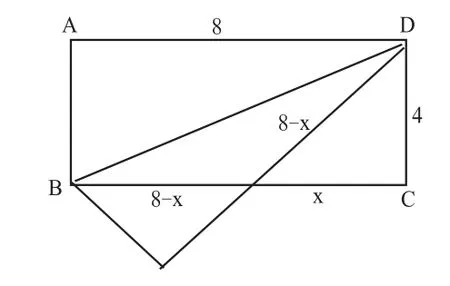
图3
(四)参与化发展与巩固
【变式2】如图4,已知在△ABC中,∠A=75°,∠B=60°,AC=8,求BC长。
设计意图:这道题考查了另一种数学思维,此题中没有出现直角三角形,也没有上述例题中的数学模型存在,它的主要目的是引导学生们构建直角三角形,再应用勾股定理解题。做高线是构建直角三角形的常用方法。
学生活动:学生很快进入自觉讨论的学习状态中。
教师活动:引导学生考虑题目中的两个问题:1.没有特殊的三角形,所以边长的提供是否没有用武之地?2.特殊角75°一般如何分割?
学生活动:学生互相讨论,并动手操作构建图形或者分解图形。
教师活动:对学生讨论的高线的引入方法提出疑问及肯定、表扬,保护学生的自尊心和学习热情。

图4
三、课堂小结
经历上述例题讲解后,一节复习课就进入尾声,教师可将课堂小结时间交给学生,并提出明确要求。
1.小组成员先从习题内容、数学思想方法、获取知识的途径进行总结,后由“发言人”汇报。
2.小组间展开竞争,选出表现最佳的小组。
3.教师用多媒体展示本课中的重要数学方法与思想方法,与学生的总结进行对比。
四、课后反思
(1)抽象问题故事化、数学问题生活化。教师注重问题情境的设计,贴切学生的生活实际,打开学生思维的空间,再通过教师点拨回到问题的中心,这种独特的构思设计有利于提高学生转化抽象问题的能力。
(2)传授知识系统化,重视学生的探究、参与,提炼数学思想。教师在讲课时应注重深入浅出,问题设计要具有层次性,环环相扣,通过让学生进行比较、选择,再配以文字结论与图像,最后回归到简单的模型中。这样可以在不知不觉中渗透数学建模思想、转化思想、数形结合思想和分类思想,让学生“在练中学、在学中悟”,逐步掌握数学思想方法。
(2)规范化的数学教学,注重学生演绎推理能力的发展。教师在上课时应注意言谈举止,注意语言的精炼。教师的眼神、语态都能直接影响学生的思维,因此,教师对学生的鼓励、激励、奖励要相间而行,板书要设计合理,凡有价值的字迹都应留在黑板上。例题解题过程的书写要规范,要引导学生在自主思考、讨论和分析下解决问题,而教师只需适当启发、提醒。
(4)这节复习课根据学生的前期学习情况制定复习目标,确定复习内容。教师通过几个小题带领学生复习概念,构建章节知识网络。本节课中的例题设计既能够兼顾基础,又能够提升学生思维能力。教师应通过问题引导方法,提炼数学思想,实现知识系统化、条理化。同时,教师要注意发挥学生的主动性,推动学生独立思考,提高对知识的梳理能力。
(5)在复习的同时,教师要注意对后进生的学习信心给予保护与鼓励。
结 语
复习课的教学过程要清楚,环节紧凑、流畅,由易到难,层次分明;知识的梳理要清晰,既要对整个章节进行整理、概括,让学生从整体、系统的角度对知识进行回顾,又要有创新、独到之处,培养学生的基本数学思想。复习课中教师可将整个教学过程变成学生自己探索提升的过程,从而提高学生能力。同时,教师在设计复习课题目时,要兼顾基础,体现能力。可针对前一课中多发的错题进行编拟,要以小见大。
