旋转纹理不变模型下的快速人脸匹配方法

向世涛，文 畅，谢 凯，贺建飚，刘从浩

(1.长江大学 电子信息学院，湖北 荆州 434023；2.长江大学 计算机科学学院，湖北 荆州 434023；3.中南大学 信息科学与工程学院，湖南 长沙 410083)

0 引 言

由David Lowe提出的SIFT(scale-invariant feature transform)模型[1,2]成为目前人脸特征匹配技术应用最广泛的模型之一。虽然SIFT模型对于人脸匹配鲁棒性较高，但还存在许多需要改进的地方，相关问题引起国内外学者关注。Seba Susan等[3]提出将模糊匹配系数应用到SIFT模型中，形成高效的模糊筛选描述符；Sohee Park等[4]采用Gabor-LBP直0方图和SIFT-based特征点结合的方法；Gautam Narang等[5]提出基于SIFT和LMBP神经网络分类的面部识别方法。

上述学者都有效地优化了SIFT模型在人识别中的应用，但传统的SIFT模型仍存在当图像有多个相似区域时，容易造成误匹配的情况。为此，提出一种RISIFTTF模型下的快速人脸特征匹配方法，将具有旋转纹理不变性的RITF特征向量与SIFT特征向量融合，形成特征有RISIFTTF描述向量，从而有效地提高了特征匹配的效率。而且利用GPU强大的并行计算能力，优化了方法的计算时间，使其更加高效精确。

1 RISIFTTF模型

传统的SIFT模型是一种提取图像局部特征的模型，它在匹配过程中，仅使用图像的局部特征描述符进行匹配，难免会由于缺少纹理、目标过小等原因而造成误匹配。即使能够消除部分的误匹配点对，但由于局部特征的相似性，而导致剔除这些误匹配点对的能力有限[6,7]。当人脸图像中存在多个相似的纹理信息区域时，只有关键点周围图像区域的旋转不变性纹理特征等其它特征才能达到良好的效果。因此，本文提出了具有良好旋转纹理特征不变性的RISIFTTF模型。它分为4个步骤[8-11]：尺度空间极值检测、关键点定位、方向确定以及构建RISIFTTF描述符。流程如图1所示。

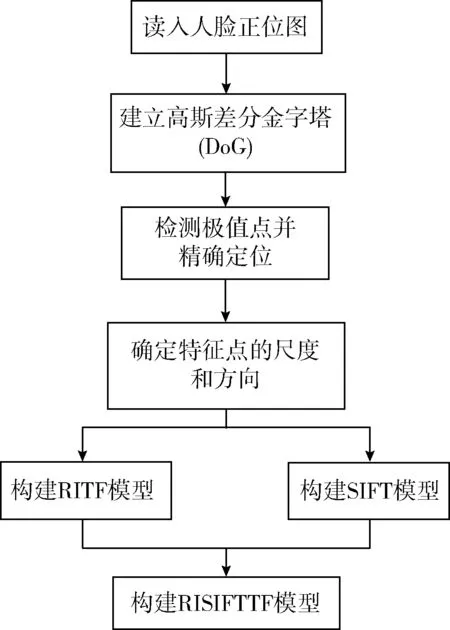
图1 RISIFTTF模型流程

1.1 尺度空间极值检测

建立高斯金字塔以及高斯差分金字塔(DoG)，并检测空间极值点。在高斯金字塔构建过程中，先将图像扩大一倍，在此基础上，对该尺寸下图像进行高斯模糊，几幅模糊之后的图像集合构成了一个八度。然后对该八度下的最模糊图像进行下采样操作，长和宽分别缩短一倍，图像面积变为原来1/4。该图像就是下一个八度的初始图像，在此基础上完成属于这个八度的高斯模糊处理，并以此类推完成的所有八度构建，从而形成高斯金字塔。再对同一个八度的两幅相邻图像相减得到差值图像，所有八度的这些差值图像的集合，就构成了高斯差分金字塔

D(x,y,σ)=[G(x,y,kσ)-G(x,y,σ)]⊗I(x,y)
=L(x,y,kσ)-L(x,y,σ)

(1)

式中：k——不同高斯核尺度，k的初值为1，尺度以k倍递增。

高斯差分金字塔的建立如图2所示。

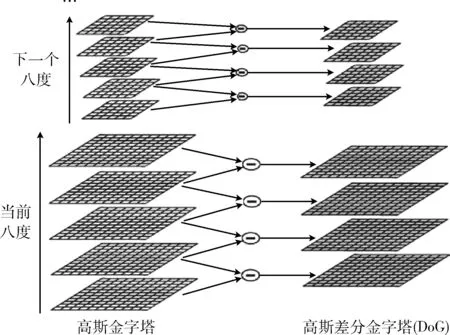
图2 高斯差分金字塔的建立

接下来便是在三维空间(图像二维，尺度一维)中，遍历检测极值点。具体过程是比较当前特征点的灰度值和其它26个点(当前尺度下该点相邻的8个点以及前后尺度下与该点最近的9个点)的灰度值大小。

1.2 关键点定位

由于图像是一个离散的空间，特征点的位置坐标都是整数，但在尺度空间中检测出来的关键点的坐标并不一定是整数。为了精确定位关键点的坐标，采用三元二次函数的泰勒公式，通过5次迭代确定极值点的位置

(2)

该公式是用已知的A点去估计附近B点的值。其中x=(x,y,σ)T是B点相对于A点的偏移。求上式极值，再对其求导，并令其导数为0，得

(3)

其中，若x0中有一维大于0.5，表明该点更接近另一点C，此时将其更新为C点，并且继续迭代过程；否则迭代结束，将x0追加到当前整数坐标，从而得到特征点的精确坐标。将上式求出来的x0代入原式，得

(4)

式中：当D(x0)≤0.03[2]时，判定该点为对比度较低的特征点。由于低对比度的点易受到噪声影响而变得不稳定，故去除这些低对比度特征点。

在精确定位后的特征点中还有一些边缘点，由于其对一些噪声不稳定，因此也需要在此去除。其特征是在垂直边缘的方向上的主曲率较大，在与边缘相切的方向上其主曲率较小，根据这些特征便可去除边缘点。主曲率通过2阶Hessian矩阵获得

(5)

其中，Dxx、Dxy、Dyy都可以通过当前的像素点与周围像素点相减得到。

由于某点的Hessian矩阵的特征值与该点的主曲率成比例的，因此可通过计算Hessian矩阵的特征值来确定该点的主曲率。设矩阵特征值分别为α和β(假设α>β)，则有

Tr(H)=Dxx+Dxy=α+β

(6)

Det(H)=DxxDyy-(Dxy)2=αβ

(7)

其中，Det(H)为矩阵的行列式，Tr(H)为矩阵的迹。通过计算α/β来比较特征点的主曲率，将α/β≥10[2]的点剔除。

1.3 方向确定

对于在高斯差分金字塔中检测出来的关键点，采集其所在金字塔中领域窗口内像素的梯度和方向分布

l(x,y)={[F(x+1,y)-F(x-1,y)]2+
[F(x,y+1)-F(x,y-1)]2}1/2

(8)

(9)

其中，l(x,y)和ρ(x,y)分别为高斯差分金字塔中(x,y)处梯度的模值和方向。

1.4 构建RISIFTTF模型

传统的SIFT模型是先根据特征点的尺度选择金字塔中的图像，然后计算其领域范围内各点的梯度方向和幅值。每个特征点都是由4×4共16个子点组成，其中每个子点有8个方向的向量数据，由此生成4×4×8共128维的特征向量模型。最后为了避免光照影响，对特征向量的长度做归一化处理。

接着是RITF模型的构建，以特征点为中心，图像最长对角线D为直径建立一个圆形区域，以此作为特征点的领域。将该领域等分为若干个同心圆领域，在省去高斯模糊和领域角度归零操作的情况下，依然保持良好的旋转不变性，同时还避免了图像旋转的运算代价。

(10)

(11)

其中，(xi,yi)和(xc,yc)分别为像素点Ii(x,y)和中心点Ic(x,y)在待描述区域的坐标，β为常数。接着把计算得到的所有加权RITF特征值组成一个一维特征向量，记为Ri，则有

Ri=[λ1*ritf1λ2*ritf2…λ64*ritf64]

(12)

现定义RISIFTTF模型如下

(13)

其中，S为128维的SIFT模型，R为64维的RITF模型，T为192维的RISIFTTF模型，α为相对权重因子，根据图像像素大小与类型而定，其中α≤1。

2 RISIFTTF模型的并行优化

2.1 GPU及CUDA架构

2007年NVIDIA公司发布用于GPU编程的官方开发平台CUDA[12](compute unified device architecture)，其核心思想是3个重要的抽象概念：共享存储器、线程组层次结构和屏蔽同步。

GPU可用于解决数据并行计算的问题——使许多数据元素在其上可被并行执行，具有较高的计算密度[13]。CUDA编程模型公开了GPU的并行能力，正是凭借于GPU独特的硬件架构设计，使其具有强大的并行数据运算能力(其大量的晶体管都是用于算术逻辑运算)。由于大量的数据元素在线程上独立运行，且具有较高的计算密度，因此并不需要较大的数据缓存。

2.2 GPU执行细节

本文将从以下几个方面来介绍RISIFTTF模型的优化与加速，其流程如图3所示，虚线左边表示程序在CPU端运行，右边表示在CPU端运行。

图3 RISIFTTF模型并行计算流程

2.2.1 高斯差分金字塔的建立及极值检测

在建立高斯金字塔时，由于每一层图像都需要进行高斯滤波运算，耗时太多，故采用二维卷积来计算。根据其可分性，分成行和列两个维度分别使用一维卷积核函数并行计算

I列(x,y)=I(x,y)*gx(t)

(14)

I行(x,y)=I列(x,y)*gy(t)=I(x,y)*gx,y(t)

(15)

由于列卷积与行卷积相似，故下面以列卷积运算为例对高斯金字塔的并行建立进行详细介绍。将block设置为二维，thread为一维。每次计算block读取部分图像数据并存放到shared memory，这样线程之间的数据通信能加快程序的并行计算。完成高斯金字塔的建立后，直接将相邻尺度的图像上的像素点相减便得到了高斯差分金字塔。由于相减时，不相邻的图像不受计算的影响，因此可以放在GPU上并行处理。同理，也可以对高斯差分金字塔中每层图像的像素点并行检测极值点，找到潜在关键点。接着通过二值位图标记关键点的位置和尺度，插入到序列中并传到Host端。

2.2.2 直方图统计

本文以半径为15个像素点的圆形领域作为关键点描述符的领域信息。为弥补因没有仿射不变性而产生的特征点不稳定问题，本文先用高斯平滑对整个圆形领域的梯度幅值做加权处理，再对该领域进行区域划分，将2π做36等均分，每个区域对应于一个block。统计每个block中像素梯度的梯度信息就能获得该特征点的直方图，查找出直方图中最大组距(bin)的值就是该特征点的主方向。为了更进一步的优化计算，本文将数据导入到RGBA纹理存储器中，利用高级图形卡上的多目标渲染算法进行加速处理。最后，将计算的结果压缩到一维数组，并从Device端传回到Host端，在CPU上接着更新梯度方向并建立SIFT描述符。

2.2.3 RITF模型构建

由于一幅图像一般会有上百个特征点，且每个特征点的RITF特征计算都比较耗时，故本文将该步骤放在GPU上运行。先将特征点位置以及图像等数据从Host端复制到Device端，并保存到Global memory，再为每一个block分配一个特征点的RITF特征值计算。由于一个grid中最多可以允许65535×65535个block，其数量远大于特征点数，所以不用担心数据溢出的问题。由式(10)～式(12)可以知道，RITF特征值计算与加权系数计算之间互不影响，故设计不同的kernel函数分别在两个stream中并行调用，并将RITF特征值和加权系数保存在不同的数组中。为了保证两者的值相互对应，RITF特征值的计算顺序应与加权系数的计算顺序保持一致。最后，在构建RITF模型之前，要确保所有的计算都已执行完成。为此，在这些kernel函数中，除了返回计算结果外，还应返回计算状态信息。

2.2.4 RISIFTTF特征匹配

RISIFTTF模型是由128维的SIFT模型和64维的RITF模型组合构建而成的，包含了两种不同的图像信息，应采用不同的匹配策略。对于SIFT局部特征向量S仍采用欧氏距离作为其匹配策略

(16)

式中：Si,m、Sj,m——SIFT局部特征第i个特征点的第m维特征向量和第j个特征点的第m维特征向量(m≤128)。

对于RITF局部特征向量R采用χ2统计量作为匹配策略

(17)

式中：Ru,m、Rv,m——RITF局部特征第u个特征点的第m维特征向量和第v个特征点的第m维特征向量(m≤64)。

在进行特征匹配时，将人脸图像数据从Host端传到Device端，利用GPU并行计算。将每个特征点的RISIFTTF特征向量放入一个block的shared memory中，给每个block分配192个thread，前128个thread计算欧氏距离，后64个thread计算χ2统计量，这样让一个thread去处理一维的匹配信息。最后，通过调用__syncthreads()函数实现线程同步，只有192个thread计算完后，才能去执行后面的流程。

3 实验结果与分析

3.1 实验运行平台

硬件平台：CPU为英特尔的Core i5-4258U处理器，主频2.40 GHz，内存8 GB。GPU为GeForce GTX 960M，640颗CUDA核，显存带宽80.16 GB/s，核心频率1097 MHz。

软件平台：操作系统为Microsoft Windows 10，编译器平台为Visual Studio 2010，CUDA Toolkit 7.5，OpenCV 2.4.8。

3.2 实验步骤与数据记录

3.2.1 实验测量参数

记匹配正确的人脸数为Nr，匹配错误的人脸数为Nw，没有匹配出来的人脸数为Nf(通常在进行特征匹配实验时，会以m个匹配点对作为阈值，来判断是否匹配成功)，CPU顺序执行的时间为TCPU，GPU并行执行的时间为TGPU，加速比为S，配准率为Rm，查全率为Rr，则有

(18)

(19)

(20)

3.2.2 人脸匹配方法改进前后对比

本文实验所用的人脸样本库来自于FERET[14]提供的人脸库(每张人脸图片大小80×80)以及自采集人脸数据库(每张人脸图片大小180×250)，其中包括正位人脸，侧位人脸，倾斜的人脸图像等。传统SIFT模型下的人脸匹配方法只是对正位人脸、旋转(倾斜)角度较小的人脸匹配效果好，而对旋转(倾斜)角度相对较大的人脸图匹配效果不佳；本文提出的改进方法是将具有旋转纹理特征不变性的RITF模型与SIFT模型融合，在保持原有匹配效果的基础上，对旋转(倾斜)角度较大的人脸都有较好的匹配效果。本次实验，针对相同的人脸库，将改进的RISIFTTF模型下的人脸特征匹配方法与传统SIFT模型下匹配方法进行比较。实验数据均为进行10次实验后的平均值。

对于FERET人脸库而言，如图4和图5所示，SIFT模型有3个匹配对点，但实际上只有两个匹配点是正确的；改进后的RISIFTTF模型可以匹配10对特征点，并且有8个匹配对点是正确的。

图4 SIFT模型

图5 RISIFTTF模型

两种方法对FERET库的人脸匹配效果见表1，改进后的人脸匹配方法将配准率提高了9.78%-13.96%，查全率提高了7.23%-8.70%(由于FERET人脸库中特征点较少，这里设置的匹配点对阈值m=3)。

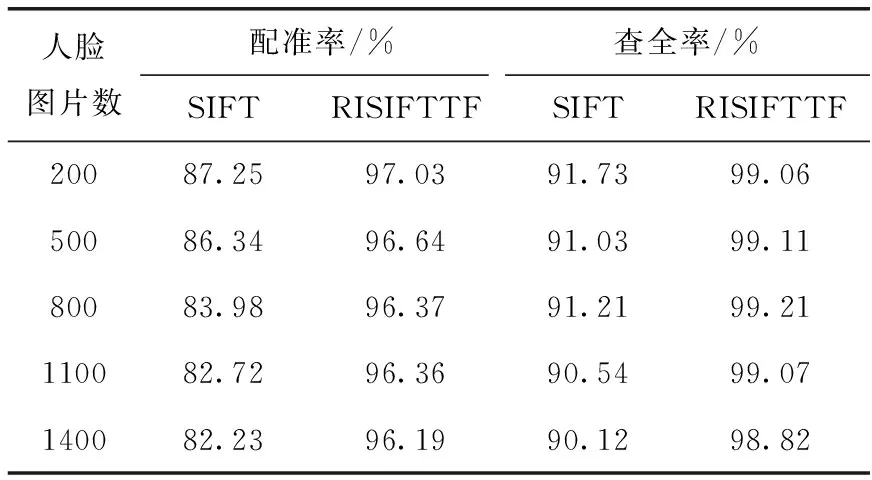
表1 FERET人脸库实验结果对比

对于自采集人脸库，如图6和图7所示，SIFT方法虽然有19个匹配对点，但实际上只有9个匹配点是正确的；改进后的RISIFTTF方法可以匹配31对特征点，并且有23个匹配对点是正确的。

图6 SIFT模型

图7 RISIFTTF模型

两种方法对自采集库的人脸匹配效果见表2，改进后的人脸匹配方法将配准率提高了10.53%-13.21%，查全率提高了6.95%-7.98%(匹配点对阈值m=16)。

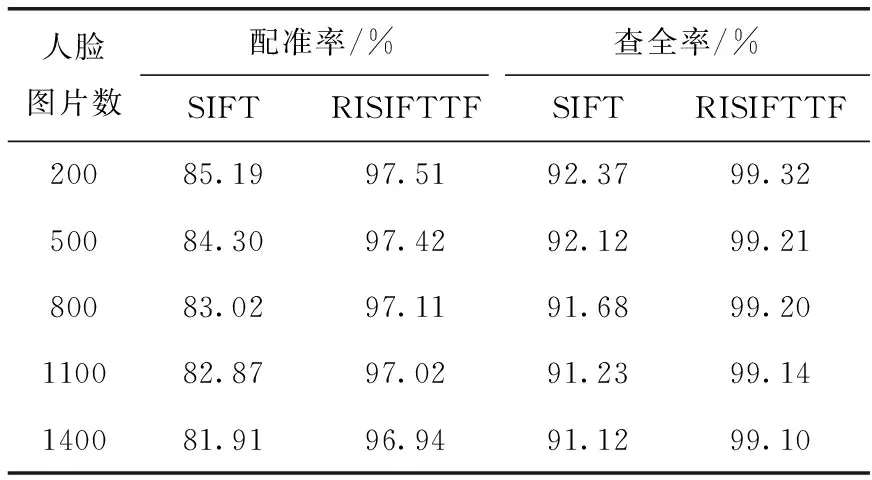
表2 自采集人脸库实验结果对比

图8为基于RISIFTTF模型的人脸检测与识别系统操作界面(为了较少软件的运行时间，这里使用灰度图进行匹配)。

图8 人脸检测与识别系统的操作界面

3.2.3 GPU优化前后对比

为了进行多组数据的对比实验，将FERET人脸库与自采集人脸库均根据图片数量的不同安排了5组实验。每组实验都是针对RISIFTTF模型将CPU串行计算与GPU并行计算进行对比，且每组实验测试的时间均是10次实验的平均值。

由表3可知，针对FERET人脸库，GPU并行计算对RISIFTTF模型的加速比可以达到5倍-6倍左右。

表3 CPU与GPU运算时间比较(FERET库)

由表4可知，针对自采集人脸库，GPU并行计算对RISIFTTF模型的加速比可以达到4倍-5倍左右。

表4 CPU与GPU运算时间比较(自采集库)

3.3 结论与分析

3.3.1 匹配性能分析

由上述实验可知，本文提出的RISIFTTF模型下的特征人脸匹配方法相较于传统方法具有很大的提升。对于FERET人脸库，人脸图片尺寸较小，均为灰度图像，虽然匹配点数较少，但优化效果还是比较好的，配准率依然可以提高到97.03%。对于自采集人脸库，人脸图片尺寸较大，均为彩色图像，因此匹配点对数较多，优化效果也更好，配准率高达97.51%。另外，改进后的方法明显地提高了匹配点对数，使得两个人脸库的查全率都能达到99%左右。

3.3.2 运算速度分析

由上述实验可知，利用GPU并行计算能有效的提高程序的运行速度，减少执行时间。相比于自采集人脸库，FERET人脸库中的人脸图片尺寸较小，且均为灰度图像，因此每幅图像的特征提取的计算时间较少，加速比较大，优化效果较明显。当图片数量不多时，并没有全面的利用到GPU上线程的资源，加速程度较小，加速比不是很高；但当图片数量逐渐增多后，GPU上所有线程都被调用起来，两个人脸库的加速比都逐渐提高。因此，GPU并行计算确实能够解决图片数量大的情况。

4 结束语

本文详细的介绍了一种RISIFTTF模型下的快速人脸匹配方法，并利用编程加以实现。该方法在保持原SIFT模型的优势的同时，结合RITF模型，提高了传统SIFT模型的旋转不变性，很好地改善了传统SIFT模型在图像存在多个相似区域时易造成误匹配的问题。并且本文利用GPU实现方法的并行加速，既保证了匹配精度，又能够有效提高运行效率，减少了运行时间。

但本方法的特征描述符的维数有192维，维数较多，不利于方法计算性能的进一步优化。下一步研究将会重点解决这方面的问题。另外，现如今云平台正逐渐成为热门领域，其带来的云计算相比单机的GPU并行计算更加的方便、高效。在解决维数问题的同时，进一步的研究将会尝试把优化方法放到云平台上，利用云计算去更有效地提高运行速度。

[1]Nilkanta Sahu,Arijit Sur.SIFT based video watermarking resistant to temporal scaling[J].Journal of Visual Communication and Image Representation,2017,45(5):77-86.

[2]Zhang Guixuan,Zeng Zhi,Zhang Shuwu.SIFT matching with CNN evidences for particular object retrieval[J].Neurocomputing,2017,238(5):399-409.

[3]Susan S,Jain A,Sharma A.Fuzzy match index for scale-invariant feature transform (SIFT) features with application to face recognition with weak supervision[J].IET Image Processing,2015,9(11):951-958.

[4]Park S,Yoo J H.Real-time face recognition with SIFT-based local feature points for mobile devices[C]//1st International Conference on Artificial Intelligence.New York:IEEE,2013:304-308.

[5]Narang G,Singh S,Narang A.Robust face recognition method based on SIFT features using Levenberg-Marquardt back propagation neural networks[C]//6th International Congress on Image and Signal Processing.New York:IEEE,2013:1000-1005.

[6]Jeahoon Choi,Seong Joon Yoo,Sung Wook Baik.Rotation invariant multiple face-detection architecture for smart TV[J].IERI Procedia,2014,6(4):33-38.

[7]Osós GC,Khoshgoftaar TM,Wald R.Rotation invariant face recognition survey[C]//Proceedings of the IEEE 15th International Conference on Information Reuse and Integration,2014:835-840.

[8]Bai Junfeng,Ma Yong,Li Jing.Good match exploration for thermal infrared face recognition based on YWF-SIFT with multi-scale fusion[J].Infrared Physics & Technology,2014,67(6):91-97.

[9]Vinay A,Dixit Hebbar,Vinay S Shekhar.Two novel detector-descriptor based approaches for face recognition using SIFT and SURF[J].Procedia Computer Science,2015,70(11):185-197.

[10]Vinay A,Ganesh Kathiresan,Durga Akhil Mundroy.Face recognition using filtered Eoh-sift[J].Procedia Computer Science,2016,79(4):543-552.

[11]CHANG Xujian,HAN Xie,XIONG Fengguang.Feature detection based on FAST detection and SIFT description[J].Computer Engineering & Design,2015,36(10):2749-2753(in Chinese).[常旭剑,韩燮,熊风光.基于FAST检测及SIFT描述的特征检测算法[J].计算机工程与设计,2015,36(10):2749-2753.]

[12]Devani U,Nikam V B,Meshram B B.Super-fast parallel Eigen face implementation on GPU for face recognition[C]//International Conference on Parallel.New York:IEEE,2014:130-136.

[13]CHEN Bin,CHEN Heping,LI Xiaohui.Efficient covariance matrix algorithm and realization for images on GPU[J].Computer Engineering & Design,2014,35(12):4238-4242(in Chinese).[陈彬,陈和平,李晓卉.基于GPU的高效图像协方差矩阵算法与实现[J].计算机工程与设计,2014,35(12):4238-4242.]

[14]Ladislav Lenc,Pavel Král.Automatic face recognition system based on the SIFT features[J].Computers & Electrical Engineering,2015,46(2):256-272.