基于权值向量矩阵约简的Apriori算法

杨秋翔，孙 涵

(中北大学 软件学院，山西 太原 030051)

0 引 言

数据挖掘是指通过数据分析，自动从大量数据中找出其中隐藏的特殊关系的过程[1]。关联规则挖掘作为使用最广泛的一种，可以发现大量数据间的关联关系，为人们快速决策提供依据。Apriori算法作为一种经典的关联规则挖掘算法，被广泛应用于商业和网络安全领域，但其存在数据库扫描次数多、挖掘过程中频繁项集丢失以及生成效率低等缺陷。

针对以上问题，国内外学者从改变数据结构和矩阵压缩两方面提出解决方案。Han J等参考Huffman树结构，利用与根节点距离的思想，提出一种基于模式增长的FP-Growth算法[2]。将各项按项目支持数大小排序，支持度高则距离根节点近，充分利用了已有的频繁项集。该算法虽然在一定程度上提高了频繁项集的生成效率，但随着项集数量的增加，并不能弥补需要多次扫描数据库的缺陷。Park等提出基于Hash方法的DHP算法[3]，该算法利用数据结构哈希树原理提高了运算效率。当某一叶子节点存放的项集超过预设值时，将该节点裂解为新的叶子节点[4]。该算法中生成的候选项集按照哈希函数分配，一次函数遍历就可以完成项集的统计。但面对海量数据时计数工作量大，且依旧需要多次扫描数据库，所以并不适用与海量数据的挖掘。基于压缩矩阵的Apriori算法利用矩阵表示数据库信息，解决了多次扫描数据库的问题。通过对事务和项集的压缩，降低了候选项集规模[5]。苏姜妍等[6]提出基于压缩矩阵先找出最大频繁k项集，再逐步找出其余频繁项集的算法。付沙等[7]提出基于压缩矩阵的Apriori算法：NCM-Apriori-1。该算法通过聚类技术压缩数据库规模，不需要生成候选项集。但基于压缩矩阵的Apriori算法在矩阵压缩过程中存在数据丢失的问题，进而引起频繁项集遗漏等现象，部分算法在执行过程中会生成大量与频繁项集无关的元素[8]。

本文提出一种基于权值向量矩阵约简的Apriori算法，在数据清洗阶段对项集中各元素赋予权值，有效降低了源数据规模，运算过程中不断约简矩阵，提高了算法的运算效率。

1 关联规则概念和算法原理

1.1 基本概念

关联规则挖掘可表示为：设I={i1,i2,i3…im} 是待挖掘项的集合，T={t1,t2,t3…tn} 是挖掘事务的集合，其中ti(1≤i≤n)[9]。A、B称为T中的关联规则，其中A∈I、B∈I、A∩B=∅，目的是为了找出其中的强关联规则[10]。算法执行初期需要用户定义支持度和置信度，其中支持度指某事务占全部事务的百分比，置信度则表示在包含A事务的同时，包含B事务的百分比。在项的集合中，假设全体事务为T，A⟹B的支持度记作：support(A⟹B)，表示为support(A⟹B)=P(A∪B)，A⟹B的置信度为confidence(A⟹B)，表示为confidence(A⟹B)=P(B/A)[11]。在一次关联规则挖掘中，若T中有关联规则A⟹B满足支持度和置信度均大于等于其对应的最小阈值，则称A⟹B是T中的强关联规则。

本文研究重点在降低源数据规模的同时减少频繁项集的丢失，提高关联规则挖掘效率。

1.2 相关性质和定理

在生成的布尔矩阵中，行代表事务，列代表项目。矩阵中每行“1”的个数，代表该事务的项目数，项目的支持数可用每列中“1”的个数表示。

定理1[12]若矩阵中某项的支持数小于sup，则删除该项对应的列。

定理2[13]若某行项目数为“0”，则删除该项对应的行。

定理3[14]若某频繁k项集集合中项集个数小于k+1，则该频繁项集为最大频繁项集。

2 Apriori算法的改进

2.1 算法改进思想

(1)基于项集重要性和用户感兴趣项集的方法，从数据库所有项集中选取一个子集作为研究对象，将待研究项目集用事务标识号标记，并对各元素赋值。

(2)在频繁k项集生成过程中，首先由事务项目数和项目支持数计算sup，比较各项项目支持数，删除支持数小于sup的项在矩阵中对应的列。此时矩阵为频繁k项集对应的矩阵，由定理3判断该频繁项集是否为最大频繁项集，若不是则重新整理矩阵，统计新矩阵事务项目数，若存在某事务项目数为“0”，则从矩阵中删除该事务行，按照上述方法继续寻找频繁k+1项集。否则终止查找过程。

2.2 算法流程

输入：事务数据库D，最小支持度min-support

输出：关联规则S

算法流程如下：

(1)选择挖掘对象。从事务数据库D中选取待研究项集，对项集中各元素赋予权值。得到挖掘对象D1。

(2)生成与数据库D1对应的布尔矩阵。在矩阵后方添加一列，用于记录事务项目数，在矩阵下方添加一行，记录项目支持数。计算各项支持数sup。若某项支持数小于sup，根据定理1删除该矩阵列。调整矩阵格式，重新计算事务项目数，根据定理2删除统计值为“0”的事务在矩阵中对应的行。此时即为频繁1项集对应的矩阵。

(3)将矩阵中各项将上述矩阵按各项支持数降序排列，得到矩阵D2。将D2中任意两列组合，通过向量间“与”运算，求得各组合的支持数。按照(2)中方法约简矩阵，生成频繁2项集对应的矩阵。调整后记为矩阵D3。

(4)频繁k项集的确定(k>2)，参照上述步骤(1)、(2)的矩阵简化方法。若某频繁项集满足定理3，此即为最大频繁项集，与之对应的矩阵记为Dk+1。

(5)频繁k项集的集合用L表示。由L生成的所有非空集S中，若S中某个项集的最小支持度大于用户定义的最小置信度，则存在强关联规则“S→L-S”。

3 算法分析和实验对比

3.1 算法分析

与基于压缩矩阵的Apriori算法相比，本案优点如下：

(1)基于权值向量矩阵约简的Apriori算法可以基于项集重要性和用户兴趣度从事务数据库D中选择待挖掘子集，并对项集中各元素赋予权值，可针对性的选取与所研究课题关系密切的子集，从数据源降低数据规模。

(2)算法的时间复杂度描述了一个算法的运行时间。基于权值向量矩阵约简的Apriori算法中，频繁项集的生成过程只与矩阵运算有关，将数据库D1生成的布尔矩阵记为Rm×n，该算法的时间复杂度为O(mkn)。基于压缩矩阵的Apriori算法平均时间复杂度为O(wk+1)，w代表项集个数，其值远大于m，且随着运算的进行，项集m呈指数级增长。所以本案时间复杂度远小于基于压缩矩阵的Apriori算法。

(3)基于权值向量矩阵约简的Apriori算法在频繁项集生成过程中，不断删除不符合条件的矩阵行与列。随着k值的增长，频繁k项集对应的矩阵Dk+1结构变的愈简单。

3.2 实例分析

本案选取UCI数据集中的Thyroid+Disease集作为研究对象。首先对数据集做预处理，对项集中元素赋予权值，获得符合数据挖掘要求的目标数据：DS={{ABDE},{ADE},{BDEF},{ABDE},{ACE},{BDE},{BCDE}}设最小支持度为0.3。

(1)将数据按照各项支持数降序排列，添加事务项目数和项目支持数后得到矩阵R

矩阵项集的最小支持数根据定义：sup=ceiling(min sup_count)=ceiling(min-support×n)=3。

(2)根据R求得频繁1项集，按照步骤(1)处理后，重新整理得矩阵R1。

比较矩阵中各列支持数与sup大小，删除支持数小于sup的矩阵列，得到矩阵R1。此即为频繁1项集对应的矩阵

由此可求得频繁1项集L1={{A}，{B}，{D}，{E}}。

(3)根据矩阵R1，求频繁2项集。

按照步骤(3)，选取A和D进行“与”运算

sup_count(A∧D)=min sup-count=3， 所以{A,D}为频繁2项集。重复上述步骤可得频繁2项集为：L2={{AD},{AE},{BD},{BE},{DE}}。

(4)按照步骤(4)的流程，求频繁3项集。

由定理1得矩阵R2如下所示

频繁3项集的候选项集为：C3={{ABD},{ABE},{ADE},{BDE}} 求得各组合支持数分别为：count(ABE)=2，count(ACE)=3,count(ADE)=2，count(BDE)=5， 对比sup，可得频繁3项集为：L3={{ABE},{BDE}}。

该频繁项集中，项集个数小于4，符合定理3要求，所以此频繁3项集为最大频繁集。又存在L=L1∪L2∪L3， 由此证明该算法可行。

3.3 挖掘结果分析

利用3.2中数据集，设计如下对比实验，在不同支持度下统计两种算法生成的频繁项集数量。

算法执行过程中一个重要因素是产生候选项集的数量，因为数据预处理可能会造成边缘数据或重要数据的丢失，若两算法产生的候选项集接近，则证明该算法可行。实验结果如图1所示，由图可知，在相同支持度下基于权值向量矩阵约简的Apriori算法产生的频繁项集数量比基于压缩矩阵的Apriori算法多，随着用户预设最小支持度的提高，两种算法生成的频繁项集数量趋于相等。

图1 改进后的Apriori算法与基于压缩矩阵的Apriori算法产生候选项集数量对比

3.4 算法执行效率分析

为比较基于压缩矩阵的Apriori算法与基于权值向量矩阵约简的Apriori算法的执行效率，从IBM Quest Market-Basket Synthetic Data Generator生成3组项数为50，平均事务长度为0.6，事务数为2000，支持度为45%的数据。设计4组实验，分别控制实验中项数、密集度、事务数和支持度，记录并对比两种算法的运行时间。对比结果如图2～图5所示。

由实验结果可知，改进后的Apriori算法在各支持度下均无频繁项集丢失的问题，且算法运行时间减少提高了运算效率。

图2 项数不同时运行时间对比

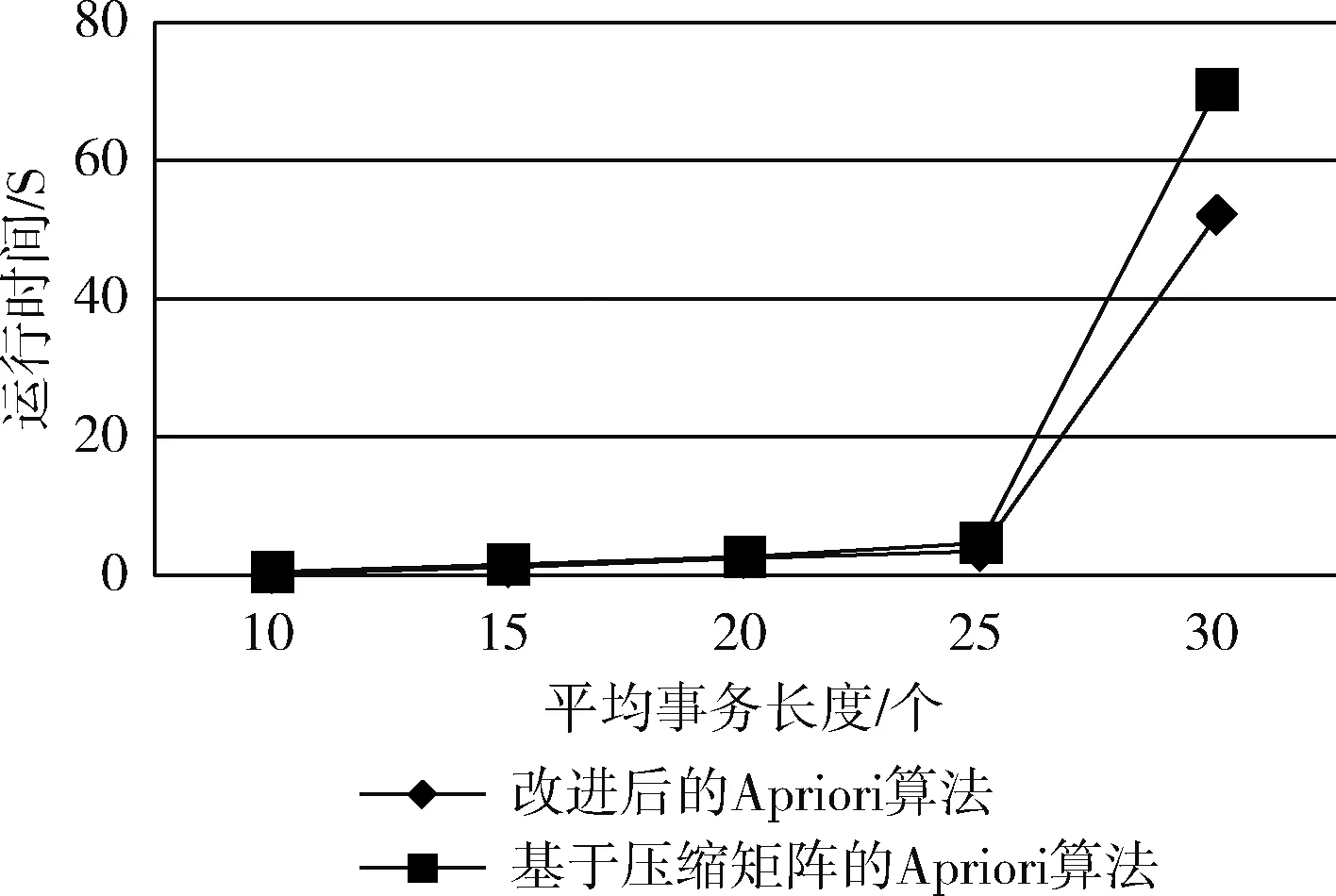
图3 密集度不同时运行时间对比

图4 事务数不同时运行时间对比

图5 支持度不同时运行时间对比

4 结束语

基于权值向量矩阵约简的Apriori算法，通过项集重要性和用户感兴趣度选取挖掘对象，从数据源处降低了数据规模。矩阵约简的思想简化了矩阵结构，避免了候选项集重复生成。与基于压缩矩阵的Apriori算法相比，没有与频繁项集无关元素的生成，提高运算效率的同时不会造成频繁项集的丢失。但该算法在执行前期需要对源数据做筛选等工作，对海量数据可能有一定局限性，所以接下来的工作主要是该算法在海量数据挖掘中的应用研究。

[1]LIU Haiyan,WANG Chao,NIU Junyu.An improved feature selection algorithm based on conditional mutual information[J].Computer Engineering,2012,38(14):36-42(in Chinese).[刘海燕,王超,牛军钰.基于条件互信息的特征选择改进算法[J].计算机工程,2012,38(14):36-42.]

[2]Han J,Pei J,Yin Y.Mining frequent patterns without candidate generations[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data,2012:1-12.

[3]YANG Yanxia,FENG Lin.Parallel DHP data analysis method based on Hadoop platform[J].Computer Application,2016,36(12):3280-3284(in Chinese).[杨燕霞,冯林.基于Hadoop平台的并行DHP数据分析方法[J].计算机应用,2016,36(12):3280-3284.]

[4]Zhang R,Wang H.Research of commonly used association rules mining algorithm in data mining[C]//International Conference on Internet Computer & Information Service.IEEE Computer Society,2015:219-222.

[5]LI Zhiliang.Research and application of Apriori algorithm based on clustering and compression matrix[D].Suzhou:Soochow University,2013(in Chinese).[李志亮.基于聚类和压缩矩阵的Apriori算法的研究与应用[D].苏州:苏州大学,2013.]

[6]Sun jiangyan.An improved K-means clustering algorithm for the community discovery[J].Journal of Software Enginee-ring,2015,9(2):242-253.

[7]FU Sha,LIAO Minghua,SONG Dan.An improved Apriori algorithm based on compressed matrix[J].Microelectronics and Computer,2012,20(4):93-96(in Chinese).[付沙,廖明华,宋丹.基于压缩矩阵方式的Apriori改进算法[J].微电子学与计算机,2012,20(4):93-96.]

[8]SUN Fengxiao,NI Shihong,XIE Chuan.An improved Apriori algorithm based on matrix[J].Computer Simulation,2013,30(8):245-249(in Chinese).[孙逢啸,倪世宏,谢川.一种基于矩阵的Apriori改进算法[J].计算机仿真,2013,30(8):245-249.]

[9]YAN Zhen,PI Dechang,WU Wenhao.Research on frequent itemsets mining algorithm for high-dimensional sparse data[J].Computer Science,2011,38(6):183-186(in Chinese).[闫珍,皮德常,吴文昊.高维稀疏数据频繁项集挖掘算法的研究[J].计算机科学,2011,38(6):183-186.]

[10]Tabakhi S.An unsupervised feature selection algorithm based on ant colony optimization[J].Engineering Applications of Artificial intelligence,2014,32(2):112-123.

[11]LUO Dan,LI Taoshen.An improved Apriori algorithm based on compression matrix[J].Computer Science,2013,40(12):75-80(in Chinese).[罗丹,李陶深.一种基于压缩矩阵的Apriori算法改进研究[J].计算机科学,2013,40(12):75-80.]

[12]REN Weijian,YU Bowen.Improvement of Apriori algorithm based on matrix reduction[J].Computer and Modernization,2015,31(9):5-9(in Chinese).[任伟健,于博文.基于矩阵约简的Apriori算法改进[J].计算机与现代化,2015,31(9):5-9.]

[13]PAN Guo.A classification algorithm based on regularized mutual information to improve input feature[J].Computer Engineering and Applications,2014,50(15):25-29(in Chinese).[潘果.基于正则化互信息改进输入特征的分类算法[J].计算机工程与应用,2014,50(15):25-29.]

[14]LI Rui,KANG Liangyu,GENG Hao.Improvement of data-based association rules algorithm[J].Science & Technology and Engineering,2012,8(2):148-153(in Chinese).[李瑞,康良玉,耿浩.基于数据的关联规则算法的改进[J].科学技术与工程,2012,8(2):148-153.]