基于关联度与引力的复杂网络社区发现方法
2018-03-19龙浩,赵瑛
龙 浩,赵 瑛
(江西师范大学 软件学院,江西 南昌 330029)
0 引 言
现实世界中很多内部单元间存在丰富关联的复杂系统都可表示为网络,如人际关系网、科研合作网等社会系统,电力网、交通网等技术系统,神经网、蛋白质作业网等生物系统,论坛、博客、社交网络等互联网应用系统。研究结果表明[1],复杂网络除了普遍具有小世界、无尺度等统计特征,还有极为重要的社区结构特征[2]。同一社区中的节点,有着较高的连边密度,而社区之间的节点,只有少量节点存在连边。社区结构是复杂网络的中观结构,把微观个体和宏观整体衔接起来,对于揭示复杂网络中的社区构成和社区彼此间关联有着重要意义,有利于加深人们理解复杂系统内部的层次结构和功能特征。近年来社区发现已成为系统科学、社会分析、信息搜索等领域的研究热点。
目前的复杂网络社区发现方法大致可分为3大类:
(1)优化方法。通过定义社区划分的全局目标函数,以达到或接近目标函数最大值作为社区划分结果。淦文燕等[3]引入拓扑势场来描述网络节点之间的联系,联系密切的节点处于势场高处,可以通过查找势值较高的节点可以找出社区;Rodrigo等[4]将社区划分结果与社区内部期望进行比较,提出用Surprise函数来评价社区划分结果;冷作福[5]基于局部贪婪优化技术,提出了求解这类函数定义的社区划分问题的算法。模块度Q函数[6]是目前使用最广泛的社区划分评价,以社区内部连接与随机连接的差异最大化来评价社区,文献[7-9]探讨了用群体智能算法来求解模块度Q函数,实现网络的社区划分。优化方法的难点在于定义合适的目标函数,且容易陷入局部极值,多数情况下最优社区划分方案未必取得最优的目标函数值。
(2)人工智能方法,主要包括和聚类方法模型匹配方法。聚类方法通过定义网络节点间、连边间的相似函数,采用聚类算法对节点或连边归类,将相似程度比较大的节点划分到同一社区[10]。边图划分[11]将社区视为关系密切边的集合,通过定义边的相似度函数来对边集进行聚类,再将边划分结果转化为相应的节点社区;文献[12]通过二阶段聚类实现重叠社区的发现。模型匹配算法使用混合模型[13]、随机块模型[14]来拟合真实网络,并用最大期望算法、改进的最大期望算法或Gibbs采样算法来求解社区参数。聚类方法的缺陷在于容易出现社区冗余,相似性指标的设计也是困扰研究者的一个问题。模型匹配方法能够适应不同类型的网络,但算法复杂性极大限制了它在大型网络上的应用。
(3)启发式方法,主要包括裂解方法或局部扩充方法类发现社区。裂解方法通过找到并删除社区间的连边来发现社区,GN算法[15]认为边介数大的连边往往是社区之间的连边,通过逐步找出并删除最大边介数的连边来分割网络;文献[16]用连边相似度来衡量连边隶属社区的程度,通过迭代删除社区之间的连边来获得网络社区划分结果;局部扩展方法从网络特点节点或结构出发,不断向外扩充形成社区;LFM算法[17]随机选择一个节点开始扩张,直至局部适应度函数最优为止,迭代这一过程直到没有剩余节点;文献[18]从子结构出发来扩充社区,并用局部适应度函数对扩充过程进行调整;Raghavan等[19]提出标签传播思想来识别社区;文献[20]通过发现网络环路并计算紧密值,以此作为网络社区的依据;文献[21]根据力导向模型的原理,通过计算社区与节点之间的作用力来决定节点的社区归属;其它的方法包括矩阵分解方法、特征向量分析的谱方法等等。
复杂网络的社区发现本质上是一个NP-hard问题。对于这类大规模复杂问题,启发式方法能够获得较好的性能,因此目前大部分关于复杂网络社区挖掘的成果和论文都基于这类方法。本文提出了一种网络社区发现算法,通过分析连边特征,定义关联度作为评价连边两端节点关联程度和连边在网络中重要程度的度量,将互连的高关联度节点构成社区骨架;对边缘节点,将它与社区骨架的关联度体现为引力,将它们逐步分级并归入引力最大的社区。并通过实验验证了算法对网络社区挖掘问题的有效性和高效性。
1 基于关联度和引力社区挖掘算法
1.1 基本思想
复杂网络中的节点在社区中所起的作用是不同的,既有边缘节点,也有核心节点。核心节点与同一社区的其它核心节点联系密切,这是社区得以形成和维持的基础,也是网络中多个社区呈现的原因。边缘节点对核心节点有较高的依赖性,通过社区中的核心节点参与到社区中。
1.2 基本概念
复杂网络可以抽象为图模型,并用二元组G=
定义1 链接关联度是连边两端互联节点关系程度及连边在网络中重要程度的一种度量。是两个节点之间直接和间接连接数与两节点中较小度的比值
(1)
关联度反映了连边两端网络节点通过第三方加强彼此关联的程度。aij是它们之间的邻接项,ki,kj是它们的度;显然0≤βij≤1。当βij=0时,两节点之间的最短路径≥3。
定义2 核心节点。对于给定的节点vi,如果满足条件
(2)
其中,threshhold是一个给定的常数,则vi为社区核心节点。同一社区内的核心节点通过较高关联度的连接互连起来,构成社区骨架;不同的社区骨架或者没有直接的连接、或者连边的关联度很低。
定义3 定级系数。节点vi的定级系数定义为它与社区骨架节点和已定级节点的连边占自身度的比例
(3)
{centero,center1,center2,…,centerq} 是已定级节点集合,其中center0表示节点vi的邻居节点中设置为社区骨架节点的节点集合。如果δvi≥δ0(δ0是定级系数阀值),则称vi是q+1级社区节点,即vi∈centerq+1。
定义4 引力。反映未归类节点对社区的依赖程度
(4)

对于q级的未归类节点vi∈V,g1(vi)=maxjγ(vi,uj)→vi∈ul。 即vi被归入对其引力最大的社区中。
1.3 社区发现算法
基于关联度和引力的社区发现算法分两个阶段:首先通过计算连边关联度找出所有核心节点,把互联的核心节点组合在一起构成社区骨架;根据定级阀值δ0对未归类的边缘节点进行定级,并根据给定的距离系数dvi,ujw和引力参数t1,t2,…,tQ,计算不同社区uj对q级的边缘节点vi的引力γ(vi,uj),将节点归入对其引力最大的社区。继续定级q+1级边缘节点并进行引力计算,直到所有边缘节点全部归类。
算法1:社区骨架的生成
输入:图G连边数组L,社区数K,关联度阈值t;
输出:社区骨架S,关联度数组RL;
(1)根据连边数组L构建网络的节点邻居数组链表LL;
(2)计算网络中各个节点的度;
(3)计算每条连边的关联度,与L一起构成关联度数组RL;
(4)筛选所有大于关联度阈值t的连边;
(5)对于筛选的每条连边,如果两节点均不属于任何社区, |S|=|S|+1, 建立一个新社区并将两个节点归入该社区;如果一个节点已归属某一已有社区,将另一节点也归入该社区;如果两节点分属不同社区,合并这两个社区, |S|=|S|-1;
算法2:边缘节点的社区归属
输入:社区骨架S,关联度数组RL,定级系数阀值δ0,引力参数t1,…,tm;
输出:社区划分结果S;
(1)i=1,根据社区骨架找出边缘节点集V1;
(2)计算各边缘节点的定级系数,如果定级系数超过阀值,将节点保留在Vi中,否则将其放入Vi+1;
(3)任取Vi中的节点vi,计算各个社区对其引力γ(vi,uj);将节点vi归入引力最大的社区;
(4)如果Vi不为空,转步骤(3);
(5)i=i+1,如果Vi不为空,转步骤(2),否则结束。
1.4 算法复杂性分析
在算法1中,以数组存储各个节点的度、连接和关联度。步骤(1)、步骤(2)、步骤(4)、步骤(5)的时间复杂度为O(m),步骤(3)的时间复杂度为O(d2m)(d是节点平均度),所以算法1的时间复杂度为O(d2m)。在算法2中,步骤(1)的时间复杂度为O(m),步骤(2)~步骤(5)的时间复杂度为O(n)。所以社区划分算法的总时间复杂度是O(d2m+n)。
2 实验与结果分析
本文算法在win7平台上采用MATLAB R2012a进行开发。运行环境为Intel 2.1 GHz Processor,4 GB RAM。为简化起见,本文规定在所有网络上,引力参数t1=t2=,…=tQ=1。对于真实网络社区划分,用划分精确度(Precision=nright/n, 其中nright是正确分类的节点数目)进行结果评价;对于人工网络,采用NMI(normalized mutual information)进行结果评价,NMI定义参照文献[22]。
2.1 真实基准网络
为验证基于关联度与引力的复杂网络社区发现方法的有效性,采用两个社区成员明确的真实复杂网络数据集Zachary、Dolphins[23]进行检验。
2.1.1 Zachary网络
Zachary是一个描述空手道俱乐部成员的网络数据集,广泛用于复杂网络社区划分结果的验证。网络节点表示俱乐部成员,连边表示他们之间的朋友关系,网络共有34个成员。
图1是Zachary网络在参数P=2,threshhold=0.7,δ0=0.5下的最终社区划分结果。加粗连线是社区核心节点的连接,小圆和方框分别表示两个不同社区的节点,实心表示社区核心节点,空心表示社区边缘节点。从图中可以看到,左边社区中除节点{20}是边缘节点外,其它节点均为核心节点;右边社区中节点{10,25,26,28,29,32}是边缘节点,且{10,26,28,29,32}是一级边缘节点,{25}是二级边缘节点,其余节点是核心节点。从图中可以看到,节点{32}虽然具有较高的度(度为6),但由于它所有连边的关联度值均低于阈值,因此并不是社区核心节点。实验结果表明,本算法的社区划分结果够很好地符合实际情况,社区划分正确率为100%。
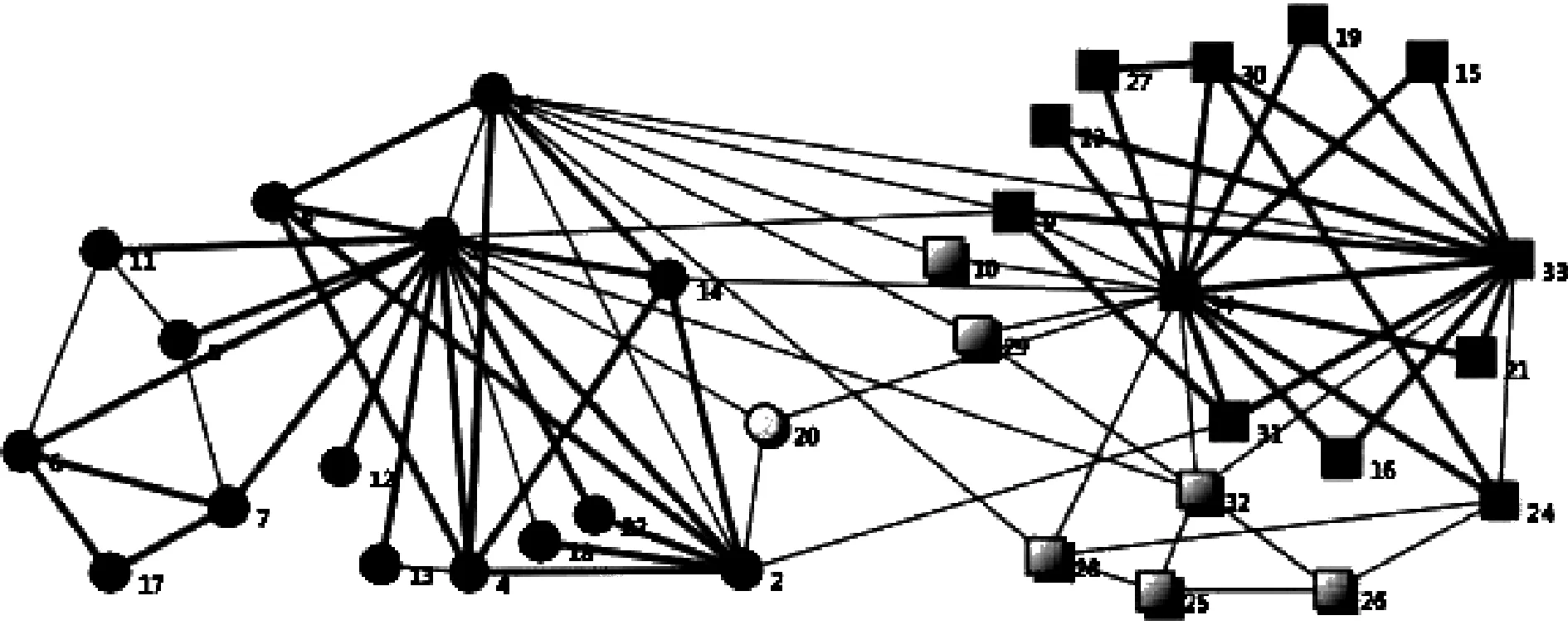
图1 Zachary的社区划分(P=2,threshhold=0.7,δ0=0.5)
2.1.2 Dolphins网络
Dolphins网络也是研究复杂网络社区发现问题的常用真实网络。该网络包含两个海豚家族共62个成员,两个家族分别包括42、20个成员。
图2是Dolphins网络在参数P=2,threshhold=0.5,δ0=0.5的本文算法社区划分结果。加粗连线是社区核心节点的连接,小圆和方框分别表示两个不同社区的节点,实心表示社区核心节点,空心表示社区边缘节点。从图中可以看到,左边社区有{3,37,40,45,47,50,54,56,62}是边缘节点,且它们均为一级边缘节点;右边社区仅有节点{57}是一级边缘节点。边缘节点{37}虽然有较高的度(度为7),但由于它所有连边的关联度值均低于阈值,因此并不是社区核心节点。实验结果表明,算法划分结果很好地符合实际情况,社区划分的正确率为100%。
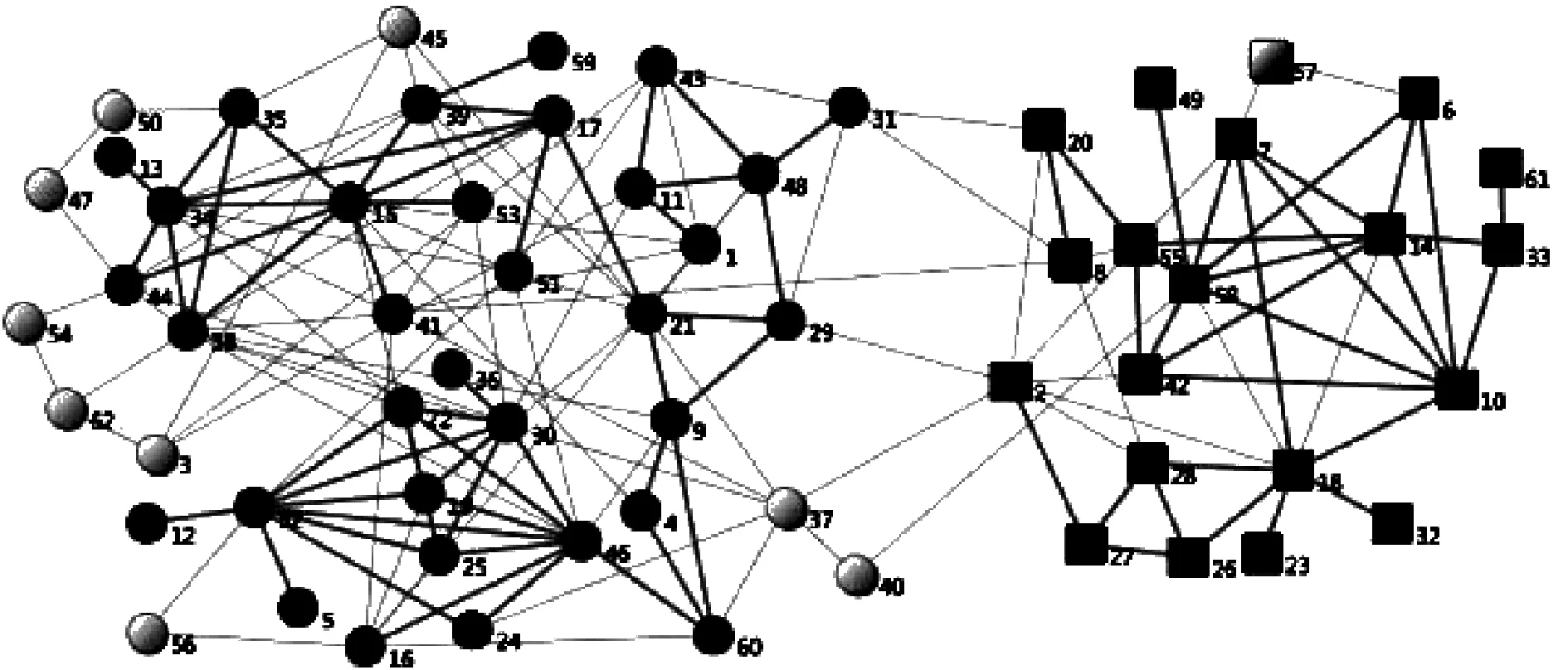
图2 Dolphins的社区划分结果(P=2,threshhold=0.5,δ0=0.5)
两个真实网络的实验结果表明了算法的有效性,且划分结果能够清晰辨识出核心节点、不同分级的边缘节点,能够方便地明确节点在社区中的作用和地位。
2.2 人工合成网络
为评估算法的有效性,本文利用基准网络模型[24]作为数据生成器,并用NMI对算法挖掘社区的精度进行评估。实验生成3组无权无向图数据。第1组数据主要用于测试不同的边缘节点定级系数阈值(分别为0.2,0.3,0.4,0.5,0.6)对最终社区划分精度的影响;第2组数据用于比较本文算法(δ=0.4)(与LTA算法[20](a=3)、FDCD算法[21]的社区划分精度;第3组数据用于比较本文算法(δ=0.4)与LTA算法(a=3)、FDCD算法的运算效率。
(1)第1组数据设置结点个数为128,网络结点最大度为30,社区最小最大规模分别为20,50,社区间重叠结点比例为0.05,网络结点度分布指数为2,网络社区规模分布指数为1。网络结点平均度分别为5,10,15,重复生成10个网络,最终社区划分精度是是10个网络上的平均值。
(2)第2组数据网络结点平均度分别为{5,7,9,11,13,15},其它参数与第1组数据的设置完全相同。每种配置生成10个网络,最终几种算法的社区划分精度是10个网络上的平均值。
(3)第3组数据节点为{500,1000,2000,3000,4000,5000},节点平均度为10,其它参数与第1组相同。每种配置运行10次,得到10个网络,最终几种不同算法的运算时间是10个网络上的平均值。
从图3可以看到,定级系数阈值对网络的社区划分精度有很大影响。总体而言,在不同节点平均度的网络中,都是随着定级系数的阈值增大而降低。这是因为定级系数阀值越高,更多的边缘节点可能因为与骨架节点和已定级边缘节点的连接的比例过低,导致无法定级并归类。
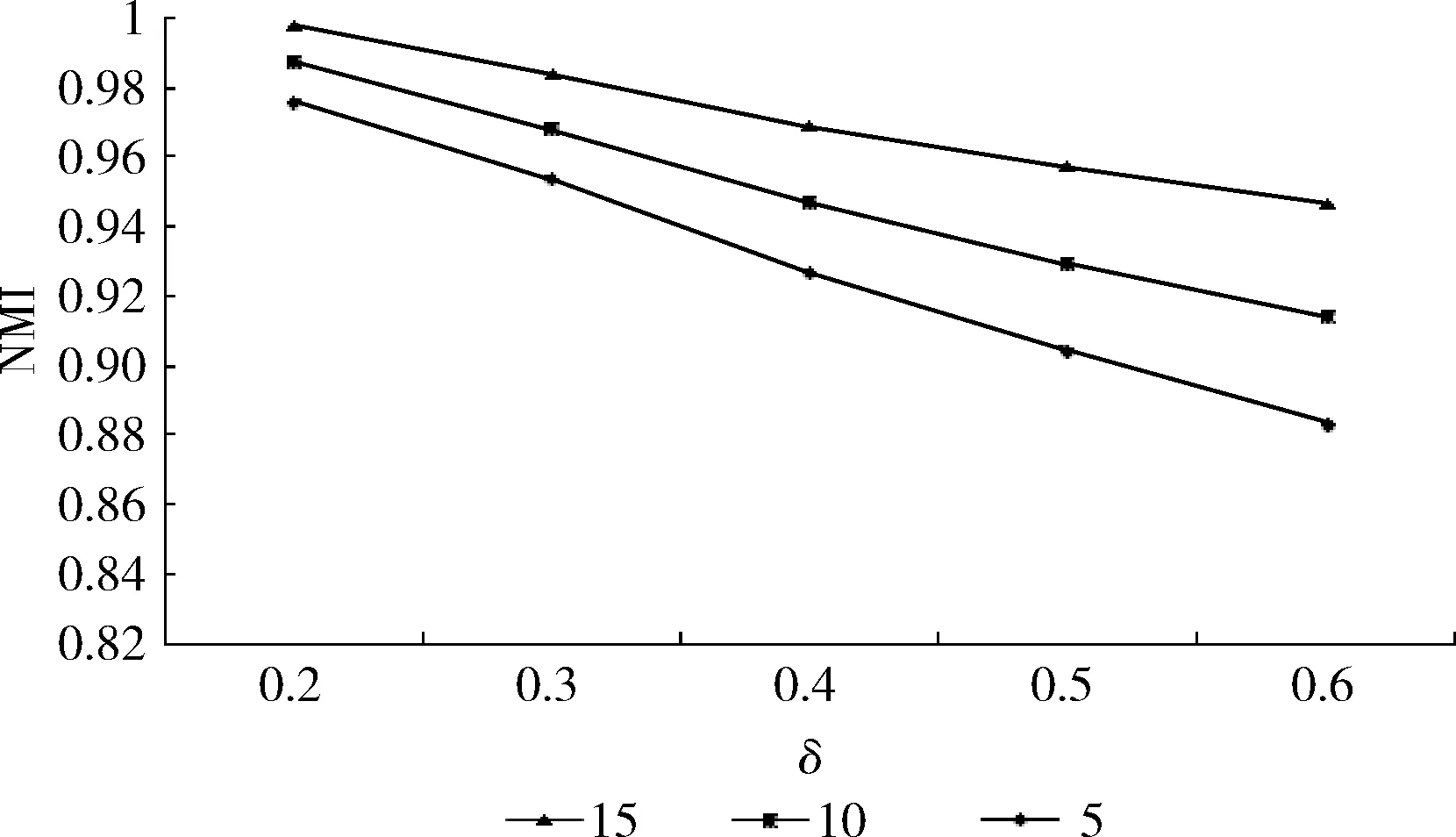
图3 不同定级系数下网络的社区划分精度
图4是第2组数据下,本文算法与LTA算法、FDCD算法的社区划分精度比较。从图中可以看到:①本文算法受人工网络的节点平均度的影响很小,始终保持在较高的划分精度水平。LTA算法和FDCD算法的精度都随网络结点平均度的增大而快速降低;②在不同结点平均度情况下,本文算法划分精度最高,LTA算法次之,FDCD算法最低。这是因为本文算法以连接的关联度来评价节点是否是核心节点,LTA算法以环路个数评价节点是否核心,FDCD算法以节点的邻居数为引力计算的基础,网络结点平均度越大,社区之间出现大度节点的可能性越大,LTA算法和FDCD算法都很可能将这种节点视为社区核心节点,因此对精度有很大影响。
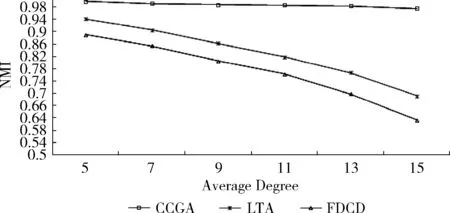
图4 3种算法最终社区划分精度比较
图5是第3组数据下,3种算法的运算效率比较。从结果可以看到,本文算法与LTA算法效率相近,远高于FDCD算法。LTA算法和本文算法的运算时间都随网络节点数近似线性增长;而FDCD算法的运行时间随节点数快速增长。
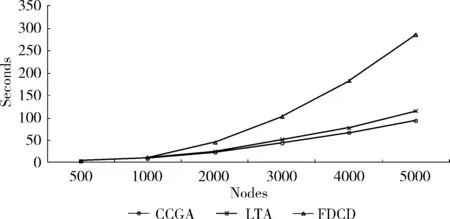
图5 3种算法效率比较
3 结束语
针对复杂网络的社区挖掘问题,根据连边的局部网络信息,研究了网络中互连节点之间的关系,并用关联度进行衡量;关联度同时能够用于度量连边在网络中的重要程度。提出一种复杂网络社区发现算法:算法选择具有高关联度的连边两端节点作为核心节点,互连的核心节点构成社区骨架,再根据引力确定边缘节点的分类。由于社区骨架稳定,保证最终社区划分结果稳定。实验结果表明,算法具有很高的划分精度和近似线性的计算复杂度。实际网络的社区划分结果也显示本文算法避免了其它局部扩展方法可能将大度的边缘节点视为社区核心节点的问题。今后工作将围绕两方面展开,一是定义基于关联度的社区划分评价标准,二是将关联度用于复杂网络重叠社区挖掘。
[1]Newman MEJ.Communities,modules and large-scale structure in networks[J].Nature Physics,2012,8(1):25-31.
[2]LIU Dayou,JIN Di,HE Dongxiao,et al.Community mining in complex network[J].Journal of Computer Research and Development,2013,50(10):2140-2154(in Chinese).[刘大有,金弟,何东晓,等.复杂网络社区挖掘综述[J].计算机研究与发展,2013,50(10):2140-2154.]
[3]GAN Wenyan,HE Nan,LI Deyi,et al.Community disco-very method in networks based on topological potential[J].Journal of Software,2009,20(8):2241-2254(in Chinese).[淦文燕,赫南,李德毅,等.一种基于拓扑势的网络社区发现方法[J].软件学报,2009,20(8):2241-2254.]
[4]Rodrigo A,Ignacio M.Surprise maximization reveals the community structure of complex networks[J].Scientific Reports,2013,3(1):1060.
[5]LENG Zuofu.Community detection in complex networks based on greedy optimization[J].Acta Electronica Sinica,2014,42(4):723-728(in Chinese).[冷作福.基于贪婪优化技术的网络社区发现算法研究[J].电子学报,2014,42(4):723-728.]
[6]Newman MEJ.Fast algorithm for detecting community structure in networks[J].Physical Review E,2004,69(6):066133.
[7]Shang R,Bai J,Jiao L,et al.Community detection based on modularity and an improved genetic algorithm[J].Physica A,2013,392(5):1215-1231.
[8]Parsa MG,Mozayani N,Esmaeili A.An EDA-based community detection in complex networks[C]//7th International Symposium on Telecommunications,2014:476-480.
[9]Ma L,Gong M,Liu J,et al.Multi-level learning based memetic algorithm for community detection[J].Applied Soft Computing,2014,19(2):121-133.
[10]YANG Bo,LIU Dayou,LIU Jiming,et al.Complex network clustering algorithms[J].Journal of Software,2009,20(1):54-66(in Chinese).[杨博,刘大有,LIU Jiming,等.复杂网络聚类方法[J].软件学报,2009,20(1):54-66.]
[11]ZHU Mu,MENG Fanrong,ZHOU Yong.Density-based link clustering algorithm for overlapping community detection[J].Journal of Computer Research and Development,2013,50(12):2520-2530(in Chinese).[朱牧,孟凡荣,周勇.基于链接密度聚类的重叠社区发现[J].计算机研究与发展,2013,50(12):2520-2530.]
[12]JIANG Shengyi,YANG Bohong,LI Minmin,et al.Overlapping community detection algorithm based on two-stage clustering[J].Pattern Recognition and Artificial Intelligence,2015,28(11):983-991(in Chinese).[蒋盛益,杨博泓,李敏敏,等.基于二阶段聚类的重叠社区发现算法[J].模式识别与人工智能,2015,28(11):983-991.]
[13]Ren W,Yan G,Liao X,et al.Simple probabilistic algorithm for detecting community structure[J].Physical Review E,2009,79(2):036111.
[14]Abbe E,Bandeira AS,Hall G.Exact recovery in the stoc-hastic block model[J].IEEE Transactions on Information Theory,2016,62(1):471-487.
[15]Girvan M,Newman MEJ.Community structure in social and biological networks[J].Proc of National Academy of Science,2002,9(12):7821-7826.
[16]JIN Di,LIU Jie,JIA Zhengxue,et al.K-Nearest-neighbor network based data clustering algorithm[J].Pattern Recognition and Artificial Intelligence,2010,23(4):546-551(in Chinese).[金弟,刘杰,贾正雪,等.基于K最近邻网络的数据聚类算法[J].模式识别与人工智能,2010,23(4):546-551.]
[17]Chen D,Shang M,Lv Z,et al.Detecting overlapping communities of weighted networks via a local algorithm[J].Physica A:Statistical Mechanics and its Applications,2010,389(19):4177-4187.
[18]Lee C,Reid F,McDaid A,et al.Detecting highly overlapping community structure by greedy clique expansion[C]//Proc of the 4th Int Workshop on Social Network Mining and Analysis.New York:ACM,2010:33-42.
[19]Raghavan UN,Albert R,Kumara S.Near linear-time algorithm to detect community structures in large-scale networks[J].Physical Review E,2007,76(3):036106.
[20]LIU Dayou,YANG Jianning,YANG Bo,et al.Community mining from complex networks based on loop tightness[J].Journal of Jilin University:Eng and Technol Ed,2013,43(1):98-105(in Chinese).[刘大有,杨建宁,杨博,等.基于环路紧密度的复杂网络社区挖掘方法[J].吉林大学学报(工学版),2013,43(1):98-105.]
[21]SHUI Chao,CHEN Honghui,CHEN Tao,et al.A community detect algorithm on force-directed model[J].Journal of National University of Defense Technology,2014,36(4):163-168(in Chinese).[水超,陈洪辉,陈涛,等.力导向模型的复杂网络社区挖掘算法[J].国防科技大学学报,2014,36(4):163-168.]
[22]Danon L,Diaz-Guilera A,Duch J,et al.Comparing community structure identification[J].Journal of Statistical Mecha-nics:Theory and Experiment,2005(9):P09008.
[23]Newman MEJ.Network data[EB/OL].[2013-04-19].http://www-personal.umich.edu/~mejn/netdata/.
[24]Lancichinetti A,Fortunato S.Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities[J].Physical Review E,2009,80(1):016118.
