复杂预应力对立管参激振动特性的影响分析

王 威，陈炉云

（1.中国舰船研究设计中心，武汉 430064；2.上海交通大学 海洋工程国家重点实验室，上海 200240）

0 引 言

立管结构是海洋平台系统连接海面与海底的通道，承担着油气输送的功能，是海洋油气开发的关键部件。海洋平台随着海洋波浪的作用而发生升沉运动，给立管顶端一个位移时程响应，引起立管轴向力随浮体运动而发生变化，并导致立管在水平方向振动，这种现象称为参激振动。参激振动可引发立管的参数共振并导致结构破坏。Hsu[1]最早关注海洋细长结构物的参激共振问题，对限制海域的缆索的振动不稳定性问题进行了研究。张杰等[2-3]分析了立管固有振动特性的变化规律，对比了设计参数对固有振动特性的影响。唐友刚等[4]研究了立管在剪切流中的参激-涡激耦合振动问题，分析了参数激励对横向涡激振动的影响。邵卫东等[5]对变张力作用下的立管结构振型进行了对比，分析考虑重力因素后的结构特性的变化。Kuiper[6]分析了立管内外流体压力差、结构阻尼、截面扭转和剪切变形等因素对立管参激振动的影响。Chen等[7]以8种常见边界约束为例，探讨了边界条件对立管固有振动特性的影响。Chatjigeorgiou[8-9]分析了结构阻尼对立管参数激励振动稳定性的影响，研究参数激励频率为立管一阶固有频率2倍时的结构响应。Park等[10]对立管的参激-涡激耦合振动问题进行了时域分析，对比了水深、环境条件和立管模态对振动幅值的影响。杨和振等[11]对参数激励下深海立管的参量不稳定性进行探讨，分析阻尼参数对参激振动稳定区域的影响。Fujiwara等[12]采用大比尺模型试验，验证了参激参数对涡激振动的影响，并进一步给出了数值计算的结果。

立管结构是一个复杂的焊接壳体结构，结构中通常都存在一定的预应力。预应力产生的原因有：焊接残余应力、静水压力、油气压力和其他静载荷等，预应力大小及方向随位置而变化，将其定义为复杂预应力。预应力对结构性能有巨大的影响，研究含预应力的结构动力学特性具有重要的理论意义。Chen等[13]通过对非线性方程组的求解，分析了含初应力的结构动力响应问题。Matsunaga[14]基于二维高阶剪切理论，分析了含轴向预应力的简支圆柱壳自由振动问题，对比了剪切效应和转动效应对振动频率的影响。Zeinoddini等[15]将管道内流动水压力定义为均匀静载荷，对比了管内流速对结构响应的影响。Zhang等[16]以圆柱薄壳结构为例，分析了初始预应力、表面压力和结构形状等因素对结构振动的影响。陈炉云等[17]基于应用变分原理分析了含局部预应力的圆柱壳结构动力响应方程和预应力对声辐射功率和声指向性的影响。刘勇[18]建立了含复杂预应力的平板结构和圆柱壳结构的振动微分方程，提出了自由振动和强迫振动的解析方法。

本文基于预应力基本理论，以立管的纯参激振动问题为研究对象，将残余应力、水压静应力及轴向力定义成复杂预应力，分析复杂预应力对立管结构频率、模态等动力特性的影响。

1 立管参激振动基本模型

1.1 顶张力立管概述

对于典型顶张力立管的参激振动分析，首先对立管进行适当假设：立管结构简化为一维梁模型；立管顶部张力是一个与波浪频率相关的函数；立管几何尺寸、材料性质沿长度方向不变；立管的应变很小，应力应变满足线性关系；仅考虑管内流体质量，忽略流速引起的动力效应。

基于上述假设，将立管与海洋平台浮体相连的张紧器简化为一个弹簧机构，该机构将平台对立管的位移激励转化为力激励，定义等效弹簧刚度为K。由于张紧器刚度远小于立管的轴向刚度，立管的两端约束可视为两端铰支边界。以立管顶部为原点建立直角坐标系，定义z方向为立管轴向方向，y方向为立管位移方向，建立立管模型，如图1所示。

1.2 立管参激运动基本方程

根据立管结构基本假设，应用Euler-Bernoulli理论，纯参数激励下的立管运动方程为：

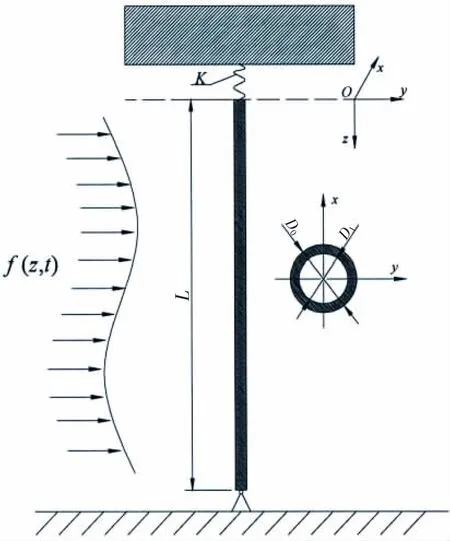
图1 立管模型示意图Fig.1 Simply supported riser

式中：w（ z,t）为立管横向振动位移；T（ z,t）为立管张紧力；cS为立管结构的阻尼系数为立管单位长度上水平外激励力；EI为弯曲刚度，为单位长度的立管结构质量，D0和D1分别为立管的外径和内径，ρs为立管结构材料密度；mf=为单位长度的管内油气质量，ρf为管内油气密度为单位长度的立管附连水质量，ρw为海水密度，Ca为附连水质量系数。

假设立管两端为铰支支撑，则其边界条件满足：

此时，立管张紧力T z,（）t可写成：

2 梁结构预应力模型

立管可简化为Euler-Bernoulli梁结构，并遵循“平断面假定”。下面基于梁结构理论开展含预应力的立管结构应力分析。

2.1 预应力类型

在梁结构动力响应中，结构除受动载荷作用外，还受其它形式的静载荷的作用。可将这些静载荷引起的应力定义成复杂预应力。此外，结构轴向张紧力引起的轴向拉应力也可定义成预应力。此时，结构的预应力包括：梁结构张紧力、静水压力和焊接残余应力，它们满足线性叠加关系：

式中：σT为张紧力引起的应力为结构截面面积，T z,（）t为结构张紧力；σH为静水压力引起的应力，σH=f（）h，h为水深；σR为焊接残余应力，在文中只考虑z方向焊接残余应力，并有σR=σR,z。在文中，只考虑z方向复杂预应力σr=σr,z

2.2 预应力假设

因结构中存在着预应力，其运动方程受预应力与动位移间耦合作用影响。在结构动力响应分析中，设预应力与振动引起的动应力满足线性叠加关系。在预应力作用下，结构静态平衡方程可写成：

式中：σr,z为预应力，P为静外载荷。若预应力为焊接残余应力，则有P=0；若预应力是由静水压力引起，P为静水压力函数，则有为水深；若预应力是由梁结构的张紧力引起，则有P=T（ z,t）。

此时，含预应力的梁结构动力响应运动方程为：

3 基于复杂预应力的梁结构运动微分方程

以梁结构动力响应特性为研究对象，分析预应力与结构振动位移的耦合关系，建立含复杂预应力的梁结构运动控制微分方程，提出梁结构自由振动的求解方法。

3.1 梁结构模型

梁结构的长度为L，其截面面积为S，如图2所示。建立直角坐标系，z轴与梁长度方向重合且位于梁中性层上。定义对称面yOz，梁弯曲发生在yOz平面内。定义垂直z轴的位移w为挠度，其正向与y轴正向相同。

图2 梁结构几何模型Fig.2 Beam geometry model

当梁结构发生振动时，选取梁结构中微元体，其长度为dz。微元体中的力和力矩包括两部分：预应力与位移的耦合力；振动位移引起的力和力矩。对于微单元dz，其轴向截面拉力Nr,z可写成：

根据梁弯曲理论，梁结构任意处应变εz可写成:

式中：w（ z,t）为振动位移。根据虎克定律，正应力σz为

此时，作用在微元体截面上的弯矩可写成:

式中：Mz为σz在梁断面引起的弯矩；I为梁结构惯性矩；E为梁结构材料弹性模量。

3.2 耦合项分析

设结构在z轴方向分布预应力σr,z是变量z的函数。在力平衡条件下，含预应力的结构微元体受力情况如图3所示。

当结构发生振动时，预应力与振动位移相互作用会引起耦合。假设预应力大小和分布在振动过程中保持不变，并引起微元体应变。此时，梁截面单位长度距中性面的变形ly可写成:

根据“平断面假定”，单位长度梁结构体积V可写成：

由（12）式可知，微元体的振动过程中其体积不变，因而截面拉力Nr,z在振动过程中亦不变。当梁结构处于静止状态时，截面拉力Nr,z平行于z轴，且在其他方向上无分量。由于预应力σr,z始终与横截面保持垂直，故预应力不产生新的耦合弯矩和转矩。

受振动位移w的作用，截面拉力Nr,z产生绕y轴的转角，其转角大小为∂w/∂z。此时，截面拉力Nr,z在y方向上的分量ΔNy,z可写成如下形式：

由（13）式可知，分量ΔNy,z是预应力和振动位移的函数，它改变了微元体的力平衡方程，是预应力与振动位移间的耦合力，如图4所示。

图3 预应力引起的截面力Fig.3 Section force caused by pre-stress

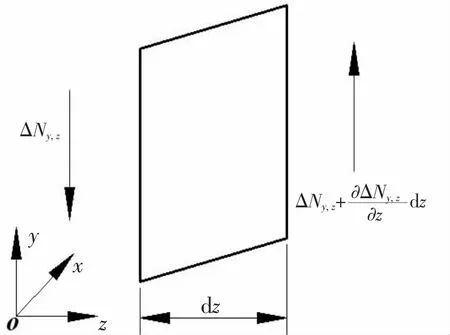
图4 微元体耦合力Fig.4 Element body coupling force

3.3 平衡方程

根据梁结构的小挠度弯曲理论，分析微元体的力和力矩平衡方程。含复杂预应力的弹性梁在z方向的力平衡条件恒满足。在y方向力平衡方程中，有剪力Qz和y方向的耦合力ΔNy,z，其力平衡方程为：

式中：m为微元体结构等效质量。因预应力不产生耦合力矩，即含预应力的弹性梁结构在y方向的力矩平衡条件恒满足。在z方向，力矩平衡方程满足：

将（15）式代入（14）式，可得如下微分形式：

3.4 基于复杂预应力的立管运动微分方程

将（7）、（10）式代入（16）式，则含复杂预应力的梁结构自由振动微分方程可写成：

4 含复杂预应力的梁结构自由振动

下面对梁结构自由振动问题进行分析，开展立管振动特征分析。

4.1 自由振动方程

设梁两端为绞支支撑，满足两端边界条件的位移表达式可写成级数形式：

式中：φ（z）为振形函数；β=π/L，L为梁长度；i为虚数单位；ω为圆频率；Bn为梁结构位移系数；N为级数的项数。

引入正交三角级数 sin（ ξβ z），其中 ξ为正交参数。 将（18）式代入（17）式，利用三角级数的正交性，沿梁从z=0到z=L积分，可得：

4.2 典型梁振动特征

下面以几种典型预应力分布形式为例，分析含复杂预应力的梁结构自由振动特性。

（1）若复杂预应力为σr,z，（19）式可直接简化为简单梁结构的自由振动方程，其特征方程为EI

（2）若复杂预应力为均匀分布，即σr,zS＝T0，则（18）式可简化为复杂梁结构的振动方程，其特征方程为

当σr,z为拉应力时，梁结构的固有频率将升高；当σr,z为压应力时，梁结构的固有频率将降低。

（3）若复杂预应力沿轴向方向变化，它是一维复杂预应力，可用三角函数来拟合：

根据（26）式，其解形式可建立N个方程，将其联立并写成矩阵形式：

（4）设复杂预应力沿轴向方向变化，并用更复杂的三角级数来拟合：

式中：各参数的物理意义与（24）式相同。由于复杂预应力的表达式更为复杂，级数项增多，这导致预应力影响矩阵R发生变化，此时矩阵R不再是稀疏矩阵。由于复杂预应力的级数项是线性相加关系，矩阵R可表示为：

4.3 模态分析

针对典型复杂预应力分布情况，建立两端铰支立管的自由振动特征方程。复杂预应力可用三角级数来拟合，采用（32）式来描述立管结构中复杂预应力具有普适性。含复杂预应力的特征方程为线性方程组，令其特征方程系数的行列式为零，即：

求解（33）式，可获得含复杂预应力的梁结构的固有频率和振型。若结构中不存在预应力，即R=0，（33）式可退化为经典弹性梁自由振动特征方程；若结构中存在着预应力，即不再是对角矩阵。

表1 计算模型参数Tab.1 Parameters of the model system

5 算 例

5.1 立管模型

在开展立管参激振动数值计算中，立管结构基本参数参考文献[2]，如表1所示。

5.2 定轴力下立管振动特性

忽略立管自重影响，立管结构内的轴向拉力为立管顶端静张紧力，即T（ z,t）=T0，复杂预应力为立管结构的振型函数可写成分离变量法计算定轴力下立管振型函数φ（）z。图5所示为立管前三阶振型，振型是标准正弦函数。

图5 立管振型示意图Fig.5 Mode shapes of the riser

5.3 变轴力下立管振动特性

考虑立管自重的影响作用，但忽略平台升沉的影响，内部张紧力沿水深增加而减少，即此时结构内复杂预应力立管结构的振型函数可写成

图6所示为立管前三阶振型，在立管结构应力分布是水深 z的函数时，立管振型有明显变化，它不再是标准正弦函数，振型振幅最大点向海底方向偏移。

图6 立管振型示意图Fig.6 Mode shapes of the riser

5.4 变轴力与残余应力联合作用下立管振动特性

下面分析分布着复杂焊接残余应力且受变轴力作用下的立管结构振动特性。焊接残余应力分布形式如图7所示，其最大值约为149 MPa。应力为正表示为拉应力、应力为负则表示为压应力。

在立管结构中的复杂残余应力的大小可拟合成三角级数。在本研究中，采用20阶级数对焊接残余应力进行拟合，并写成管结构中的复杂预应力可写成将其代入到方程（19）中，可得立管结构的振型函数为

图8所示为含有焊接残余应力的立管结构前三阶振型，此时立管振型不再是标准正弦函数，焊接残余应力使立管的振动振型由光滑的曲线变成带有较多突变的粗糙曲线，靠近海底处更为明显，这表明焊接残余应力影响立管的横向振动。

对比图5、图6和图8可知，在复杂预应力作用下，立管的振型变得更为复杂，复杂预应力对立管横向振动具有重要影响。因此，在立管结构动力响应分析中考虑复杂预应力的影响是十分必要的。

表2所示为三种工况下立管结构前6阶固有频率的对比。

由表2可知，在焊接残余应力作用下，立管固有频率变小。由于存在复杂预应力，立管固有频率值与不考虑预应力的固有频率值相差较大，在前几阶频率影响更为明显。

图7 残余应力分布Fig.7 Distribution of pre-stress

图8 立管振型示意图Fig.8 Mode shapes of the riser

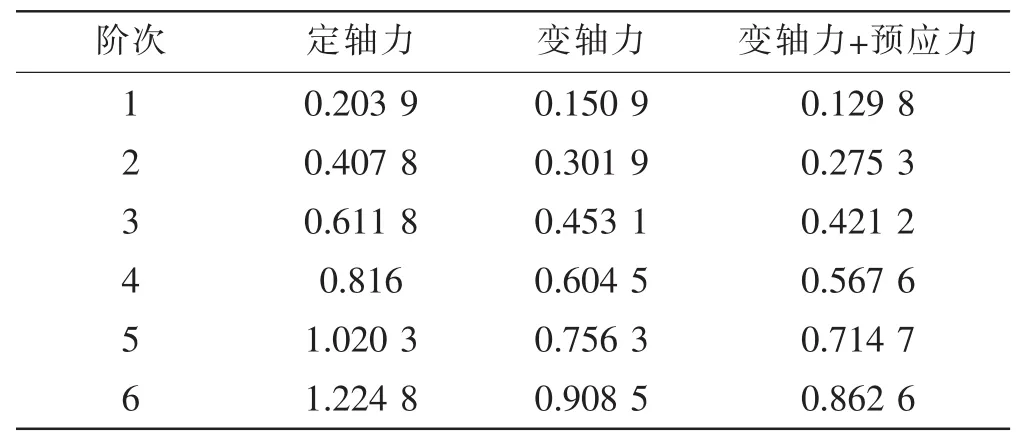
表2 固有频率计算Tab.2 Comparison of natural frequencies of the riser

6 结 论

文章基于预应力理论，开展立管参激振动分析，得出如下结论：在立管振动特性分析中考虑焊接残余应力因素可更为全面地描述结构的力学特性和总体性能；分析复杂预应力对立管振动特性的影响，可为通过控制结构复杂预应力达到实现提高立管结构综合性能的目标提供技术参考。

[1]Hsu C S.The response of a parametrically excited hanging string in fluid[J].Journal of Sound and Vibration,1975,39(3):305-316.

[2]张 杰,唐友刚.深海立管固有振动特性的进一步分析[J].船舶力学,2014,18(1-2):165-171.Zhang Jie,Tang Yougang.Further analysis on natural vibration of deep-water risers[J].Journal of Ship Mechanics,2014,18(1-2):165-171.

[3]Zhang Jie,Tang Yougang.Mathieu instability analysis of deepwater top-tensioned risers[J].Journal of Ship Mechanics,2014,18(9):1142-1150.(English edition)

[4]唐友刚,邵卫东,张 杰,王丽元,桂 龙.深海顶张力立管参激—涡激耦合振动响应分析[J].工程力学,2013,30(5):282-286.Tang Yougang,Shao Weidong,Zhang Jie,Wang Liyuan,Gui Long.Dynamic response analysis for coupled parametric vibration and vortex-induced vibration of top-tensioned riser in deep-sea[J].Engineering Mechanics,2013,30(5):282-286.

[5]邵卫东,唐友刚,樊娟娟,等.考虑浮体升沉及张紧环运动深海立管固有振动特性研究[J].海洋工程,2012,30(2):8-13．Shao Weidong,Tang Yougang,Fan Juanjuan,et al.Study of natural vibration characteristics of deep-water riser considering heave motion of platform and tension-ring’s motion[J].Ocean Engineering,2012,30(2):8-13．

[6]Kuiper G L,Brugmans J,Metrikine A V.Destabilization of deep-water risers by a heaving platform[J].Journal of Sound and Vibration,2008,310(3):541-557.

[7]Chen Y F,Chai Y H,Li X,Zhou J.An extraction of the natural frequencies and mode shapes of marine risers by the method of differential transformation[J].Computers and Structures,2009,87(21-22):1384-1393.

[8]Chatjigeorgiou I K.On the parametric excitation of vertical elastic slender structures and the effect of damping in marine applications[J].Applied Ocean Research,2004,26(1-2):23-33.

[9]Chatjigeorgiou I K,Mavrakos S A.Nonlinear resonances of parametrically excited risers-numerical and analytic investigation for Ω=2ω1[J].Computers and Structures,2005,83(8-9):560-573.

[10]Park H,Jung D H.A finite element method for dynamic analysis of long slender marine structures under combined parametric and forcing excitations[J].Ocean Engineering,2002,29(11):1313-1325.

[11]杨和振,李华军.参数激励下深海立管动力特性研究[J].振动与冲击,2009,28(9):65-78.Yang Hezhen,Li Huajun.Vibration analysis of deep-sea risers under parametric excitations[J].Journal of Vibration and Shock,2009,28(9):65-78.

[12]Fujiwara T,Uto S.Kanada D.An experimental study of the effects that change the vibration mode of riser VIV[C].OMAE 2011-49677.

[13]Chen C S,Cheng W S,Tan A H.Non-linear vibration of initially stressed plates with initial imperfections[J].Thin-Walled Structures,2005,43(1):33-45.

[14]Matsunaga H.Free vibration of thick circular cylindrieal shells subjected to axial stresses[J].Journal of Sound and Vibration,1998,221(l):l-17.

[15]Zeinoddini M,Harding J E,Parke G A R.Dynamic behaviour of axially pre-loaded tubular steel members of offshore structures subjected to impact damage[J].Ocean Engineering,1999,26(10):963-978.

[16]Zhang Y L,Gorman D G,Reese J M.Vibration of prestressed thin cylindrical shells conveying fluid[J].Thin-Walled Structures,2003,41(12):1103-1127.

[17]陈炉云,李磊鑫,张裕芳.含局部预应力的圆柱壳结构声辐射特性分析[J].上海交通大学学报,2014,48(8):772-777.Chen Luyun,Li Leixin,Zhang Yufang.Characteristics analysis of structural-acoustic of cylindrical shell with prestress in local areas[J].Journal of Shanghai Jiaotong University,2014,48(8):772-777.

[18]刘 勇.复杂预应力对圆柱壳结构动力特性影响研究[D].上海:上海交通大学,2014.Liu Yong.A study of the impact on dynamic characteristics of cylindrical shell with complex prestress[D].Shanghai:Shanghai Jiaotong University,2014.