尾后轴承刚度对潜艇结构声辐射特性的影响

刘文玺，周其斗，谭 路，张 恺

（海军工程大学 舰船工程系，武汉 430033）

0 引 言

螺旋桨是潜艇的一个很大的噪声源，它产生噪声的主要方式之一是通过轴系激发艇体结构的振动并由艇体湿表面向水中辐射噪声，螺旋桨激振力通过轴系引起艇体振动和辐射噪声问题是一个螺旋桨、轴系和艇体结构耦合振动的问题，研究难度很大，这方面的研究相对较少，因此，深入开展这方面的研究，对潜艇减振降噪具有重要的意义。

从螺旋桨，经过轴系，到艇体结构，构成了振动传递路径，本文研究在振动传递路径上进行声学设计，控制潜艇辐射噪声。迄今为止，很多学者在这方面的研究取得了一定成果。

控制螺旋桨激振力通过轴系传递到艇体结构最常用的方法是在轴系设置轴向减振器和动力吸振器[1]，Dylejko等[1]、曹贻鹏等[2]和Merz等[3]对轴系—潜艇结构的耦合振动问题开展了研究，在推力轴承位置处使用动力吸振器来降低经由推力轴承传递到潜艇结构的轴系纵向脉动力，分别使用传递矩阵方法、FEM方法和结构有限元耦合流体边界元法建立动力学系统模型，对动力吸振器的结构参数进行优化，达到降低激振力传递的目的。曹贻鹏[5]为了降低螺旋桨轴向激振力引起的潜艇结构辐射噪声，从结构声学设计的角度出发，改变推力轴承基座的结构形式，采用横舱壁作为推力轴承基座，改变了轴向激振力传递路径，最终达到了降低潜艇辐射噪声的目的。李攀硕[6]分析了轴-壳体耦合系统振动固有特性及其随推力轴承刚度的变化规律，并讨论了在轴上实施纵向振动控制的可行性，结果表明，推力轴承刚度改变轴系纵振频率，对纵振能量传递有明显影响，轴系纵向振动不仅会引起壳体纵向共振，还会引起壳体弯曲振动，形成轴—壳纵横耦合模态，轴的纵向振动控制可以减小耦合系统振动。西澳大学的Pan Jie[7]对螺旋桨脉动力沿轴系到简支板的传递特性开展了研究。螺旋桨的激振力是通过试验方法得到的，计及推力轴承的油膜影响，测得了推力轴承刚度与螺旋桨转速的关系，重点研究了伴流场引起的螺旋桨纵向脉动力以及纵向力通过轴系激励弹性板，激起板的振动响应。Cao[8]对轴系—结构的耦合振动系统在螺旋桨脉动力作用下的振动及辐射噪声分布特性开展了研究，并发现不仅螺旋桨纵向脉动力能引起结构的辐射噪声，螺旋桨横向脉动力经过轴系的各个支点轴承也可以将振动能量传递到结构上，引起结构产生较强的辐射噪声，并对其开展研究工作，在此基础上，分析了在螺旋桨激励下结构辐射噪声的消减措施。谢基榕[9]研究了推进器激励的艇体辐射噪声及控制技术。研究结果表明，对于螺旋桨—轴系—艇体这样的耦合振动系统，研究螺旋桨激振力引起的艇体振动和辐射噪声问题，一定要考虑轴系对激振力传递的影响。

上述研究主要集中在：（1）螺旋桨激振力经轴系到艇体的传递规律；（2）在轴系安装动力吸振器以降低螺旋桨轴向激振力向艇体结构的传递；（3）改变推力轴承基座结构形式减弱螺旋桨轴向激振力引起的艇体振动和辐射噪声。

在仔细学习前人研究成果的基础上，本文从以下方面对潜艇结构的振动和声辐射问题做了深入的研究：从结构振动传递路径的声学设计的角度出发，借鉴在机械设备下面安装合适的隔振器以减弱对艇体结构的激振力的设计思想，将轴系上距离螺旋桨最近的尾后轴承看做螺旋桨的弹性支撑，通过改变轴承的刚度，改变潜艇结构振动和辐射噪声的谱峰频率，降低谱峰峰值。通过改变艇体结构的的声学特性，使设备激振力的谱峰频率与结构振动和辐射噪声的谱峰频率错开，从而实现对潜艇辐射噪声的控制。

1 基本方程

1.1 计算模型

以单壳体SUBOFF[11]潜艇模型为研究对象，模型的主要结构参数如表1所示，板厚分布如图1所示，其中耐压壳板厚除舱壁附近是6 mm以外，其余都是4 mm。

采用PATRAN有限元软件对SUBOFF潜艇模型进行有限元建模，其中螺旋桨采用实体单元建模，其他结构主要采用面单元和梁单元进行建模，沿艇体纵向，一个肋骨间距保证至少两排单元。

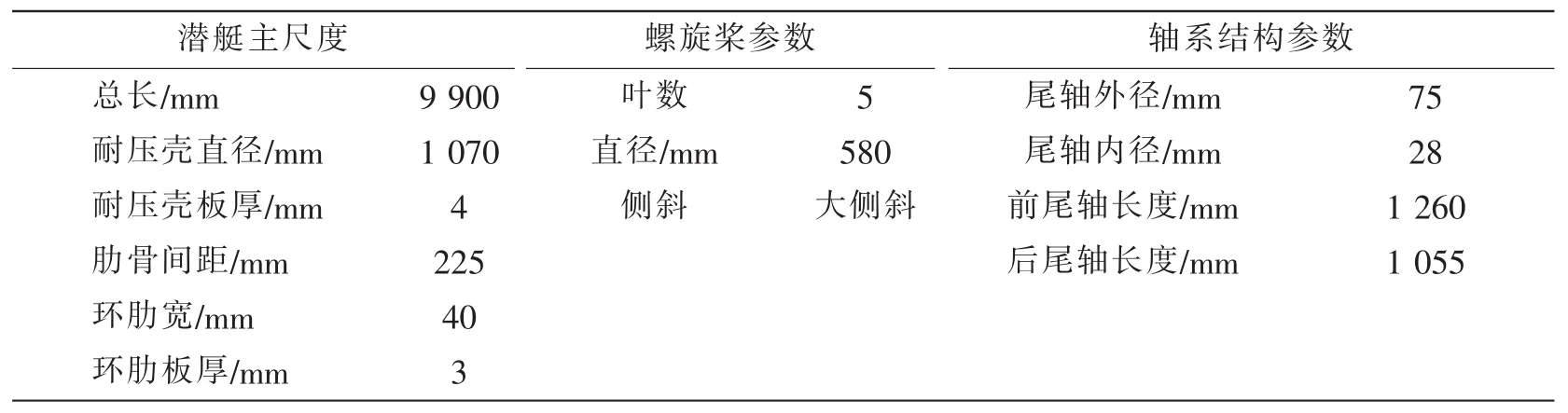
表1 SUBOFF潜艇模型的结构参数Tab.1 SUBOFF submarine structure parameters

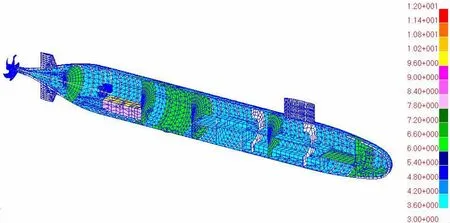
图1 SUBOFF整艇结构有限元模型Fig.1 FE model of SUBOFF submarine

图2 SUBOFF内部结构有限元模型Fig.2 Inner structures of SUBOFF submarine

图3 尾部轴系系统结构有限元模型Fig.3 Shafting system of SUBOFF submarine stern

图4 螺旋桨结构有限元模型Fig.4 Propeller structure

图1～4为SUBOFF模型艇的结构有限元模型，其中图1为SUBOFF模型艇的整艇结构有限元模型，潜艇结构左右对称，为了能清楚地表示内部板厚，这里只画出整个模型的左半部分，图2为内部结构有限元模型，图3为尾部轴系系统有限元模型，图4为螺旋桨结构有限元模型，图3中尾后轴承和尾前轴承用一维弹簧单元模拟，另外，本文只研究艇体在螺旋桨垂向激振力作用下的声学特性，激振力如图3所示。

1.2 结构—流体耦合方程

水下结构振动与辐射噪声问题是一个流体—结构相互作用的流固耦合问题。考虑如图5所示的结构—流体相互作用的系统：S0表示弹性薄壳结构，Ωo表示流体外域，流体外域充满密度为ρo的声介质，其声速为co，若系统进入稳态，角频率为ω，则波数ko=ω2/co。

对结构域采用有限元离散，对外域流体采用边界元法以获得附加质量和阻尼系数，将附加质量和附加阻尼叠加到结构有限元质量矩阵和阻尼矩阵上，建立了考虑流体耦合作用的有限元结构动力响应方程，如（1）式所示，从而实现流固耦合计算，进而使用边界元方法计算结构的辐射声场，

图5 流体—结构相互作用系统Fig.5 Fluid-structure interaction system

式中：KS为结构刚度矩阵，MS为结构质量矩阵，CS为结构阻尼矩阵，｝为节点位移向量，｝为直接作用在结构上的节点力，矩阵］即为外域流体对结构作用所产生的附加质量和附加阻尼矩阵。

一旦得到结构位移，可提取结构-外域流体交接面上的节点位移，从而得到物面法向位移向量，进一步计算声场声压。上述公式的具体推导过程参见文献[12]。

为提高流体部分的计算效率，将网格重叠算法用于结构流固耦合的计算中。网格重叠算法是在流固耦合的边界上不再使用有限元网格作为边界元网格，而是重新定义一套比有限元网络要粗得多的边界元网格，即在有限元网格上重叠了一套粗的边界元网格。在本文的计算频段内，由于声波波长远大于结构弯曲波振动的波长，因此，采用网格重叠算法是合适的。

1.3 噪声辐射能力衡量指标

为了衡量潜艇结构的噪声辐射能力，采用辐射声功率，湿表面均方法向速度二个指标作为主要衡量指标。

辐射声功率是声源机械效率中的有效部分，壳体表面的辐射声功率大小反映了壳体表面辐射声波的本领高低；壳体表面的均方法向速度反映了壳体在流场中的结构响应，同时也表征了声源振动的平均速度。它们分别定义如下：

辐射声功率：

相应可以定义声功率级、均方法向速度级：

2 潜艇简化模型分析

在用有限元法对潜艇模型进行声辐射特性分析之前，先对模型进行简化，初步估计结构振动响应谱峰频率变化规律。

图6 简化模型Fig.6 Simplified model

2.1 潜艇简化模型

如图6所示，分3步将图1所示模型简化为两自由度弹簧质量隔振系统：

第1步：将尾后轴承、尾前轴承、推力轴承对轴的垂向支撑作用分别用不同刚度的弹簧来简化，但是，尾前轴承、推力轴承的刚度远大于尾后轴承的刚度，船体简化为弹簧的支撑基座；

第2步：由于轴较长，将尾前轴承、推力轴承及两者之间的轴段并入船体结构，船体简化为尾后轴承的支撑基座；

第3步：忽略重力的作用，将螺旋桨、尾后轴承及两者附近的轴段简化为减振器，将第2步的整个模型简化为两自由度弹簧质量隔振系统，其中螺旋桨、艇体分别简化为质量块M、m，尾轴承垂向刚度为k，系统阻尼系数为分别为M与m的位移，是螺旋桨垂向激振力，其中f0是幅值，ω是圆频率。

对M、m可分别列出运动方程为：

式中：ω 是圆频率，单位是弧度/s，ω=2πf，频率 f的单位是 Hz，定义为M与弹簧组成的减振器的固有频率。

2.2 尾后轴承刚度对潜艇简化模型振动响应的影响

为了更加全面地了解尾后轴承刚度不同时对潜艇简化模型振动响应的影响，尾后轴承刚度k在1.0×105N/m和1.0×109N/m之间取值，k的取值及其相对应的固有频率fn如表2所示，其中，k取了5个不同值，分别用 k1、k2、k3、k4、k5 表示，且满足 k1＜k2＜k3＜k4＜k5， 简化模型中 M=44.0 kg、m=2.30×103kg。

根据公式（6）、公式（7）计算尾后轴承刚度不同时M位移幅值 A1、m位移幅值A2，A1、A2的最大值对应的频率，即谱峰频率随刚度增大的变化情况如表3所示。

由表3可以看出，A1、A2的谱峰频率随刚度增大而增大，而且刚度越大，相邻两个谱峰频率的差值越大，如表4所示。

表4结果表明，通过增大尾后轴承刚度，能够使谱峰频率迅速向高频移动。为了解释谱峰频率随刚度增大而增大的原因，将刚度不同时，谱峰频率和减振器固有频率列出，如表5所示。

由表5可以看出，谱峰频率出现在减振器固有频率处，因为fn随刚度k增大而增大，所以谱峰频率随刚度增大而增大是正确的。减振器的振动固有特性直接影响了M、m的振动特性。

表2 弹簧刚度和固有频率Tab.2 Spring stiffness and natural frequency

表3 弹簧刚度和谱峰频率Tab.3 Spring stiffness and spectral peak frequency

表4 两个谱峰频率的差值Tab.4 Difference of the two spectral peak frequencies

表5 谱峰频率与固有频率的比较Tab.5 Comparison between spectral peak frequency and natural frequency

表6 尾后轴承刚度Tab.6 Rear bearing stiffness

2.3 尾后轴承刚度对潜艇结构固有频率的影响

为研究方便，将图3所示的螺旋桨、尾后轴承及两者附近的轴段组成的系统称作轴系系统。

根据表5的结果，可以判断，尾后轴承刚度对轴系系统的固有频率及整艇结构固有频率必然有直接的影响，最终对潜艇振动响应谱峰频率有直接的影响。刚度取值如表6所示，且k1＜k2＜k3＜k4＜k5＜k6＜k7，刚度不同时，轴系系统整体弯曲振动一阶固有频率和振型如表7所示，振型为半波形，潜艇结构整艇弯曲振动一阶固有频率和振型如表8所示，振型为整艇半波形，低频振动表现的是梁式振动。

由表7-8可知，轴系系统整体弯曲振动一阶固有频率、整艇弯曲振动一阶固有频率随尾后轴承刚度增大而增大。

表7 轴系系统整体弯曲振动一阶固有频率与尾后轴承刚度之间的关系Tab.7 Relation between the first order natural frequency of the shafting system and the rear bearing stiffness

表8 整艇弯曲振动一阶固有频率与尾后轴承刚度之间的关系Tab.8 Relation between the first order natural frequency of the submarine structure and the rear bearing stiffness

续表8

3 潜艇模型在空气中的振动响应分析

改变尾后轴承刚度，研究潜艇结构在螺旋桨垂向力作用下振动响应谱峰频率、峰值变化规律，谱峰频率与潜艇结构弯曲振动固有频率之间的关系。

3.1 结构模型

结构模型如图1所示，在螺旋桨重心施加1 N垂向脉动激振力，计算尾后轴承刚度不同时潜艇结构的振动响应，并进行比较，刚度取值如表6所示。

3.2 结构在空气中的振动响应

采用NASTRAN有限元计算软件对潜艇结构在空气中的振动响应进行了计算，计算的频率范围是10-800 Hz，频率间隔是1 Hz。

在低频段，尾后轴承刚度不同时，整艇外表面的均方法向速度的频率曲线如图7所示。

图7 空气中整艇外表面的均方法向速度Fig.7 Mean square normal velocities of submarine outer surface in air

根据图7可以看出，谱峰频率变化特点如下：

（1）第一个谱峰频率随尾后轴承刚度增大而增大，增大的速度随刚度的增大而变慢，当刚度增大到一定值时，趋于不变。

（2）第二个谱峰频率随尾后轴承刚度增大而增大，增大的速度随刚度的增大而变慢，当刚度增大到一定值时，趋于不变。

下面对上述两个特点出现的原因进行逐个解释，首先解释第（1）个特点出现的原因。

将尾后轴承刚度不同时潜艇轴系系统弯曲振动一阶固有频率和潜艇振动响应第一个谱峰频率列出，如表9所示。

由表9可知，第一个谱峰频率出现在轴系系统整体弯曲振动一阶固有频率处，根据2.1节简化模型的减振器固有频率与质量块M、m振动响应谱峰频率的关系以及2.2节轴系系统整体弯曲振动一阶固有频率与尾后轴承刚度之间的关系可知，第一个谱峰频率随尾后轴承刚度的增大而向高频移动是正确的。

下面解释第（2）个特点出现的原因。

表9 轴系系统弯曲振动一阶固有频率和潜艇振动响应第一个谱峰频率的比较Tab.9 Comparison between the first order natural frequency of the shafting and the first spectral peak frequency of the submarine

表10 整艇结构弯曲振动一阶固有频率和振动响应第二个谱峰频率的比较Tab.10 Comparison between the first order natural frequency and the second spectral peak frequency for submarine

将尾后轴承刚度不同时潜艇整艇结构弯曲振动一阶固有频率和整艇结构振动响应第二个谱峰频率列出，如表10所示。

由表10可知，第二个谱峰频率出现在整艇弯曲振动一阶固有频率处，根据2.2节得出的尾后轴承刚度与整艇弯曲振动一阶固有频率之间的关系可知，第二个谱峰频率随尾后轴承刚度的增大而向高频移动是正确的。

第一、二个谱峰频率对应的峰值如表11所示。根据图7和表11可以看出，峰值变化特点如下：

（1）随尾后轴承刚度增大，第一个峰值先减小后增大，第二个峰值呈增大趋势；

（2）在经过第一个谱峰附近的窄频带之后，几乎在整个计算频段内，尾后轴承刚度越小，振动响应越小，减振效果明显。

综上可知，可以通过改变尾后轴承刚度来改变振动响应谱峰频率，选择合适的尾后轴承刚度可以达到减振的目的。

表11 空气中振动峰值Tab.11 Vibration peak value in air

4 潜艇结构水中振动和辐射噪声特性分析

研究随着尾后轴承刚度不同，辐射声功率，湿表面均方法向速度的谱峰频率、峰值变化规律，并且考察振动与辐射噪声之间的关系，以期望为低辐射噪声结构的设计提供理论指导。

计算模型同3.1节，采用结构有限元耦合流体边界元法对潜艇结构在水中的振动响应进行了计算，计算的频率范围是10-800 Hz，频率间隔是1 Hz。

4.1 结构湿表面均方法向速度变化规律

在低频段，尾后轴承刚度不同时，整艇湿表面均方法向速度的频率曲线如图8所示，第一、二个谱峰频率和峰值如表12所示。

图8 整艇水中湿表面的均方法向速度Fig.8 Mean square normal velocities of submarine wet surface under water

表12 潜艇结构水中振动响应谱峰频率和峰值Tab.12 Spectral peak frequency and peak value of vibration for submarine under water

根据表12和图8可以看出，谱峰频率、峰值变化特点如下：

（1）谱峰频率方面，第一、二个谱峰频率均随尾后轴承刚度增大而增大，且增大的速度随刚度的增大而变慢，当刚度增大到一定值时，趋于不变。

因此，可以通过改变尾后轴承刚度来改变振动响应谱峰频率。

（2）峰值方面，随尾后轴承刚度增大，总体上看，第一、二峰值均呈先增大后减小的趋势；在经过第一个谱峰附近的窄频带之后，几乎在整个计算频段内，尾后轴承刚度越小，振动响应越小，减振效果明显。

因此，选择合适的尾后轴承刚度可以达到减振的目的。

4.2 水中结构辐射声功率变化规律

在低频段，尾后轴承刚度不同时，整艇湿表面的辐射声功率的频率曲线如图9所示，第一、二个谱峰频率和峰值如表13所示。

表13 潜艇结构水中辐射声功率谱峰频率和峰值Tab.13 Spectral peak frequency and peak value of acoustic radiation power for submarine under water

根据表13和图9，可以看出谱峰频率、峰值变化特点如下：

（1）谱峰频率方面，第一、二个谱峰频率均随尾后轴承刚度增大而增大，且增大的速度随刚度的增大而变慢，当刚度增大到一定值时，趋于不变；

因此，可以通过改变尾后轴承刚度来改变辐射噪声谱峰频率。

（2）峰值方面，随尾后轴承刚度增大，总体上看，第一个峰值呈增大趋势，第二个峰值明显增大；在经过第一个谱峰附近的窄频带之后，几乎在整个计算频段内，尾后轴承刚度越小，辐射声功率越小，降噪效果明显。

因此，通过减小尾后轴承刚度可以达到降噪的目的。

根据表12～13，可以看出，在振动响应出现峰值的频率点，结构辐射声功率也会出现峰值，也就是说，当结构振动大时，辐射噪声的能力也强。

图9 整艇结构水中辐射声功率Fig.9 Acoustic radiation power for submarine under water

5 结 论

以SUBOFF潜艇为研究对象，通过改变尾后轴承刚度和振动传递路径的声学特性，根据结构振动和辐射噪声的计算结果，得到以下结论：

（1）在空气中，改变尾后轴承刚度，可以改变潜艇结构弯曲振动响应的谱峰频率和峰值，尤其是低频响应的谱峰频率和峰值；

（2）在水中，改变尾后轴承刚度，同样可以改变振动响应、辐射声功率的谱峰频率和峰值。在结构振动出现峰值的频率点，辐射声功率也会出现峰值，也就是说，结构振动大时，辐射声能的能力也强；

（3）在设计的时候，要根据实际的应用要求来选择合适的尾后轴承刚度，达到设计者的目的。

（4）与文献中的方法相比，本文提出的结构振动传递路径的声学设计方法同样能达到控制潜艇结构声学特性的目的，但却不需要在轴系上另加设备，而且适用于各种轴系，更具普适性。

[1]Dylejko P G,Kessissoglou N J.Optimization of a resonance changer to minimize the vibration transmission in marine vessels[J].Journal of Sound and Vibration,2007,300:101-116.

[2]曹贻鹏,张文平.使用动力吸振器降低轴系纵振引起的水下结构辐射噪声研究[J].哈尔滨工程大学学报,2007,28(7):747-751.Cao Yipeng,Zhang Wenping.Using dynamic absorbers to reduce underwater structural noise due to longitudinal vibration of shafting[J].Journal of Harbin Engineering University,2007,28(7):747-751.

[3]Merz S,Kessissoglou N J,Kinns R.Influence of resonance changer parameters on the radiated sound power of a submarine[J].Acoustics Australia,2009,37(1):12-17.

[4]Merz S,Kessissoglou N J,Kinns R.Minimisation of the sound power radiated by a submarine through optimization of its resonance changer[J].Journal of Sound and Vibration,2010:980-993.

[5]曹贻鹏.推进轴系引起的艇体结构振动与辐射噪声控制研究[D].哈尔滨:哈尔滨工程大学,2008:45-125.Cao Yipeng.Study on underwater structure vibration and radiated noise control caused by propeller exciting force[D].Harbin:Harbin Engineering University,2008:45-125.

[6]李攀硕,李栋梁,张志谊.轴—艇体系统耦合振动的建模与分析[J].振动与冲击,2012,31(5):128-131.Li Panshuo,Li Dongliang,Zhang Zhiyi.Modeling and analysis for coupled vibration of a shaft-hull system[J].Journal of Sound and Vibration,2012,31(5):128-131.

[7]Pan J,Farag N,Lin T.Propeller induced structural vibration through the thrust bearing[C]//Annual Conference of the Australian Acoustical Society.Adelaide,Australia,2002:390-399.

[8]Cao Y P,Zhang W P.Research on methods of reducing underwater structure acoustic radiation caused by longitudinal vibration of shafting[C]//Asian Link EAMAREVT,2007.Harbin,China,2007.

[9]谢基榕,徐利刚,沈顺根.推进器激励船舶振动辐射声计算方法[J].船舶力学,2011,15(5):563-569.Xie Jirong,Xü Ligang,Shen Shungen.Calculational method for radiating sound excited by vibration of ship propeller[J].Journal of Ship Mechanics,2011,15(5):563-569.

[10]谢基榕,沈顺根,吴有生.推进器激励的艇体辐射噪声及控制技术研究现状[J].中国造船,2010,51(4):234-241.Xie Jirong,Shen Shungen,Wu Yousheng.Research status on noise radiation from vibrating hull induced by propeller and reduction measures[J].Shipbuilding of China,2010,51(4):234-241.

[11]Nancy C G,Hthomas T H,Ming S C.Geometrics characteristics of DARPA SUBOFF models[R].Bethesda:David Taylor Research Center,1989.

[12]Zhou Qidou,Joseph P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J].Journal of Sound and Vibration,2005,283:853-873.