争·鸣——一个基于核心素养的教学与评价案例

段艳芳

（太原市实验中学，山西 太原）

《普通高中数学课程标准（2017年版）》中指出，要关注学生个性化、多样化的学习和发展需求，促进人才培养模式的转变，着力发展学生的核心素养.教学实践中，如何在学生掌握知识技能的同时，促进数学学科核心素养的提升及水平的提高，是一个前景光明而道路曲折的研究课题，而下面这则案例，就是漫漫长路中的一次微小的尝试与探索。

【案例描述】

在必修二（人教A版）的第2.3.1节直线与平面垂直判定定理的学习中，我设置了一个折纸探究的小试验，希望学生能够通过动手操作来直观感知：如何判断一条直线与已知平面是否垂直。

师：请同学们将手中的三角形纸片进行翻折，得到一条折痕，再把翻折后的纸片竖起放置在桌面上，然后思考两个问题：

1.折痕与桌面垂直吗？

2.怎样翻折才能使折痕与桌面垂直？

一番讨论探究后，学生们开始展示。

A组：当折痕是三角形BC边上的高线时，与桌面垂直。

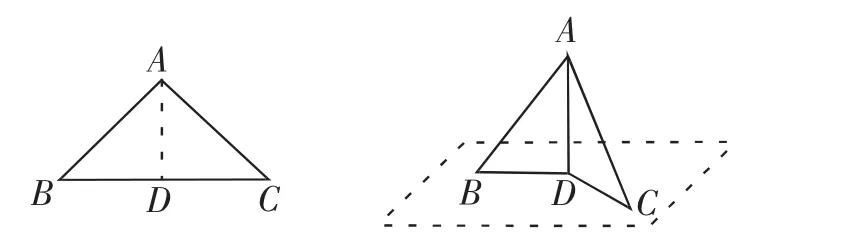
这是我所预设的结果，也是教材上的规范回答，一切进行得很顺利，接下来就可以导入新课了，我微笑着例行公事地又问了一句：“他说的对吗？有没有其他意见？”

这时，有个声音从后排传来：“我们组折的不是高线，好像也垂直。”声音中带着太多的不确定，但全班同学都听到了，大家不约而同地把目光投向他桌上竖立着的一个硕大的折过的三角形，果然折痕不是高线，我仔细看看F组的作品，问组长：“你们组为什么觉得这样也垂直？”

“这样折它能站在桌面上，要是折成别的样子就站不稳。”组长指指桌子上摆着的另外几个站得歪歪斜斜的三角形作品，回答道。

如此感性而离谱的回答，让我很想叹气，但还是继续问道，“这是谁的原创？”旁边的小G嗖地站起来，“我折的，照着我家阁楼上墙角的样子折的。”居然还有他家阁楼的戏，全班哄堂大笑，一时间班里学生有的赞同有的反对，议论纷纷，说个不停。

讨论片刻后，向来寡言的小E主动站起来说，“我觉得这两种折法都对，看起来都像老师刚才举例时提到过的旗杆与地面的关系。”

随即，小G将那个硕大的三角形高高举起，得意地炫耀，“就是，都看着啊，我的折痕和你们的是平行的，嗯，平行的不就是一样的？”他思路有点含糊，但是抓住了问题的关键。

我立即顺水推舟，“两条平行的折痕，它们都和桌面垂直吗？请大家参阅课本，来解开这个谜底。”

教室里沉静下来，一种思维的张力在弥漫，我耐心地等待着，等待着……

不久，学生开始兴奋地发表高见，“是否站得住不是是否垂直的理由！”

“平行!折痕是平行的，两种折痕都和底边垂直。”

“折痕只需要与底边垂直即可，高线可以，小G折得也正确。”“两平行直线应该垂直于同一平面。”

“为什么与底边垂直的折痕就与桌面所在平面垂直呢？”

“为什么直线与平面内的两条相交直线垂直，就可以垂直于该平面呢？”

学生的思维像海浪一样一波波地涌动……

【案例反思】

参照数学学科核心素养的水平划分，我欣喜地尝试着给学生在本堂课的学习状态与过程进行评价：

在探究线面垂直条件的过程中，学生能够通过观察旗杆与地面或者阁楼墙角等实例，直观想象，自行构建线面垂直的折纸实例，即能够在关联的情境中发现线面垂直要素，并且进行操作确认，完成了这个过程，根据满意原则，说明学生达到直观想象素养水平一的要求。

在出现折痕分歧时，学生抓住折痕平行这个特征进行探索分析逻辑推理，在交流的过程中，能够围绕主题，观点明确，论述有理有据，根据满意原则，可以认为达到逻辑推理素养水平二的要求。

在阅读课本，得到对于相关问题“知其然不知其所以然”的解答后，某些同学依然锲而不舍地试图探索线面垂直判定定理成立的缘由，说明对于新的数学问题，能够透过与折叠后底边垂直的表象，借助直观想象去探索问题的本质，寻求论证的途径，并且试图用严谨准确的数学语言来予以表达，能够完成这个过程，根据加分原则，可以认为这些同学达到数学抽象素养水平二的要求。

对于这堂课，我思绪万千，感触最深的是：充满学生思维的课堂才是真正的课堂。

如果强行用教师的想法代替学生的想法，用教师的思维控制学生的思维，这样的课堂只能越来越失去生命力。如果在课堂教学中我们尽可能多地把思考时间留给学生，使得学生保持旺盛的探究热情，充分激发他们的创造潜能，那么，学生就有可能在探究中闪耀出智慧的火花，在潜移默化中逐步提升数学学科素养。