智能仓库中的多机器人协同路径规划方法

张丹露，孙小勇，傅 顺，郑 彬+

(1.中国科学院大学 计算机控制学院，北京 101400；2.中国科学院 重庆绿色智能技术研究所，重庆 400714； 3.重庆德领科技有限公司，重庆 400714)

0 引言

随着电商行业与工业自动化的飞速发展，人们对高效的智能自动化仓储系统的需求越来越迫切，智能仓储系统成为智能系统研究领域的热点之一[1-3]。智能机器人是目前及未来机器人领域的研究热点，因此基于多移动智能机器人的自动化仓储系统也成为智能仓储系统的研究热点。许多企业，如亚马逊[4-5]、海康威视[6]等正在加速研究、布局基于多移动机器人的智能仓储系统。

多机器人间的协同路径规划和避障是实现基于多移动机器人的智能仓库的关键[7]，本文将通过预约表与交通规则下改进的A*算法和动态加权地图来解决上述问题，从而构建一个安全、稳定、灵活和可重构的智能仓库系统，并通过减少多机器人系统的运行时间来提高智能仓库系统的效率。

目前，多机器人系统主要的控制方法包括集中式控制方法和分布式控制方法。集中控制方法[8-9]由中央控制系统统一处理机器人间的碰撞协调问题，并为机器人找到一个全局最优路径，该方法安全稳定并且容易实现，已被广泛用于许多生产环境中。然而，随着仓库中央控制系统控制的机器人数目的增长，集中控制方法的计算复杂度将大幅提升而效率却逐渐降低。分布式控制方法[10-11]则是一种机器人利用自己获得的实时信息为自己进行路径规划的方法，采用该方法进行路径规划能适应快速增长的机器人数目和快速变化的仓库环境，比集中式控制方法更具扩展性与灵活性。然而，由于获得的信息有限，分布式控制方法只能为机器人找到局部最优路径，并且可能使机器人间发生碰撞、交通堵塞和死锁等问题。本文结合集中式控制方法和分布控制方法的优点，一方面通过集中式控制方式获得仓库的全局信息(如机器人的状态、位置等信息)，并利用全局信息构建预约表和动态加权地图，为机器人实时提供智能仓库中的交通信息；另一方面，机器人系统采用分布式控制方式，每个机器人根据中央控制系统提供的信息自行进行路径规划，既减少了中央控制系统的负担，又为多机器人路径规划提供了全局信息，使机器人能更加动态地规划路径。

由于仓库环境属于结构化环境，本文使用栅格地图[12-13]表示仓库环境。目前，机器人路径规划算法主要有A*算法[14-15]、D*算法[16-17]、蚁群算法等[18-19]。D*算法和蚁群算法均属于动态路径规划算法，可以避开未知的障碍，但是无法找到全局最优路径。并且智能仓库是由其他移动机器人和货物组成的障碍物多且快速变化的高度动态的环境，随着机器人数目的增多，上述动态规划算法潜在的问题也会随之出现，如交通堵塞和路径规划中的震荡，因此上述两种算法不是解决智能仓库多机器人动态路径规划的首选。A*算法是启发式搜索算法，该算法简单高效，能为机器人找到全局最优路径，是目前机器人路径规划中流行的算法。但是，由于多机器人工作在一个高度动态的环境中，A*算法可能会造成死锁。因此，本文采用交通规则[20-21]尽量避免碰撞和死锁，同时使用预约表记录栅格地图中每个栅格的状态。当机器人想进入一个栅格时，会查询预约表中当前时刻下的栅格状态，若该栅格状态为不可到达，则机器人将等待直到栅格状态变为可到达。结合交通规则和预约表的A*算法可以实现没有碰撞与死锁的机器人协同路径规划。

结合交通规则和预约表的A*算法可以解决碰撞和死锁问题，但是多机器人系统依然存在交通阻塞的问题。为了解决这一问题，Digani等[22]使用分层地图的方法。分层地图中的第一层地图为拓扑结构地图，将智能仓库进行分区，每一个区域为拓扑结构中的一个节点，区域中的机器人数目决定了拓扑结构中边的权重，机器人使用D*算法，根据拓扑结构中每条边的权重进行动态路径规划。分层地图的第二层是每个人为分割的仓库区域，人为分割的区域由栅格地图表示。机器人到达某一区域后将采用A*算法进行具体的路径规划，该方法可以在一定程度上实现多机器人的动态路径规划。然而，由于智能仓库被人为地划分为两层地图，机器人需要根据每层地图使用相应的路径规划方法，A*算法应用在高动态环境中会大大降低系统效率，并且分层地图是被人为划分的，存在不能精准反映交通拥堵区域的问题，不能满足智能仓库灵活性的需求。本文根据分层地图的优点提出动态加权地图，根据仓库中每个货架区域间的交通情况实时更新地图中每条边的权重。机器人利用改进的A*算法，根据每条边的权重计算路径代价，规划出一条更优的路径。通过改进的A*算法与动态加权地图就能够避免交通堵塞、减少多机器人系统的运行时间。

1 智能仓库模型及任务分析

本章提出一个利用率高、可重构的智能仓库模型，介绍一些将在智能仓库中用到的名词定义，然后分析多移动机器人在智能仓库中执行任务的流程。

这里采用文献[4-5]提到的智能仓库模型,该模型能充分利用仓库空间，并提供一个灵活的、可重构的环境，如图1所示。图中用栅格地图表示智能仓库环境，栅格地图被分为3部分：①位于栅格地图左侧的拣选台S={s1,…,sm}(m为拣选台的个数)，工作人员在拣选台进行打包工作，拣选台位于仓库边缘更方便货物的配送；②栅格地图中由相邻栅格连续构成的路径，为了充分利用仓库，货架间的路径都只允许一台机器人通过，即为单行道，并且两条交叉的路径形成了一个十字路口；③由货架L={l1,…,le}(e为货架个数)构成的货架区域，每个货架区由两条横向的道路和两条纵向的道路包围。一群机器人R={r1,…,rn}(n为机器人的个数)以统一的速度vri在仓库中行走并搬运货物。

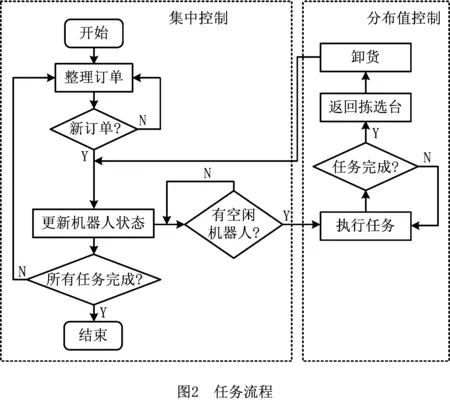
多机器人在智能仓库搬运货物的过程如图2所示。首先，中央处理系统处理货物订单，按照订单的时间、位置、种类等信息将订单进行分组,文献[23-26]详细介绍了不同的订单处理方法。本文主要研究多机器人的路径规划方法，因此只将订单按照多机器人离拣选台的距离进行分类排序。中央控制系统陆续将已经整理好的订单信息发送到对应的拣选台，拣选台sj(1≤j≤m)查看所有机器人的状态是否可用，若有空闲机器人，则选择离货物位置最近的一个机器人ri(1≤i≤n)执行订单任务。机器人得到一组订单任务后，依次根据订单中不同货物对应的位置信息进行路径规划，直到订单中的所有货物收集完毕，机器人ri携带所有货物返回拣选台sj。拣选台的工作人员对货物进行打包，机器人的状态则由工作中变为空闲，等待新的任务。

2 改进的A*算法与预约表

2.1 交通规则下与预约表

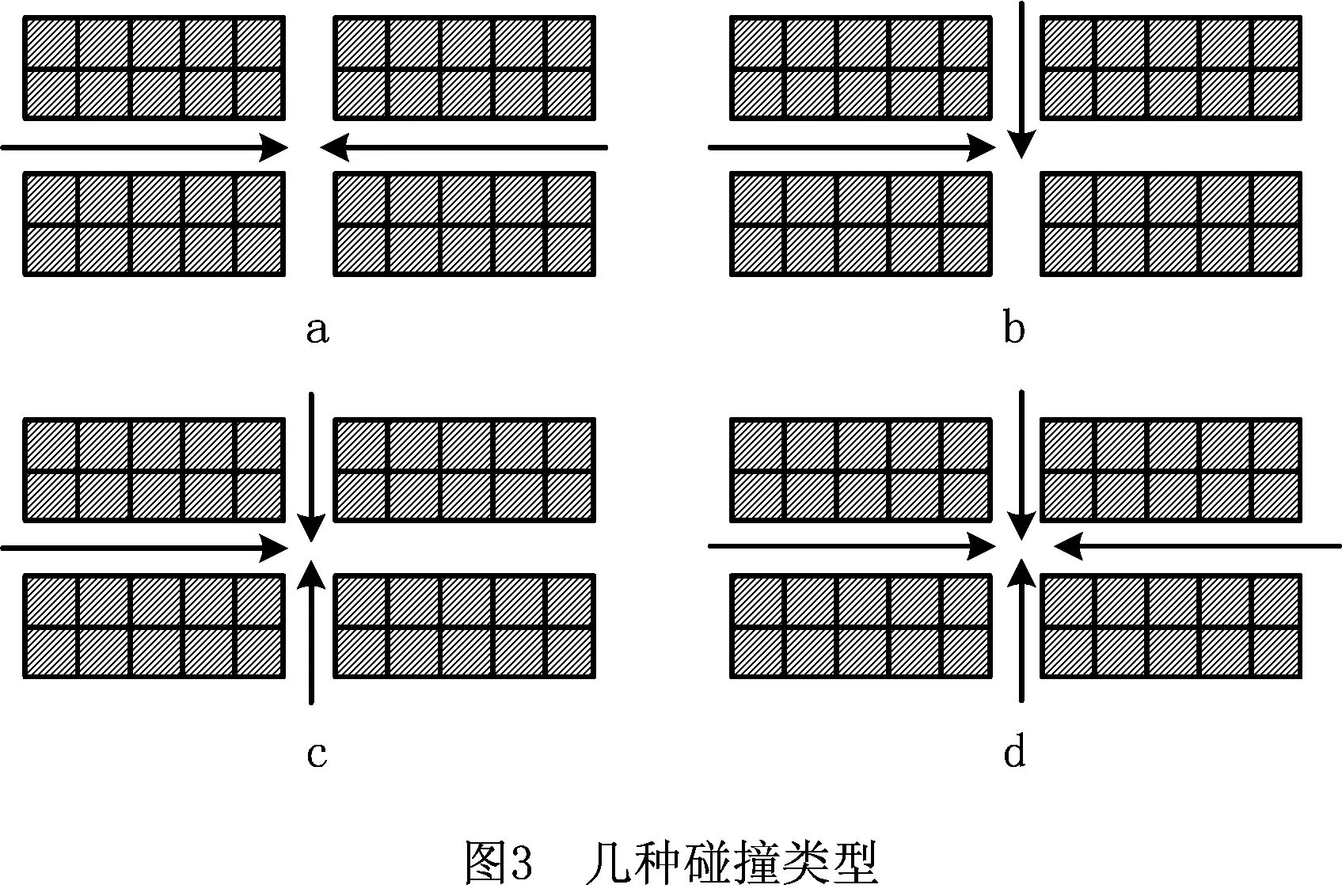
若一组在快速变换的动态环境中持续运行的机器人出现碰撞、堵塞甚至死锁问题，只使用动态路径规划算法并不能完全解决上述问题。图3所示为4种典型的碰撞情况，多个机器人在同一个地方碰撞时，会出现堵塞甚至死锁。如果碰撞属于情况b，则机器人可以通过等待其他权重更高的机器人先通过来解决。当出现其他3种碰撞情况时，机器人间的避让将花费大量时间，并且随着机器人数目的增多，碰撞和避让会造成死锁，可以通过使用交通规则来避免上述3种情况。规定仓库中货架之间的每条道路都是单行道，而且相邻两条道路的方向相反，机器人在仓库中行走时，只能沿着道路方向单向前进，从而在很大程度上避免碰撞和死锁。

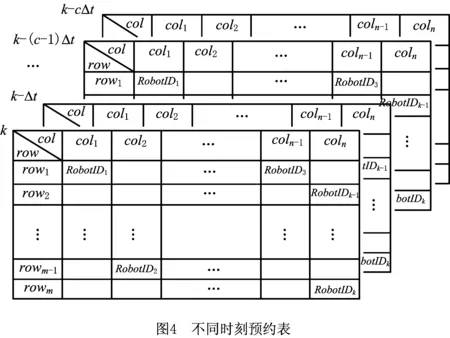
即使使用交通规则，机器人间仍然会存在碰撞，如图3b所示。因此，栅格地图中的每一个栅格在某一时刻只能被一个机器人占有。如果机器人准备进入的栅格被占用，则必须等到该栅格变为空闲，本文使用预约表记录栅格地图中每个栅格的状态。图4所示为从当前时刻t到之前一段时间内不同时刻更新的预约表，每隔一段时间Δt，中央控制系统将更新一次预约表，并存储之前一定时间内的预约表。预约表是一个大小同栅格地图一样的二维表格，表格中的空格记录着相应栅格地图中每个栅格的使用情况。如果栅格被占用，则表格中相应的位置会记录占用栅格的机器人的ID，其他机器人可以通过查询当前时刻的预约表来决定继续向前移动还是等待另一个机器人通过。如果多个机器人同时占用一个栅格，则将根据权重决定其占用顺序。较早出发的机器人拥有较高的权重，如果多个机器人拥有相同的权重，则随机决定占用栅格的顺序。

2.2 改进的A*算法

A*算法被称为最佳优先启发式算法，它比未知的探索算法更简单快速。算法步骤如下：从开始栅格出发，机器人每次选择下一步将要扩展的栅格时，都会估算与自己所在栅格相邻的栅格路径代价。路径代价指机器人从起始栅格出发，经过将要扩展的栅格，到达目标栅格的最短估算值。得到周围栅格的估算代价后，将其放入一个带扩展节点候选表格，然后在表格中选择一个估算代价最小的栅格进行扩展。机器人重复上述步骤，直到扩展到目标栅格。每个栅格的估算代价为

f*(n)=g(n)+h*(n)。

(1)

式中：g(n)为机器人从起始栅格移动到当前栅格n的真实代价，

(2)

vri为机器人ri匀速行驶的速度，d为机器人从起始栅格到当前栅格n的真实距离；

h*(n)为启发式方程，计算机器人从当前栅格n移动到目标栅格的估算代价，

(3)

dn为机器人从当前栅格n移动到目标栅格的最短估算距离，即曼哈顿距离，

dn=abs(n.x-goal.x)+abs(n.y-goal.y)，

(4)

n.x和n.y为当前节点在栅格地图中的横列和纵列，goal.x和goal.y为目标栅格的横列和纵列。

可以用距离、时间、权重等因素来估算f*(n)。传统A*算法主要用曼哈顿距离、欧拉距离等作为式(1)中估算函数的代价，本文用时间作为估算代价。

机器人根据智能仓库中的交通规则有序移动。如图5所示，横向箭头表示机器人只能按照交通规则从左向右移动，纵向箭头表示两条方向相反的单行道。横向道路由相邻栅格连接组成，栅格从n1～n17依次编号，如果机器人从栅格n1出发移动到目标栅格n17，则依次扩展栅格n2～n16。在智能仓库移动的机器人必须遵守仓库的交通规则，只要在栅格n6和n12处决定行驶方向，就能选择一条最佳路径。综上所述，为了简化机器人路径规划的步骤，提高整个机器人系统的路径规划效率，某些时候可以只在十字路口扩展节点。机器人在路径规划时有3种状态：

(1)从某一非十字路口栅格向十字路口栅格扩展。

(2)从十字路口栅格扩展到另一个十字路口栅格。

(3)从十字路口栅格扩展到目标栅格。

如果机器人在路径规划时处于状态(1)或状态(3)，则必须计算每个栅格的估算代价f*(n)来确定下一个要扩展的节点；如果机器人处于状态(2)，则只在十字路口栅格进行扩展，机器人在十字路口栅格确定方向和路线后，将按照确定的方向自动将上下一个十字路口之前的栅格加入候选节点扩展列表，并移动一定的栅格数，直到到达下一个十字路口。

如图6所示，从相同的起始栅格出发，机器人可以选择几条不同的路径到达相同的目标栅格，分别称为路径1、路径2、路径3，在结构化的智能仓库中，这3条路径的长度相同，传统的A*算法会随机选择一条路径进行扩展。然而，在真实的仓库环境中，机器人会在转角处花费更多的时间用于转弯，因此当机器人沿着相同路径长度的不同路径行走时会花费不同的时间。如图6所示，机器人沿路径1行走时有一次转弯，沿路径2行走时有3次转弯，沿路径3行走时有5次转弯，因此本文提出了转弯代价时间tturn。当机器人决定在十字路口转弯时，将tturn加入估算函数，式(1)被修改为

(5)

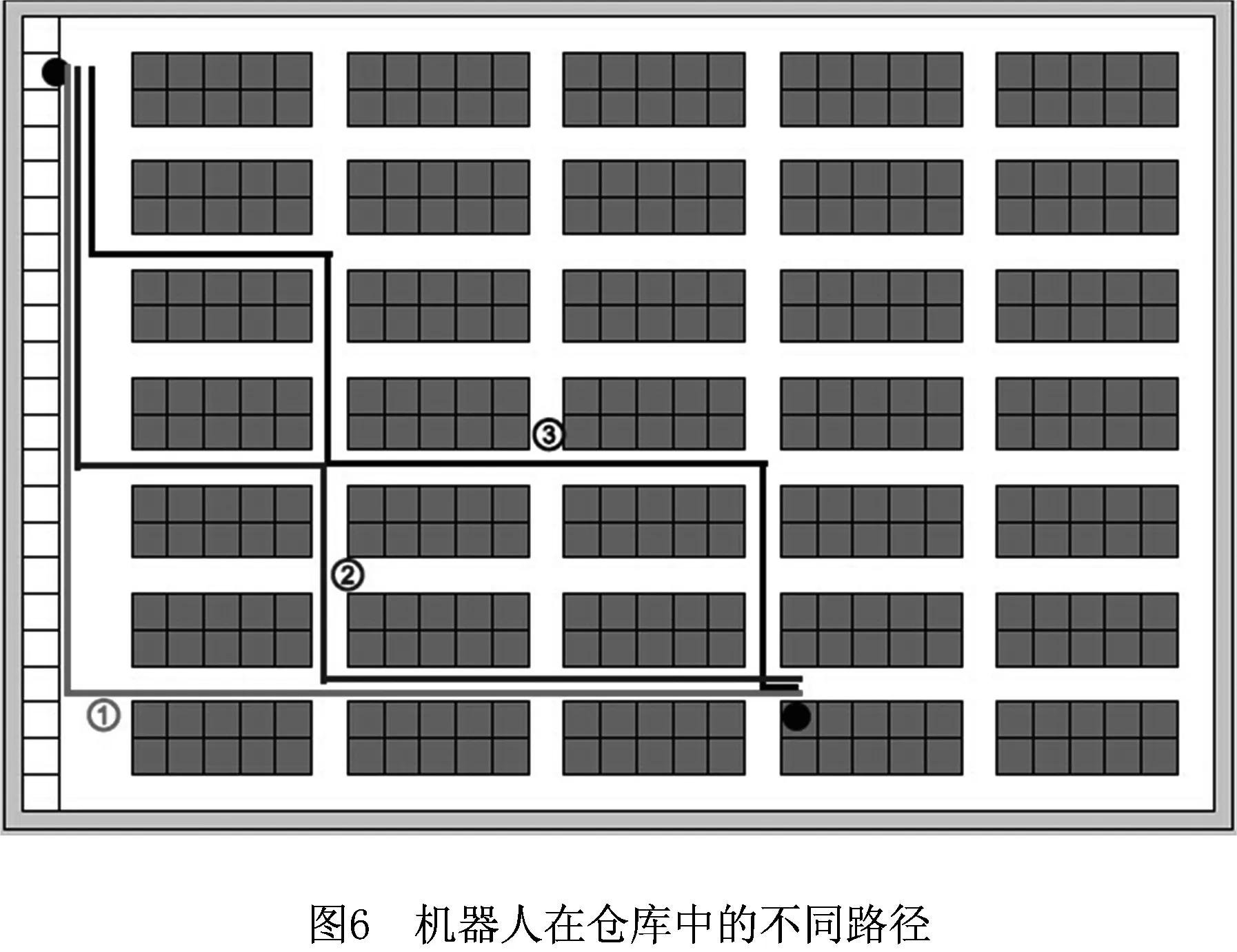
使用上述两种改进方法，可以选择一条路程更短耗时更少的路径，从而提高单个机器人路径规划的效率。

3 动态加权地图

上面提到的改进A*算法能解决机器人间的碰撞和死锁问题，提高单个机器人路径规划效率。但是，随着机器人数量的增加，所出现的交通堵塞问题将大大降低机器人系统运送货物的效率。本章通过动态加权地图来解决交通阻塞问题，提高整个机器人系统的效率。

图7所示为栅格地图和动态加权地图，图中每个节点表示一个十字路口，两个节点之间的边表示十字路口之间的路径。连接两个节点的路径和路径两旁的货架组成两个节点间的货架区域，每两个节点间的货架区域和拣选台组成整个智能仓库。动态加权地图中的每条边表示一个相邻节点间的货架区域，每条边的权重随着货架区域拥塞程度的变化而变化，机器人可以根据权重动态规划路径来避让交通堵塞区域。

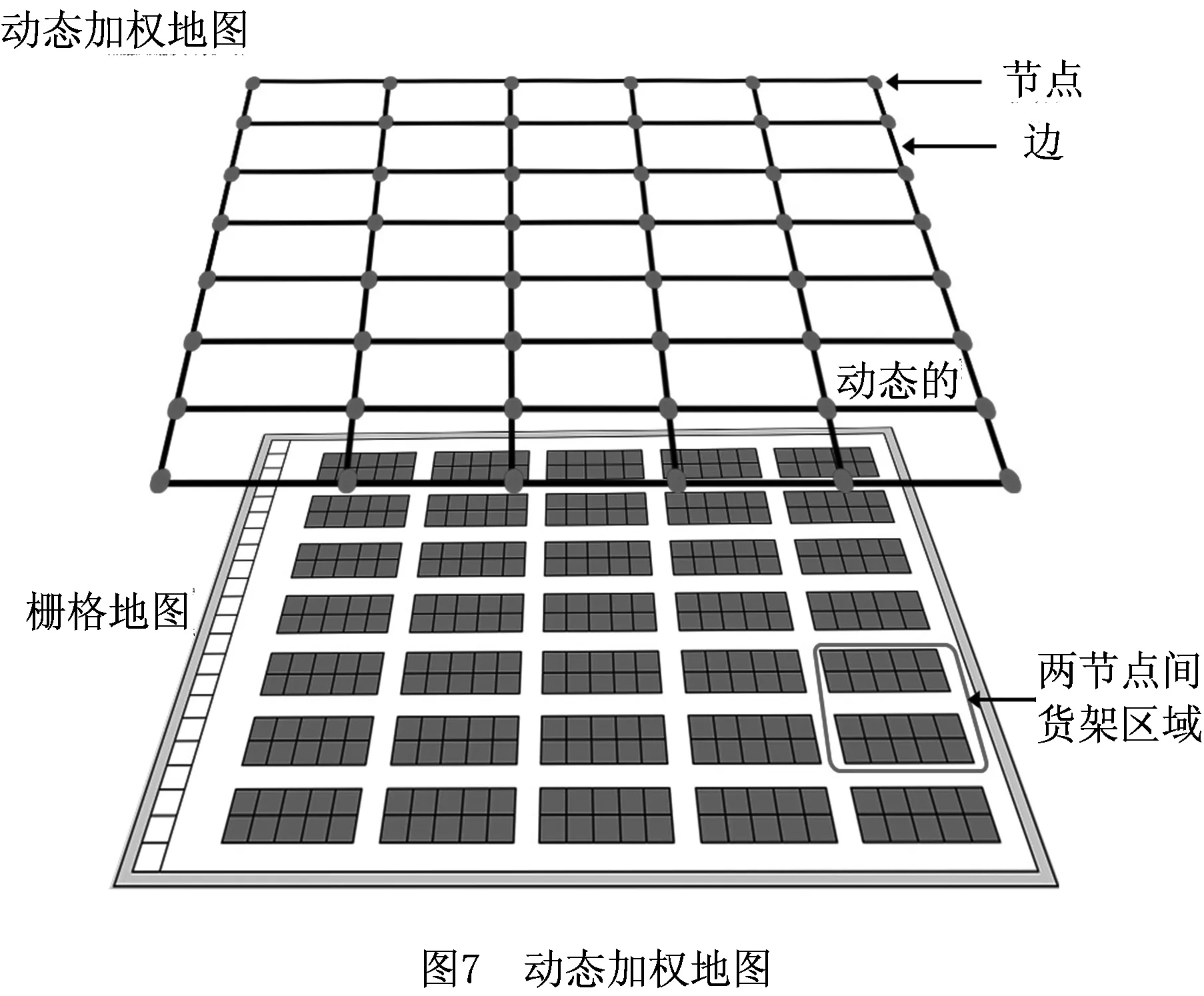
每隔一定时间Δt，中央控制系统更新一次预约表，预约表中存储了某一时刻每个机器人在仓库中的位置信息，而中央控制系统则存储了从k时刻开始之前一段时间c·Δt内更新过的预约表(c表示更新次数)。机器人在k时刻到达十字路口时，通过中央控制系统获得k-c·Δt～k时刻将要进入的货架区域内其他机器人的位置信息，通过对比该时间段内其他机器人在货架区域内的位置信息获得该区域内的交通堵塞情况。权重计算公式为

(6)

若机器人在某一货架区域内出现故障不能移动，则N的值为无穷大，否则为1。Nestimate(k-c·Δt,k)表示在交通顺畅的情况下，从k-c·Δt～k时刻，货架区域应该通过的机器人数量的估算值。首先机器人得到k-c·Δt时刻该货架区域内其他机器人的位置信息，估算经过时间c·Δt后在k-c·Δt时刻该区域的机器人应该通过的数目；然后机器人得到k-(c-1)·Δt时刻该货架区域内新进入的其他机器人的位置信息，估算经过时间(c-1)·Δt后，从k-(c-1)·Δt时刻以后进入该区域的机器人应该通过的数目，以此类推，直到估算k-Δt～k时刻应该通过的机器人数目；最后，每个时间段估算值的总和为k-c·Δt～k时刻货架区域应该通过的机器人数量的估算值。Nreal(k-c·Δt,k)表示k-c·Δt～k时刻，该货架区域内的真实通过的机器人数目，当Nreal(k-c·Δt,k)=0且Nestimate(k-c·Δt,k)≠0时，估算值wdynamic为无穷大。

机器人先通过栅格地图和改进A*算法进行路径规划。机器人每进入一个十字路口均需查看最新的动态加权地图。如果预计通过货架区域在地图中对应边的权重为0或1，则表示该区域没有交通堵塞，可以继续通过该区域；否则，机器人将利用动态加权地图估算通过该区域的额外时间：

textra=wdynamic·twait。

(7)

式中twait表示机器人为了等待另一个机器人通过而执行停止、等待、启动这一过程所花费的时间。机器人在十字路口使用如下方程重新进行路径规划：

f′*(n)=g(n)+h′*(n)+∑tturn。

(8)

式中h′*(n)表示机器人遇到交通阻塞时使用的一个新的估算函数，它结合了A*算法中基本的估算值和动态加权地图中动态估算值，

(9)

4 仿真实验

本章采用MATLAB进行仿真实验。利用图1提出的仓库模型，将本文提出的动路径规划方法与目前机器人路径规划中普遍使用的交通规则下的A*算法进行比较，证明动态加权地图下改进的A*算法能有效提高多机器人系统在智能仓库中的运行效率。仿真实施情况如下：

(1)对比不同机器人数量执行相同任务的情况，机器人数依次为10,20,30,40,50。

(2)不同数目的机器人系统依次执行获取300个货物的订单，每个货物订单分为50组，每组6个货物任务。货物订单随机产生，且随机产生5个订单，每组机器人分别执行5个订单任务，最后获得完成任务的总时间和总路程的平均值。

(3)对比相同数目机器人系统使用两种不同路径规划方法执行货物数目不同的订单的情况，并获取平均值。货物数目依次为300,360,420,480,540,600

(4)相同数目的机器人执行相同任务时，将使用两种不同的路径规划方法，简称为算法1(动态加权地图下改进的A*算法)和算法2(交通规则下的A*算法)。

如图8所示，箭头所指的黑色空心圆表示一个移动机器人r1，黑色实心圆表示机器人系统中的其他机器人，它们在仓库中协同搬运货物。r1从拣选台区域的黑色方块处出发，目标是到达货架区域的黑色方块处获取货物。图9所示为动态加权地图，黑色区域表示仓库中的货架位置，白色区域表示可通行的仓库通道区域，仓库通道区域中的灰色部分表示道路中存在的拥堵区域，灰度越深表示拥堵情况越严重。由图9可见，在某一时间段，由于机器人集中在某些区域搬运货物，机器人r1在图8所示的黑色矩形方框处遇到了拥堵。如图10仓库路径中的灰色区域所示，机器人采用算法2会选择能到达目标货物的最短路径，但是却要在拥堵区域等待一段时间，造成资源浪费。如图11中仓库路径中的灰色区域所示，机器人采用算法1根据动态加权地图显示的拥堵情况，通过花费一定的路径代价选择了一条用时更少的路径，节省了取货时间。

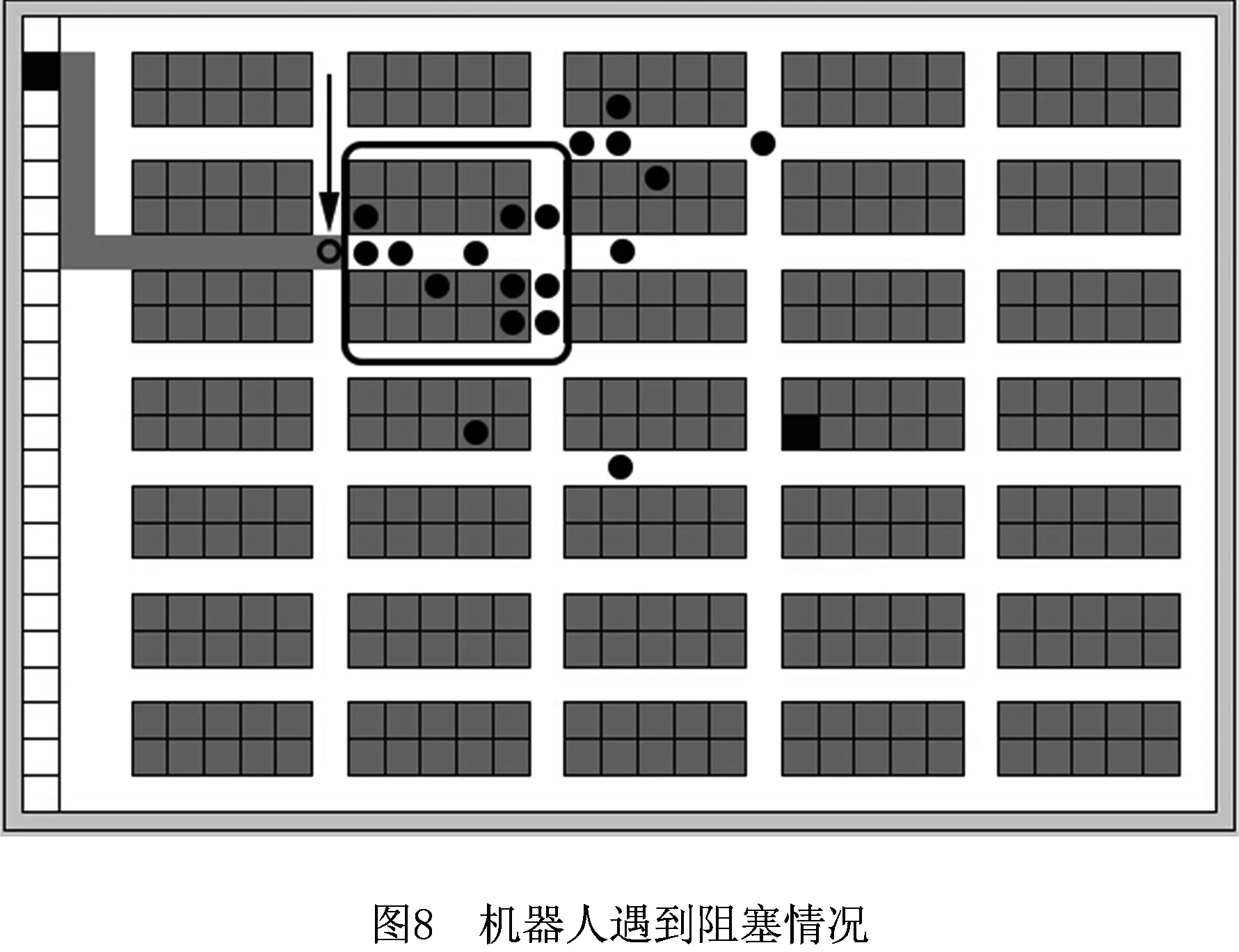
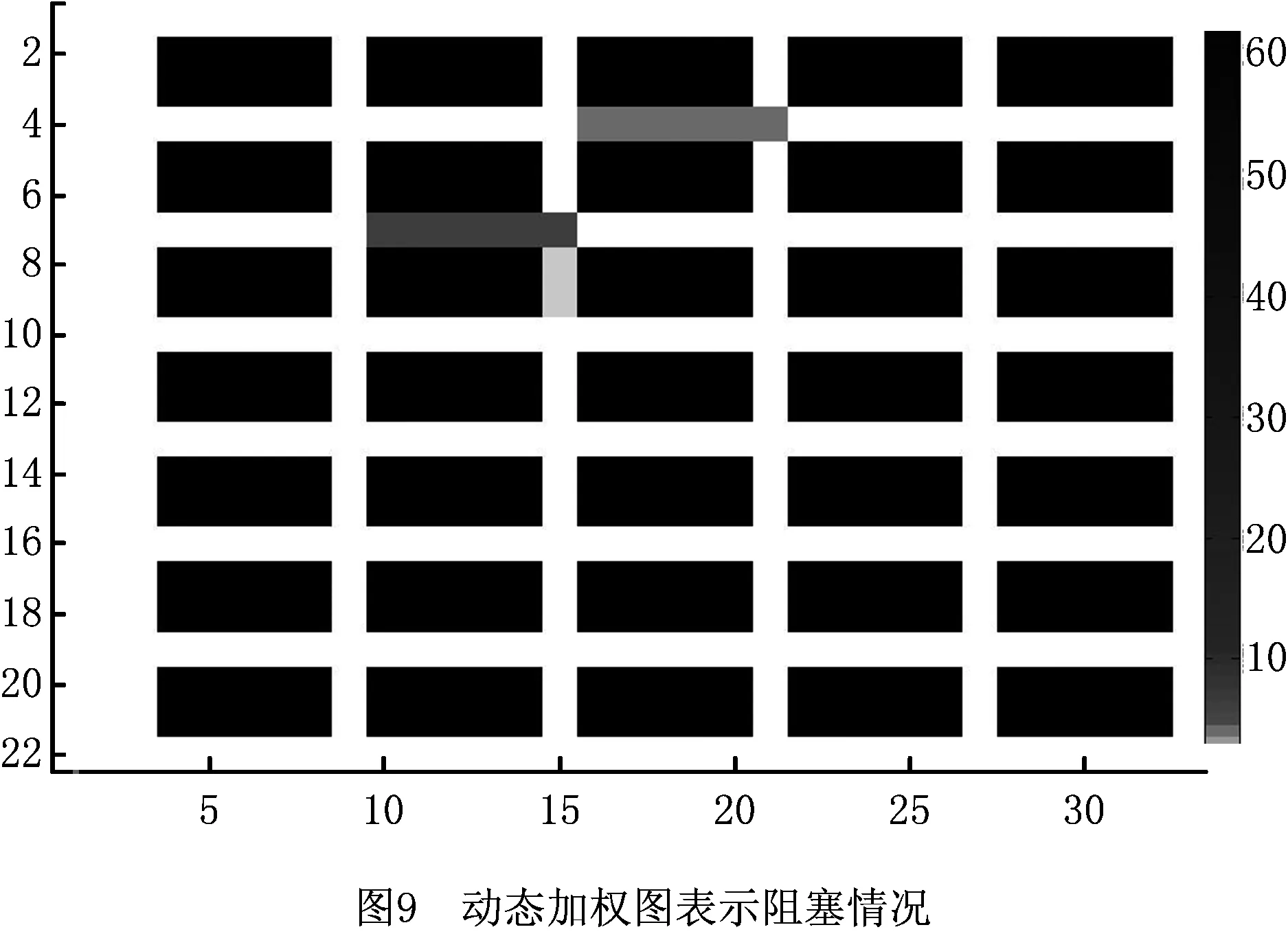
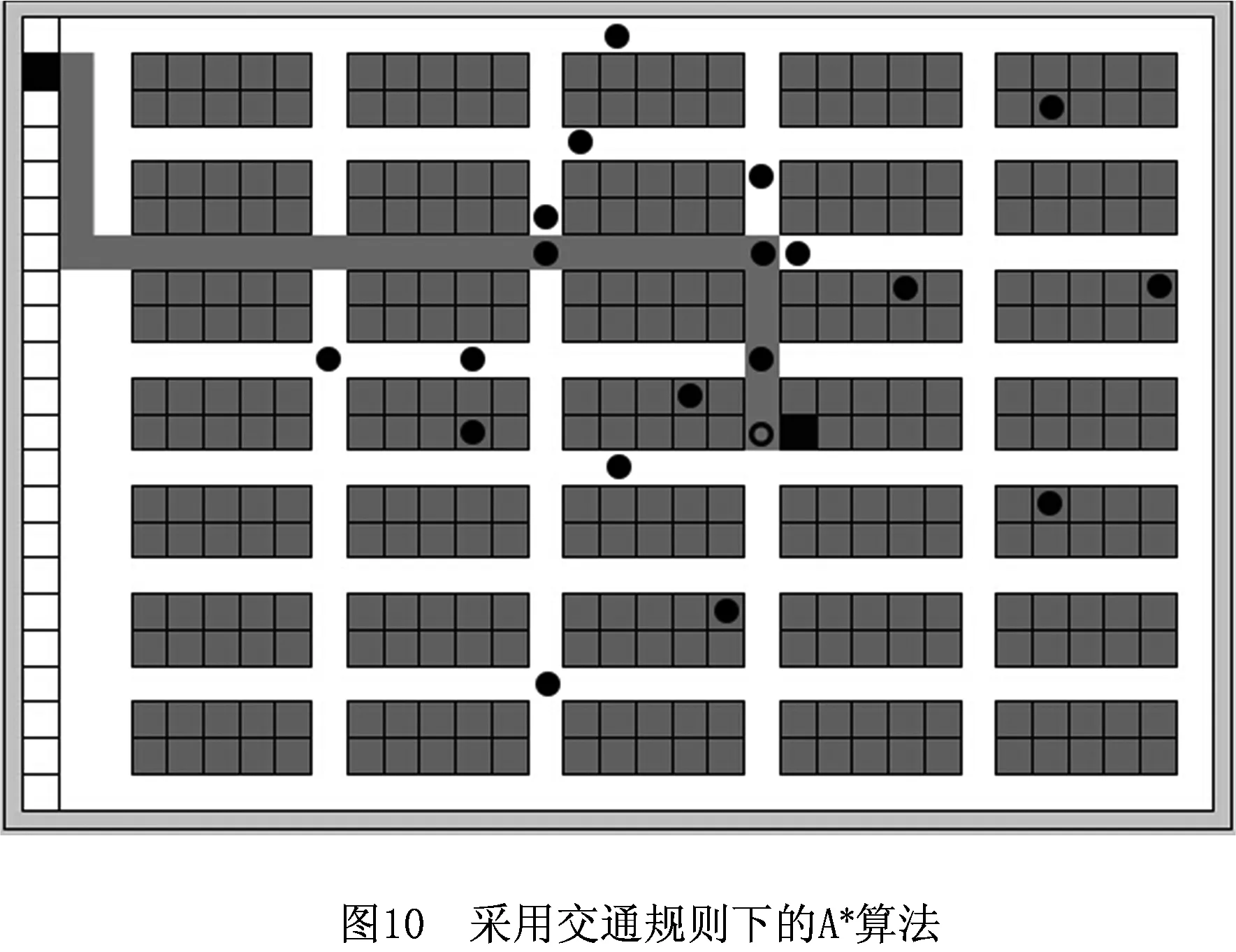
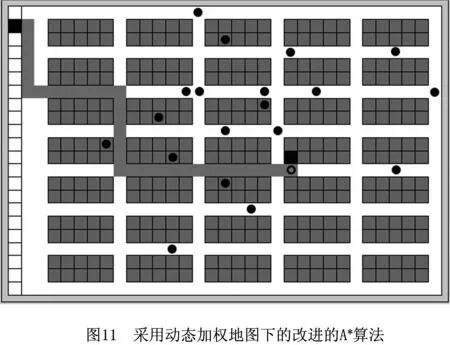
图12所示为使用不同数目机器人的多机器人系统在使用不同路径规划算法后，搬运300个货物所花费的总时间。总的来说，机器人系统完成任务所需的时间随着机器人数目的增多而减少。相对于算法2,使用算法1能有效减少多机器人系统搬运货物的时间，但是当机器人数目达到一定数量时，机器人系统完成任务所需时间的减少趋势变得缓慢。因为当机器人数目不断增加时，交通堵塞程度也在增加，无论选择通过牺牲路径代价来换取系统时间还是选择等待，都将造成资源浪费，所以需要根据智能仓库的大小来调节机器人的数目，达到合理利用资源的目的。

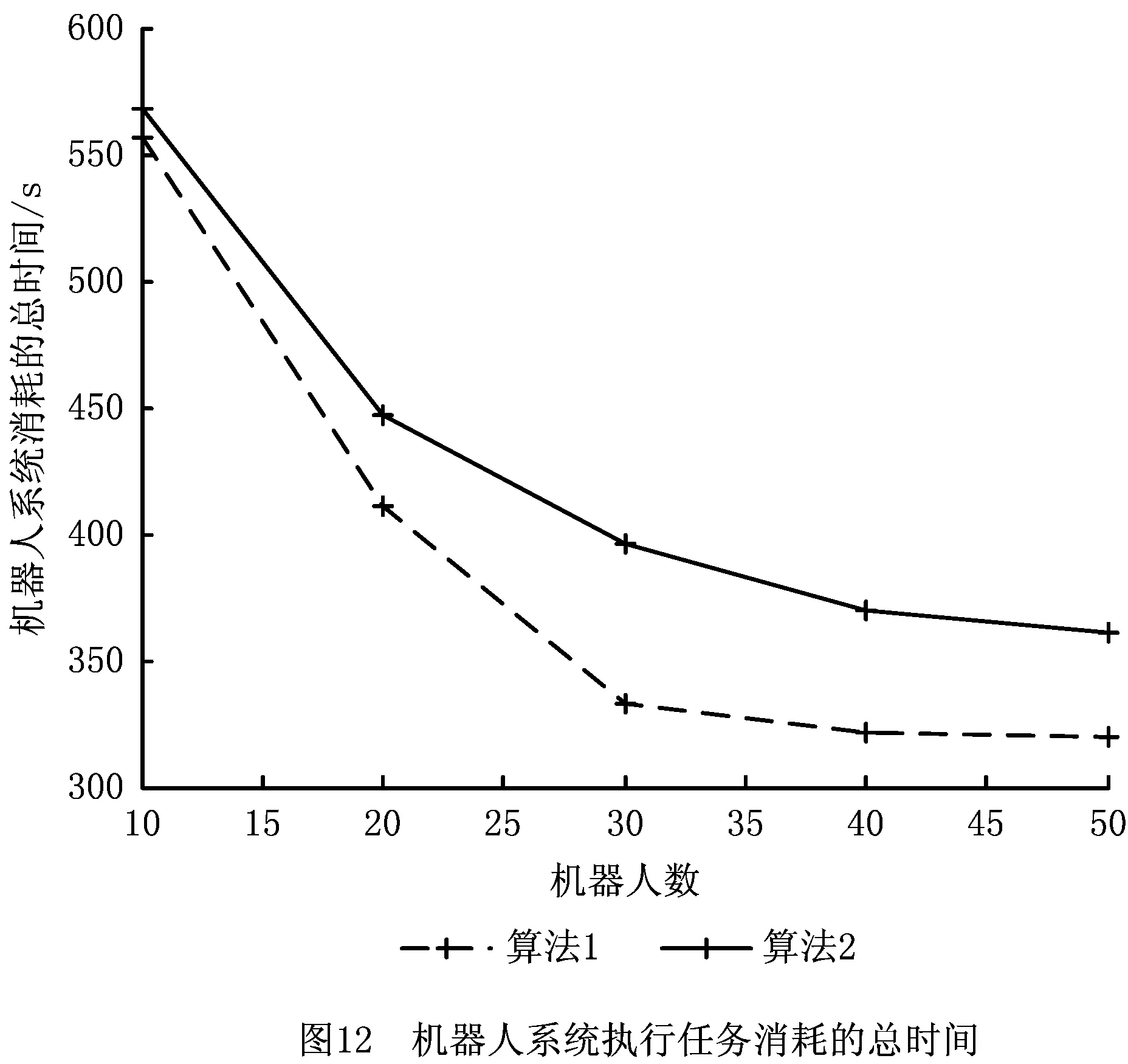
图13所示为使用不同数目机器人的多机器人系统在使用不同路径规划算法后，搬运300个货物所行走的总路程。机器人系统搬运货物行走的总路程随着工作机器人数目的变化而变化。多机器人系统使用算法1后，通常会比算法2行走更多的路程。这是因为随着机器人数目的增多，交通堵塞的情况也随之增多，机器人为了避开交通堵塞节约系统时间，选择通过牺牲一部分路径代价来满足时间要求。

图14所示为固定机器人数目为30的机器人系统使用不同路径规划算法后，执行不同数目的任务订单所花费的总时间。随着货物的增多，机器人系统完成任务的时间随之增多。相对于算法2，使用算法1能有效减少多机器人系统搬运货物的时间，而且随着货物的增多，机器人运行时间的增长，机器人间发生拥塞的概率也在增加，算法1则能有效避免碰撞，为系统节约更多的时间。另外，算法1所花费的时间随着机器人数目的增多或者货物的增多而呈线性增长，说明算法的复杂程度稳定，有很好的扩展性。

5 结束语

本文为智能仓库中多机器人路径规划提出一种动态加权地图与预约表下改进的A*算法。并且通过仿真实验，验证了该方法的可行性和高效性。本文未对订单任务分配进行详细研究。未来将研究智能仓库中货物订单的分配，并将订单分配与多机器人系统的路径规划结合起来，进一步完善智能仓库并提高智能仓库的效率。

[1] RUAN Xiaodong. The coming of the era of intelligent logistics robot[J]. New Economy Weekly,2016(11)：68-72(in Chinese)[阮晓东.智能仓储物流机器人时代的来临[J].新经济导刊,2016(11):68-72.]

[2] ZHANG Yi, FENG Yiping, RONG Gang. Reference model and key technologies of smart factory[J]. Computer Integrated Manufacturing Systems,2016,22(1)：1-12(in Chinese)[张 益,冯毅萍,荣 冈.智慧工厂的参考模型与关键技术[J].计算机集成制造系统,2016,22(1):1-12.]

[3] ZHANG jie, GAO Liang, QIN Wei, et al. Big-data-driven operational analysis and decision-making methodology in intelligent workshop[J]. Computer Integrated Manufacturing Systems,2016,22(5)：1220-1228(in Chinese).[张 洁,高 亮,秦 威,等.大数据驱动的智能车间运行分析与决策方法体系[J].计算机集成制造系统,2016,22(5):1220-1228.]

[4] WILLIAMS K. A fulfilling position:villeneuve revolutionizing e-commerce[amperes:current affairs from around the world][J]. Women in Engineering Magazine IEEE,1942,8(2):12-16.

[5] D’ANDREA R. Guest editorial:a revolution in the warehouse:a retrospective on Kiva systems and the grand challenges ahead[J]. IEEE Transactions on Automation Science & Engineering,2012,9(4):638-639.

[6] HIKVISION. The Application in intelligent storage of HIKV-ISION “building” robot[J]. Intelligent Robot,2016(2)：81-84(in Chinese).[海康威视.海康威视“阡陌”机器人在智能仓储中的应用[J].智能机器人,2016(2):81-84.]

[7] MA Huijiao, WU Xiao, GONG Yulei, et al. A task-grouped approach for the multi-robot task allocation of warehouse system[C]//Proceedings of International Conference on Computer Science and Mechanical Automation. Washington, D.C.,USA:IEEE,2016:277-280.

[8] OLMI R L. Coordination of industrial AGVs[J]. International Journal of Vehicle Autonomous Systems,2011,9(1/2):5-25.

[9] SIMEON T, LEROY S, LAUUMOND J P. Path coordination for multiple mobile robots:a resolution[J]. Robotics & Automation IEEE Transactions on,2002,18(1):42-49.

[10] HABIB D, JAMAL H, KHAN S A. Employing multiple unmanned aerial vehicles for co-operative path planning[J]. International Journal of Advanced Robotic Systems,2013,10(3):119-134.

[11] DIGANI V, SABATTINI L, SECCHI C, et al. Towards decentralized coordination of multi robot systems in industrial environments:a hierarchical traffic control strategy[C]//IEEE International Conference on Intelligent Computer Communication and Processing. Washington, D.C.,USA:IEEE,2013:209-215.

[12] RYU K, DANTANARAYANA L, FURUKAWA T, et al. Grid-based scan-to-map matching for accurate 2D map building[J]. Advanced Robotics,2016,30(7):431-448.

[13] MILLAN J D R, ARLEO A. Neural network learning of variable grid-based maps for the autonomous navigation of robots[C]//Proceedings of IEEE International Symposium on Computational Intelligence in Robotics and Automation. Washington, D.C.,USA:IEEE Computer Society,1997:40-45.

[14] GANESHMURTHY M S, SURESH G R. Path planning algorithm for autonomous mobile robot in dynamic environment[C]//Proceedings of the 3rd International Conference on Signal Processing, Communication and Networking. Washington, D.C.,USA:IEEE,2015:1-6.

[15] LEACH A R, PROUT K. Automated conformational analysis:directed conformational search using the A*algorithm[J]. Journal of Computational Chemistry,1990,11(10):1193-1205.

[16] STENTZ A. The focussed D*algorithm for real-time replanning[C]//Proceedings of the 14th International Joint Conference on Artificial Intelligence. New York, N.Y.,USA:ACM,1995,124(4):1652-1659.

[17] YUE Weiya, FRANCO J, YUE Hongwei, et al. Id*lite:improved D*lite algorithm[C]//Proceedings of the 2011 ACM Symposium on Applied Computing. New York, N.Y.,USA:ACM,2011:1364-1369.

[18] KARABOGA D, AKAY B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics & Computation,2009,214(1):108-132.

[19] BRAND M, MASUDA M, WEHNER N, et al. Ant colony optimization algorithm for robot path planning[C]//Proceedings of International Conference on Computer Design and Applications. Washington, D.C.,USA:IEEE,2010:V3-436-V3-440.

[20] PARKER L E. Path planning and motion coordination in multiple mobile robot teams[EB/OL].[2016-09-04].http://web.eecs.utk.edu/～leparker/publications/SpringerEncComplexSys_09.pdf.

[22] DIGANI V, SABATTINI L, SECCHI C. A probabilistic eulerian traffic model for the coordination of multiple AGVs in automatic warehouses[J]. IEEE Robotics and Automation Letters,2016,1(1):26-32.

[24] DORIGO M. Autonomous task allocation for swarm robotic systems using hierarchical strategy[C]//Proceedings of the 10th International Conference on Swarm Intelligence. Berlin, Germany:Springer-Verlag,2016,9882:287.

[25] LI Bin. Container terminal task scheduling oriented to PID control and simulation optimization[J]. Computer Integrated Manufacturing Systems,2016,22(3)：833-845(in Chinese).[李 斌.面向PID控制和仿真优化的集装箱码头作业调度[J].计算机集成制造系统,2016,22(3):833-845.]

[26] WU Tengyu, YU Haiyan. Online traveling salesman problem with linear penalty[J]. Computer Integrated Manufacturing Systems,2017,23(4)：913-920(in Chinese).[吴腾宇,余海燕.带有线性惩罚的在线旅行商问题[J].计算机集成制造系统,2017,23(4):913-920.]