基于双重最大实体要求的同轴度误差评定方法

黄美发,唐哲敏,孙永厚,彭治国,鲍家定

(桂林电子科技大学 机电工程学院,广西 桂林 541004)

0 前言

零件的尺寸和几何误差的评定包括对真实零件的评定[1]和对虚拟零件的评定[2]。前者在产品检测环节用于评定真实零件的几何特性和合格率，常采用测点模型来表示真实零件[3]；后者在产品设计环节用于评定虚拟零件[4-5]，预计零件或装配体的几何特性和合格率[6]。

尺寸误差和几何误差之间的补偿关系称为公差原则，包括独立原则(Regardless of Feature Size, RFS)、包容原则、最大实体要求(Maximum Material Requirement, MMR)、最小实体要求(Least Material Requirement, LMR)和可逆要求(Reciprocity Requirement, RPR)[7],其中MMR是体现零件可装配性的一种公差原则[8]。快速、准确地计算和评定零件的尺寸和几何误差，具有重要的意义。

当定向误差或定位误差(统称方位误差)应用有MMR时，可以通过通规或止规来检测产品几何特性的合格性[7]。Requicha等[9](1983)首先提出虚拟量规的概念，并建立了被测要素有MMR的二维数学模型，利用提出的模型可以产生虚拟零件并对虚拟零件进行评定，但这种模型没有考虑零件的形状误差[9]；蔡敏等[10](1999)将虚拟量规拓展到三维，建立了方位误差有MMR和RPR的三维零件数学模型，但仍然没有考虑零件的形状误差;Pairel[11](2007)进一步分析了方位误差有MMR的几种具体虚拟量规形式，并考虑了零件的形状误差。

真实零件的方位误差的基准不可避免地存在几何误差。为了提高前述模型的精度，Pairel[11](2007)研究了基准的优先等级，并分析了基准和基准体系的数学构建方法;李春丽[12](2013)进一步分析了基准优先顺序对误差累积极限的影响;Minguez等[13](2014)将虚拟量规方法应用到日益发展的非接触式测量方法中。

根据GB/T 16671-2009[14]，ISO 2692-2014[7]和ASME Y14.5-2009[15]的规定，可以在方位误差及其基准上同时应用MMR(M-M方位误差)，通过相关联的若干个量规检验零件的方位误差合格性。这样的误差规范能够在保证可装配性的前提下进一步扩大可接受的零件几何误差，从而降低生产成本，但并未给出M-M方位公差评定的数学方法，仍处于研究阶段。

Giordano M等[16](2007)建立了轴对称几何要素的M-M方位误差的数学模型和评定方法，并将三维问题作为多个截面上的二维问题来处理；Jiang等[17](2014)用公差映射法(Tolerance Map, T-Map)求解了M-M方位误差条件下被测圆柱要素的方位变动极限(3个空间平移变动和3个空间旋转变动)，将其M-M方位误差的数学模型扩展到三维，然而这种方法忽略了形状误差，难以应用于孔轴类零件以外的特征，而且不能直接用于误差评定；吴玉光等[18](2014)研究了孔的一种特殊的M-M位置度误差(第一基准要素是平面，第二基准要素是应用MMR的孔)，并将其转换成曲柄导杆机构和摆杆机构的组合，分析了被测要素M-M位置度的方位变动极限和各方位变动之间的动态约束，建立了该种误差的数学模型和评定方法，但是这种转换为特殊机构的方法也不易推广到其他的M-M方位误差分析中。因此，M-M方位误差的数学建模和评定方法仍然是计算机辅助公差设计及评定领域的热点和难点。

孔轴类零件广泛应用于机械工业，其M-M同轴度误差的被测要素和基准要素均为圆柱体，对应的综合量规是两个同轴圆柱，因此M-M同轴度误差是具有代表性的、相对简单的M-M方位误差形式，可以作为M-M方位误差三维建模和评定方法研究的切入口。同时，三维坐标变换是一种通用性较强的零件运动仿真方法，可以用于模拟被测零件在量规中的调整运动。

本文研究M-M同轴度误差的虚拟量规的建立方法，根据M-M同轴度误差的工程语义，分析真实量规的几何特性及其在合格性评定中的使用过程，用坐标转换法建立相应的虚拟量规和合格性评定数学模型，为产品的检测与设计提供合格性检验的数学工具，为建立其他M-M方位误差的数学模型提供参考。

1 M-M同轴度的几何约束

1.1 M-M同轴度的几何约束

M-M同轴度误差对被测圆柱体和基准圆柱体有如下要求[7,14-15]：

(1)被测圆柱体和基准圆柱体的局部尺寸分别介于其各自的最大实体尺寸(Maximum Material Size, MMS)和最小实体尺寸(Least Material Size, LMS)之间。

(2)被测圆柱体和基准圆柱体均不得违反其各自的最大实体实效边界(Maximum Material Virtual Boundary, MMVB)。

(3)被测圆柱体的MMVB与基准圆柱体的MMVB同轴。

(4)被测圆柱体的MMVS等于MMS加上(轴)或减去(孔)其同轴度公差值。

(5)当基准圆柱体的轴线没有标注几何公差要求，或者注有几何公差但没有MMR时，基准圆柱体的MMVS为其MMS；当基准圆柱体的轴线注有形状公差，且有MMR时，基准圆柱体的MMVS由MMS加上(轴)或减去(孔)该形状公差值。

1.2 M-M同轴度的物理检验方法

当要求(1)满足时，可以用真实的综合量规检验M-M同轴度[7，14-15]。例如：图1a所示零件的M-M同轴度可以通过图1b所示的综合量规进行检验，方法如下：综合量规由A，b两段量规孔构成，且两段量规孔同轴；b段量规孔的直径为被测要素b轴的最大实体实效尺寸(MMVS)；A段量规孔的直径为基准要素A轴的MMVS；综合量规必须通过被测真实零件。

该方法涵盖了要求(2)～(5)，但存在以下问题：①量规成本较高，不适用于中小批量生产；②量规和产品规格一一对应，测量柔性小；③不能在设计阶段对虚拟零件进行检测。为了提高检测方法的柔性并实现对虚拟零件的检测，下面将建立与上述方法相对应的虚拟量规及合格性评定数学模型。

2 M-M同轴度的数学评定方法

在机械零件的造型阶段，会给出零件的名义几何形状和尺寸，但是实际加工出来的真实零件不可能完全达到名义几何形状和尺寸。目前，可以通过CAD建模、加工仿真[19]、构建肤面模型[20]等方法得到接近实际情况的虚拟零件，并用若干连续函数或离散点集来表示。本文评定的对象可以是真实零件或虚拟零件，为方便起见，将真实零件和虚拟零件统称为实际零件。

在对实际零件进行误差评定前，首先要获取其测点数据。对于真实零件，要获取其基准圆柱体和被测圆柱体的测点数据；对于用连续函数表示的虚拟零件，要计算出若干个基准圆柱体和被测圆柱体上的点，用来构成相应的测点数据；对于用离散点表示的虚拟零件，要提取其中若干个离散点，用来表示相应的测点数据。测点的分布及可靠性在相关文献里有大量讨论[21]，本文不再赘述。

所获取的测点数据构成了虚拟几何要素，并分别用来表示被测真实零件或虚拟零件的基准几何要素和被测几何要素。用虚拟量规对被测实际零件或虚拟零件进行数学评定，实际上是对其虚拟几何要素进行评定。

虚拟量规是一种理想的几何概念，不存在实体，可以用数学的方式体现，也可以用可视化的方法来展现。与综合量规的理想几何特性[7，15]相同，M-M同轴度误差的虚拟量规由被测圆柱体的最大实体实效边界MMVBb和基准圆柱体的最大实体实效边界MMVBA构成，并满足要求(3)～(5)，如图2所示。

用虚拟量规对虚拟几何要素进行数学评定的原理为：先将虚拟量规固定在局部坐标系中，再将实际被测圆柱体侧面和实际基准圆柱体侧面的几何要素在局部坐标系中进行调整(平移和转动)；如果实际被测圆柱体侧面和实际基准圆柱体侧面的几何要素能够同时被相应的MMVB包容(轴)或包容相应的MMVB(孔)，则被测零件符合给定的M-M同轴度公差，否则零件不合格，如图2所示。

2.1 虚拟量规的数学模型

由要求(3)可知MMVBb和MMVBA是两个同轴的无限长度的圆柱，其轴线的方位决定了MMVBb和MMVBA的方位。

为便于理解和计算，可以将该轴线置于局部坐标系的一个坐标轴上(本文置于z轴上)，即该轴的方向向量nVA在局部坐标系中的坐标nVA,L为(0,0,1)，该轴上一个点pVA在局部坐标系中的坐标pVA,L为(0,0,0)，如图4所示。

由要求(4)可知，轴和孔的MMVBb的直径Dvb分别为

(1)

式中：Dbm为被测圆柱的最小实体尺寸；DbM为被测圆柱的最大实体尺寸；Tcoa为被测圆柱上标注的同轴度公差值。

由要求(5)可知，MMVBA的直径DvA为

(2)

式中：DAm为基准圆柱的最小实体尺寸；DAM为基准圆柱的最大实体尺寸；TA为基准圆柱上标注的几何公差值。

2.2 实际零件的误差评定

基于2.1节所述的虚拟量规，参考1.2节所述的M-M同轴度误差的物理评定方法，按照以下步骤对真实零件或虚拟零件的测点数据进行M-M同轴度误差评定，如图3所示。

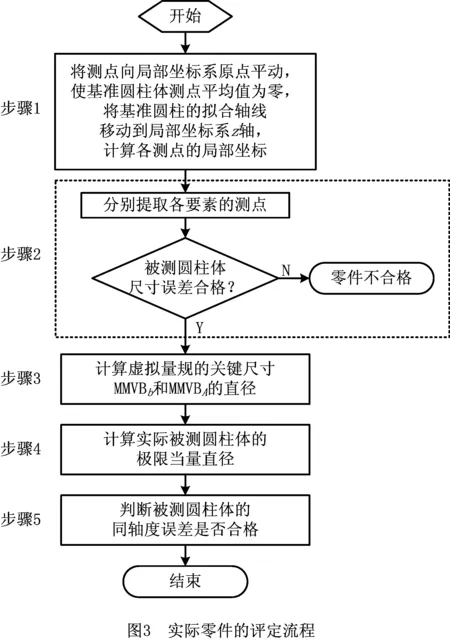
2.2.1 将实际被测零件置于局部坐标系中

如2.1节所述，将实际被测零件的测量坐标置于虚拟量规中。为了提高数值计算的精度，先将基准圆柱体和被测圆柱体的测点向局部坐标系原点移动(包括平移和旋转)，使基准圆柱体的测点的算数平均值为零，如式(3)和图4a所示。因为只是粗略移动，所以测点的此次移动只需平移。

具体的数学方法如下：

首先，向局部坐标系原点移动(平动)实际被测零件的测点，如式(3)和图4a所示。

(3)

式中：pb,m=(xb,m,meas,yb,m,meas,zb,m,meas)T和pb,m,T=(xb,m,T,yb,m,T,zb,m,T)T分别为被测圆柱体上编号为m的点的三维坐标测量值和第一次移动后在局部坐标系中的坐标值，m=1,…,M；pA,n=(xA,n,meas,yA,n,meas,zA,n,meas)T和pA,n,T=(xA,n,T,yA,n,T,zA,n,T)T分别为基准圆柱体上编号为n的点的三维坐标测量值和第一次移动后在局部坐标系中的坐标值,n=1,…,N。

然后，将实际基准圆柱的拟合轴线较精确地移动到局部坐标系z轴(包括平动和旋转)，并计算各测点的局部坐标，如图4a和图4b所示。因为最终的评定精度由2.2.4节步骤决定，所以本节中“实际基准圆柱的拟合轴线”的拟合规则并不十分严格，可以是最小外切原则、最大内接原则、最小区域原则、最小二乘原则等常见的拟合规则。本文采用最小外切圆柱拟合实际基准轴，即当实际基准圆柱的拟合圆柱的轴线移动到局部坐标系z轴时，实际基准圆柱的测点到局部坐标系z轴的最大距离最小。所述的拟合及移动可以用目标优化问题表述如下：

mindA,n,S,dA,n,S=2max|pA,n,S·nVA,L|。

s.t.

pA,n,S=(x2,y2,0)+

(4)

其中：dA,n,S是以局部坐标系原点为圆心的小外切圆的直径；目标优化问题的最优值dA,n,S,m=mindA,n,S,是实际基准圆柱的最小外切圆柱的直径；(x2,y2,0)为实际基准圆柱第二次移动时的平移向量；α2，β2分别为实际基准圆柱第二次移动时绕局部坐标系x轴和y轴的旋转弧度；x2m，y2m，α2m，β2m为最优解；

为旋转矩阵[6]，体现了每个测点先绕局部坐标系x轴旋转α2弧度，再绕局部坐标系y轴旋转β2弧度而引起的坐标变动。

该目标优化函数在最优解附近没有明显的下降方向，因此可以采用集群智能算法(如粒子群算法[22])进行求解。下文的目标优化问题具有和本目标优化问题相同的特点，也可以用相同的方法进行求解。

完成该步操作后，实际被测零件的测点移动到了下列位置(如图4b)：

(5)

式中：pb,m=(xb,m,yb,m,zb,m)T为被测圆柱体上编号为m的点第二次移动后在局部坐标系中的坐标值；pA,n=(xA,n,yA,n,zA,n)T为基准圆柱体上编号为n的点第二次移动后在局部坐标系中的坐标值；R(α2m,β2m)体现了每个测点先绕局部坐标系x轴旋转α2m弧度，再绕局部坐标系y轴旋转β2m弧度而引起的坐标变动。

2.2.2 检测实际零件是否满足要求(1)

根据要求(1)，实际被测圆柱和实际基准圆柱的局部尺寸要各自介于其MMS和LMS之间，即

(6)

式中：db,j为被测圆柱体上编号为j的局部直径，j=1，2，…，J；dA,l为基准圆柱体上编号为l的局部直径，l=1，2，…，L。

2.2.3 计算虚拟量规的关键尺寸

满足要求(3)～(5)的虚拟量规的关键尺寸包括MMVBb的直径Dvb和MMVBA的直径DvA，其计算方法分别如式(1)和式(2)所示。

2.2.4 计算实际被测圆柱的极限当量直径

实际被测圆柱体的体作用尺寸指轴(孔)的最小外切(最大内接)圆柱的直径。

实际被测圆柱体的当量直径指与MMVBA同轴的、实际被测圆柱的外切(轴)或内接(孔)圆柱的直径，如图4c～图4d所示。

实际被测圆柱体的极限当量直径指当MMVBA包容(轴)或包容于(孔)实际基准圆柱体时，通过移动被测零件得到的最大(轴)或最小(孔)当量直径，如图4c和图4d所示。

以图4c和图4d所示的阶梯轴为例，完成2.2.1节步骤后，实际基准轴(孔)的最小外切(最大内接)拟合基准轴线与局部坐标系z轴重合，实际零件处于如图4b所示的位置和方向。然后，实际被测轴(孔)移动并靠近(远离)局部坐标系z轴，以得到更小(大)的当量直径。在实际被测轴(孔)的移动过程中，牵连实际基准轴(孔)进行移动，如果移动过程中实际基准轴(孔)始终没有接触MMVBA，则实际被测轴(孔)的当量直径最小(大)可以达到其体作用尺寸；如果实际基准轴(孔)接触到了MMVBA，则实际被测轴(孔)的移动过程会受到限制，使被测轴(孔)的当量直径达不到其体作用尺寸，在这种情况下，实际零件会在如图4c(或图4d)所示的位置和方向取得其极限当量直径。

上述移动过程及目的用目标优化问题表述如下：

C0mindb,AM,coa,db,AM,coa=2maxC0|pm·nVA,L|。

s.t.

dx,dy∈[-τM,τM],dα,dβ∈[-τM/LA,τM/LA];

轴:C0=1;孔:C0=-1;

m=1,2,…,M,n=1,2,…,N。

(7)

式中：|db,AM,coa|为实际被测圆柱的当量直径；目标优化问题的最优值db,AM,coa,mM=C0mindb,AM,coa为实际被测圆柱的极限当量直径；(dx,dy,0)为实际基准圆柱第三次移动时的微小平移向量；dα,dβ分别为实际基准圆柱第三次移动时绕局部坐标系x轴和y轴的微小旋转弧度；sin dα≈dα，sin dβ≈dβ，cos dα≈1，cos dβ≈1；R(dα,dβ)为旋转矩阵[6]，体现每个测点先绕局部坐标系x轴旋转dα弧度，再绕局部坐标系y轴旋转dβ弧度而引起的坐标变动。

以实际基准圆柱体在MMVBA中的移动极限为参考，给出实际零件第三次移动时各变量(dx，dy，dα，dβ)的极限值，可以缩小寻优范围、提高运算效率、增加运算稳定性。

2.2.5 判断被测圆柱体是否合格

当实际被测圆柱体的极限当量直径db,AM,coa,mM不大于(轴)或不小于(孔)MMVBb的直径Dvb时，实际零件能通过虚拟量规，满足要求(2)～(5)。如果步骤2中检验得到实际零件也满足要求(1)，则被测零件满足设计要求的M-M同轴度公差，即

(8)

3 实例验证

图5所示为某阀芯的尺寸与几何公差的初步规范(本章的尺寸单位为mm)，实际零件在三坐标测量机上的测量数据如表1所示，本章用所提方法对实际零件的M-M同轴度进行评定。三坐标测量机为Hexagon Metrology(Qing Dao)生产的GLOBAL CLASSIC SR 07.10.07，测量精度为0.003。

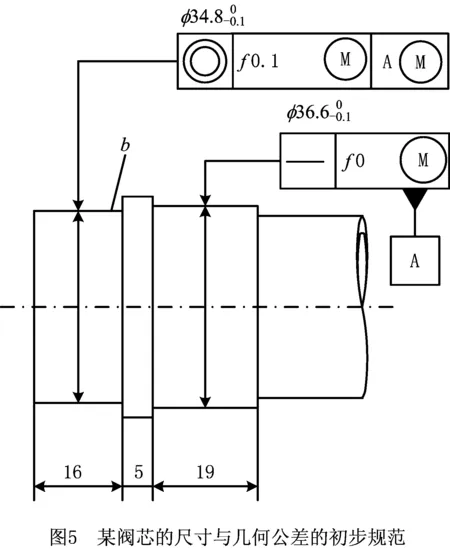
表1 实际零件的测量数据

pb，m，measpA，n，measmxb，m，measyb，m，measzb，m，measnxA，n，measyA，n，measzA，n，meas127848816046584069129212321511610363228084418341584066229945819986610122328502720895584065330322717680610128428865220505840654306261145436101355295469221665840685308136113976101416299412101658407363095536644610149730381118392584078730965223836101558309378108445840938307552-4304610163931060427995841059301738-1050561016810306716-720158411510297362-124986101711300141-1240758411811286525-1226661010512297276-1346058411912279399-747761009713291746-141315841181327497348461007814287784-13566584115142791891546461006115283607-1191858411115286996206496100551627799-717858410216300686-1113261343517274428765858884117303238-9429613434182757691176858883518305471-727961343219277491475858883119307049-5158613429202801711776558882820308039-336761342721284484206465888242130960619446134212228819321951588825223096935425613417

续表1

(1)将实际被测零件置于局部坐标系中

首先，向局部坐标系原点移动实际被测零件的测点，即将数据代入式(3)，得

(9)

然后，将第一次移动后的实际基准圆柱的最小外切圆柱的轴线移动到局部坐标系z轴，即将pA,n,T代入式(4)，用粒子群算法[22]求解目标优化问题，解得：目标优化问题的最优值dA,n,S,m=mindA,n,S=36.586为实际基准圆柱的最小外切圆柱的直径；最优解x2m，y2m，α2m，β2m分别为0.009 1，-0.005 6，0.000 4，0；(x2,y2,0)=(0.009 1,-0.005 6,0)为实际基准圆柱第二次移动时的平移向量；α2=0.000 4，β2=0分别为实际基准圆柱第二次移动时绕局部坐标系x轴和y轴的旋转弧度。

最后，将pb,m,T，pA,n,T和x2m，y2m，α2m，β2m代入式(5)，得到实际被测零件的测点第二次移动后的位置：

(10)

(2)检测实际零件是否满足要求1

(11)

经过两次移动后，实际被测圆柱体上的测点到z轴(拟合圆柱轴线)的最大距离的2倍(不小于最大局部尺寸)为34.787,最小距离的2倍(不大于最小局部尺寸)为34.720；实际基准圆柱体上的测点到z轴的最大距离的2倍为36.586、最小距离的2倍为36.523。实际零件满足要求(1)。

(3)计算虚拟量规的关键尺寸

将数据代入式(1)和式(2)，得：

(12)

(4)计算实际被测圆柱的极限当量直径

将DvA，pb,m，pA,n和LA代入式(7)，得：

mindb,AM,coa,db,AM,coa=2max|pm·nVA,L|。

s.t.

dx,dy∈[-τM,τM]=[-0.013 6,0.013 6];

dα,dβ∈[-τM/LA,τM/LA]=[-0.004,0.004];

m=1,2,…,48,n=1,2,…,48。

(13)

用粒子群算法求解上述目标优化问题[22]，解得实际被测圆柱的极限当量直径db,AM,coa,mM=mindb,AM,coa=34.787。

(5)判断被测圆柱体是否合格

db,AM,coa,mM=34.787<34.9=Dvb，满足式(8)，即满足要求(2)。

综上所述，实际被测零件同时满足要求(1)～要求(5)，符合其设计的M-M同轴度公差要求。

3.1 基于T-Map法的评定

如前所述，现有的误差评定方法难以评定产品的M-M方位误差。其中，T-Map分析了实际被测圆柱要素相对于实际基准圆柱要素的方位变动，建立了M-M方位误差的三维数学模型，并且能应用于M-M同轴度误差建模上[17]。相对于其他现有研究，虽然T-Map法忽略了零件形状误差，但较容易应用于M-M同轴度误差的评定。因此，本文用基于T-Map法的误差评定方法作为所提评定方法的对照，分析所提方法的优缺点。

T-Map法将被测要素和基准要素都视为没有形状误差的直圆柱[17]。因此，要将T-Map法应用于真实零件的M-M同轴度误差评定，必须先分别用实际被测要素和基准要素的拟合圆柱体来替代实际被测要素和基准要素。因为M-M同轴度误差控制的是被测零件的边界，所以本文使用最小外接圆柱体来拟合实际圆柱体。

T-Map法建立的数学模型是从设计和模拟的角度出发，给出了拟合要素之间的约束关系和虚拟零件的产生方法。然而，因为该数学模型没有考虑评定时的要求，所以T-Map法没有给出判断“某个现有的虚拟零件或真实零件的拟合要素是否合格”的方法。本文将T-Map法中的多参数约束问题转化为有约束目标优化问题，从而解决判断“某个现有的虚拟零件或真实零件的拟合要素是否合格”的问题。

综上所述，本文首先将T-Map法拓展到如图5所示的M-M同轴度误差建模；然后分别用实际基准圆柱体和实际被测圆柱体的最小外接圆柱体替代表1所示的真实零件的实际基准圆柱体和实际被测圆柱体；最后用有约束目标优化问题来判断零件的合格性。具体计算过程如下：

(1)将T-Map法应用于M-M同轴度误差建模，可以得到实际基准圆柱体和实际被测圆柱体的最小外接圆柱体间的数学约束模型如下：

Dvb-db;

(14)

DvA-dA。

(15)

(16)

式中：LA=19和Lb=16分别为基准圆柱体和被测圆柱体的名义长度，LAb=22.5为其各自几何中心之间的名义距离；dA和db分别为实际拟合基准圆柱体和实际拟合被测圆柱体的直径；(dxAb,dyAb,0)和(drxAb,dryAb,0)分别为实际拟合被测圆柱体相对于实际拟合基准圆柱体的平移变动和旋转变动，是通过拟合圆柱体计算得到的；(dxA,dyA,0)和(drxA,dryA,0)分别为实际拟合被测圆柱体相对于MMVBb的平移变动和旋转变动，是受约束的变量；(dxb,dyb,0)和(drxb,dryb,0)分别为实际拟合基准圆柱体相对于MMVBA的平移变动和旋转变动，是中间变量，由前述其他变量计算得到。

(2)将表1中的数据进行最小外切圆柱拟合后，得到：dA=36.586，db=34.787，(dxAb,dyAb,0)=(-0.0179,-0.0246,0)，(drxAb,dryAb,0)=(0.0015,0.0007,0)。

(3)用有约束目标优化问题判断零件的合格性。如前所述，T-Map法只构建了M-M方位误差的数学模型，并没有给出判断一个实际零件的实际参数是否满足式(14)的方法。本文将式(14)左边的最小值作为优化目标，式(15)和式(16)作为约束，通过计算并判断式(14)左边的最小值是否满足式(14)，来判断表1所示的真实零件是否满足T-Map法给出的约束。

将dA,db,dxAb,dyAb,drxAb,dryAb代入式(14)～式(16)得：当(dxA,dyA,0)=(0.001 2,0.002 8,0)，(dxA,dyA,0)=(-0.000 7,-0.000 4,0)时，式(14)左边取最小值0.066，小于式(14)右边的0.013。

因此，T-Map法评定的结果是：表1所示的真实零件满足数学模型给出的约束(式(14)～式(16))，符合图5所示的M-M同轴度公差的要求。

3.2 对比分析

本文所提评定方法和基于T-Map法的评定方法对表1所示的真实零件的评定结果都是“符合图5所示的M-M同轴度公差要求”。

应用T-Map法进行评定，当式(14)左边取最小值时，被测拟合圆柱体能取得最小当量直径为0.066+db=0.066+34.787=34.853,比用所提评定方法得到的数值34.787大0.066，这个差值远大于测量设备的精度0.003，是可信的。

因为两种方法的实际基准圆柱体均未超出其MMVBA，所以所提评定方法比基于T-Map法的评定方法精确。两种评定方法所得结果之间的差值(0.066)与图5中标注的同轴度误差要求0.1为一个数量级，是显著的，这是因为：基于T-Map法的评定方法用最小外切圆柱体包容和替代了实际基准圆柱体，而被包容的有形状误差的实际基准圆柱体在其MMVBA中有更大的调整量，如图6所示。

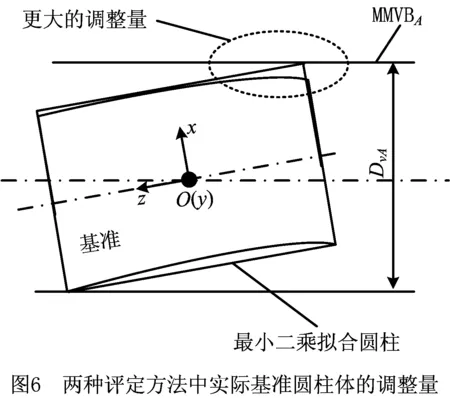
对比两种方法的数学评定过程，可以观察到：用提出的基于虚拟量规的评定方法来评定大型测点集时，其计算量比本文基于T-Map法拓展得到的评定方法的计算量大得多。

4 结束语

本文根据M-M同轴度误差的工程语义，分析了综合量规的几何特性及其在误差评定中的使用过程，提出了M-M同轴度误差的数学评定方法。该方法首先，建立了相应的虚拟量规数学模型；然后，基于虚拟量规，建立了实际的真实零件和虚拟零件的误差评定数学模型；最后，通过粒子群算法求解了该数学模型，并判断被测零件是否符合M-M同轴度公差要求。

文中以图5所示的某阀芯为例，评定给出的真实零件，并给出其“符合M-M同轴度误差要求”的结论。将传统的T-Map误差建模方法应用于同一零件的M-M同轴度误差评定，得到了相同的结论。然而，通过比较评定出的误差值可以发现，所提评定方法比基于T-Map法的评定方法更精确。

通过与基于T-Map法的评定方法比较，可以发现所提方法的运算量较大。因此，对测点进行适当的预处理，以减少本文提出的评定方法的运算时间，是未来可以进行研究的一个课题。同时，因为所提方法能充分表达实际被测要素的形状误差，并且涉及目标优化算法，所以其不确定度的产生和传递也是一个复杂的问题，很难直接用现有的不确定度分析方法分析其不确定度。因此，本文在实例验证中通过采用高精度的测量设备来保证结果的可靠性。在未来的工作中，将通过多参数实验和蒙特卡洛模拟来分析基于虚拟量规的M-M同轴度误差评定方法的不确定度。

[1] HE Gaiyun, ZHANG Mei, SONG Zhanjie. Error evaluation of free-form surface based on distance function of measured point to surface[J]. Computer-Aided Design,2015,65(C):11-17.

[2] WANG Daqiang. The research on inspection and analysis method of geometric feature applied maximum material requirements[D]. Hangzhou:Hangzhou Dianzi University,2015(in Chinese).[王大强.最大实体要求下几何要素检验理论的研究[D].杭州：杭州电子科技大学,2015.]

[3] ANWER N, BALLU A, MATHIEU L. The skin model, a comprehensive geometric model for engineering design[J]. CIRP Annals-Manufacturing Technology,2013,62(1):143-146.

[4] SCHLEICH B, ANWER N, MATHIEU L, et al. Contact and mobility simulation for mechanical assemblies based on skin model shapes[J]. Journal of Computing & Information Science in Engineering,2015,15(2):979-985.

[5] HOFFMANN C, SHAPIRO V, SRINIVASAN V. Geometric interoperability via queries[J]. Computer-Aided Design,2014,46(1):148-159.

[6] HUANG Meifa, TANG Zhemin, SUN Yonghou, et al. Assembly tolerance modeling based on auxiliary assembly joints[J]. Computer Integrated Manufacturing Systems,2015,21(8):2033-2042(in Chinese).[黄美发,唐哲敏,孙永厚,等.基于辅助定位接点的装配误差建模[J].计算机集成制造系统,2015,21(8):2033-2042.]

[7] ISO. ISO 2692:2014 Geometrical product specifications(GPS)—Geometrical tolerancing. Maximum material requirement(MMR),least material requirement(LMR)and reciprocity requirement(RPR)[S]. Genevese, Switzerland:ISO,2014.

[8] CHAVANNE R, ANSELMETTI B. Functional tolerancing:virtual material condition on complex junctions[J]. Computers in Industry,2011,63(3):210-221.

[9] REQUICHA A A G. Toward a theory of geometric tolerancing[J]. International Journal of Robotics Research,1983,2(4):45-60.

[10] CAI Min, WU Zhaotong, GUO Jianping, et al. Tolerance consistence evaluation tool for computer-aided tolerance design-soft gauge[J]. China Mechanical Engineering,1999，10(11):1260-1263(in Chinese).[蔡 敏，吴昭同，郭建平，等.计算机辅助误差设计一致性的评定工具—软件量规[J].中国机械工程，1999,10(11):1260-1263.]

[11] PAIREL E. Three-dimensional verification of geometric tolerances with the “fitting gauge” model[J]. Journal of Computing & Information Science in Engineering,2007,7(1):26-30.

[12] LI Chunli. Study of the three tridimensional functional toleracne analysis method of the complex product[D]. Beijing:Beijing University of Technology,2013(in Chinese).[李春丽.复杂产品的三维功能误差分析方法研究[D].北京：北京工业大学,2013.]

[13] MINGUEZ R, ARIAS A, ETXANIZ O, et al. Framework for verification of positional tolerances with a 3D non-contact measurement method[J]. International Journal for Interactive Design & Manufacturing,2016,10(2):85-93.

[14] Standardization Administration of the People’s Republic of China. GB/T 16671-2009 Geometrical product specifications(GPS)-geometrical tolerancing-maximum material requirement(MMR), least material requirement(LMR), and reciprocity requirement(RPR)[S]. Beijing: Standards Press of China,2009(in Chinese).[全国文献工作标准化技术委员会.GB/T 16671-2009 产品几何技术规范(GPS) 几何误差最大实体要求、最小实体要求和可逆要求[S].北京：中国标准出版社，2009.]

[15] ASME. Y14.5-2009 Dimensioning and tolerancing- engineering drawing and related documentation practices[S]. New York, N.Y.,USA:ASME,2009.

[16] GIORDANO M, SAMPER S, PETIT J P. Tolerance analysis and synthesis by means of deviation domains, axi-symmetric cases[M]//Models for Computer Aided Tolerancing in Design and Manufacturing. Berlin, Germany:Springer-Verlag,2007:85-94.

[17] JIANG K, DAVIDSON J K, LIU J, et al. Using tolerance maps to validate machining tolerances for transfer of cylindrical datum in manufacturing process[J]. International Journal of Advanced Manufacturing Technology,2014,73(1/2/3/4):465-478.

[18] WU Yuguang, WANG Daqiang. Inspection method of geometric feature when datum flowing maximum material requirements[J]. Computer Integrated Manufacturing Systems,2014,20(11):2683-2689(in Chinese).[吴玉光,王大强.基准遵循最大实体要求时的几何要素检验方法[J].计算机集成制造系统,2014,20(11):2683-2689.]

[19] LEI Man, LYU Jian, LIU Zhenghong, et al. Surface machining simulation based on UG and vericut[J]. Machinery Design & Manufacture,2014(11):47-49,53(in Chinese).[雷 蔓,吕 健,刘征宏,等.基于UG与Vericut的复杂曲面加工仿真[J].机械设计与制造,2014(11):47-49,53.]

[20] ANWER N, SCHLEICH B, MATHIEU L, et al. From solid modelling to skin model shapes:shifting paradigms in computer-aided tolerancing[J]. CIRP Annals-Manufacturing Technology,2014,63(1):137-140.

[21] ZHANG Mei. Research on sampling strategy and profile error evaluation algorithm for free-form surface[D]. Tianjin:Tianjin University,2013(in Chinese).[张 美.自由曲面测量采样策略及轮廓度误差评定算法研究[D].天津：天津大学,2013.]

[22] DONG Yinyue. Optimal assembly tolerance design based on Monte Carlo method and modified PSO algorithm[D]. Wuhan:Huazhong University of Science and Technology,2011(in Chinese).[董银月.基于蒙特卡洛方法和改进PSO算法的装配误差优化设计[D].武汉：华中科技大学,2011.]