水准测量及其代替方法的研究
2018-03-19任海峰杨利兵
任海峰,杨利兵
(1.北京鼎春德正测绘中心,北京100029;2.邢台市城乡房产测绘队,河北邢台054000)
几何水准测量是当今的高程测量之中最重要的方法之一。然而,一般情况下的几何水准测量的效率,是差强人意的。另外,在长路线上作业的时候,还要受到累积效应的垂直折射光影响。虽然科研人员已经发现了一些公式折射误差修正,但这些公式还存在着系统误差。由于几何水准测量程序较复杂,所以其转点较多,并且仪器、标尺等也是会存在误差。正是由于这些复杂的原因,如果在地势不平坦的地区,例如山区或者丘陵等地高程的传递要通过几何水准测量是特别不容易的,有时甚至是不可能完成的一项任务。由于测量仪器的更新换代不断发展,许多研究人员对三角高程测量不断深入的研究,使三角高程测量的准确度也不断精确,误差不断减小。另外,全球定位系统被大量应用于高程测量中。
1 水准测量精度
1.1 水准测量原理和方法
水准测量原理是根据水准仪提供的水准视线,在前后视水准尺上读数,从而测量两点之间的高差为再计算点的高程。
当无法直接从已知点一次架仪器测量到待定高程点时,需要在两点之间选择一条合适的测量线路,中间确定一些转点,再利用测量高差取和,从而确定待定点高程。
1.2 水准测量的精度要求
水准测量的相关限差要求,见表1。
每公里水准测量往返高差中数偶然中误差和全中误差的限值列于表1中。

表1一二等水准测量每公里往返高差中数偶然中误差和全中误差的限值
测段路线往返测高差不符值、附合路线和环线闭合差以及检测已测测段高差之差的限值,见表2。

表2一二等水准测量的四项限差
2 全站仪三角高程测量
2.1 全站仪三角高程测量的原理
如图1所示,在A点处放好仪器,仪器高度可以设为i1。照准点是B,觇标高度为i2。R则为大地水准面上的曲率半径。分别为过P点和A点的水准面。是PE在P点的切线,为光程曲线。由图1可以看出,A到B,它们两个之间的高差为:
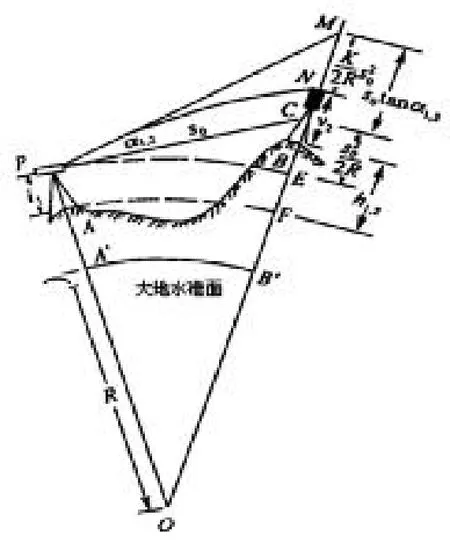
图1三角高程测量原理
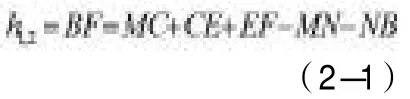
考虑地球曲率大气折光等的影响,上式可变为:C为球气差系数。

三角高程测量大部分情况下要进行对向观测,按图(3-1)有:
由测站A观测B点:

则测站B观测A点:
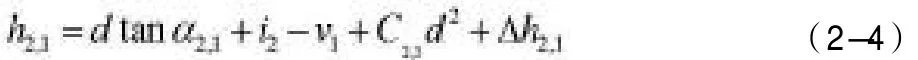
从以上两个式子,可得对向观测计算高差的基本公式:
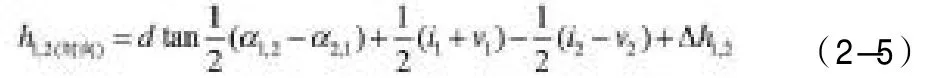
2.2 传统三角高程测量方法的改进——中间法三角高程测量
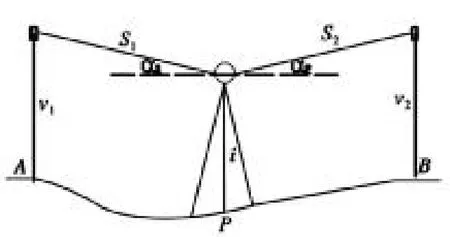
图2中间站三角高程测量示意图

在用三角高差进行施测的时候,每一站都应该单独测量两次,达到数据合格以后,将两次高差取平均。从而由一点高程计算出另一点高程。
2.3 中间站三角高程测量方法的优点
测站不存在对中这样的问题,仪器高是不需要被量取的,如果选择合适的方法,还可以不用测量棱镜的高。测站选在中间部分时,它能够非常有效的减少大气折射。效率高,需要的人手少。
3 三角高程测量的误差分析
从上面的三角高程测量的基本公式可以知道,其误差传播公式(3-1)为

由上面的公式可以知道,下面几个因素可以影响到三角高程测量的精度:
测距误差;仪器高与觇标高的测定误差;竖直角的测角误差。
4 三角高程测量代替二等水准测量方案设计
4.1 方案设计
本次实验选在华北某小区,实验主要目的是研究用三角高程测量代替二等水准是否可行。
水准测量仪器:Trimble DiNi03电子水准仪、铟瓦尺、尺垫、皮尺、数据线。
三角高程测量仪器:莱卡 TCR1201全站仪、棱镜、对中杆、电子气压计。
4.2 数据处理结果比较
本次实验所得数据处理结果,见表3。

表3三角高程测量高差与二等水准测高差的比较
这次测量共采集了九组数据,其中有三组数据,因为超过极限所以不适用。利用数据可求得=0.8mm,满足二等水准测量精度要求。
5 结论
本文研究用全站仪三角高程测量来取代二等几何水准测量,从而要确定精密三角高程测量的可行性。通过设计方案,做了一定量的数据采集,并分析其中的数据,它可以在一定条件下得出的结论,用全站仪三角高程测量代替二等水准测量一个可行的方案。与一般的几何水准测量方法相比,全站仪中间法三角高程测量,有更高的工作效率,而且精度满足要求。可以想象,将来很多情况下,可以用三角高程测量代替水准测量。
[1]孔祥元,郭际明.控制测量学(上册).第三版[M].武汉:武汉大学出版社,2006.
[2]武大测量学科组编.测量平差基础[M].武汉:武汉大学出版社,2009.
[3]潘晓风,杨正尧,程效军,等.数字测图原理与方法[M].武汉:武汉大学出版社,2004.
[4]徐伟,精密水准测量的误差来源及影响[J].科技信息,2009(07):383-383.
[5]李青岳,陈永奇.工程测量学[M].北京:测绘出版社,2008.
