爆扩桩抗拔极限承载力计算方法综述

康正炎

(1.安徽省·水利部淮委水利科学研究院，安徽 合肥 230088；2.安徽省建筑工程质量监督检测站，安徽 合肥 230000)

0 引言

随着重大工程建设项目的增多和海洋工程的建设发展，建筑物基础承受上拔力的情况也越来越多。在特定环境中，原来的承压桩可能承受拉拔荷载。例如上海500 kV世博变电站、海上石油钻井平台、珠海关后广场地下工程等。因此有必要对抗拔桩承载力问题进行研究。因传统等截面抗拔桩，其抗拔能力非常有限。为了提高桩的抗拔能力，非等截面形式桩主要是扩底桩，主要有人工挖孔桩、爆扩桩等。爆扩桩是扩底桩常用的方法之一。目的是用增加不多的材料和造价来显著提高桩基的极限抗拔承载能力。因此，在科技与经济上有很大的前景和效益，受到了工程界的青睐[1]。

本文在总结国内外学者对抗拔桩研究现状基础上，列举了常见计算爆扩桩极限承载力的方法，结合两组试桩试验，将试验结果与各种方法的计算值作比较，讨论各种方法的优缺点、适用性，为以后的工程中抗拔桩极限承载力设计提供一种思路和建议。

1 国内外研究现状的概述

下面简要介绍用不同方法研究抗拔桩的极限承载力的研究现状。

1.1 模型试验的研究

郭志昆(1988)采用弹塑性有限元法对桩的荷载传递进行了理论分析，找出了抗拔桩的承载机理，并且在南京和上海3个软土地基进行了爆扩桩的抗拔试验[2]。

刘文白(2003)通过现场原型试验研究了扩底抗拔桩在上拔荷载、水平荷载作用下的上拔位移和水平位移以及位移与荷载的关系。也研究了极限上拔承载力和抗拔桩的破坏机理。提出了极限上拔承载力的理论公式，理论计算结果与实测值是吻合的[3]。

王卫东(2007)设计了适用于上海地区的桩底形状与机具，并采用现场试验及等截面桩与扩底桩的抗拔承载力进行对比试验。结果表明，扩底抗拔桩的桩顶和桩端变形随荷载发展规律、桩身变形与回弹规律进行了初步探讨[4]。

孙洋波等(2010)根据上海某工程单桩、群桩的静载抗拔试验结果，分析了扩底和等截面桩在恒载作用下的抗拔稳定性[5]。

陈小强(2011)研究了单桩在抗拔与抗压条件下的承载力、桩身轴力及侧摩阻力分布规律的不同，在砂土中进行抗拔桩与抗压桩室内模型试验。结果表明，两者的桩身轴力分布具有相似的特性，摩阻力均从上部开始发挥并向下传递，随着荷载的增加，上部侧阻力变化减小，桩下身侧阻力迅速增长。抗拔桩桩身侧阻力表现为弱化效应，而抗压桩表现为强化效应[6]。

1.2 理论分析研究

许宏发(2000)基于有限元模拟，提出了扩大头段产生局部破裂，破裂面曲线采用了对数螺旋线表示，结合工程算例验证了爆扩桩的极限承载力。结果表明:计算结果与实测值比较吻合[7]。

王耀明(2007)在提出抗拔桩荷载位移曲线幂函数模型的基础上，得出了用幂函数曲率点估计抗拔桩承载力的方法，先将幂函数模型无量纲化，求得无量纲模型的曲率函数，再求导得到最大的曲率点，用该点函数作为极限承载力[8]。

郦建俊(2009)推导出了扩底抗拔桩中长桩土分层地基中极限承载力的简化公式，结合有关原位试验结果，对扩大头高度进行确定。同时还讨论了所提出方法在超长桩中的适用性。提出的简化分析方法能合理地揭示上海软土地区扩底抗拔桩中长桩的破坏机制，并获得了承载力一般规律[9]。

孙洋波(2011)结合上海地区部分工程实体试验和室内试验，对扩底桩与等截面桩的单桩抗拔承载力进行比较、分析了扩底桩抗拔承载力特性、提出了适用于软土地区扩底抗拔桩单桩承载力计算公式并对扩底桩的群桩效应进行了研究[10]。

1.3 数值模拟分析

刘文白(2004)对砂土上承受上拔荷载作用的基础进行数值模拟，并与模型试验结果进行对比。基于实验室模型试验和现场原型试验，测得土中滑裂破坏体为曲面锥台与圆柱的组合体，其破裂面与颗粒流数值模拟的结果符合良好，并分析了荷载-位移关系[11]。

吴江斌(2008)采用有限元分析程Marc模拟扩底抗拔桩扩大头作用机制[12]。

蒯行成(2010)建立扩底桩有限元模型，对扩底桩上拔荷载传递特性以及抗拔承载力进行了分析与研究[13]。

黄茂松(2011)提出了适用于不同桩长扩底桩的极限承载力的统一计算模式。假定扩大头处形成椭圆形局部破坏，而等截面段形成幂函数形式破裂面，幂函数曲线破裂面形状取决于土层或桩型参数。将计算结果与工程实测结果进行比较，验证了统一计算模式的正确性[14]。

2 扩底桩抗拔极限承载力计算

根据国内外学者通过模型试验、理论研究、数值模拟等不同的方法对抗拔桩承载力进行了研究的结果，本节总结了国内外抗拔桩典型计算公式。

2.1 国外规范中抗拔桩承载力公式

式中:m为工作条件系数，通常取1；u为桩表面周长；mf为桩侧土的工作条件系数；fi为仅与土种类有关i层允许摩阻力。

该公式只考虑等截面桩情形，未考虑带扩大头情况且不计桩自重，应用范围有限。

2.2 我国《建筑桩基技术规范》计算公式

现行的《建筑桩基技术规范(JGJ94-2008)的计算公式如下[15]:

式中:Puk抗拔极限承载力标准值；ui为桩身周长，等截面桩取ui=πd，对于扩底桩，按自桩底起算长度≤(4～10)d 时，取πD；反之，取πd；qsik为桩侧表面第i层土的抗压极限侧阻力标准值。λi为抗拔系数。土为砂土时取0.5～0.7；黏性土、粉土取0.7～0.8。

此公式是一个半理论半经验公式，虽考虑了桩底带扩大头的情况，但没有考虑扩大头上方土体作用而桩周阻力的变化情况，同样也没有考虑扩大头承载力和自重，但计算等截面桩还是比较合理的。

2.3 圆柱面剪切法

破坏面具体情况如图2所示。单桩抗拔承载力计算公式如下:

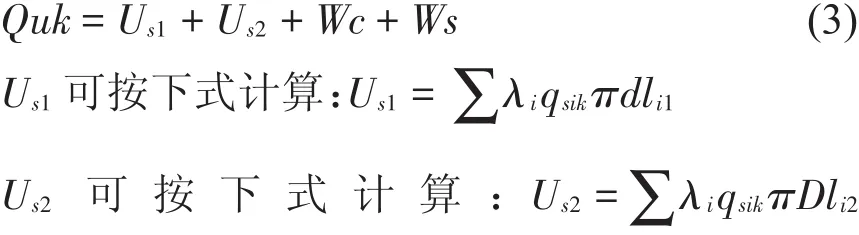
式中:li1为取大于H+H’长度；li2为取小于等于H+H’长度。

该法是一个经验公式，假设桩扩大头H及H’范围土体剪切面直径等于扩大头直径；同时超出此范围的侧摩阻力不受影响，分段参考我国现有规范的抗拔桩计算公式，比较容易计算抗拔桩极限承载力，但对于浅基础，计算结果偏差较大。

图2 圆柱面剪切法

2.4 Meyerhof-Adams法

基于在砂土中试验观察结果和测得数据，提出了计算模型如图3所示。Meyerhof&Adams假设:采用竖圆柱式滑动面替代模型试验中的观察到的喇叭形倒圆锥台形破裂面。两人将观察到的滑动面称为破坏面，由于破坏面承载力不便计算，所以乘以系数Ku即“竖直剪切面上土压力的标定上拔系数”。这样算的结果近似该破裂面的承载力，但实际已考虑了实际滑动面的等效因素。两位作者分别对浅基础和深基础极限承载力提出了计算公式[16-17]:

浅基础:

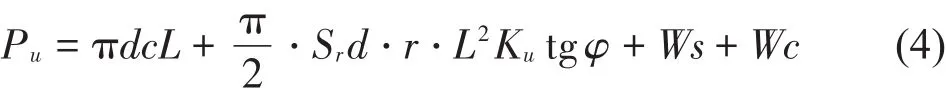
深基础:

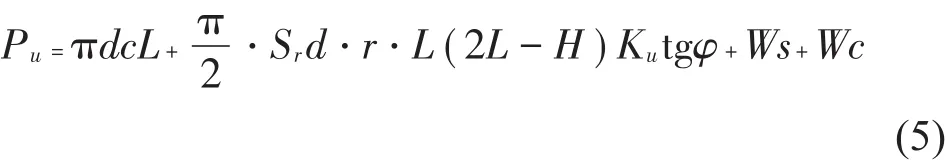
式中:Ws在高度H的圆柱体内包含的土体有效自重，d扩大头直径，c土的黏聚力，Sr为决定圆柱体侧表面上被动土压力大小的形状系数，φ为土的内摩擦角，Ku为竖直破坏面土压力上拔系数，取值见表1。

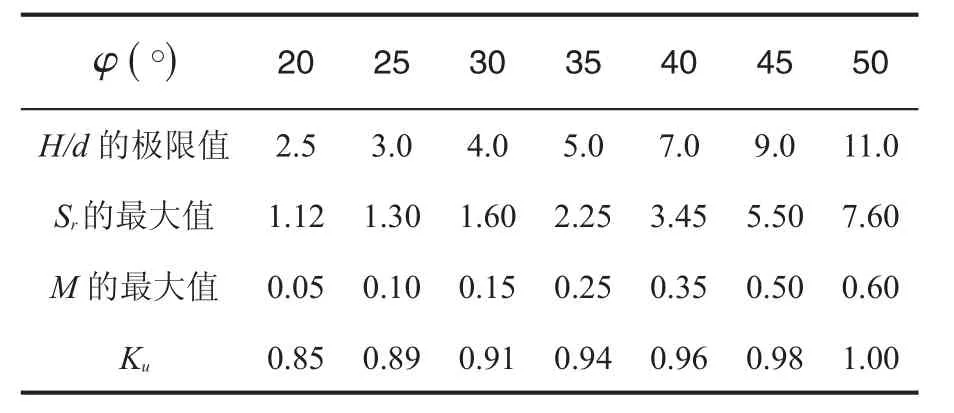
表1 不同内摩擦角时的H/d的极限值

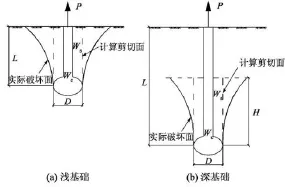
图3 Meyerhof-Adams计算模型

对于深基础，抗拔承载力随着深度而趋于某一极限值。因此存在着临界深度概念，在该临界深度以下桩扩大头的承载力不再能有效地提高[16]。

2.5 工程兵工程学院计算方法

工程兵工程学院与上海人防办科研所提出了适用于软粘土地质条件的爆扩桩抗拔力的计算公式为[18-19]:

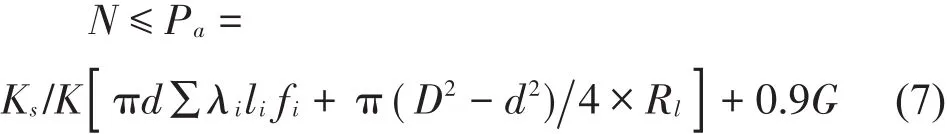
式中:N为轴向拉力；Pa为桩的容许抗拔力；Ks为施工因素等影响系数；K为安全系数，取2.0；Rl为扩大头上方土体极限承载力；G为桩有效自重；Ks的取值与很多因素有关，建议Ks的取值范围为0.8-1.3。

表2 桩侧摩阻力系数λi

2.6 文献[7]算法

许宏发依据有限元模拟，提出了扩大头段产生局部破坏，破裂面曲线可以采用对数螺旋线表示。

长扩大头的抗拔阻力由两部分组成，侧摩阻力和扩大头阻力。设n=D d，桩长径比m=l d，则对于粘性土，滑动面起始矢径rp0可由式(6)表示。

式中:d为桩的直径，φ为土的内摩擦角。这样，塑性区上边界深度zp可表示为:

图3 极限状态下，桩侧摩阻力示意图

则极限状态下，桩侧摩阻力为:

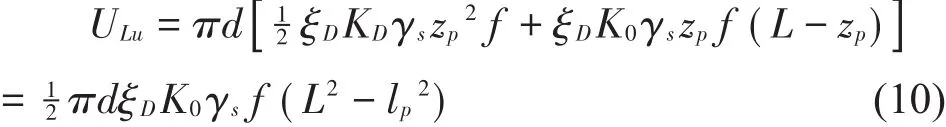
已知扩大头处土体的滑动面的形状为椭球面，其剖面线可以用对数螺旋线描述。简单给出扩大头抗拔阻力公式为:

因此，扩大头桩的总的极限抗拔力为:

式中:c 为土的黏聚力，Nc，Nq，Nr均为承载力系数，均可以查表得知，γs'为上层土体的加权平均重度。其他参数参见文献[7]。

此公式适用范围很广，各部分参数利用查表容易计算各部分极限承载力，适用于分层粘土和砂土计算，但没有对等截面段破坏面机理进行研究，而采用简化公式计算。

2.7 文献[1]算法

赵长青基于工程兵工程学院的研究，提出计算模型，如图5。抗拔极限承载力公式:

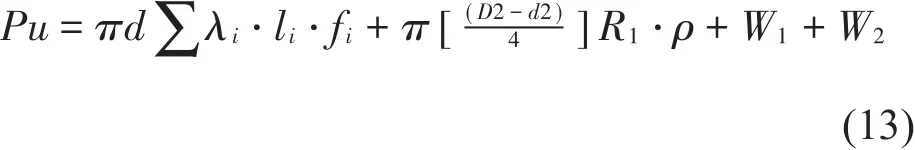
式中:λi桩侧摩阻力抗拔系数，见表2；ρ为扩大头形状系数取0.5，R1扩大头上方土体的抗压承载力；W1为桩自身重量；W2为桩头拖带土体的质量，可取桩身段土体质量。

3 试桩验证

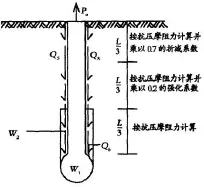
图4 计算模型

土层分布见图5所示，地下水位面在地表下2 m。试桩有两种[20]:扩大头深H=19.3 m上部自由段长h=9.8 m，L=18.7 m；扩大头入土深度H=22.7 m，上部自由段长h=13.2，L=22.1m，土的力学参数:试桩1取两土层的平均值，φ=7.3º，c=16 kPa；试桩2取φ=10º，c=23 kPa其他参数rs=8.5 kN/m3。ξD=0.88。两组试桩的抗拔极限承载力计算结果见表3。

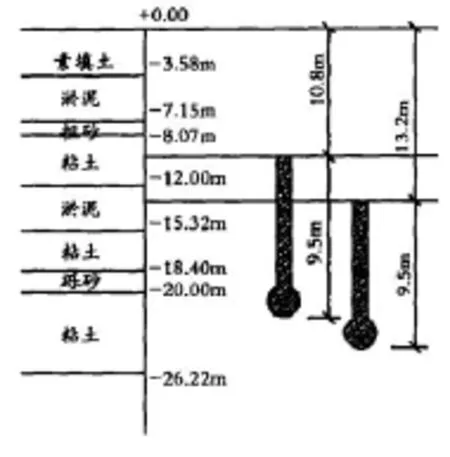
图5 桩桩试验示意图

试桩所处的土层有上层覆土，送桩部分上部均采用大管套小管的方法消除应挖除土层的摩阻力，因而计算过程中不考虑土层中桩体产生的桩周摩擦力，计桩长为9.5 m。从表3计算结果表明，文献[7]结果与试验值误差最小为-4.4%，-7.8%，文献[1]的误差为-11.4%，-2.4%，均可以作为估计爆扩桩极限承载力的方法。摩擦圆柱法没有不排水抗剪强度，无法计算。规范则误差较大，偏于保守。

4 结论

本文总结了计算爆扩桩极限承载力的不同计算方法，结合两组试桩试验，将试验结果与各种方法的计算值作比较，讨论各种方法的优缺点、适用性，得出了以下几点结论:

(1)从表3，可得规范计算的结果远远小于实际承载力值。首先此方法没有把桩自重考虑进去；规范中认为桩周的摩阻力沿桩长整个桩都小于抗压式的摩阻力，这与实际受力不符。故结果偏小很多。如果在设计抗拔桩时完全用这个公式估计抗拔桩极限承载力值，显然太过于保守，浪费材料且不经济。

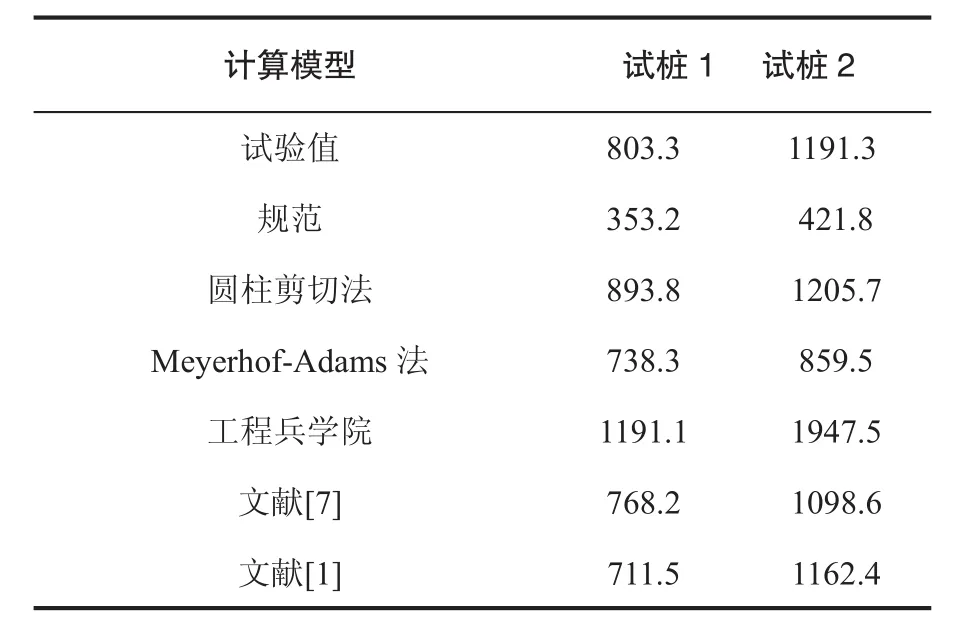
表3 不同模型计算结果与试桩结果的比较(kN)

(2)摩擦圆柱法是个经验公式，认为破坏面是个圆柱面，这样忽略了扩大头作用；圆柱面剪切法，是对前一种方法改进，更加贴近实际，计算结果更可靠。

(3)Meyerhof-Adams是一个半经验公式，此方法不仅可以计算浅基础也可计算深基础极限抗拔极限承载力，考虑了桩土之间的黏聚力、桩体自重和桩以上部分土体的自重。对于桩的扩大头作用采用乘以经验系数，相对于前面的方法有了很大的改进。

(4)工程兵学院的方法计算结果偏大于实际值。该公式不适用直径太大的爆扩桩，但公式比较完整，考虑了桩周阻力、扩大头作用和桩自重以及桩周阻力的分布不均匀性。

(5)文献[1]计算误差在15%以内，也较小，是对工程兵学院改进。文献[7]的方法比较理想的，误差比较小。公式(11)用理论法计算扩大头抗拔作用机理并且该计算公式里参数Nc，Nq，Nr均可以查表得出，适用于黏性土，适用范围最广。但此法还没有考虑等截面段土体的局部破坏作用。

为了更好地估算爆扩桩极限承载力，可参考文献[7]的计算公式，使其表格化，为更好应用到实际工程提供参考和意见。