基于可变模糊理论的气象干旱风险评价模型

颜 敏， 方国华， 闻 昕,2， 晋 恬

(1.河海大学 水利水电学院, 江苏 南京 210098； 2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室, 北京 100038)

1 研究背景

气象干旱是降水持续性短缺的自然现象[1]，水文干旱、农业干旱和社会经济干旱在一定程度上是气象干旱产生的结果。变化环境下，干旱事件的不确定性进一步加剧[2]，客观科学地评价气象干旱风险，对于把握干旱形成与发展机理、科学认识干旱事件的时空演变特征、防范和应对干旱灾害具有重要的科学意义和实际应用价值。

目前干旱风险分析常常选择主要的致旱因子，构建干旱风险综合评价指标体系。Okada等[3]认为自然灾害风险是由致灾因子危险性、承灾体暴露性和承灾体脆弱性3个因素共同影响。冯波等[4]采用标准化降水指数进行松花江流域的气象干旱评价，并通过风速、降水距平百分率、温度距平、气压、日照时数和相对湿度6个要素构造风险指数，进行气象干旱风险评估。王莺等[5]依据甘肃河东地区相关气象、生态和社会经济数据，在GIS平台下进行气象干旱灾害风险评估和区划。

气象干旱风险分析可以通过致旱因子构造风险指数进行表征，但存在风险因子选择以及权重确定的问题。为了规避上述问题，可以通过干旱发生概率以及相应的干旱损失量构造风险度，从而进行气象干旱风险的评估。Tobin等[6]提出风险度是由概率和易损度综合影响的结果。杜云等[7]以农业损失率作为农业干旱的损失量，并利用水文频率分析的方法，得到流域的农业干旱风险指数。孙鹏等[8]从危险度、易损度、风险度3个方面揭示了塔里木河流域干旱风险的空间变化特征。目前风险度在农业干旱风险分析中有所应用，但在气象干旱风险分析中应用较少。 并且，由风险度确定的干旱风险评价模型还存在着以下两个关键问题：第一、干旱识别作为干旱风险分析的基础存在阈值选择以及小干旱过程的问题。第二、风险度中的概率计算往往采用样本概率，而忽略了总体的概率分布特征。

为此，本文以“干旱识别-过程修正-风险分析”为主线，建立气象干旱风险评价模型，揭示流域气象干旱风险分布特征。首先，采用可变模糊理论方法进行干旱识别，规避了干旱识别过程中阈值选择问题；然后，考虑到前期降水影响，进行干旱过程的修正。同时利用游程理论对修正后的干旱过程进行频率分析，计算了总体的概率分布特征，增强了模型的适用性。接着，通过风险度表征干旱风险指数，避免了风险因子识别过程中因子权重确定以及因子选择问题，最后在淮河流域进行实例研究。

2 研究方法

2.1 基于可变模糊理论的气象干旱识别

干旱识别是干旱风险评价的基础，通常选用合适的指标对干旱进行辨识。但干旱与非干旱的界定是模糊的，存在阈值的选择问题。可变模糊评价方法[9-11]由于其物理意义明确，在评价模型中被广泛应用，本文在已有研究的基础上提出了基于可变模糊理论的干旱识别方法，通过历史资料构造干旱点和非干旱点，某一时刻的干旱评价可用该时刻对干旱点的综合相对隶属度表征，然后采用对立统一定理进行干旱识别。

2.1.1 可变模糊评价 干旱的可变模糊评价方法是通过对干旱点的综合相对隶属度表征干旱的水平，隶属度大则靠近干旱点，干旱水平高；隶属度小则远离干旱点，干旱水平低。由于干旱标准的时空差异性，不同的时间段，应构造不同的干旱点与非干旱点，形成干旱评价标准的可变集合。

根据月降水距平百分率和月连续无雨日数构造干旱点A和非干旱点Ac，见式(1)。

A=(minp,maxq)T, Ac=(maxp,minq)T

M=[A Ac]

(1)

式中：minp、maxq分别代表月降水距平百分率最小值和月连续无雨日数最大值; M为构造的模糊标准矩阵。

2.1.2 基于对立统一定理的干旱识别 对立统一定理[9]是寻找与连续区间边界点隶属度相等的一点，利用该点将连续区间划分成两个对立的集合，这一点可以看作划分对立集合的依据。

根据对立统一定理，必然存在某一点Q对于干旱点A和非干旱点Ac的相对隶属度相等，均为0.5，在Q点前后，对干旱的相对隶属度μA(t)和对非干旱的相对隶属度μAc(t)两者关系发生了变化，可以看作是干旱与非干旱的过渡阶段，而点Q可以作为划分干旱与非干旱的依据。

本文选取干旱的综合相对隶属度X0=0.5作为截断水平，用于判断干旱发生与否，在该截断水平以上认为发生干旱，反之则不发生，如图1所示，Xt在一个或多个时段内连续大于X0时，则出现正游程；反之出现负游程。由于纵坐标X是对干旱的综合相对隶属度，正游程是指相对隶属度大于0.5的过程，即发生干旱，故正游程的长度称为干旱历时t，阴影部分是连续干旱过程中每个月的Xt的累加，记作干旱强度Z，可用来表征连续过程中干旱的强弱。相应的负游程中每个月的Xt的累加的绝对值，记作降水强度P。

图1 干旱的识别过程

2.2 干旱过程修正

在干旱的识别过程中会出现小干旱和小降水过程，小干旱过程是指出现在长历时降雨过程之后的干旱事件，如图1中的过程A，发生在降水强度较大的过程B之后，由于前期降水的影响，这样的小干旱事件A在实际过程中是不发生干旱的，故应修正。

干旱过程修正需要考虑前期的降水对当前干旱状态的影响，而旱涝过程是交替的，若k过程是干旱，那么k-1过程就是洪涝。k过程的前期降水影响系数，可用k-1过程的降水强度与k过程的干旱强度之比表征。

故本文定义前期降水影响系数χk

(2)

式中：χk是第k个过程的前期降水影响系数;Zk为第k个过程的干旱强度;Pk-1为第k-1个过程的降水强度，当χk大于某一值χ时，则说明第k个过程不发生干旱。

2.3 气象干旱概率风险模型

气象干旱风险通过描述不同程度下的干旱发生概率以及干旱损失量，进而揭示其时空分布特征。游程概率理论[12-14]无需假定变量的分布特征，是从简单的游程统计现象中，揭示了游程发生的概率，广泛用于干旱的频率分析。为揭示总体概率分布特征，本文采用游程理论计算不同程度的干旱概率，并以各程度下的平均干旱强度作为干旱损失量，通过两者的乘积构造风险指数，建立气象干旱风险评价模型。

2.3.1 基于游程理论的气象干旱概率计算

(1)状态发生概率p

由于总体的状态发生概率不确定，本文采用计算样本的状态发生概率代替总体，见公式(3)。

(3)

式中：n为序列总时段数;l为状态个数;x为某指定状态下的各个游程长度，本文中对应的即各个干旱历时;g(x)为样本中干旱历时为x发生的频次。

(2)游程长度概率分布函数F(x)

根据游程概率原理[11]，游程长度不小于x的概率分布函数，见式(4)。

(4)

对于某一点α发生干旱程度为β的概率为Fαβ。

2.3.2 干旱损失量 干旱的直观体现是降水量的短缺，而干旱造成的损失归根到底是因为降水量的短缺，故本文用降水量短缺量表征区域气象干旱的损失程度，即降水量短缺程度越大，说明该区域发生气象干旱时的损失量越大。而干旱强度表征的是干旱过程中累计的降水短缺，故本文将不同程度下的平均干旱强度作为该程度下的干旱损失量S，见公式(5)。

(5)

式中：Sαβ为第α个点在干旱程度为β时的干旱损失量，干旱程度为β共有k个干旱过程;Dγ为第γ个过程的干旱强度。

2.3.3 干旱风险指数 根据风险度的定义，灾害是风险发生概率和损失量的乘积，本文用风险度表征风险指数，则对于某一点在某一程度下的气象干旱风险指数Zαβ可按式(6)计算：

Zαβ=Fαβ·Sαβ

(6)

式中：Zαβ为第α个点在干旱程度为β时的干旱风险指数。

3 淮河流域干旱风险评价实例应用研究

淮河流域位于东经111°55′～121°25′，北纬30°55′～36°36′之间，跨河南、安徽、江苏和山东4省，流域面积约27×104km2。淮河流域环山临海，地形复杂，处于中国南北气候过渡带，又受季风气候影响，气候多变，降水时空差异大，干旱灾害频发。

淮河流域干旱事件包括流域性干旱和区域性干旱，具有较为显著的空间差异性，因此本文将淮河流域分为4个部分开展研究，包括淮河上游区(王家坝以上南、北)、淮河中游区(王蚌区间南、北和蚌洪区间南、北)、淮河下游区(高天区、里下河区)、沂沭泗河区(沂沭河区、日赣区、中运河区、湖东区、湖西区)，如图2所示。本文所采用的降水数据为中国地面降水日值格点数据集，尺度为0.5°×0.5°网格，时间范围为1961 -2015年。

对淮河流域107个格点，通过月降水距平百分率和月连续无雨日数两个指标构造干旱点和非干旱点，并采用可变模糊评价方法计算对于干旱的综合相对隶属度。

根据对立统一定理，以对干旱的综合相对隶属度X0=0.5进行干旱的识别，接着取χ=10，经干旱过程修正得到修正后的干旱过程，并作为干旱风险分析的基础。

为便于进行不同程度下的气象干旱风险分析，本文按干旱历时将淮河流域的气象干旱分为以下5个程度：小于3个月、3～6个月、6～9个月、9～12个月和12个月以上。

对修正后的干旱过程进行频率分析，采用游程理论计算5种干旱程度的发生概率，并绘制淮河流域5种干旱程度的概率分布图，如图2。

由图2可知，淮河流域在不同程度下干旱发生概率以3个月为界限，呈现两种不同的分布规律。干旱历时小于3个月时，流域干旱发生概率呈现由东南向西北逐渐减小的规律，其中“王蚌区间南岸”的南部和“王蚌区间北岸”西部的小部分地区概率最高，超过了0.75，而“王蚌区间北岸”的北部以及“湖西区”的西北部地区概率最低，在0.50以下。干旱历时大于3个月时，规律则相反，从东南向西北逐渐增加，尤其是“王蚌区间北岸”的北部地区以及“湖西区”的西北部，发生3个月以上干旱的概率始终高于其它地区，这说明流域西北较东南更易发生长历时干旱。

本文将降水量的短缺作为区域气象干旱的损失量，而降水量的短缺可用平均干旱强度表征，将5种不同干旱程度下的平均干旱强度作为该干旱程度下的干旱损失量，并绘制淮河流域在5种干旱程度下的干旱损失量分布图，如图3。由图3可以看出，淮河流域干旱损失量在不同干旱程度下的规律基本一致，由东南向西北逐渐增加。干旱历时大于3个月时，从“王蚌区间北岸”北部向东延伸经“湖西区”北部、和“湖东区”北部至“沂沭河区”北部的一片区域干旱损失量较大，其中“湖西区”北部至“沂沭河区”北部的区域干旱损失量最大。在干旱历时小于3个月时，干旱损失量较大的地区集中在“王家坝以上北岸”的北部、“王蚌区间北岸”大部分地区和“湖西区”东部、“湖东区”西部。

将不同程度下干旱发生概率与干旱损失量的乘积作为该程度下的干旱风险指数。并对该指数应用自然断点法，这是一种常用的基于数字统计规律的分级方法，卢晓宁等[15]将该法应用至干旱风险的分级分类评价中，本文同样采用此法将不同程度下的气象干旱划分成5个等级(表1)。

表1 气象干旱灾害风险等级划分

图2 淮河流域不同气象干旱程度下概率分布图

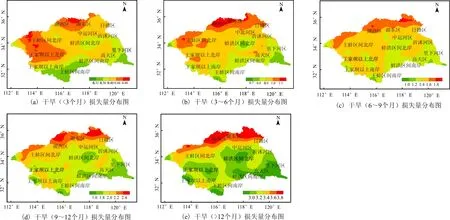
图3 淮河流域不同气象干旱程度下干旱损失量图

根据干旱风险等级划分绘制淮河流域5种干旱程度的风险指数分布图，如图4。对比图4(a)～4(e)发现，干旱历时小于3个月时，流域的干旱风险大致符合由东南到西北逐渐增加的规律，尤其是“王蚌区间北岸”的北部地区和“湖西区”的西北部地区，历时在3～6个月时，风险指数大于0.327，历时在6～9个月时，风险指数大于0.173，历时在9～12个月时，风险指数大于0.084，历时在大于12个月时，风险指数大于0.080，在同等程度下相比于流域其他区域始终处于高风险地带，需要重点防范。在发生小于3个月的干旱时，流域的东北部 ——“湖东区”和“沂沭河区”北部与流域的西南部——“王家坝以上南岸”的北部和“王家坝以上北岸”的南部地区风险较高。

图4 淮河流域不同气象干旱程度下风险指数分布图

4 结 论

本文针对气象干旱问题，基于可变模糊理论，建立了气象干旱风险评价模型。并以淮河流域为例进行气象干旱风险评价，主要结论如下：

(1)淮河流域在不同程度下的干旱发生概率以3个月为界限，呈现两种不同的分布规律。干旱程度较低(历时小于3个月)时，流域干旱发生概率由东南向西北逐渐减小；干旱程度较高(历时大于3个月)时，流域干旱发生概率由东南向西北逐渐增加。

(2)淮河流域干旱损失量在不同干旱程度下的规律基本一致，呈现由东南向西北逐渐增加的规律。

(3)干旱程度较低(历时小于3个月)时，流域风险高风险带在西南部和东北部，干旱程度较高(历时大于3个月)时，流域气象干旱风险由东南到西北逐渐增加，尤其是“王蚌区间北岸”的北部地区和“湖西区”的西北部地区，始终处于高风险地带。

[1] 顾 颖,刘静楠,林 锦.近60年来我国干旱灾害特点和情势分析[J].水利水电技术,2010,41(1):71-74.

[2] 黄会平.1949-2007年全国干旱灾害特征、成因及减灾对策[J].干旱区资源与环境,2010,24(11):94-98.

[3]OKADAN,TATANOH,HAGIHARAY,etal.Integratedresearchonmethodologicaldevelopmentofurbandiagnosisfordisasterriskanditsapplication[J].DisasterPreventionResearchInstituteAnnuals,KyotoUniversity, 2004,47(C):1-8.

[4] 冯 波,章光新,李峰平.松花江流域季节性气象干旱特征及风险区划研究[J].地理科学,2016,36(3):466-474.

[5] 王 莺,王劲松,姚玉璧.甘肃省河东地区气象干旱灾害风险评估与区划[J].中国沙漠,2014,34(4):1115-1124.

[6]TOBINGA,MONTZBE.Naturalhazards:explanationandintegration[M].NewYork:TheGuilfordPress,1997.

[7] 杜 云,蒋尚明,金菊良，等.淮河流域农业干旱旱灾风险评估研究[J].水电能源科学,2013,31(4):1-4.

[8] 孙 鹏,张 强,邓晓宇，等.塔里木河流域干旱风险评估与区划[J].中山大学学报(自然科学版),2014,53(3):121-127.

[9] 陈守煜,王子茹.基于对立统一与质量互变定理的水资源系统可变模糊评价新方法[J].水利学报,2011,42(3):253-261+270.

[10] 李 敏,陈守煜,王运涛，等.基于可变集的汛期分期多指标识别方法[J].水利学报,2013,44(12):1420-1424.

[11] 雷江群,黄 强,王义民,等.基于可变模糊评价法的渭河流域综合干旱分区研究[J].水利学报,2014,45(5):574-584.

[12] 杨好周,梁忠民,胡义明，等.游程理论在云南省干旱重现期分析中的应用[J].水电能源科学,2013,31(12)：8-12.

[13] 李天水,王 顺,庄文化，等.游程理论和Copula函数在二维干旱变量联合分布中的应用[J].干旱区资源与环境,2016,30(6):77-82.

[14] 马秀峰,夏 军.游程概率统计原理及其应用[M].北京：科学出版社,2011.

[15] 卢晓宁,洪 佳,王玲玲，等.复杂地形地貌背景区干旱风险评价[J].农业工程学报,2015,31(1):162-169.