混凝土中硫酸根离子扩散系数劣化效应研究

马晏骏， 陈党生， 孙忠民， 丁凯伦

(上海理工大学 环境与建筑学院, 上海 200093)

1 研究背景

在混凝土被硫酸盐腐蚀过程中，硫酸根离子与混凝土材料的水化产物发生化学反应造成混凝土内缺陷变化，决定了混凝土硫酸根离子扩散具有时变性，通常体现在混凝土中硫酸根离子扩散系数随着时间的变化而变化。

Tumidajski等[1]利用Fick第二定律建立了硫酸根离子浓度及扩散深度随时间变化的关系理论模型；Gospodinov等[2]提出了通过混凝土的抗压强度和空隙率来确定硫酸根离子在混凝土中扩散程度的方法；赵顺波等[3]考虑了混凝土硫酸根离子的吸收能力对混凝土硫酸根离子扩散系数的影响，结合实验建立了混凝土硫酸根离子浓度预测模型；梁咏宁等[4]通过实验提出了不同水灰比下扩散系数随腐蚀时间变化经验公式；徐惠[5]考虑了混凝土的水胶比、溶液腐蚀浓度、养护时间和应力比的综合影响，给出了硫酸盐在混凝土中的有效扩散系数的计算公式。关于描述化学产物如何影响硫酸根离子的扩散过程的研究相对较少。

另外，由于混凝土材料是一种非均匀性材料，虽然文献[6-10]基于Fick第二定律对混凝土硫酸根离子扩散模型进行了修正，但上述研究都是建立于假定混凝土中的孔隙分布是均匀的基础上，因此，需要进一步考虑随机因素的影响。

本文综合考虑了化学腐蚀产物和混凝土材料的非均匀性对扩散的影响，引入扩散系数的化学反应劣化效应系数，分别研究建立混凝土硫酸根离子的确定性扩散理论模型和随机性扩散理论模型。

2 实 验

2.1 实验设计

试样为100 mm×100 mm×100 mm的细石混凝土，水泥为上海建筑材料集团水泥厂生产的425号硅酸盐水泥，细骨料为天然河砂，细度模数为3.0，粗骨料为5～10 mm连续级配的碎石。具体配合比见表1。

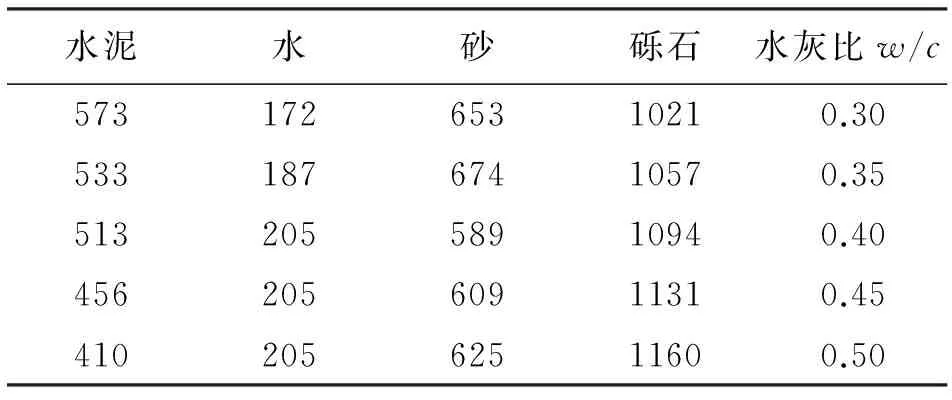
表1 混凝土配合比设计 kg/m3

2.2 试样成型及实验步骤

试样成型24 h后脱模，标准条件养护28 d后取出晾干,选择其中一面为工作面,其他5个面用环氧树脂密封。将密封好的试件工作面朝上浸泡在浓度为10%的硫酸钠溶液中，保证液面高出试件顶面至少10 mm，并且每20 d更换新溶液。在腐蚀龄期分别为1、3、5、7和9个月时，用钻头直径为30 mm的钻孔机在混凝土试件工作面正中心取深度为0～4、4～8、8～12、12～16、16～20 mm 5个深度层混凝土粉样，并用孔径为0.63 mm的方孔筛过筛。同一水灰比下的5个试件平行取样，同一水灰比下同一深度层上的5个试件粉末作为该层的代表样品，对上述样品按照中华人民共和国国家标准制盐工业通用实验进行处理[11]，并分析样品中硫酸根离子的含量。用上述方法测得的同一水胶比下同一深度层上的5个试件粉末的硫酸根离子的含量取平均值，作为该深度层上硫酸根离子含量的平均值。

3 实验结果分析

混凝土中硫酸根离子一维扩散分析理论通常以Fick第二定律为基础：

(1)

方程(1)的初始条件为t=0，x>0时，c=c0；边界条件为x=0，t>0时，c=cs。在此初始和边界条件下，解方程(1)可得：

(2)

式中：c0=0； cs=6.76%；c(x,t)为任意腐蚀时间内任意截面硫酸根离子浓度，%；t为腐蚀时间，s；x为截面到暴露面的距离，mm；Dt为t时刻的扩散系数，mm2/s； erf为误差函数。

将实验测得的不同腐蚀时间下混凝土工作面上0～4 mm深度层上硫酸根离子含量的平均值c(x,t)，代入公式(2)可以求得混凝土硫酸根离子的扩散系数的平均值随着腐蚀龄期变化规律，见图1。

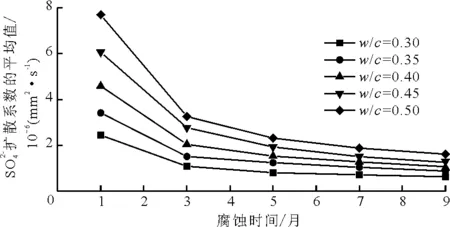
图1 SO42-扩散系数平均值变化规律

由图1可知混凝土硫酸根离子的扩散系数的平均值随着腐蚀龄期的增加而减小，下面结合硫酸根离子腐蚀过程中混凝的微观结构变化对该现象加以分析。

梁咏宁等[12]通过扫描电镜(ScanningElectronMicroscope，SEM)试验，观察浸泡于浓度为10%的硫酸钠溶液中混凝土试样，图2为观察到的SO42-不同腐蚀龄期的混凝土SEM照片。从图2中可看到，当未受到硫酸根离子腐蚀时，混凝材料内部有大量的初始孔隙，腐蚀时间为3个月时在孔隙中能看到少量的针状钙矾石和块状石膏结晶积聚，当腐蚀到6个月时孔隙中有大量的石膏晶体。

上述现象表明，酸根离子向混凝土内部扩散的过程中与混凝土材料水化产物发生化学反应生成钙矾石、石膏等晶体，随着腐蚀龄期的增加，腐蚀产物结晶会在孔隙中累积，使得混凝土的孔径分布向小孔方向移动。因此，硫酸根离子的扩散系数会随着腐蚀龄期的增加而减小。

图2 SO42-不同腐蚀龄期混凝土SEM照片

4 扩散理论模型

4.1 扩散确定性理论模型

为了描述腐蚀产物对混凝土硫酸根离子扩散系数的影响，参照类似于损伤力学中定义损伤变量的方法，引进一个关于扩散系数的化学反应劣化效应系数Kche。

在混凝土硫酸根离子侵蚀膨胀密实阶段(见图3(a)、3(b))，其初始的空隙横截面积为A0。由于化学反应生成的腐蚀产物使截面的一部分被腐蚀产物填充，设被填充的面积用Ache表示。当把混凝土当成均匀性材料时，可以假设初始状态下的微孔隙在混凝土各个方向均匀分布且所有孔隙大小相同。因此，可定义扩散系数的化学反应劣化效应系数为：

(3)

由公式(3)可知，在腐蚀初期混凝土内部的水化产物还没有与硫酸根离子发生化学反应或者由于腐蚀时间太短没有生成腐蚀填充产物，此时Kche=0。随着腐蚀龄期的增加，腐蚀产物的填充面积Ache不断增加，Kche→1。因此在混凝土硫酸根离子侵蚀膨胀密实阶段Kche介于0～1。

图3 硫酸根离子侵蚀过程

当空隙被填满以后，由于化学反应的持续进行，多余的产物会对孔隙壁产生挤压作用，造成混凝土内部孔隙产生开裂，此时进入混凝土硫酸根离子侵蚀膨胀开裂阶段(见图3(c)、3(d))。在该阶段由于有新的裂缝，初始扩散通道的面积变为eA0，其中e为初始扩散通道的放大系数(e≥1)。

在膨胀密实阶段，设t0时刻，混凝土内部孔隙的初始截面A0为硫酸根离子的初始扩散通道，此时对应的扩散系数为D0，由于化学反应产生的腐蚀产物的填充作用，腐蚀龄期为t时硫酸根离子的扩散通道变为A0-Ache，t时刻的扩散系数Dt可表示为：

(4)

在膨胀开裂阶段，t时刻对应的扩散通道面积为eA0-Ache，该阶段的扩散系数Dt可表示为：

(5)

(6)

其中，在膨胀密实阶段由于没有受到膨胀开裂的影响，此时e=1。随着腐蚀反应的持续进入膨胀开裂阶段，此时e>1。将公式(6)代入公式(1)，能够导出考虑化学反应因素影响的硫酸根离子确定性扩散新方程：

(7)

方程(7)的初始条件和边界条件同方程(1)，在此初始和边界条件下，解得混凝土硫酸根离子扩散的确定性理论模型如下：

(8)

4.2 扩散随机性理论模型

扩散的确定性理论模型是建立在假定混凝土材料为均匀性材料的基础上。但是在实际情况中，混凝土材料是一种典型的非均匀性材料，文献[13]认为混凝土材料在其形成之初就具有随机分布的微孔洞、微裂缝等初始缺陷。文献[12]中通过扫描电镜实验(SEM)观察浸泡于10%的硫酸钠溶液中6个月时的试件，局部可见贯通的裂缝(见图2(d))。

上述研究充分说明了硫酸根离子在混凝土中的初始扩散通道A0，无论是在初始状态还是后续的开裂演化都不可避免的具有随机性。因此，D0和Dt均是随机变量，此时考虑化学反应因素影响的随机性扩散系数Dt可表示为：

Dt=(e-Kche)D0

(9)

(10)

方程(10)的初始和边界条件同方式(1)，在此初始和边界条件下，解得混凝土硫酸根离子随机性扩散模型如下：

c=c0+(cs-c0)·

(11)

5 扩散理论模型讨论

5.1 理论模型中和Kche的取值

梁咏宁等在文献[4]中根据实验拟合得到不同水灰比下，扩散系数随腐蚀时间变化的经验公式：

D=(18.9w/c-3.08)T-0.72×10-6

(12)

式中：D是硫酸根离子的扩散系数，mm2/s；w/c是混凝土的水灰比；T是腐蚀时间，月。

当不考虑膨胀开裂的影响时(e=1)，将T0=1代入公式(12)可求得不同水灰比下模型中的参数的取值，见表2。

表2 模型中参数取值

5.2 理论模型与试验数据比较

分别用扩散确定性理论模型方程式(8)和扩散随机性理论模型方程式(11)计算得到的结果和实验数据作对比，见图4、5。

从图4中可以看到，利用混凝土硫酸根离子确定性扩散模型计算得到的数值与实验结果吻合的较好，较为准确地反映了硫酸根离子平均浓度的变化规律。所以，考虑化学反应因素影响的硫酸根离子扩散确定性理论模型可以预测任意腐蚀时间下扩散进入到混凝土中不同深度的硫酸根离子含量的平均值。

图4 混凝土中硫酸根离子浓度方程(8)计算结果和实测值的对比

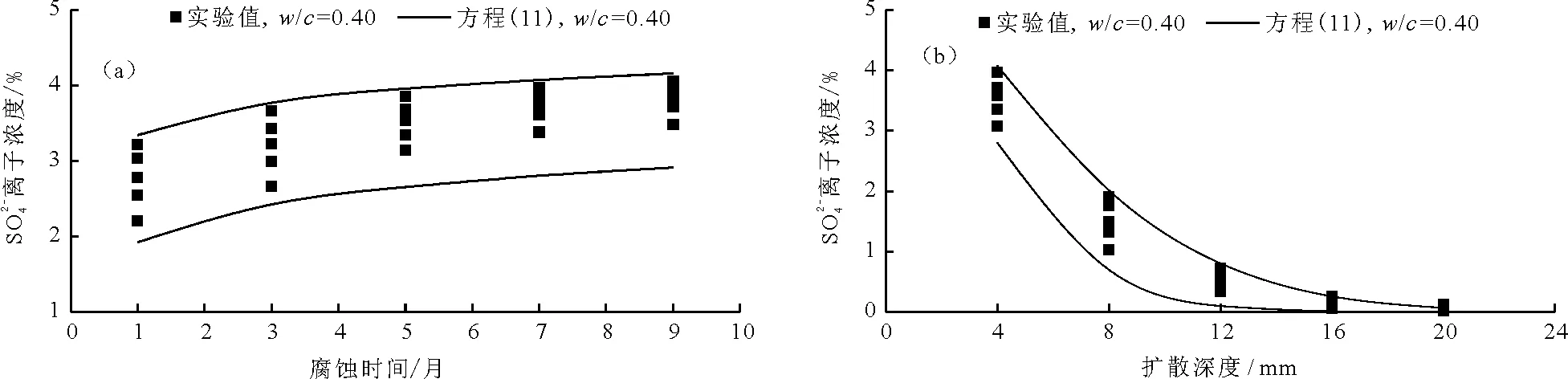
图5 混凝土中硫酸根离子浓度方程(11)计算结果与实测值对比

从图5中可以看出，实验结果全部落在随机性预测模型的范围之内，较精确反映了混凝土硫酸根离子浓度的变异性。所以，考虑化学反应因素影响的混凝土硫酸根离子随机性扩散理论模型可以较好地预测出任意腐蚀时间和任意深度层上硫酸根离子浓度的范围。

6 结 论

(1)在Fick第二扩散定律的基础上，充分考虑化学反应因素对混凝土材料内部缺陷的影响， 引进Kche，经过严密的推导确定了Kche的取值范围在0～1之间，建立了考虑化学反应因素影响的混凝土硫酸根离子扩散确定性理论模型。

(2)在确定性扩散理论模型的基础上，充分考虑了混凝土材料初始缺陷具有随机性的特点，建立了考虑化学反应因素影响的混凝土硫酸根离子扩散随机性理论模型。

(4)通过混凝土硫酸根离子扩散确定性理论模型和实验结果比较，表明确定性理论模型可以很好地预测出不同腐蚀时间和不同腐蚀深度上的硫酸根离子浓度的均值。

(5)通过混凝土硫酸根离子扩散随机性理论模型和实验结果比较，表明随机性理论模型可以很好地预测出不同腐蚀时间和不同腐蚀深度上的硫酸根离子浓度分布范围。

[1]TUMIDAJSKIPJ,CHANGW,PHILIPOSEKE.Aneffectivediffusivityforsulfatetransportintoconcrete[J].Cement&ConcreteResearch, 1995, 25(6):1159-1163.

[2]GOSPODINOVP,KAZANDJIEVR,MIRONOVAM.Theeffectofsulfateiondiffusiononthestructureofcementstone[J].Cement&ConcreteComposites, 1996,18(6):401-407.

[3] 赵顺波,杨晓明. 受侵蚀混凝土内硫酸根离子扩散及分布规律试验研究[J]. 中国港湾建设,2009(3):26-29+53.[4] 梁咏宁,王 佳,孔海新,等.混凝土硫酸根离子扩散系数的研究[J].混凝土,2011(3):11-13.

[5] 徐 惠.硫酸盐腐蚀下混凝土损伤行为研究[D].徐州：中国矿业大学,2012.

[6] 侯绍雯,魏 杰,孟 烁,等.基于侵蚀损伤演化机理的硫酸根离子扩散模型[J].绿色环保建材,2017(7)：244.

[7] 张 柬,浦 海,张连英.硫酸盐在混凝土中扩散过程研究[J].徐州工程学院学报(自然科学版),2012,27(2):57-62.[8] 高子瑞,李淑娥,金明东,等.修正的混凝土内硫酸根离子迁移模型研究[J].科学技术与工程,2016,16(19):97-101.

[9] 张 凯,陈亮亮,侍克斌,等.不同取代率再生骨料混凝土硫酸根离子扩散试验[J].科学技术与工程,2016,16(31):275-280.

[10] 陈记豪,钱晓军,赵顺波.干湿循环-硫酸盐作用的混凝土中硫酸根离子分布预测[J].河南科学,2008,26(7):815-817.

[11] 国家技术监督局，GB/T130258-91 制盐工业通用试验方法硫酸根离子的测定[S].北京：中国标准出版社，1991.

[12] 梁咏宁,袁迎曙.硫酸钠和硫酸镁溶液中混凝土腐蚀破坏的机理[J].硅酸盐学报,2007,35(4):504-508.

[13] 李 杰.混凝土随机损伤力学的初步研究[J].同济大学学报(自然科学版),2004,32(10):1270-1277.

[14] 杨绿峰,胡春燕,陈 正,等.混凝土中氯离子随机时变扩散过程及浓度分布[J].建筑材料学报,2013,16(2):210-216.

[15]LEFEBVREM.BasicProbabilityTheorywithApplications[M].NewYork:Springer,2009.

[16] 燕彩蓉,张青龙,赵 雪,等.基于广义高斯分布的贝叶斯概率矩阵分解方法[J].计算机研究与发展,2016,53(12):2793-2800.