搅拌器水下转轮安装高度优化数值模拟

魏文礼， 娄威立， 张泽伟， 刘玉玲

( 西安理工大学， 陕西 西安 710048)

1 研究背景

在食品、化学、生物等生产过程中，搅拌反应器得到广泛应用，其内部流场的研究对于节约成本、优化体型设计、提高运行效率等具有重要的意义。对搅拌反应器的研究，国内外学者做了大量的工作，主要方法有实验研究和数值模拟方法，以及两者相结合的方法。Yoon等[1]对一个带转盘的单叶轮搅拌槽进行了大涡模拟，得出：水流从叶片射向搅拌槽内壁，漩涡的扩散和能量的耗散广泛分布，通过增加转速和减小分子扩散，能量耗散较低的区域将减小；Busciglio等[2]对单层六直叶片连续通气搅拌槽内流场及气液混合过程进行了大涡模拟，得出：提高转速可以明显减少混合时间，对低转速下不同位置的流场进行精确分析有利于搅拌槽性能的改善；Stryjewski等[3]采用实验的方法对搅拌反应器内的流场进行了研究，得出：增加转轮转速对搅拌器内液体流速影响显著，在叶轮区域速度呈线性变化；梁瑛娜等[4]对双层六直叶涡轮桨、双层六斜叶涡轮桨以及双层六直斜叶交替涡轮桨搅拌槽流场进行研究，得出：3种桨型的流场结构均为四涡环流模式,速度极值出现在叶端附近；Song等[5]对双层六直叶涡轮桨搅拌槽内气液两相流动进行数值模拟，得出：增加搅拌转速或减小通气量有利于气体在搅拌槽内掺混和分散；刘玉玲等[6]对搅拌槽内气液流动进行了大涡数值模拟的研究，得出：随着转速的增大，径向速度和轴向速度也随着增大，对气液搅拌器采用大涡模型进行模拟要比k-ε紊流模型更加准确； Sajjadi等[7]对单层六直叶涡轮桨搅拌器进行了实验和数值模拟研究，得出：输入功率相同时,靠近搅拌桨区域的流速较大,而远离搅拌桨区域的流速较小，当搅拌桨叶片离底距离较高时，六直叶涡轮搅拌槽内流动倾向于径向流动；张庆华等[8]在湍流流场数值计算的基础上，通过求解示踪剂的浓度输运方程，得出：随着搅拌转速的增大，相同体积分数对应的混合时间逐渐减小，利用适宜的尺寸和安装位置可有效降低混合时间；朱桂华等[9]对偏心双轴搅拌槽进行了数值模拟，发现偏心双轴搅拌槽可以打破中心搅拌的流场对称性，消除隔离区并且流场内各方向的速度分量比中心搅拌槽的大，速度梯度明显增大，搅拌混合区明显增大，得出了偏心双轴搅拌槽更利于搅拌槽内气液两相混合的结论；徐金等[10]研究了桨叶直径、叶片角度、挡板宽度等结构参数的改变对搅拌槽内混合过程的影响；付勤民等[11]研究了偏心率的改变对双层搅拌槽内流场的影响，发现了偏心距与搅拌槽内的速度最大值不是简单的线性关系，偏心距在速度最大值时某一范围内最大，筒体内流体的混合效果最佳；李志刚等[12]重点研究了不同桨叶高度和转速下搅拌槽内的流动特性以及时均流速分布的特性，得到了针对研究对象下的最优桨叶高度与最优转速；郭聪聪等[13]用数值模拟的方法研究了挡板对搅拌效果的影响，重点研究了挡板系数的改变对搅拌功率的影响；施阳和等[14]研究了三角形挡板和长方体空心挡板形状下搅拌槽内流场的变化情况；黄男男等[15]研究了在有无导流筒的条件下，搅拌槽内流场及速度的改变情况，得出了在有导流筒的条件下，可以有效减少搅拌槽内功率消耗的结论；樊梨明等[16]研究了双层搅拌槽内桨叶间距的改变对流速特性以及搅拌功率的影响。

以往的研究中大都选择固定的转轮安装高度来研究搅拌槽内流场特性、混合时间和含气率等参数，而对单层桨搅拌器在不同转轮安装高度下的流场、含气率分布、混合时间等的研究较少。本文采用RNGk-ε紊流模型对一个单层气液搅拌器进行数值模拟，分析了搅拌器内不同叶轮安装高度对速度场、气含率等的影响。

2 数学模型

RNGk-ε二方程模型在处理高应变率和流线曲率较大的流动方面效果较好,并且具有经济合理、稳定、高精度等优点，因此在目前流场的各种模拟计算中广泛应用。描述水流的质量守恒方程、动量守恒方程和RNGk-ε紊流模型，详细内容见文献[17-18]。根据实际情况，将文献[17-18]中的数学模型施加合理的边界条件后，可以求得各未知变量，如流速、水体体积率函数、紊动动能、压力以及紊动耗散率等的分布情况。

3 计算区域与边界条件

3.1 计算区域及网格

采用的搅拌槽模型如图1(a)所示，搅拌槽半径为R=0.08m，高H=0.25m。叶片尺寸长0.018m，宽0.002m，厚0.0128m。中心转轴直径为0.005m，为了对网格进行更好的划分，将通气孔设于底部，直径为0.001m，叶片区域采用分块画网格的方法。计算网格总数为179 700。内部区域网格与叶片典型网格如图1(b)、1(c)及1(d)所示。

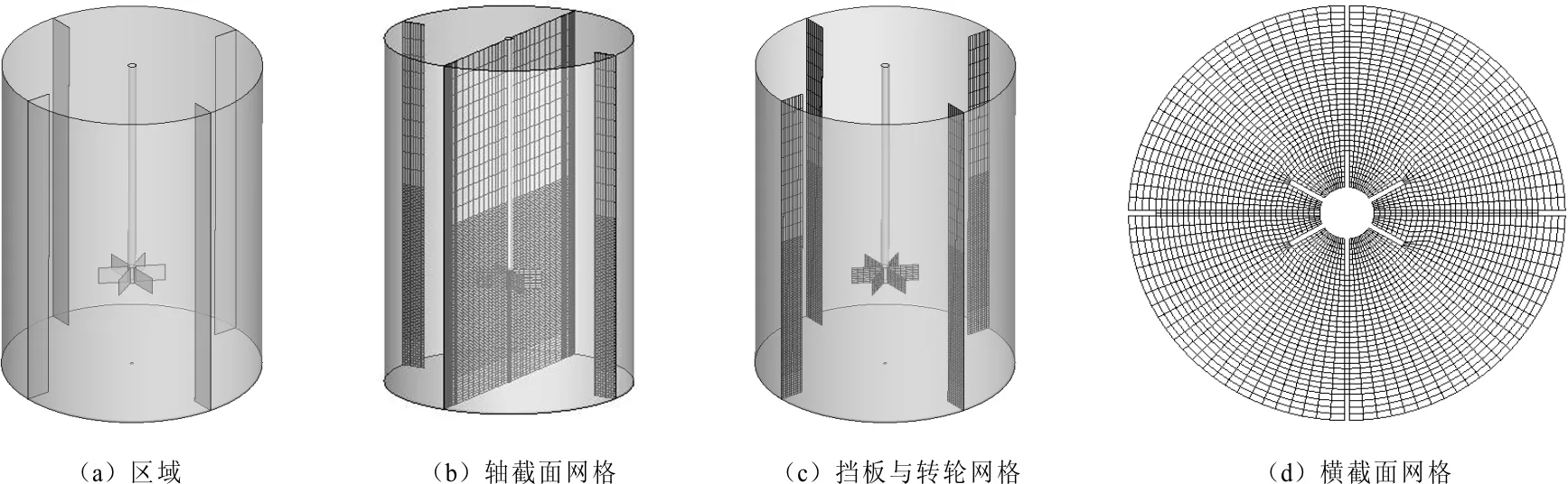
图1 计算区域及计算网格

3.2 边界条件

通气孔进口边界定义为速度入口，气流速度为0.5m/s。叶片区域利用多参考系法处理，流体流动类型设定为定常流动，叶轮转速为450r/min。分别设计安装高度为10%H(0.025m)、20%H(0.050m)、30%H(0.075m)、40%H(0.100m)、50%H(0.125m)、60%H(0.150m)进行计算。采用无滑移旋转边界来处理叶片，旋转速度为0，采用标准壁面函数来处理底面与壁面，顶面为压力出口边界。控制方程传送项采用速度压力耦合的SIMPLE算法，离散格式采用二阶迎风，所有残差收敛标准均为10-4。计算采用的时间步长为0.005s,计算总时间为250s时，结果收敛。

4 计算结果分析

4.1 流场分布分析

图2为转轮安装高度在10%H～60%H情况下六直叶涡轮搅拌槽内流场的布局情况。从模拟结果图2(a)～2(f)可以看出，单层六直叶涡轮产生的流线沿轴线对称分布，最大速度位于叶片首部，因此叶轮首部附近的流动比较剧烈。径向射流在流动过程中拖带周围流体一起运动，射流与槽壁碰撞后，一部分沿边壁向上运动，另一部分向下流向槽底部。射流到达液面或槽底后，流动沿径向回流到轴中心，接着分别向下或向上回流到叶轮区。这样在每个叶轮的上下方各形成一个涡环。

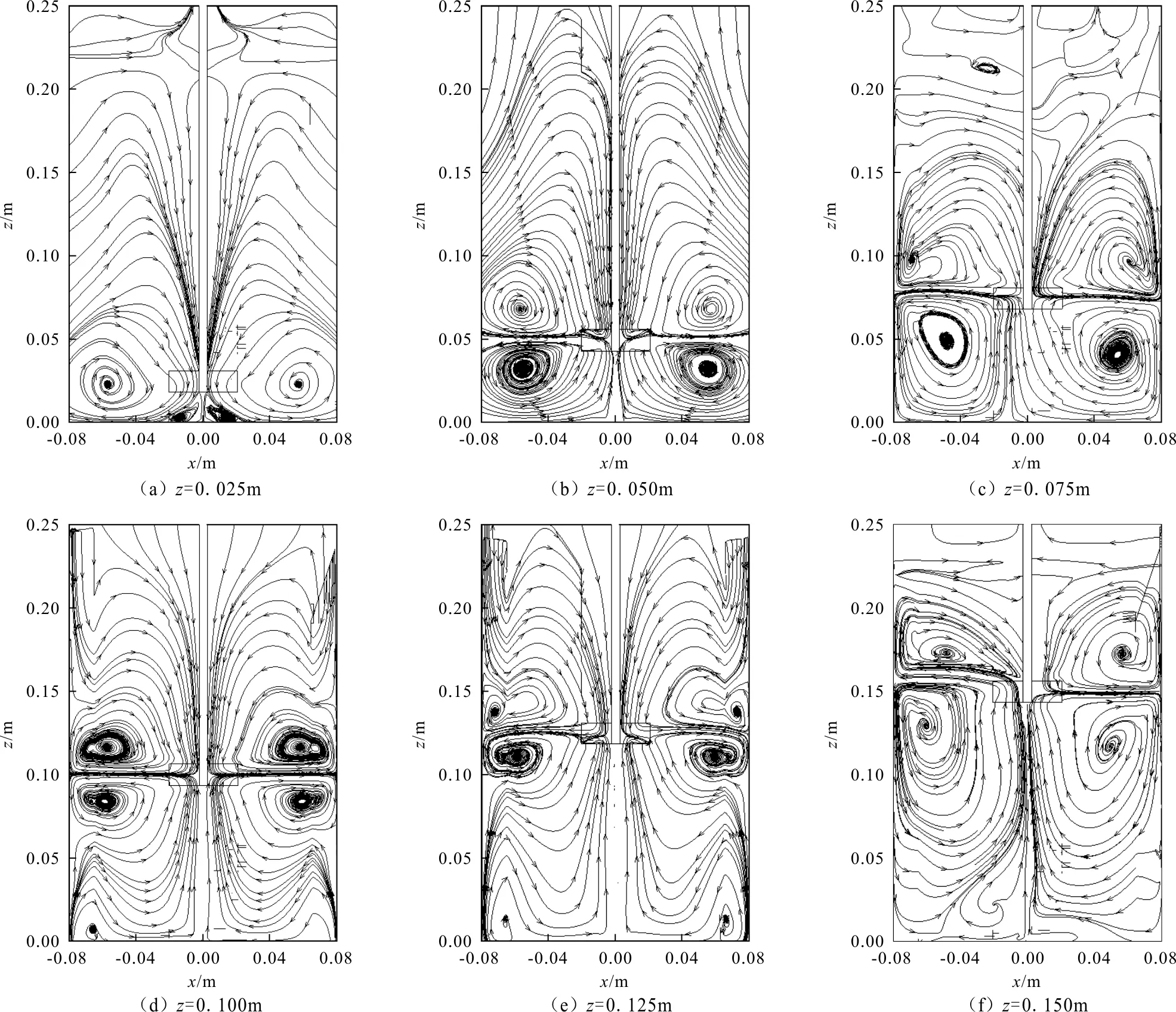
图2 流线图

图2(a)、2(b)与2(c)、2(d)、2(e)的流动形式差别明显。在安装高度低于20%H时，槽内流动倾向于轴向流动，“双循环”流型中的下循环涡流区被抑制，仅在靠近桨叶轴心区域形成一个小循环区。随着桨叶安装高度的增加，流动逐渐从轴向流转化为径向流，在安装高度靠近中间部位时，“双循环”流型中的上下循环流动区都是充分发展的径向流动，当安装高度达到60%H时，槽内流动又倾向于轴向流动。说明当安装高度小于20%H和高于60%H时，单层六直叶涡轮搅拌槽流动形式较20%H～60%H不同，槽内流动倾向于轴向流动。

搅拌槽轴对称位置上竖线速度分布如图3所示，由图3可知搅拌槽内竖线速度基本呈轴对称分布。因此、可以采用轴对称面上的流动特征来表征整个搅拌器内的流动特性。

4.2 速度沿竖线分布的分析比较

沿径向分别取R=0.02m、R=0.04m及R=0.06m处轴向液体竖线速度分布情况如图4所示。

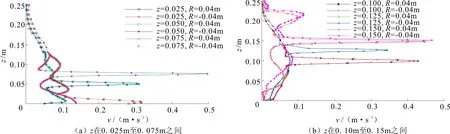
图3 对称位置竖线流速比较图

图4 速度沿竖线分布

从图4中可以看出：(1)不同安装位置的速度曲线比较相似，在转轮径向上下方都出现了液体环流。离开转轮位置，速度出现小幅度波动，离搅拌桨较远的位置处的流速有明显减小。也就是说，搅拌桨输入的能量大多耗散在搅拌桨附近，而远离搅拌桨的流体没有得到很好的混合；(2)随着转轮安装高度的增加，最大速度之间略有差异，安装高度在50%H(0.125m)时最大，60%H(0.150m)时最小；(3)沿径向各转轮附近的流速均有所减小，在靠近转轴区域各转轮附近的速度大于挡板附近区域。

图5为不同转轮安装高度搅拌槽内液体的平均速度。由图5可知在转轮安装高度为50%H(0.125m)位置速度出现一峰值，其值明显大于其他安装高度的速度，表明当转轮安装高度在中间位置时，槽内液体易获得较大流速，同时有利于带动搅拌槽内液体的流动。当转轮安装高度低于30%H(0.075m)时，搅拌槽内的平均速度比安装高度为60%H(0.150m)时的速度略高，但增幅较小。说明转轮安装高度较高时(60%H)相对于较低时不利于流体的流动，但过高和过低的安装高度都不利于带动槽内液体流动。

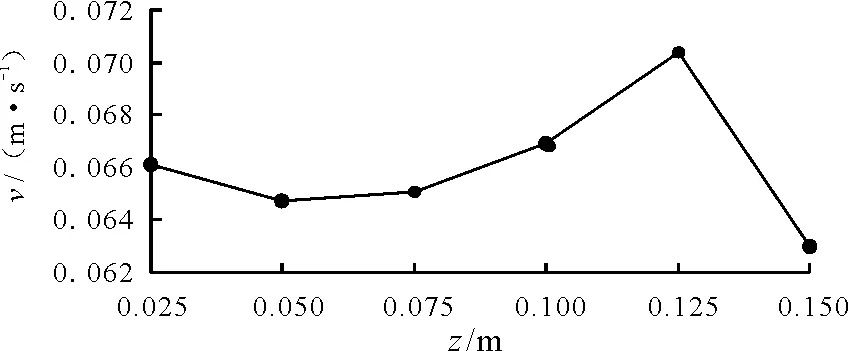
图5 不同转轮安装高度槽内液体的平均速度

4.3 含气率分析

4.3.1 轴线含气率 图6为同一转速下、转轮不同安装高度，沿竖线的含气率分布。由图6可以看出，含气率在搅拌槽内分布并不均匀。当安装高度在50%H(0.125m)时，远离液面区域的含气率高于相对应的其他安装高度的含气率。而在液面附近处的含气率比较深处位置的含气率低。原因可能是：当安装高度较高时，在液面附近区域，上部漩涡强度较大，对出口边界的空气具有较强的卷吸作用，易形成较大尺寸的气泡，大气泡的浮力大，很容易克服重力和流体的干扰到达液面逸出，平均停留时间变短，不利于气液之间的混合。而离液面较远的区域，大尺寸的气泡在液面附近区域立即溢出，而大量小尺寸的气泡却由于惯性力的作用被流体带向搅拌槽的中下部，平均停留时间变长，有利于气液之间的混合。当安装高度较深时，在液面附近区域，上部漩涡强度较小，对出口边界的空气的卷吸作用变弱，形成的气泡尺寸变小，而小气泡却易随流体一起流动，在槽内返混多，平均停留时间长，气体得到了更充分的混掺。而在离液面较远区域，由于卷吸作用变弱，吸入的空气量较少，大多都在液面附近区域掺混。进入深处区域的空气很少，故含气率较低。安装高度在60%H(z=0.150m)时，离液面较远区域的含气率低于安装高度在50%H(z=0.125m)处，可能是由于转轮安装高度较高时不利于带动该区域液体流动，只有小部分小气泡在液流的夹带下向槽中下部运动，气泡在浮力的作用下克服惯性力并上升，使得含气率在此区域较低。图7为转轮在不同安装高度时搅拌槽内的平均含气率，由图7可知，安装高度在50%H位置时含气率最高，对槽内气液二相之间的混掺更有利。

4.3.2 混合时间 混合时间是指将两种物理和化学性质不同的流体，通过搅拌使之相互溶合，达到规定混合浓度所需要的时间。习惯上采用当浓度达到最终稳定浓度值的±5%以内并不再超出时，该时刻即为混合时间[8]。在不同的安装高度下，计算模型所得到的混合时间，分别为10%H为89s、20%H为83s、30%H为79s、40%H为76s、50%H为74s、60%H为79s，说明随着转轮安装高度的增加，混合时间先减小后增大，在安装高度为50%H时混合时间最小。可能是因为在此位置，两个循环漩涡在搅拌槽的中心区域直接相互作用，在上下环流之间有更快的动量和能量交换，使湍动效率增加。因此与其他安装高度相比，转轮安装在中间位置时混合时间最小。

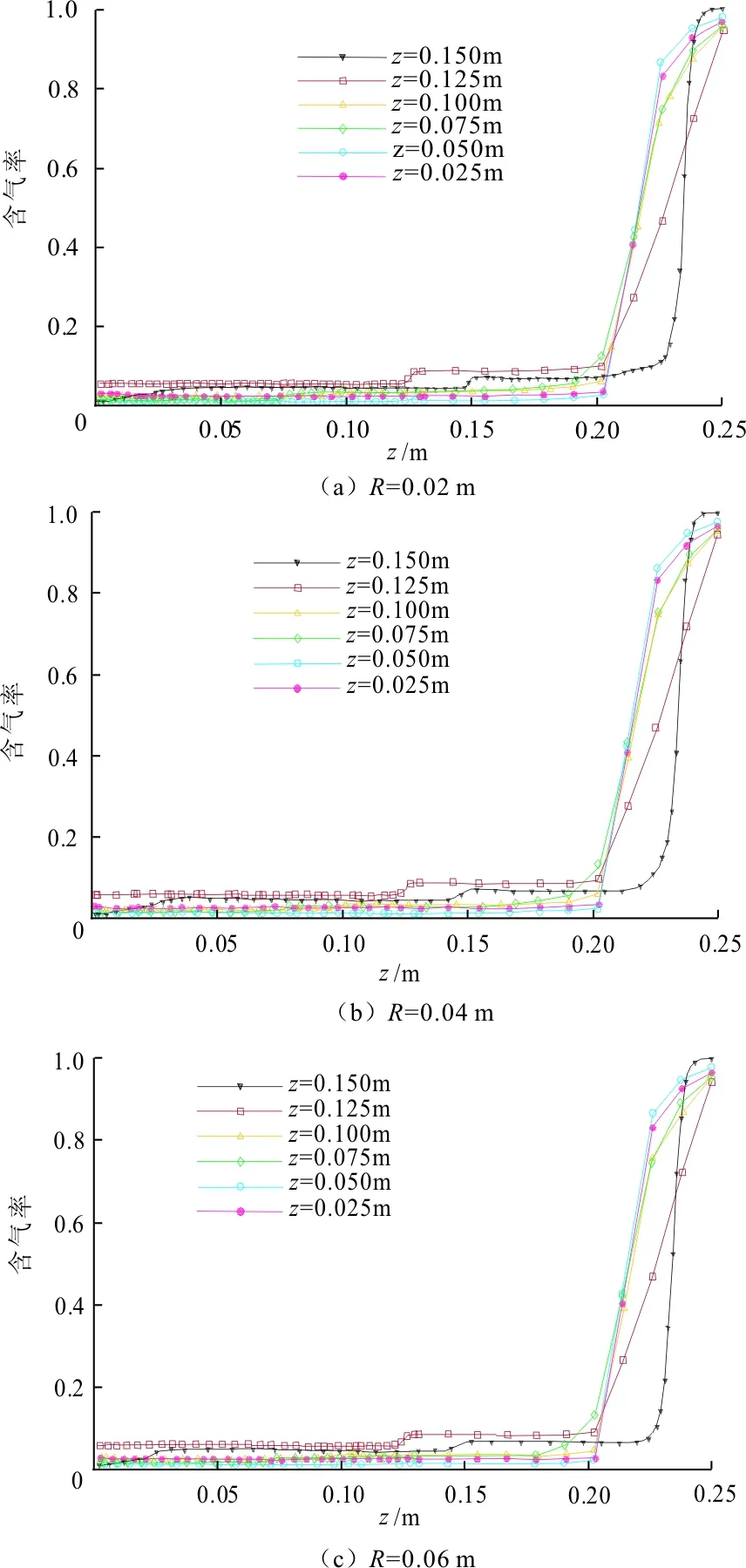
图6 同一转速下、转轮不同安装高度含气率沿竖线分布

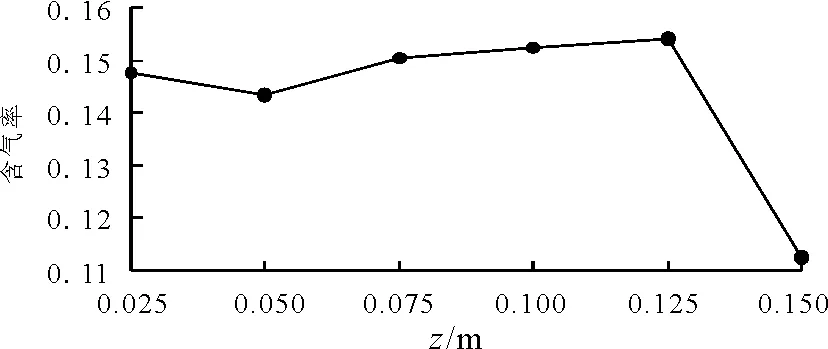
图7 不同转轮安装高度的平均含气率

4.4 功率准数

功率准数的值由模拟结果通过公式NP=P/(ρN3d5)计算，其中d为转轮直径,m;N为叶片转速,r/min;P=2πN·M为搅拌桨的搅拌功率,W;M为搅拌桨所受的总扭矩,N·m。具体计算结果见表1。

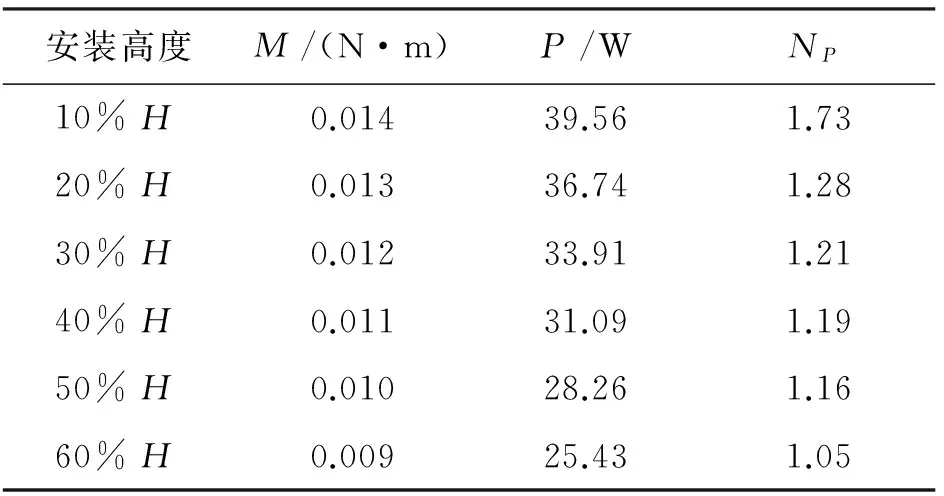
表1 功率准数计算表

由表1可知，随着安装高度的增加搅拌槽所消耗的功率、功率准数均有所减小，说明安装高度过低将使搅拌槽内所消耗的能量增加。

5 结 论

利用Fluent6.3对单叶轮气液搅拌器进行了数值模拟。采用RNGk-ε紊流模型结合多参考系法进行了模拟。计算得到了在通气量一定的情况下转轮安装高度分别为10%H(0.025m)、20%H(0.050 m)、30%H(0.075m)、40%H(0.100m)、50%H(0.125m)、60%H(0.150m)时的速度场，以及不同轴向位置的含气率。模拟结果表明：

(1)安装高度靠近中间部位时，“双循环”流型中的上下循环流动区都为充分发展的径向流区，安装高度小于20%H,或高于60%H时，单层六直叶涡轮搅拌槽流动形式发生变化，槽内流动更偏向于轴向流动。

(2)转轮安装高度在中间位置时，槽内液体较易获得较大流速，更容易带动槽内液体的流动。随着安装高度的增加，搅拌槽所消耗的功率、功率准数均有所减小。

(3)转轮安装高度对搅拌器内含气率有影响，当搅拌桨安装在槽中间位置50%H(0.125m)时，搅拌槽内含气率最高,混合时间最小，更有利于搅拌槽内气液两相之间的掺混，可提高搅拌槽运行效率。

由于搅拌器内流体流动的不稳定性，对其流动特性的精确研究还需要结合相关实验进行进一步的探索。

[1]YOONHS,BALACHANDARS,MANYH.Largeeddysimulationofpassivescalartransportinastirredtankfordifferentdiffusivities[J].InternationalJournalofHeatandMassTransfer, 2015,91:885-897.

[2]BUSCIGLIOA,MONTANTEG,PAGLIANTIA.Flowfieldandhomogenizationtimeassessmentincontinuously-fedstirredtanks[J].ChemicalEngineeringResearchandDesign,2015,102:42-56.

[4] 梁瑛娜，高殿荣.双层直斜叶及其组合桨搅拌槽三维流场数值模拟[J].机械工程学报，2008，44(11)：290-297.

[5]SONGT,JIANGK,ZHOUJ,etal.CFDmodellingofgas-liquidflowinanindustrialscalegas-stirredleachingtank[J].InternationalJournalofMineralProcessing, 2015, 142(10):63-72.

[6] 刘玉玲，赵小军，魏文礼. 搅拌槽内气液流动大涡数值模拟研究[J]. 应用力学学报，2014，31(3)：381-386+489-490.

[7]SAJJADIB,RAMANAA,IBRAHIMS.Acomparativefluidflowcharacterisationinalowfrequency/highpowersonoreactorandmechanicalstirredvessel[J].UltrasonicsSonochemistry,2015(27):359-373.

[8] 张庆华，毛在砂，杨 超，等. 一种计算搅拌槽混合时间的新方法[J].化工学报，2007，58(8)：1891-1896.

[9] 朱桂华,张丽欣,王万斌,等.偏心双轴搅拌用于污泥搅拌混合的数值模拟[J].环境工程学报,2017,11(5):3128-3134.

[10] 徐 金,逄启寿,郜飘飘,等.双层桨搅拌槽的混合过程研究[J].中国有色冶金,2017,46(1):46-49.

[11] 付勤民,周勇军,陶兰兰,等.偏心率对双层搅拌桨偏心搅拌槽内流场的影响[J].轻工机械,2016,34(5):12-16.[12] 李志刚,贾慧芳,王 健.不同搅拌参数的双层浆搅拌槽三维流场数值模拟[J].有色金属(冶炼部分),2013(7):54-60.

[13] 郭聪聪,赵恒文,许 卓,等.搅拌槽内挡板对搅拌效果的数值模拟[J].给水排水,2011,47(S1):199-202.

[14] 施阳和,赵 进.两种不同挡板的双层桨搅拌槽三维流场数值模拟[J].化工机械,2014,41(2):211-214+231.

[15] 黄男男,石秀东,张建华,等.导流筒对搅拌槽流场的影响[J].食品与机械,2009,25(1):93-96.

[16] 樊梨明,李庆生.双层桨搅拌槽内流动特性的CFD研究[J].食品与机械,2016,32(1):84-86.

[17] 周俊波，刘 洋.FLUENT6.3流场分析从入门到精通[M]. 北京：机械工业出版社, 2012.

[18] 魏文礼，戴会超. 紊流模型理论及工程应用[M]. 西安: 陕西科学技术出版社, 2006.