从概念教学出发，浅谈数学核心素养在日常教学中的渗透与思考

黄利娜

（苏州工业园区星湾学校，江苏 苏州）

随着教育部《关于全面深化课程改革落实立德树人根本任务的意见》的颁布，数学核心素养得到明确，即具备数学基本特征，适应学生终身发展和社会发展的必备品格和关键能力，也是数学课程目标的集中体现。素养需要在长期的教育中慢慢养成，如何将数学核心素养渗透到日常教学中，使之逐渐成为学生自身的品格和能力，是在实践层面上的一个关键性问题。

概念教学是整个中学数学教学过程中的一个重要环节，是学生进一步学习数学定理、法则、方法以及提高数学能力的基础。笔者试从概念教学出发，浅谈数学核心素养在日常教学中的渗透与思考，以期与同仁们共同探索与交流。

一、概念的引入——溯本求源，灌溉“数学知识树”

数学概念是揭示现实世界空间形式和数量关系本质属性的一种思维形式。引入数学概念就是揭示概念发生的实际背景和基础，了解它的必要性与合理性，初步揭示它的内涵、外延，给概念下定义。一般可以通过以下途径引入数学概念。

1.生活情境引入

数学来源于生活，又广泛应用于生活，合理创设生活情境引入概念，是联系数学和实际生活的纽带。例如，苏科版八年级上册“6.1函数”，笔者这样设计：

陶行知先生说过：“脱离生活的教育是鸟笼的教育。”在日常教学中，部分教师省去创设情境引入概念这一环节，强行将概念“灌输”给学生，这是一种急功近利的做法，不但割裂了数学与生活间密不可分的联系，长此以往，甚至会抹杀学生学习数学的兴趣和欲望。因此，合理创设生活情境引入概念，有利于培养学生抽象思维和建模能力，同时也有利于激发学生的学习兴趣，为概念的进一步理解和应用奠定基础。

2.数学情境引入

从学生实际出发，把握概念与概念之间的联系，合理创设数学情境，能有效帮助学生较快速了解概念，理清概念在相应知识体系中的内涵和外延，对如何进一步研究新知有简要的分析和预判。

创设数学情境，主要有两类——“生长型”和“类比型”。“生长型”，即新概念，犹如大树枝节处又生出新枝杈，本质上是由熟悉的概念“长”出来的，教师只需搭好问题的“脚手架”供学生攀登。例如，对任意平行四边形增加条件——“有一个角是直角”，便引入矩形，或增加条件——“有一组邻边相等”，即可得菱形等。那么，研究平行四边形的思想方法，当然也适用于由它衍生出的新图形，即可引导学生自主探索研究，培养学生的几何直观和创新意识。“类比型”，即许多概念之间存在相似之处，教师可以从它们的内在异同切入，类比引入新概念。例如，用“分数”引入“分式”的概念，用“全等三角形”引入“相似三角形”的概念，用“圆心角”引入“圆周角”的概念等。这不但使学生更加明确概念的具体定义，也将学生置身于整个知识体系中，感受到数学是一颗枝繁叶茂的大树，生命力旺盛，血脉经络间互联互通。

《义务教育数学课程标准（2011年版）》建议：从学生实际出发，创设有助于学生自主学习的问题情境，引导学生通过实践、思考、探索、交流等，获得数学的基础知识、基本技能、基本思想、基本活动经验，促使学生主动地、富有个性地学习，不断提高发现问题和提出问题的能力、分析问题和解决问题的能力。

在日常教学过程中，以上两类概念引入形式，并不是孤立存在的，教师应根据教学内容，关注学生学情，因材施教，培养学生“既知其然，还要知其所以然”，做到溯本求源。

二、概念的形成——行成于思，再探概念之真谛

概念引入后，学生对于概念的定义有了初步了解，但并未达到理性认识，形成科学概念，还必须引导学生运用抽象思维挖掘概念的本质属性，逐步建立清晰的概念体系。例如，苏科版九年级上册“2.1圆”，笔者这样设计：

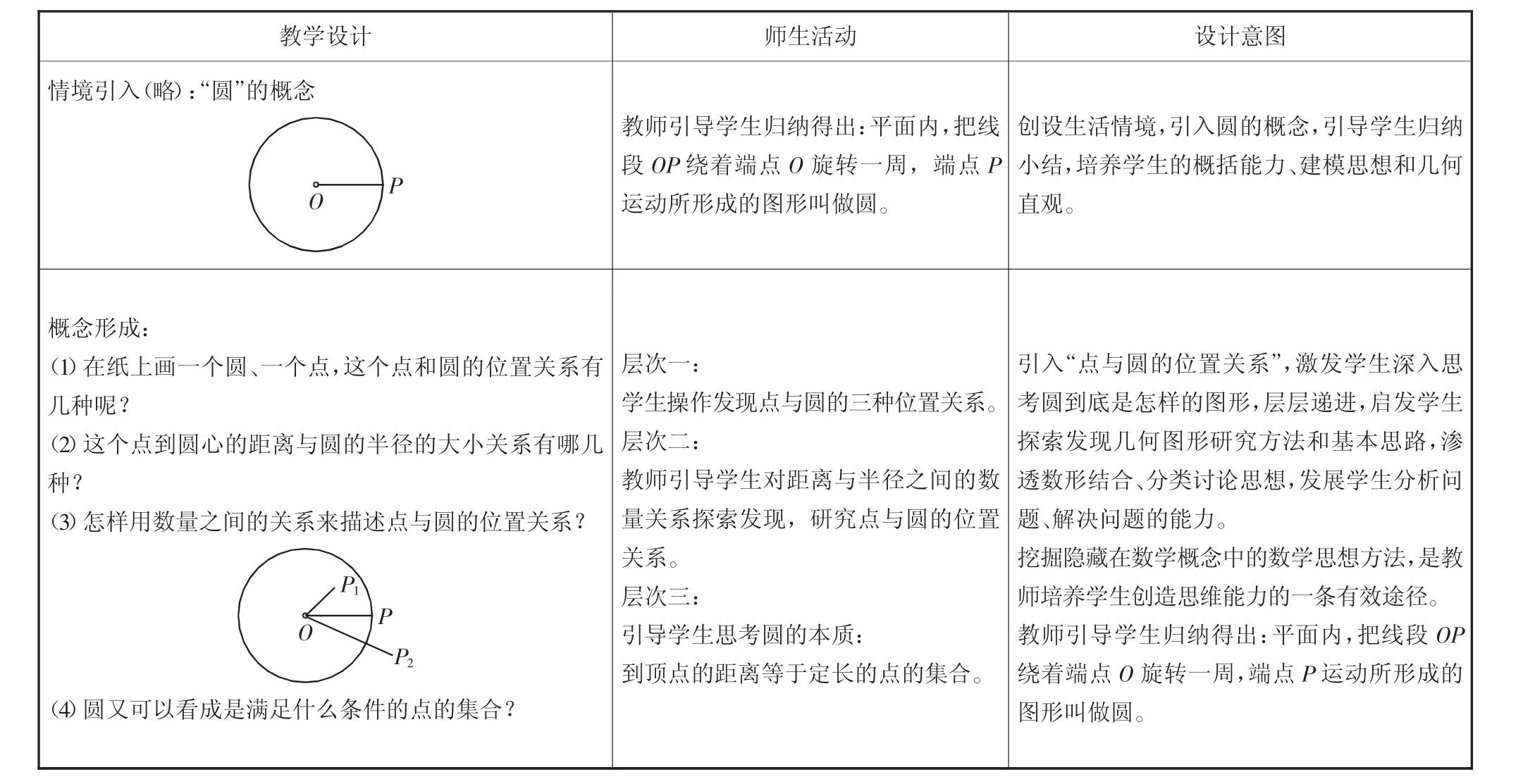
教学设计 师生活动 设计意图情境引入（略）：“圆”的概念P教师引导学生归纳得出：平面内，把线段OP绕着端点O旋转一周，端点P运动所形成的图形叫做圆。创设生活情境，引入圆的概念，引导学生归纳小结，培养学生的概括能力、建模思想和几何直观。概念形成：（1）在纸上画一个圆、一个点，这个点和圆的位置关系有几种呢？（2）这个点到圆心的距离与圆的半径的大小关系有哪几种？（3）怎样用数量之间的关系来描述点与圆的位置关系？P P2层次一：学生操作发现点与圆的三种位置关系。层次二：教师引导学生对距离与半径之间的数量关系探索发现，研究点与圆的位置关系。层次三：引导学生思考圆的本质：到顶点的距离等于定长的点的集合。（4）圆又可以看成是满足什么条件的点的集合？引入“点与圆的位置关系”，激发学生深入思考圆到底是怎样的图形，层层递进，启发学生探索发现几何图形研究方法和基本思路，渗透数形结合、分类讨论思想，发展学生分析问题、解决问题的能力。挖掘隐藏在数学概念中的数学思想方法，是教师培养学生创造思维能力的一条有效途径。教师引导学生归纳得出：平面内，把线段OP绕着端点O旋转一周，端点P运动所形成的图形叫做圆。

赞可夫曾说过：“教会学生思考，这对学生来说，是一生中最有价值的本钱。”引导学生经历概念的形成过程，并在此过程中思考概念的本质，从整体上、从内部规律上把握概念所反应的对象，让学生主动建构数学知识，发展创造思维，提升数学素养。

三、概念的内化——触类旁通，“数学是玩概念的”

李邦河院士说：“数学根本上是玩概念，不是玩技巧。技巧不足道也！”在理解概念后，大量的巩固练习对学生的思维培养、能力提升并非高效。如何使用概念、运用概念中的思想方法解决问题，促进后续的数学学习，才是概念教学的真正目的所在。例如，根据合并同类项的学习，学生能够通过观察、比较、交流认识具备共同特征的数学元素，感悟分类的重要思想。这样的数学活动经验，若能有效迁移至分式的加减法的学习，学生就能在短时间内更快、更有效地获取新知，同时也能够培养学生主动建构、解决问题的能力，这才是数学核心素养的关键所在。

在日常教学过程中，概念作为数学的基础，是数学教学的出发点。在概念教学过程中，既要关注学生的情感、实际学情，还应着眼于整个知识体系，注重概念与概念之间的关联性，处理好局部知识与整体知识的关系，启发学生主动探索数学概念的本质，培养学生主动建构、不断创新，利用数学知识解决问题的关键能力，提升数学核心素养。