强杂波环境下的LGM-PHDF算法
2018-03-16陈金广赵甜甜王明明马丽丽
陈金广,赵甜甜,王明明,马丽丽
(西安工程大学 计算机科学学院,陕西 西安 710048)
0 引 言
使用概率假设密度滤波(probability hypothesis density filter,PHDF)算法来解决多目标跟踪问题是当前的一个研究热点[1,2]。Vo等提出了两种PHD算法的实现方法,非线性环境下的序贯蒙特卡罗(sequential Monte Carlo,SMC)PHDF算法[3]及线性条件下的高斯混合概率假设密度滤波(GM-PHDF)算法[4]。为了解决上述算法无法实现对目标航迹提取的问题,有学者提出为粒子或高斯项加注标签,来实现航迹估计的算法[5-8]。该类算法虽然实现了目标航迹的估计,但同时也带来了计算量增大的问题。在PHDF中,算法的时间复杂度和量测数据量成正比,且虚假量测还会影响算法的估计性能。由于基于数据关联的目标跟踪算法使用门限技术进行量测信息的筛选[9],减少了算法的计算量。文献[10]将椭球门限运用到GM-CPHDF中,提高了计算效率。文献[11,12]将量测集合划分为存活目标量测和新生目标量测进行处理,减少了计算量。文献[13]推导出极大似然门限,并通过对量测数据进行最优分配以提高算法的状态估计性能。文献[14]通过使用门限对LGM-PHDF算法进行处理,降低了时间复杂度,算法性能得到了提高,但是忽略了衍生目标的存在,会导致衍生目标的漏估计。本文针对强杂波环境下,LGM-PHDF算法计算量大且精度下降的问题提出改进,并通过仿真实验验证改进算法的有效性。
1 LGM-PHDF
LGM-PHDF是在标准GM-PHDF的基础上,为每一个高斯项添加标签,并通过管理标签实现不同时刻目标状态之间的关联和航迹的形成及维持。
首先在初始化阶段为每一个高斯项分配唯一的标签,则强度函数、标签集合和航迹集合表示如下
(1)
T0={t1,…,tJ0}
(2)
S=∅
(3)
其中,N(·;m;P)表示均值为m协方差为P的高斯分布。w(i)表示第i个高斯项的权值,J表示高斯项个数。为每个标签设置两个变量ncon和nmiss,分别表示标签是否已形成航迹和标签对应高斯项未被检测到的步数。
在每一步的预测阶段,标签集合中的元素不仅包括上一步的存活目标标签,还包括该时刻新生目标的标签,即在预测步需要为新生目标添加唯一标签。预测得到的强度函数和标签集可表示为
vk|k-1(x)=vS,k|k-1(x)+vγ,k(x)
(4)
Tk|k-1=Tk-1∪Tγ,k
(5)
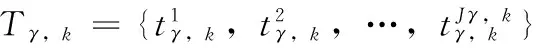
在更新步骤中,高斯项的标签不变,因此更新结束后每一个标签可能对应多个高斯项,强度函数和标签集表示如下
(6)
Tk=Tk|k-1
(7)
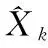
(8)
(9)
根据标签集中的标签信息对航迹进行更新和维持,步骤如下:
(1)当Tk中标签ti对应变量ncon的值为1时,该标签对应的高斯项已存在航迹。
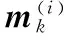
2)若Tk中有多个ti,则先将标签为ti的权值最大的高斯项状态添加到航迹Si中。然后对相同标签的高斯项权值累加,将累加和与衍生阈值wsp进行比较,判断是否有衍生目标产生。若前者大于后者则认为出现衍生目标,为权值次大的高斯项初始化标签为tj(j∉Tk),并初始化该高斯项对应目标的航迹Sj={mj}。
(2)当标签ti对应变量ncon的值为0时,为该标签创建一个新的航迹Si={mi}。
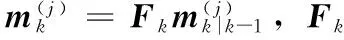
2 强杂波环境下的LGM-PHDF
传统的LGM-PHDF使用所有的量测数据对高斯项进行更新,其中与目标状态无关的量测对真实目标估计没有正面作用,且增加了系统开销。相对于GM-PHDF算法,LGM-PHDF由于增加了标签,且每一次迭代都需要对标签信息进行更新,实现了对目标航迹的估计,但在一定程度上增加了计算量。此外,当杂波密度过高时,更新的高斯项会出现权重过估计的现象,导致滤波精度的降低。
本文在预测结束后使用椭球门限对量测集合进行处理,将量测集合分为门限内与门限外两部分,认为门限内的量测是与目标状态相关的,将其用于高斯项的更新。这样就减少了参与更新的量测数量,减少了计算量,且缓解了无效量测对于高斯项权重的影响。
2.1 椭球门限
假设ε(ij)表示第i个高斯项和第j个量测的残差向量,则
(10)
(11)
椭球门限的判别式为
(12)
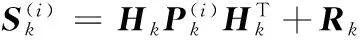
2.2 改进算法
假设k-1时刻目标的后验强度函数可表示为高斯混合的形式
(13)
预测步骤中强度函数和标签集可表示如下
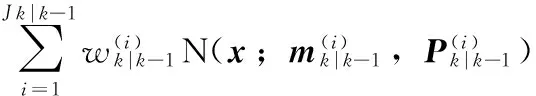
(14)
(15)
其中
(16)
(17)
(18)
(19)
(20)
(21)
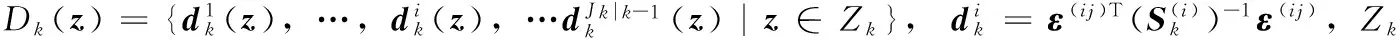
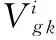
(22)
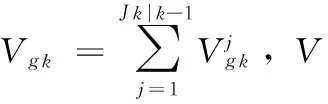
(23)
Tk|k=Tk|k-1
(24)
其中
(25)
(26)
(27)
(28)
(29)
(30)
对更新后的高斯项按照文献[4]的方法进行裁剪合并,获得状态估计,并使用LGM-PHDF标签管理机制及航迹关联方法进行航迹的管理,并获得目标运动轨迹。
3 仿真实验与结果分析
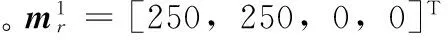
目标运动使用的系统模型为一般的线性系统模型
(31)
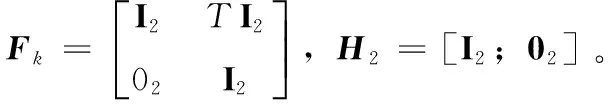
(32)
其中,Pr=diag([100,100,25,25]T)。由状态为ζ的目标产生的衍生目标的强度函数为βk|k-1(x|ζ)=0.05N(x;ζ,Qβ),其中Qβ=diag([100,100,400,400]T)。
目标的检测概率PD=0.98。观测场景中的杂波随机集Kk服从泊松分布,其强度函数为κk(z)=λVu(z),其中杂波强度λ=4.5×10-5表示单位面积杂波点的平均数目,检测区域面积为V=4×106,u(·)表示杂波在观测区域内是服从均匀分布的。仿真中,剪枝阈值Tth=10-5,合并门限U=4,允许最大高斯分布个数Jmax=200,目标提取状态阈值wth=0.5,确认消亡阈值nend=5。本实验采用最优子模式分配(OSPA)距离对算法进行评价,参数设置为p=1,c=200。
仿真结果如图1~图4所示。图1是真实量测与虚假量测的对比,图2为LGM-PHDF和本文的改进算法对目标航迹的估计,图3为LGM-PHDF算法和GM-PHDF算法以及改进算法对目标状态的估计误差,图4为3种算法对目标数目的估计。
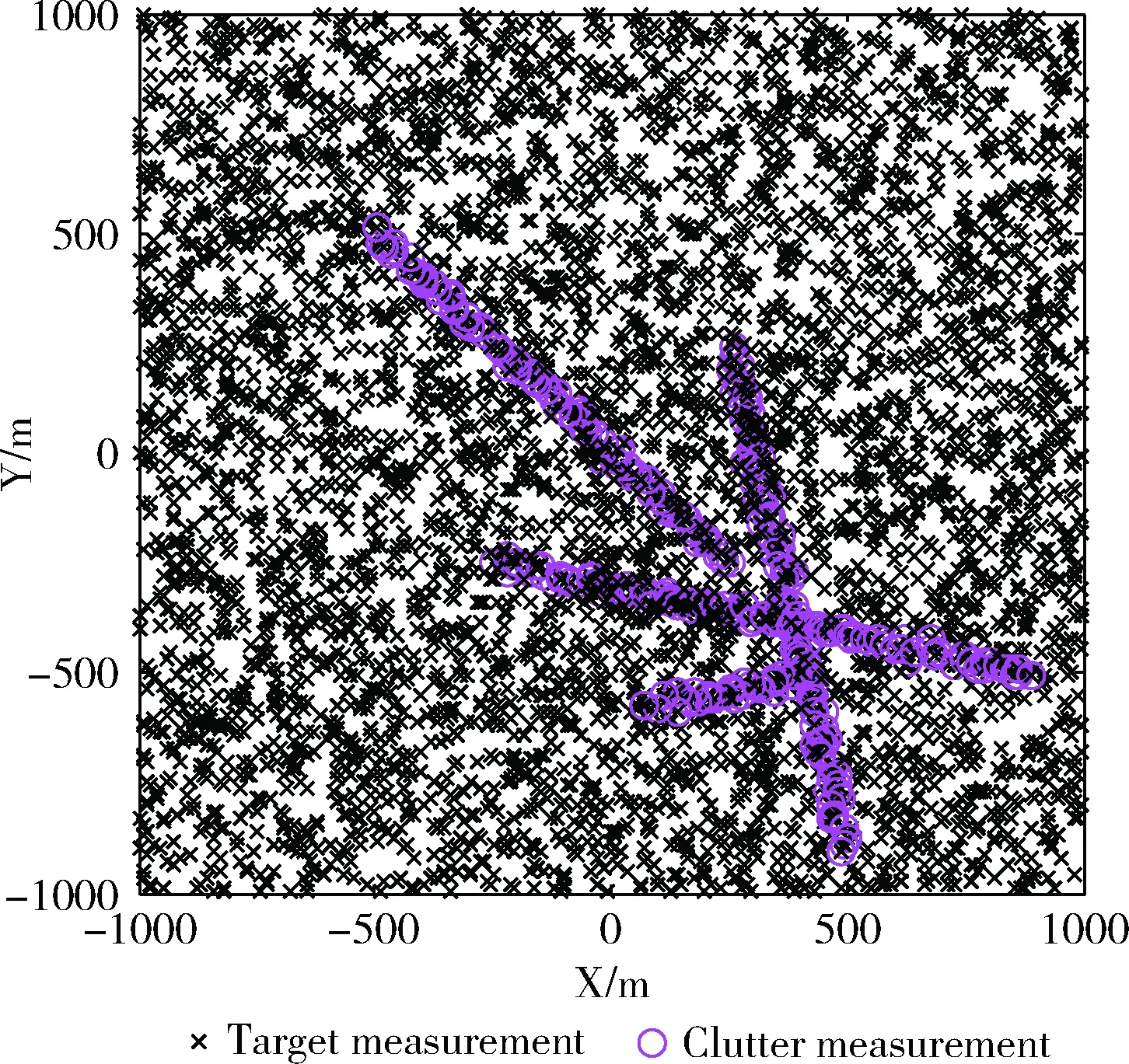
图1 目标真实量测与杂波量测
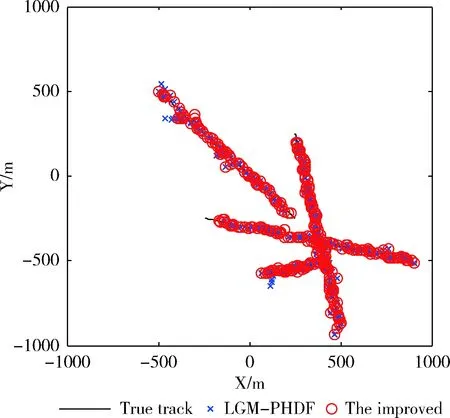
图2 目标真实运动轨迹与算法估计航迹
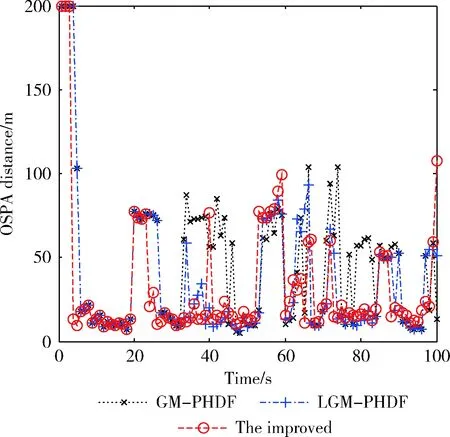
图3 算法OSPA距离
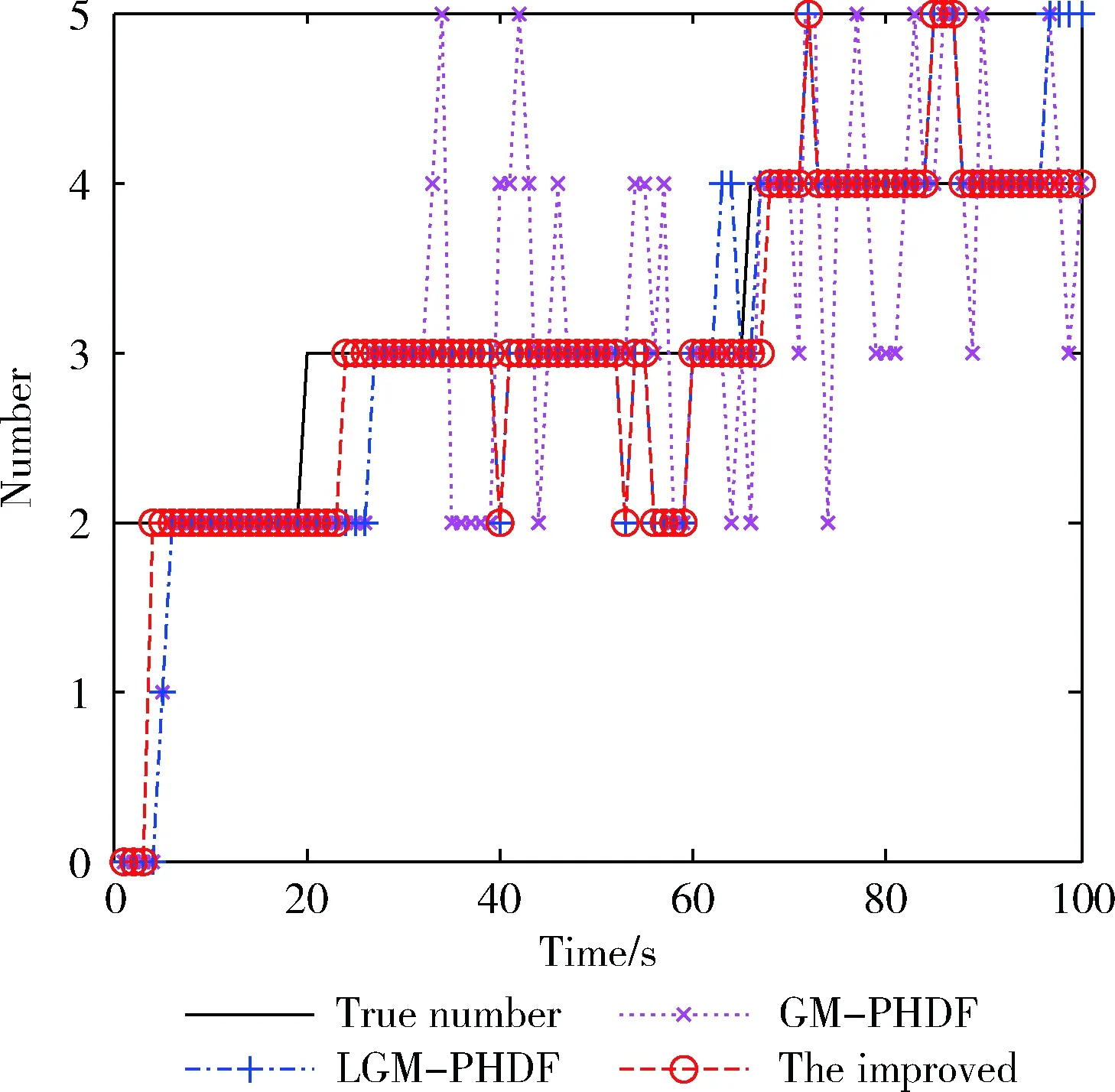
图4 目标数目估计
从图1可以看出该杂波密度下,杂波量测数量较大,会严重影响算法的运行时间与估计性能,而图2的算法估计结果可以看出,本文的改进算法可以很好地跟踪该杂波密度下的目标运动,对于目标航迹估计的误差较小。
从图3和图4的结果可以看出,相对于传统的GM-PHDF,改进算法与LGM-PHDF估计性能相对稳定,且估计性能差距不大。但是在某些时刻改进算法的估计误差更小,并且能够快速抓捕到目标状态的改变。改进算法和LGM-PHDF在第55s至第60s之间都出现了目标的漏估计,是因为第55s时目标出现交叉导致了量测数据的匹配不正确。
表1和表2分别是20次蒙特卡洛实验求得的单步平均OSPA距离及平均运行时间。可以看出,随着杂波强度的增长,GM-PHDF算法与LGM-PHDF算法的估计性能逐步下降,相应的算法运行时间却在逐步增加。然而对于改进算法,杂波强度的增长对于算法性能的影响基本可以忽略,虽然算法时间复杂度受到了杂波强度增长的影响,但是相对于其它两种算法,这些增长就显得很微小了。因此,在强杂波环境中改进算法的综合性能要比LGM-PHDF算法和GM-PHDF算法好。
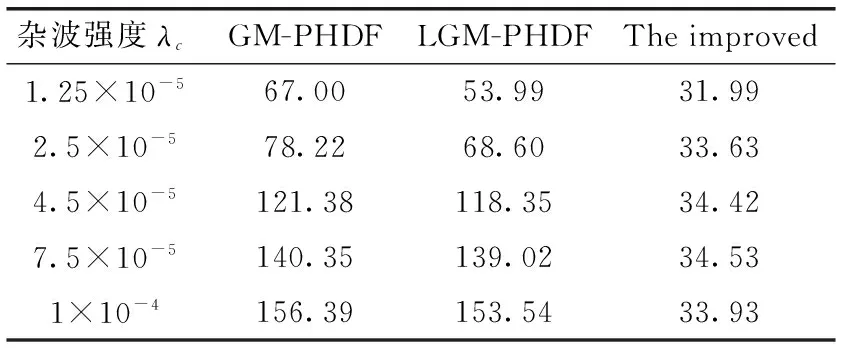
表1 平均OSPA距离/m

表2 平均运行时间/s
4 结束语
本文是对强杂波环境中LGM-PHDF的算法改进。首先在预测结束后,根据预测值与量测计算残差向量,再使用椭球门限将量测划分为有效量测和无效量测;然后在高斯项更新过程中,只使用有效量测,降低了算法的时间复杂度,同时也减缓了无效量测对目标估计性能的影响。仿真结果表明,在强杂波环境中改进算法不仅能够实现对目标航迹的提取,且在减少算法运行时间的同时提高了估计性能。但是,该改进算法在目标较接近时会出现错误估计的现象,将以此作为下一阶段的研究工作。
[1]Jian Xu,Fangming Huang, Sun Yishen,et al.Multiple target tracking based on cross sector probability hypothesis density filter in radar system[C]//14th International Conference on Control,Automation, Robotics and Vision.USA:IEEE Conference Publications,2016:1-5.
[2]Mahler R.PHD filters of higher order in target number[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(4):1523-1543.
[3]Vo B,Singh S,Doucet A.Sequential Monte Carlo methods for multi-target filtering with random finite[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1224-1244.
[4]Vo B,Ma W.The Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Single Processing,2006,54(11):4091-4104.
[5]Michael Beard,Stephan Reuter,Karl Granstrom,et al.Multiple extended target tracking with labeled random finite sets[J].IEEE Transacions on Signal Processing,2016,64(7):1638-1653.
[6]Clark D,Panta K,Vo B.The GM-PHD filter multiple target tracker[C]//Proceedings of the 9th International Conference on Information Fusion,2006:1-8.
[7]Panta K,Clark DE,Vo BN.Data association and track mana-gement for Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Aerospace and Electronic Systems,2009,45(3):1003-1016.
[8]Zhu Hongyan,Han Chongzhao,Lin Yan.Particle labeling PHD filter for multi-target track-valued estimates[C]//Proceedings of the 14th International Conference on Information Fusion,2011:1-8.
[9]Musicki D,Evans R,Stankovic S.Integrated probabilistic data association[J].IEEE Transactions on Automatic Control,1994,39(6):1237-1241.
[10]ZHANG Tao,WU Renbiao.Adaptive gating GM-CPHD filter for multitatget tracking[J].Journal of Data Acqusition and Processing,2014,29(4):549-554(in Chinese).[章涛,吴仁彪.自适应GM-CPHD多目标跟踪算法[J].数据采集与处理,2014,29(4): 549-554.]
[11]YANG Feng,WANG Yongqi,LIANG Yan.Collaborative PHD filter for fast multi-target tracking[J].System Engineering and Electronics,2014,36(11):2113-2121(in Chinese).[杨峰,王永齐,梁彦.面向快速多目标跟踪的协同PHD滤波器[J].系统工程与电子技术,2014,36(11):2113-2121.]
[12]CHEN Jinguang,QIN Xiaoshan,MA Lili.Fast GM-PHD filter for multi-target tracking[J].Computer Science,2016,43(3):317-321(in Chinese).[陈金广,秦晓珊,马丽丽.快速多目标跟踪GM-PHD滤波算法[J].计算机科学,2016,43(3): 317-321.]
[13]ZHANG Tao,LAI Ran,WU Renbiao,et al.Measurements optimal assigned GM-PHD multi-target tracking algorithm[J].Journal of Signal Processing,2014,30(12):1419-1426(in Chinese).[章涛,来燃,吴仁彪,等.观测最优分配的GM-PHD多目标跟踪算法[J].信号处理,2014,30(12):1419-1426.]
[14]Choi Mid-Eum,Seo Seung-Woo.Robust multitarget tracking scheme based on Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Vehicular Technology,2016,65(6):4217-4229.
