基于LPP-RF的基因表达数据分类
2018-03-16杨浩宇南晓斐柴玉梅
杨浩宇,南晓斐,柴玉梅
(郑州大学 信息工程学院,河南 郑州 450001)
0 引 言
基因表达数据分类问题[1]的研究目前已取得一些成果。Das等[2]使用支持向量机(support vector machine,SVM)对基因表达数据进行分类,通过实验对比了不同核函数下的分类准确率并取得了良好的分类效果。然而,当样本类别很大时,SVM计算复杂度高,且其核函数与参数设置缺乏理论指导[3];文献[4]提出了极限学习机的相异性集成算法,在基因表达数据分类上表现良好,但极限学习机的隐层节点个数需要先验知识并手工设置这些参数,节点个数不同对分类精度也会产生影响;文献[5]采用7个基因表达数据集将随机森林算法(random forests,RF)与很多传统的机器学习分类算法(如k近邻分类器、SVM以及线性判别分析等)进行比较,得出RF算法分类性能优于其它分类算法的结论。
RF算法在基因表达数据分类方面已经有了不错的性能,但是RF算法中的决策树只能产生平行于坐标轴的超巨形决策面[6]。在基因表达数据中构建决策树,通常会使得决策树庞大,对数据敏感,且分类效果也不好,因此RF算法在基因表达数据分类方面还有性能提升空间。本文受Zhang等[7]提出的集成特征空间的随机森林算法启发,将局部保持映射(locality preserving projections,LPP)与RF算法中决策树每个节点的属性空间相结合,提出基于LPP的RF算法。该算法通过LPP将决策树节点数据映射到新的属性空间中,在该属性空间中选择第一个属性就可使数据得到较好的划分结果。在9个基因表达数据集上的实验对比结果表明,本文提出的算法在分类准确率上比传统RF算法高出17%,运行时间比传统RF算法缩短了7倍,其它性能指标如Recall、Precision、G-mean等指标均有提高。
1 相关知识
1.1 随机森林算法
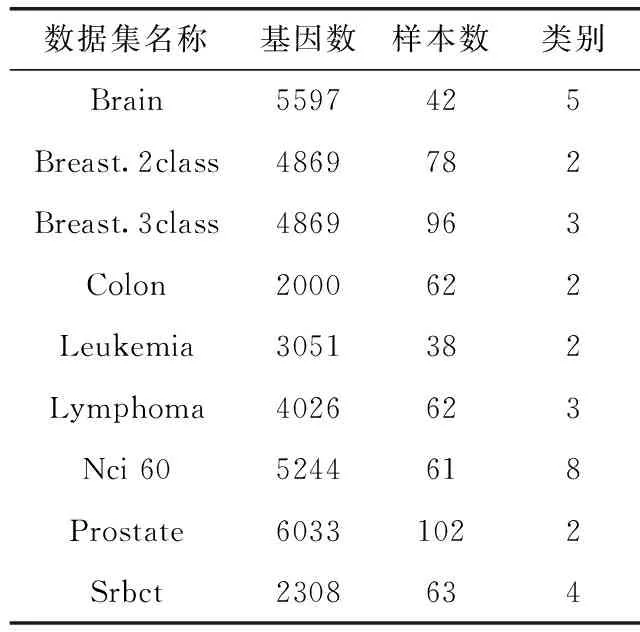
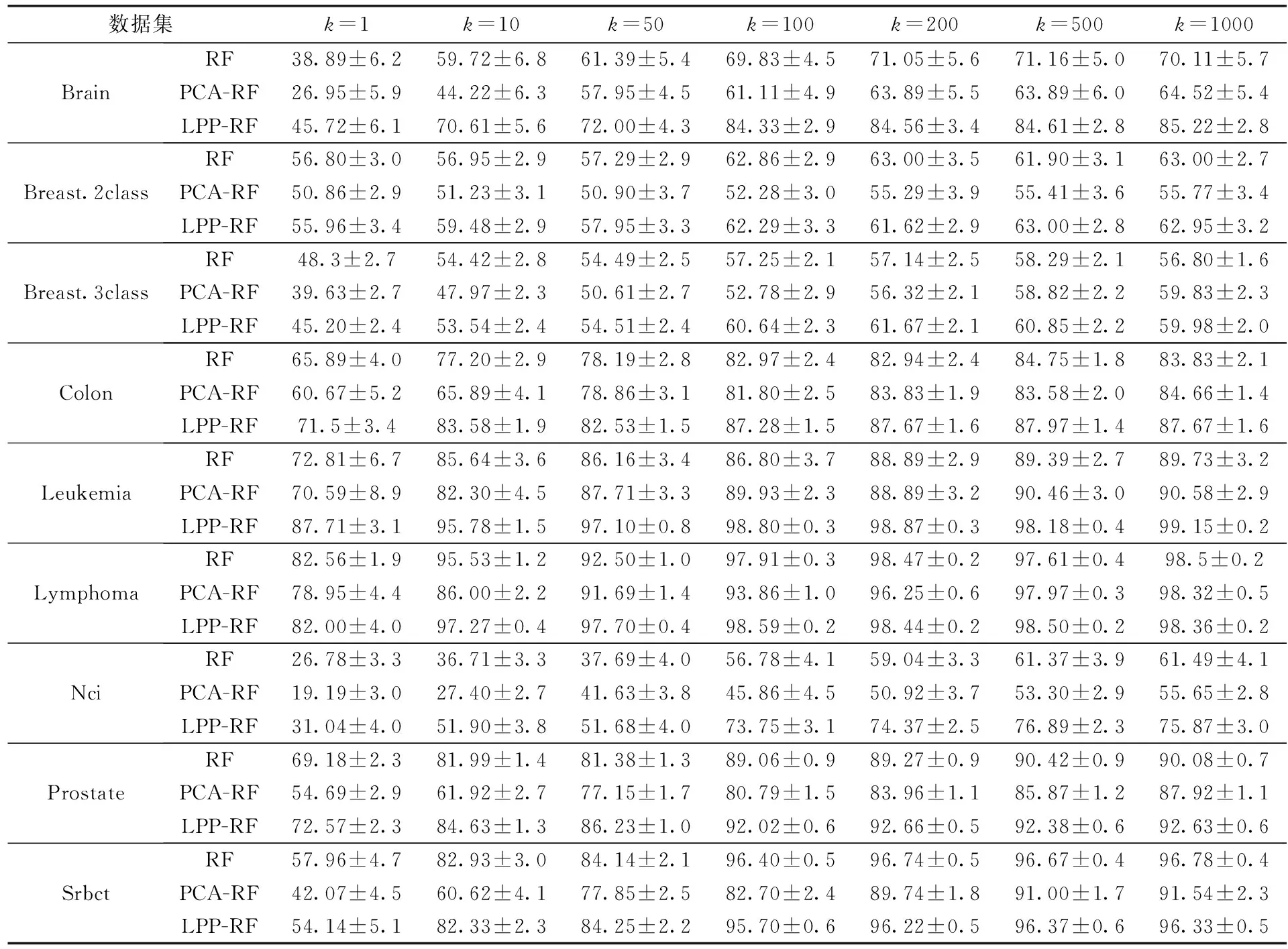
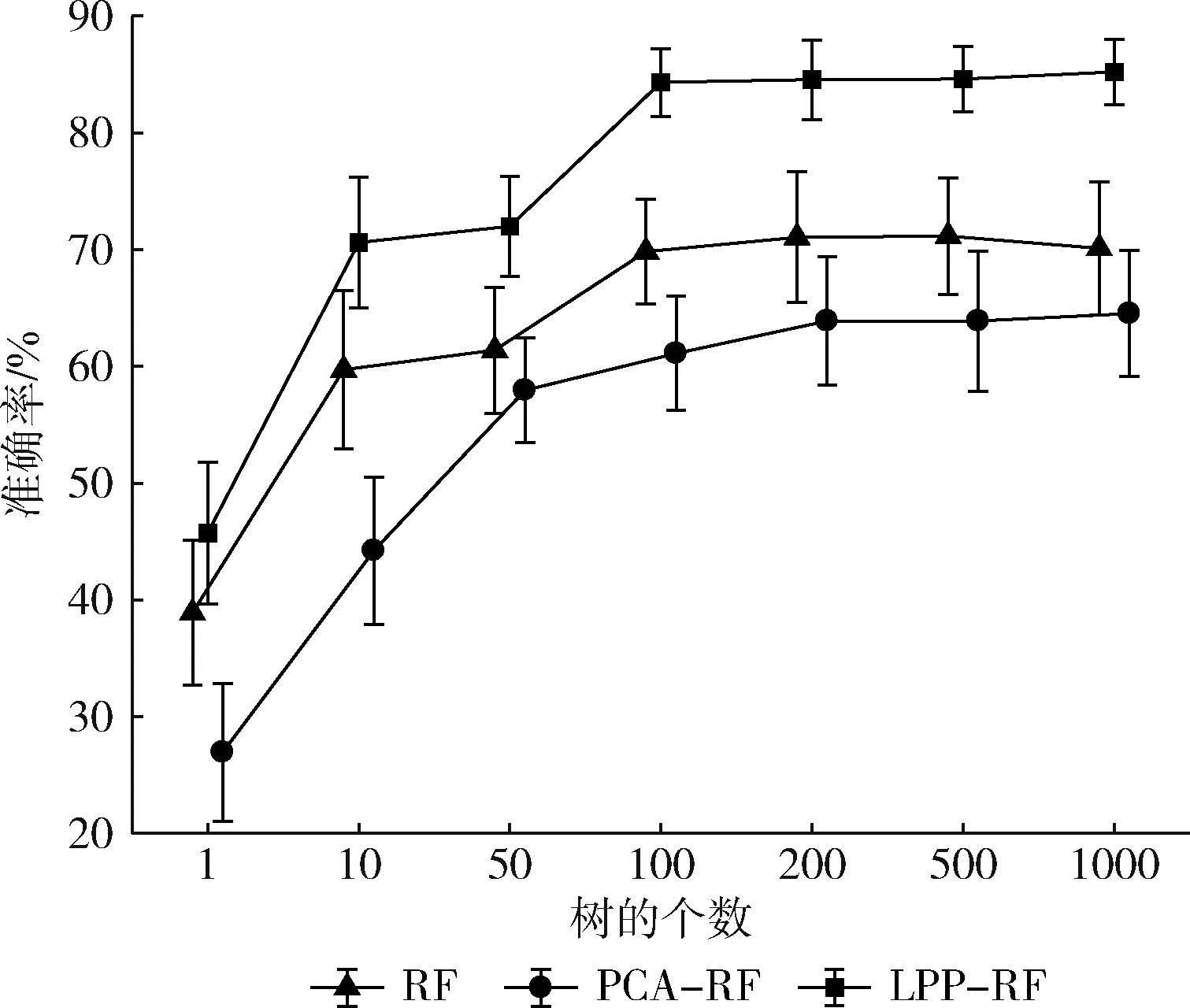
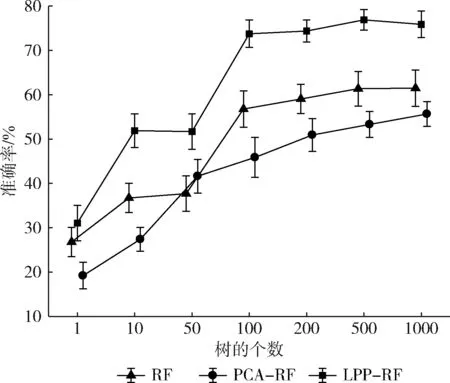
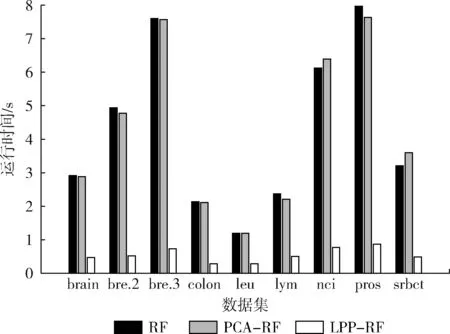
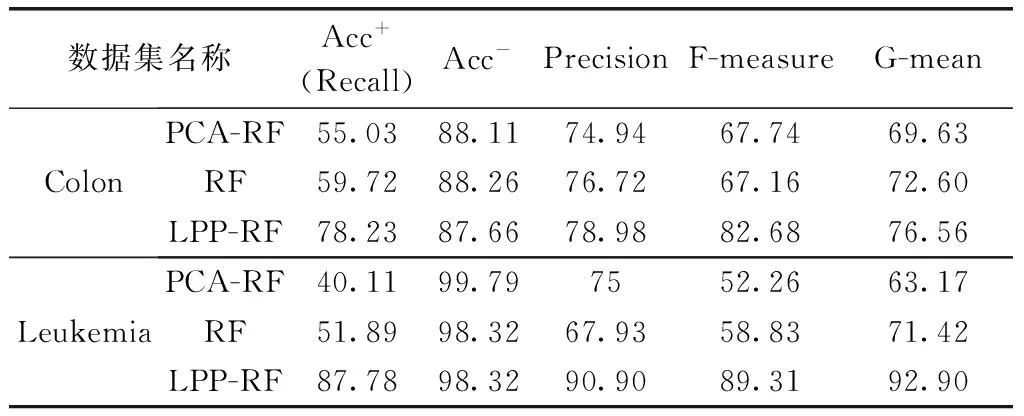
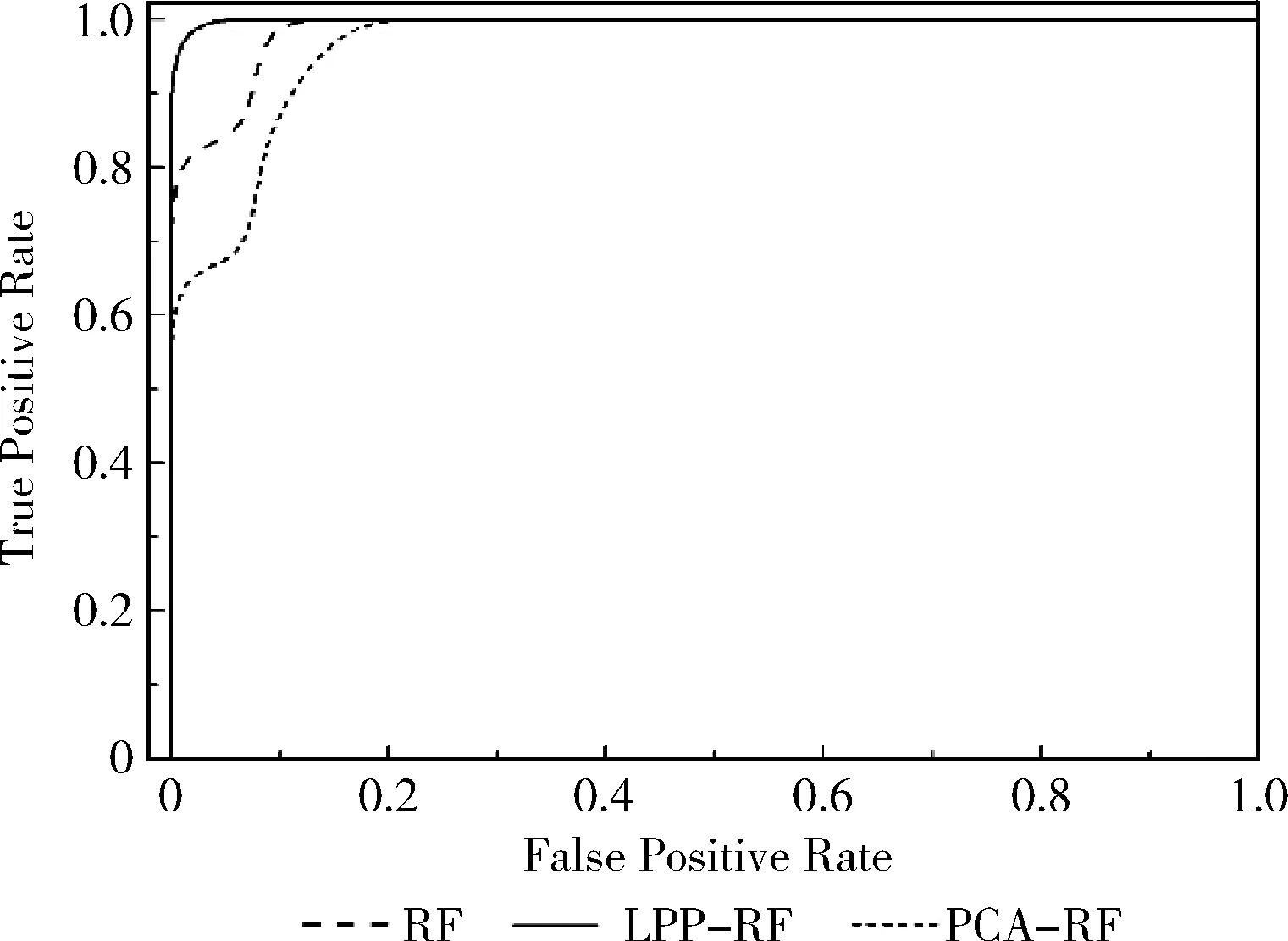
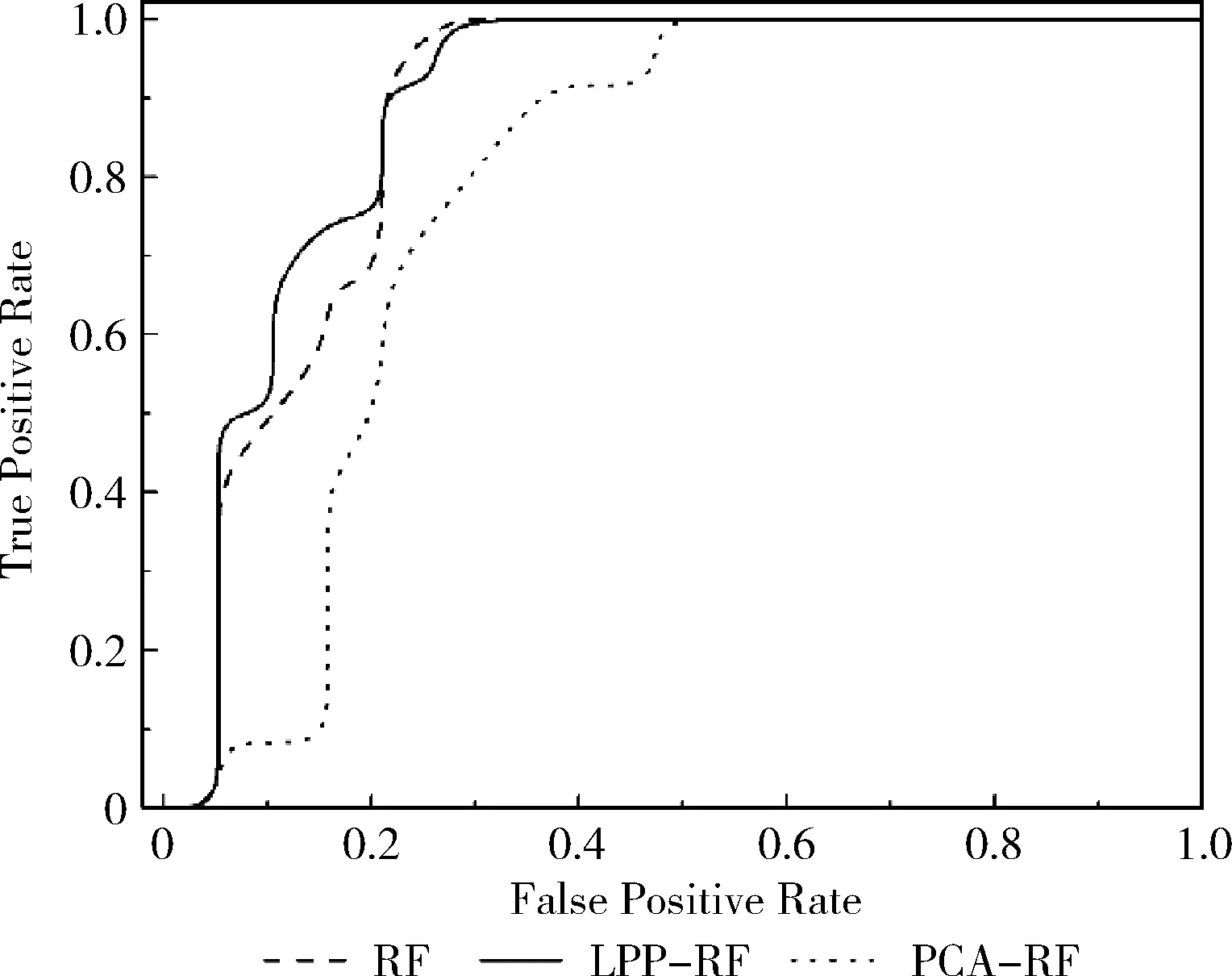
Bremain结合Bagging方法[8]和随机子空间划分[9]的策略,提出了RF算法。该算法是由多棵决策树组成的集成算法。在构造每棵决策树的过程中,先对样本集采用Bootstrap抽样方法,从样本总量为N的数据集中抽取N个样本,每次抽样均采取有放回的随机抽样方法,并将这N个样本作为该决策树训练时的样本集。在决策树的每个节点分裂过程中,RF算法随机选取mtry个属性(0 通过随机重采样和随机属性选取,使得RF算法具有以下几个特点[5,10-12]:①不易出现过拟合问题;②并行化程度高;③对噪声和异常点容忍度高;④适用于高维小样本数据;⑤适用于二分类和多分类任务。基因表达数据具有样本小、维数高、噪声多等特点。这些优点使得RF算法在基因表达数据分类上表现突出。 对于基因表达数据这样的高维非线性数据,通常要先采取非线性降维方法对数据进行预处理。常用的非线性降维方法是基于核的方法[13]和非线性流形学习的方法[14]。但前者需要人们凭经验选取核函数,找到合适参数需要花费较高的人工成本,且对测试样本没有清晰的映射函数。后者虽能够保持原始数据的结构特征,但与基于核的方法一样没有提供对测试样本的清晰映射函数。He等提出了LPP算法[15],该算法近似于非线性拉普拉斯特征映射。作为线性算法,相比核的方法和非线性流形学习的方法,该算法善于发现高维非线性数据中已有的低维流形结构,找到映射关系并提供清晰的映射函数。因此,LPP算法可以很好的应用于非线性数据降维问题中。 LPP原理是通过一定的性能目标去寻找变换矩阵A,以实现对高维数据的降维。变换矩阵A可以通过最小化以下目标函数得到[15] (1) 其中,xi和xj是样本集中的单个样本,W可通过如下式子进行定义 (2) 式中:t是一个控制相似性度量范围的常量,超出该范围的数据点之间的相似性逐级递减。对式(1)进行简单的代数变换,目标函数可以转化为 (3) D为对角矩阵,Dii=∑jWij,L=D-W是一个拉普拉斯矩阵。因此求解式(1)的最小化目标函数问题可以通过求解下式的广义特征向量得到 XLXTA=λXDXTA (4) 变换矩阵A由式(4)的l个最小非0特征值所对应的特征向量构成。 本文提出基于LPP的RF算法(random forest based on LPP,LPP-RF),将LPP算法应用在决策树的每个节点中,可以解决RF算法中决策树对于基因表达数据不能产生良好决策面的问题。 在决策树中每一次节点进行分裂之前,先通过变换矩阵A将该节点数据映射到新的属性空间中,实现对高维数据的降维。变换矩阵A也可以通过求解式(5)的广义特征向量得到[16] XWXTA=λXDXTA (5) 式(5)的l个最大非0特征值所对应的特征向量构成变换矩阵A=[a1,a2,…,al]。式(5)与式(4)不同的是将求解最小特征值问题转化为求解最大特征值问题,这样便于在新的映射空间中进行基尼指数计算。 由于在基因表达数据中,属性数量远大于样本数量,导致XDXT为奇异矩阵,此时无法对式(5)进行广义特征向量求解。经研究发现,将X进行奇异值分解[17],可以避免XDXT为奇异矩阵。X通过奇异值分解为 X=UEVT (6) 其中,将X的奇异值根据大小降序排列,构成对角矩阵E中对角线上的元素,U和V都是正交矩阵。 由于基因表达数据具有高维和噪声多双重特性,在进行奇异值分解以后将数据进行降维,设置阈值为β,删除E中与最大值比值小于β的奇异值和对应的奇异向量。 然后令B=EUTA,将式(6)带入式(5)得 XWXTA=λXDXTA⟹UEVTWVEUTA= (7) 其中,VTDV为非奇异矩阵,假设B为该式求得的特征向量矩阵,则 A=UE-1B (8) 求得变换矩阵A以后,对X进行映射构成新的数据集H H=ATX (9) 对式(8)进行求解以后,变换矩阵A中的特征向量是根据特征值大小降序排列,特征值可以表明该属性的重要性,在决策树算法中,节点的分裂是根据属性的重要性由大到小依次进行分裂的,因此在数据集H中只计算第一个属性的基尼指数,求出该属性的最佳分裂属性值并划分数据集H。然后根据数据集H的划分情况将数据集X进行同等划分,本次节点分裂完成。 算法1描述了LPP-RF算法中决策树的生成过程:首先判断数据集S是否为叶节点,如果是叶节点,则构建叶节点并返回类别标签(步骤(1));如果不是叶节点,则从数据集S中随机选择mtry个样本属性构成数据集Z(步骤(2));并将类别标签加入Z中以方便计算W的值(步骤(3));对于Z中相同类别标签的样本zm和zn,求出zm与zn之间的欧式距离(步骤(6))和wmn(步骤(7)),对于Z中不同类别标签的样本zm和zn,wmn等于0(步骤(9));得到权值矩阵W以后求出对角矩阵D(步骤(12));此时判断Z中属性个数和样本个数之间的大小,如果属性个数大于样本个数,需将Z进行奇异值分解(步骤(14)),在奇异值分解的过程中对Z进行降维(步骤(15)-(17));然后计算特征值与特征向量(步骤(18))及求出变换矩阵A(步骤(19));如果Z中的属性个数小于样本个数,可以直接计算求出A(步骤(23));构建属性空间Z1并计算最佳分裂属性值CFA(步骤(25)-(26));将计算得到的结果保存在当前节点中便于节点分裂及测试数据使用(步骤(27));根据最佳分裂属性值CFA对Z1进行分裂形成左右两个子节点,根据Z1的分裂结果将S进行同等划分(步骤(29));对S划分完的两个子节点进行递归构建,最后返回整棵决策树(步骤(30)-(32))。 算法1: Lpp_Rftree(S,mtry) 输入: 训练数据集S,节点抽取属性个数mtry 输出:单棵决策树tree (1) if is Node(S) return Tag(S) (2)Z= Choice (S(:,1:end-1)) (3)Z=[Z,S(end)] (4) for eachzm,zn∈ rowZ (5) if Tag(zm)==Tag(zn) (6)oc=sqrt(zn.*zn+zn.*zm-2*zm*zn) (7)Wmn=exp(-oc/(2*t^2)) (8) else (9)Wmn=0 (10) end if (11)end for (12)D=full(Culation_sum(W, 2)) (13) if lenght(Z,2)>lenght(Z,1) (14) [B,I,P]=Culation_SVD(Z(:,1:end-1)) (15)LI=find_max(I) (16)In=search(I/LI<1e-12) (17) Delete(B(In)),Delete(I(:,In)),Delete(P(In)) (18) [C,~]=Culation_eig(P′*W*V,P′*D*P); (19)A=BI-1C (20) else (21) [A,ag]=Culation_eig(S′*W*Z,Z*D*Z′); (22) [~,cl]=reorder(ag) (23)A=A(:,cl(1:l)) (24) end if (25)Z1=ATZ(:,1:end-1) (26) CFA=ChoiceBestAttribute(Z1(:,1)) (27) H=saveMessage(S,A,CFA) (28) for eachi∈branchCount(CFA) (29)Si=split(s,Z1,CFA,i) (30)tree.childi=Lpp_Rftree(Si,mtry) (31) end for (32) returntree 由于基因表达数据具有高维非线性特征,直接在原始属性空间中寻找节点最优分裂标准,需要对基因表达数据中每个属性中全部可能的最佳分裂属性值进行测试,然而基因表达数据具有上千维的属性,依次计算会产生较大的时间开销。在算法1中只需要测试第一个属性中可能的最佳分裂属性值,很大程度上缩短了构建决策树的时间。同时LPP算法使映射后的数据不仅保持了原有数据结构,而且还使得同类之间数据更紧凑,不同类之间数据更分散,使得决策树在分裂时能够产生良好的决策面,提高决策树的性能。 在LPP-RF算法中每一次的Bootstrap抽样之后,约有36%的样本数据不在抽样之后的样本集中,这些数据被称为袋外数据[18]。袋外数据可以用来估计LPP-RF算法的泛化误差,也可以用来测试单棵决策树的分类准确率。在本文中,采用后者,通过袋外数据测试单棵决策树的分类准确率,将分类准确率作为该决策树加权投票时的权值。使得在LPP-RF分类器预测时,对决策树性能差的分类结果赋予较低的权重,性能好的分类结果赋予较高的权重,以此来增加LPP-RF算法的分类准确率。同时也弥补了每次构建决策树之后有部分数据未被使用的不足。 算法2描述了LPP-RF算法训练阶段的构建过程:首先对训练样本集S进行有放回的随机抽样得到新数据集Si(步骤(2));将未被抽到的数据集作为袋外数据Bi(步骤(3));在Si上执行算法1进行决策树生成(步骤(4));并利用Bi测试该棵决策树的分类准确率得到权值vi(步骤(5));保存决策树模型以及权值vi(步骤(6));将步骤(2)-(6)重复k次,得到LPP-RF模型LPP_RFModel(步骤(8))。 算法2: lpp_RfTrain(S,k,mtry) 输入: 训练数据集S,决策树数量k,节点抽取属性个数mtry 输出:LLP-RF模型LPP_RFModel (1) for eachi∈k (2)Si=Bootstrap(S) (3)Bi=S-Si (4)treei=lppRf_treeTrain(Si,mtry) (5)vi= lppRf_predict(Bi,treei) (6) LPP_RFMode=saveTree(treei,Yi) (7) end for (8) return LPP_RFModel 由于决策树的每个节点数据在划分之前,先通过变换矩阵A进行映射,在映射以后的属性空间中寻找最佳分裂属性。因此对于测试数据,每经过决策树的一个节点,需要将数据按照该节点分裂时使用的变换矩阵A进行变换。对于最终分类结果采用加权投票法求出,可以表示为 (10) 其中,H(x)为算法对测试数据的最终分类结果,vi表示第i棵决策树的权值,hi(x)表示第i棵决策树测试数据的分类结果,Y为类别标签,I(·)为示性函数。 RF算法性能主要取决于单棵决策树性能和各个决策树之间的差异性[12],单棵决策树性能越好或各个决策树之间差异性越大,则RF算法的分类准确率就越高。在LPP-RF算法中,决策树每个节点都是在不同属性空间中进行数据划分,提高了决策树之间的差异性以及单个决策树的分类准确率,同时也提高了决策树之间的差异性,最终达到提高原始RF算法分类准确率的效果。 LPP-RF算法在决策树中每个节点的分裂都需要计算D、W以及变换矩阵A,一定程度上增加了时间开销,但在计算最佳分裂属性值时,只需计算第一个属性的基尼指数便可求出,又大幅缩短了时间开销,最后通过实验分析得出LPP-RF算法的时间少于原始RF算法。 本节将通过9个公开的基因表达分类数据集来进行实验验证LPP-RF算法的性能,这些数据集被国内外学者大量引用,具有一定标准性。所选取数据集的情况见表1,数据来源于文献[19],其中含有5个多分类数据集和4个二分类数据集。 表1 基因表达数据集 为了验证LPP-RF算法分类准确率和运行时间的性能,实验将LPP-RF算法与RF算法以及Zhang文献中的PCA-RF[7]算法进行对比分析。实验采用15倍的10折交叉验证方法,将10折交叉验证运行15次,得到150个分类结果,将平均值作为各个算法的最终分类准确率,并计算其方差。实验硬件为 Intel 2.3 GHz和8.0 GB内存,所有算法用MATLAB实现。由于RF算法的并行化程度高,很容易并行实现,所以在算法中决策树的生成采用了4个并行池并行生成的策略进行实验。 在RF算法中,决策树每个节点抽取属性个数mtry的取值通常为log2p(p为样本总属性的个数)[6]。森林规模即决策树的数目分别取k={1,10,50,100,200,500,1000}。表2记录了9个数据集在不同的森林规模下,LPP-RF算法、PCA-RF算法和RF算法的分类准确率和方差。 图1和图2展示了在数据集Brain和Nci中分类结果的误差棒图,横坐标为不同决策树的个数,纵坐标为分类准确率,每个点上竖形线段的长短为方差。为了能够更清晰显示出方差大小,将图中RF算法折线向左平移了0.1个单位,PCA-RF算法折线向右平移了0.1个单位。 从表2中可以看出,当算法中决策树的个数为1时,LPP-RF的分类准确率在绝大多数数据集上都高于另外两个算法,证明LPP-RF算法提高了单棵决策树的分类精度。随着决策树个数的增多,这3个算法的分类准确率都有提高,但LPP-RF算法的分类准确率稳定高于另外两个算法。在分类准确率的方差上,随着森林规模的增加,LPP-RF的方差在绝大多数数据集上都低于PCA-RF、RF算法,所以,LPP-RF算法具有较好的稳定性。从图1和图2中可以看出,RF、PCA-RF和LPP-RF算法的准确率随着森林规模的增加而增加,并在森林规模为100时趋于稳定。 图3显示了当树的规模为100时这3种算法所消耗的时间情况。 由图3可以看出,LPP-RF算法的运行时间远低于另外 表2 不同森林规模下10个数据集上3个算法分类准确率及方差 图1 Brain数据集分类结果误差 图2 Nci数据集分类结果误差 图3 3种算法在各数据集运行时间对比 两个算法。通过对比可以发现LPP-RF算法比另外两个算法最多缩短了7倍的运行时间。 基因表达数据往往还有类不平衡的特性,针对类不平衡的数据集,往往单靠一个分类准确率不能准确的反映出一个分类器的好坏,例如,在癌症检测中,只有少数人患有癌症,正确识别出少数癌症患者是非常有意义的,传统分类算法经常将稀有类实例被误分为负类实例[20],这时候需要将召回率(recall)、真负率(Acc-)、几何平均数(G-mean)、精确率(precision)、召回率(recall)和F度量(F-measure)当作性能评价指标。 在分类准确率对比实验中可以得出当森林规模为100时,各个算法的性能趋于稳定,因此本次实验中森林规模为k=100。在实验中选取了上述数据集中类不平衡度最大的两个数据集进行实验,分别为Colon和Leukemia。Colon数据集中一共有62个样本,其中正类样本(样本少的一类)含有22个样本,占整个数据集的35.4%,Leukemia数据集一共有38个样本,其中正类样本含有11个样本,占整个数据集的28.9%。通过15倍的10折交叉验证法进行实验。 表3记录了RF,PCA-RF,LPP-RF这3个算法在这两个数据集下的Recall、Acc-、Precision、F-measure和G-mean的值。 表3 Colon数据集和Leukemia数据集性能 由表3可以看出,LPP-RF算法在没有降低Acc-的情况下提升了基因表达数据集中Recall、Precision、F-mea-sure和G-mean的值,这说明了LPP算法对基因表达数据中正类样本准确率低的问题也有一定改善。 为更直观的对这两个算法进行比较,图4和图5绘制了受试者工作特征曲线(receiver operating characteristic curve,ROC)[21],ROC曲线是以真正率为纵坐标,假正率 图4 Leukemia数据集ROC 图5 Colon数据集ROC 为横坐标,通过设置一系列的阈值,可以得到多个不同的真正率与假正率的值,这些值都是ROC曲线上的点。ROC曲线与坐标轴所围成的面积越大,性能越好。 通过图4和图5可知,LPP-RF算法的ROC曲线与坐标轴所围成的面积大于RF和PCA-RF算法,说明LPP-RF算法的性能优于另外两种算法。 本文通过结合LPP与RF算法的优点,提出基于LPP的RF算法(LPP-RF),提高了RF算法在基因表达数据分类方面的性能。该算法对RF算法中每棵决策树的节点数据先进行LPP映射,然后在映射后的空间中以第一个属性作为最佳分裂属性,并根据分裂结果将原始空间中的数据进行同等划分,最后对测试样本使用加权投票法进行分类。与原始RF和PCA-RF算法相比,本文算法提高了基因表达数据的分类准确率及缩短了运行时间,并对基因表达数据中正类样本准确率低的问题也有一定改善。下一步的研究将针对不平衡数据集中正类样本准确率低的问题,对本文算法继续进行研究与改进,进一步提高正类样本的分类准确率。 [1]Liu JX,Xu Y,Zheng CH,et al.RPCA-based tumor classification using gene expression data[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics,2015,12(4):964-970. [2]Das SR,Das K,Mishra D,et al.An Empirical comparison study on kernel based support vector machine for classification of gene expression data set[J].Procedia Engineering,2012,38(5):1340-1345. [3]LU Huijuan.A study of tumor classification algorithms using gene expression data[D].Xuzhou:China University of Mi-ning and Technology,2012:1-111(in Chinese).[陆慧娟.基于基因表达数据的肿瘤分类算法研究[D].徐州:中国矿业大学,2012:1-111.] [4]LU Huijuan,AN Chunlin,MA Xiaoping,et al.Disagreement measure based ensemble of extreme learning machine for gene expression data classification[J].Chinese Journal of Compu-ters,2013,36(2):341-348(in Chinese).[陆慧娟,安春霖,马小平,等.基于输出不一致测度的极限学习机集成的基因表达数据分类[J].计算机学报,2013,36(2):341-348.] [5]Chen X,Ishwaran H.Random forests for genomic data analysis[J].Genomics,2012,99(6):323-329. [6]Wickramarachchi DC,Robertson BL,Reale M,et al.HHCART:An oblique decision tree[J].Computational Statistics & Data Analysis,2016,96(C):12-23. [7]Zhang L,Suganthan PN.Random forests with ensemble of feature spaces[J].Pattern Recognition,2014,47(10):3429-3437. [8]Galar M,Fernandez A,Barrenechea E,et al.A review on ensembles for the class imbalance problem:Bagging,boosting,and hybrid-based approaches[J].IEEE Transactions on Systems,Man,and Cybernetics,Part C(Applications and Reviews),2012,42(4):463-484. [9]YAO Xu,WANG Xiaodan,ZHANG Yuxi,et al.A self-ada-ption ensemble algorithm based on random subspace and AdaBoost[J].Chinese Journal of Electronic,2013,41(4):810-814(in Chinese).[姚旭,王晓丹,张玉玺,等.基于随机子空间和AdaBoost的自适应集成方法[J].电子学报,2013,41(4):810-814.] [10]Ali J,Khan R,Ahmad N,et al.Random forests and decision trees[J].International Journal of Computer Science Issues,2012,9(5):272-278. [11]Qi Y.Random forest for bioinformatics[M].Ensemble machine learning.Springer US,2012:307-323. [12]XIE Jianbin.Visual machine learning 20[M].Beijing:Tsin-ghua University Press,2015:1-239(in Chinese).[谢剑斌.视觉机器学习20讲[M].北京:清华大学出版社有限公司,2015:1-239.] [13]Zhu X,Huang Z,Shen HT,et al.Dimensionality reduction by mixed kernel canonical correlation analysis[J].Pattern Recognition,2012,45(8):3003-3016. [14]Qiao H,Zhang P,Wang D,et al.An explicit nonlinear mapping for manifold learning[J].IEEE Transactions on Cybernetics,2013,43(1):51-63. [15]Xiaogang D,Xuemin T.Sparse kernel locality preserving projection and its application in nonlinear process fault detection[J].Chinese Journal of Chemical Engineering,2013,21(2):163-170. [16]Cai D,Chen X.Large scale spectral clustering via landmark-based sparse representation[J].IEEE Transactions on Cybernetics,2015,45(8):1669-1680. [17]Makbol NM,Khoo BE.Robust blind image watermarking scheme based on redundant discrete wavelet transform and singular value decomposition[J].AEU-International Journal of Electronics and Communications,2013,67(2):102-112. [18]Boulesteix AL,Janitza S,Kruppa J,et al.Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics[J].Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery,2012,2(6):493-507. [19]Deng H,Runger G.Gene selection with guided regularized random forest[J].Pattern Recognition,2013,46(12):3483-3489. [20]GUO Huaping,DONG Yadong,MAO Haitao,et al.Logistic discrimination based rare-class classification method[J].Journal of Chinese Computer Systems,2016,37(1):140-145(in Chinese).[郭华平,董亚东,毛海涛,等.一种基于逻辑判别式的稀有类分类方法[J].小型微型计算机系统,2016,37(1):140-145.] [21]Hajian-Tilaki K.Receiver operating characteristic (ROC) curve analysis for medical diagnostic test evaluation[J].Caspian Journal of Internal Medicine,2013,4(2):627-635.1.2 LPP算法
2 LPP-RF算法
2.1 决策树最佳分裂属性选取
λUEVTDVEUTA⟹UEVTWVB=
λUEVTDVB⟹VTWVB=λVTDVB2.2 LPP-RF算法描述
3 实验与分析
4 结束语
