基于FGM(1,1)的航段油耗预测模型

陈静杰，车 洁

(中国民航大学 电子信息与自动化学院，天津 300300)

0 引 言

除航空器本身能效和飞行员操纵行为之外，航空器运行环境中诸多因素对飞行油耗均有显著影响。主要因素包括：地速、空速、加速度、飞行高度、大气总温、风速、风向、倾斜角以及总重等，并且各因素的影响力在一次具体飞行过程中的各个飞行阶段均不相同。然而，对于固定机型航段油耗，空速、地速以及加速度等因素的影响不再具有明显的效应。

目前，基于QAR(quick access recorder)数据的油耗预测模型主要有两类，文献[1]中均有详细介绍。为了探究不完整数据集中的有价值信息，灰色预测理论得到了广泛应用，文献[2]对其应用进行了详细叙述。然而，传统的灰色预测模型GM(1,1)对于波动数据不能很好处理，背景值假定是一次累加生成序列的紧邻均值生成序列[3-5]。因此，适用于各种冲击扰动数据的缓冲算子[6-10]被相继提出，背景值的改进[2,3]也应用于各类灰色预测模型中。然而，并没有一种综合缓冲算子和背景值改进的灰色模型被提出，并且应用于实际问题中。

基于Xinjun Wang提出的T-FGM(1,1)模型[4]，参考其对first-entry GM(1,1)模型的改进，本文提出了一种基于单调函数弱化缓冲算子的综合灰色预测模型。结合真实的QAR数据，在给定外界条件下，基于QAR数据的缺失处理，预测、分析飞机航段油耗，在此基础上进行碳排放的核查和控制。

1 基于总重和巡航高度的固定机型航段油耗面板数据构造

油耗的各个影响因素交叉影响飞机燃油的消耗。因而,单纯考虑某一因素的影响力需要固定其它因素。考虑到我国受季风性气候的影响，本文采用同一飞行季度、固定机型、航段的300个航班QAR数据(根据文献[11]满足航段油耗区间估计最小样本量)，构造基于总重(在固定机型条件下反映了业载情况)和巡航高度的航段油耗面板数据，在弱化风速、风向以及大气总温对油耗的影响的情况下，分析航段油耗受业载和巡航高度的影响。航段油耗数据格式见表1。

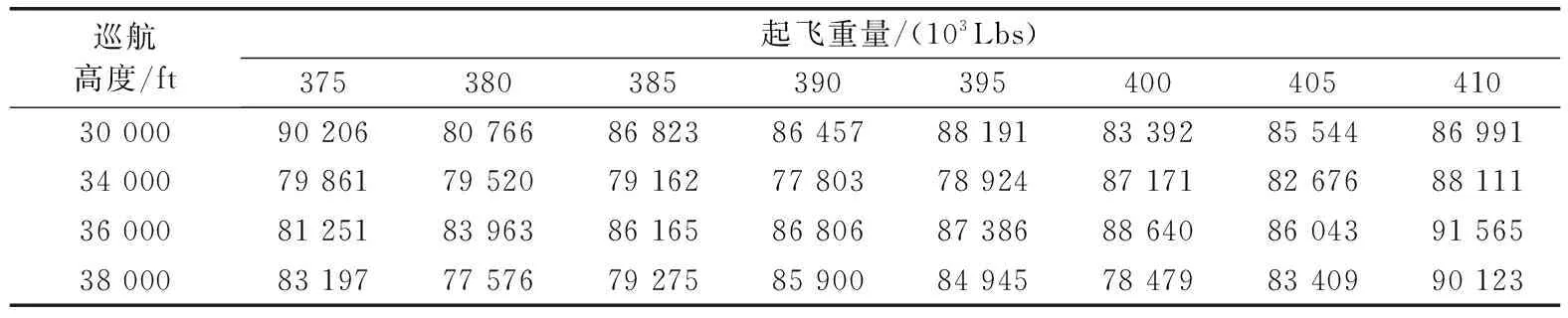
表1 第二季度上海-北京航段油耗数据

表1中，起飞重量采用以表1所示重量为中心，(-2.5,2.5)103Lbs为长度的重量区间。区间内航段油耗通过区间内各油耗以及对应的起飞重量信息熵权重加权平均得到。计算过程如下所示：

(1)单位化起飞重量

(1)

其中，n为区间内的数据个数，GW为飞机总重。

(2)计算第i个数据的熵值hi

hi=-(lnn)-1*pi*lnpi

(2)

(3)计算第i个数据的变异程度系数vi

vi=1-hi

(3)

(4)计算第i个数据的加权系数wi

(4)

(5)航段油耗FF

(5)

其中，FFi为第i个数据的飞机油耗。

通过表1中给出的数据，给定巡航高度下的总重和油耗关系如图1所示。从图1中可以看出，油耗与业载和巡航高度并不呈线性关系，根据图1的油耗分布情况，可以采用相同业载下油耗最少的巡航高度进行飞行，达到节油的目的。

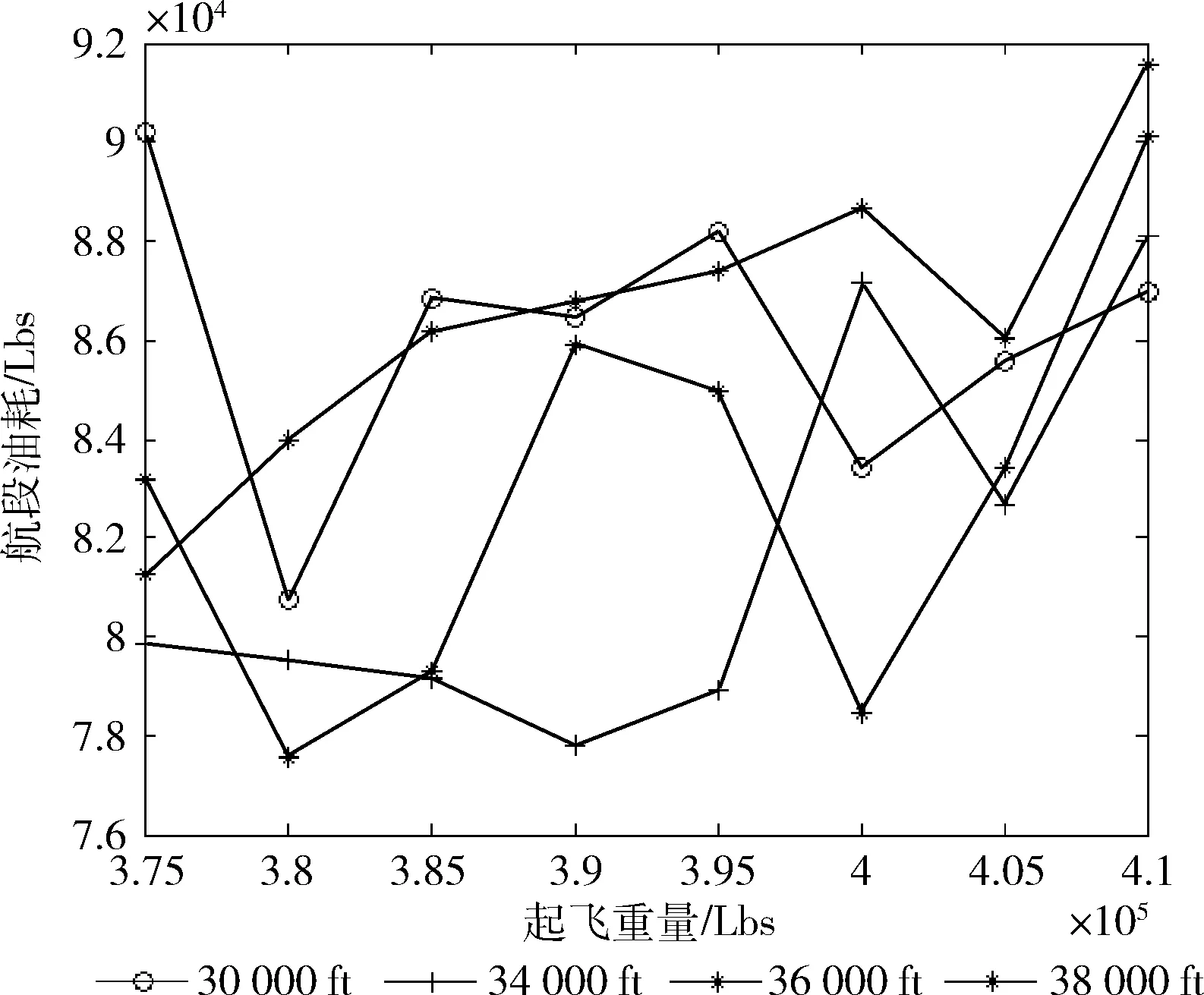
图1 不同巡航高度下的航段油耗

2 燃油流量数据缺失的影响和处理

由于QAR记录变量运行环境的复杂多变，以及后期数据存储和传输的不当都会使得几乎每一个航班的QAR数据出现不同参量不同程度不同类型的缺失，这将导致构造的面板数据不准确，影响后期的统计分析和决策制定。

为了对比分析缺失率小于15%时，燃油流量数据缺失对燃油的统计分析和预测带来的影响，根据文献[12]中对缺失数据类型的定义，人为构造表1中巡航高度为30 000ft时，385(103Lbs)重量区间内的1个航班QAR数据燃油流量小间隔随机缺失，缺失率为8.7%，数据缺失样本见表2(NULL表示数据缺失)。

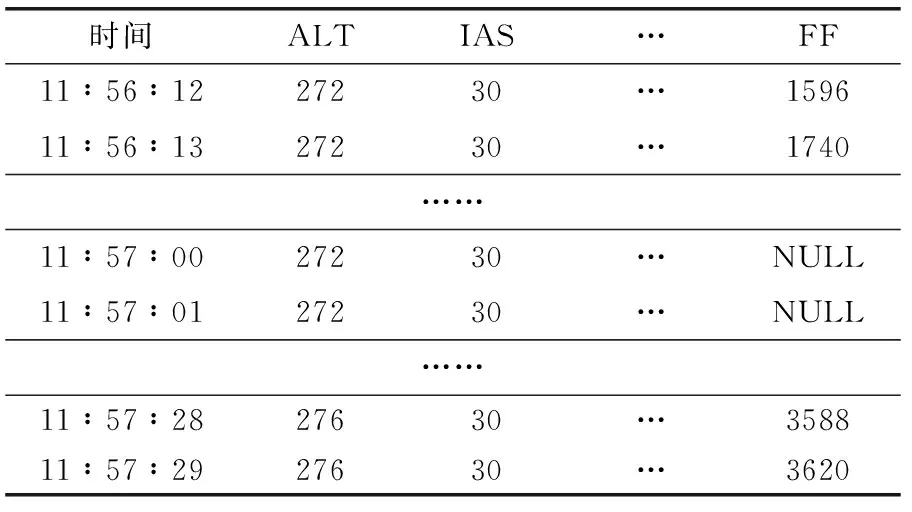
表2 缺失数据样本

此时，起飞重量为385(103Lbs)时，不同巡航高度的油耗数据见表3。从表3中可以看出，当缺失率为8.7%时，1个航班QAR数据的缺失即可导致整个油耗数据分布规律的变化，如果这些缺失数据不能合理地处理将导致决策的失误。因此，基于文献[12]提出的近邻规则缺失值填补算法，本文采用基于标准欧氏距离的K近邻填充算法对缺失的燃油流量数据进行估计。

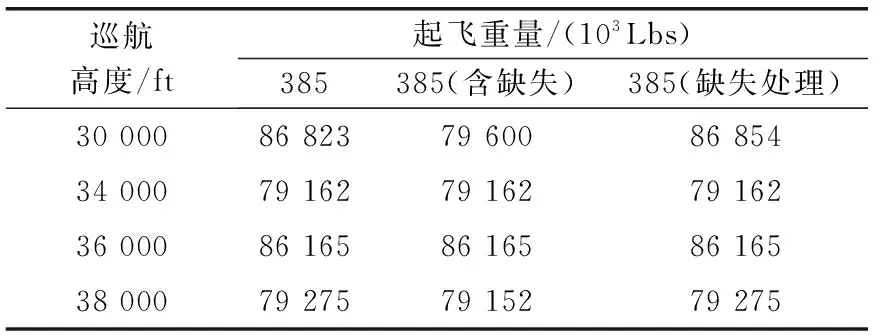
表3 考虑数据缺失的航段油耗

K近邻填充算法主要是通过分析缺失样本和已观测样本中影响燃油的相关因素参量之间的相似程度选择K个近邻样本。相似程度利用标准欧氏距离进行衡量，计算公式如下所示

(6)

其中，缺失样本记作：g=[g1,g2,…,gm]，完全样本为：zi=[zi1,zi2,…,zim]，m为样本维度，V为一次完整飞行过程中不含缺失值的完全数据样本的标准差。

通过对标准欧氏距离di信息熵的分析，根据第1节中使用的信息熵赋权法，得到K个近邻的权重。利用K个近邻油耗的加权平均得到估计油耗。缺失数据处理后的不同巡航高度的油耗数据见表3。从表3中可以看出，缺失值处理后航段油耗接近原始值，并且满足原来的油耗分布特征。

3 考虑数据缺失的航段油耗灰色预测模型设计

3.1 FGM(1,1)模型

First-entryGM(1,1)模型—FGM模型，由Tzu-LiTien提出[4]。他指出原始数据序列的第一个数据不影响发展灰数和灰色作用量的计算结果，除了作为初始值的使用，不参与整个预测过程，这将导致预测结果的失真。为了使所有数据参与运算，他提出了FGM模型，在原始数据序列之前添加一个任意值。具体步骤如下所示：

(1)初始化：令非负系统行为数据序列为X=(x(0),x(1),x(2),…,x(n))其中，x(0)为任意值。

(2)一阶累加生成序列X(1)

(7)

(3)背景值计算z(1)(r)

z(1)(r)=0.5(x(1)(r)+x(1)(r-1))

(8)

其中，r=1,2,…,n。

(4)发展灰数(a)和灰色作用量(b)的计算

[a,b]T=(BTB)-1BTYn

(9)

其中，Yn=[x(1),x(2),…,x(n)]T

(5)求解白化方程的时间响应函数序列:

白化方程为

(10)

时间响应函数序列为

(11)

还原后的模拟预测值为

(12)

3.2 基于单调函数弱化缓冲算子的综合灰色预测模型设计

基于FGM(1,1)模型[4]，考虑到油耗数据的波动性，结合弱化缓冲算子[6-10]对航段油耗数据进行波动调节，并采用自动寻优定权的方式[3]进行灰色预测背景值的确定，提出了一种基于单调函数弱化缓冲算子的综合灰色预测模型，具体步骤如下所示：

(1)原始序列波动调节—缓冲算子序列生成：根据弱化缓冲算子[8]，令f(x)=x2，生成缓冲算子序列XD，XD=(x(0),x(1)d4,…,x(n)d4),为了使原始数据的第一个数据参与预测过程，在缓冲算子序列前添加一个任意值x(0)。其中

(13)

式中：g为f(x)的反函数，wk为权重，采用第1节中采用的信息熵赋权法计算得到。

(2)一阶累加生成序列X(1),根据式(7)，形成新的累加生成公式

(14)

(3)背景值计算z(1)(r)：利用自动寻优定权方式[3]设定背景值z(1)(r)的计算公式，通过多次实验模拟，选择使模型精度最高的μ。背景值计算公式如下所示

z(1)(r)=μx(1)(r)+(1-μ)x(1)(r-1)

(15)

(4)求解白化方程的时间响应函数序列：根据式(10)所示白化方程的时间响应序列

由于发展灰数a的计算采用最小二乘法得到，这样会引入一定的误差。为了减小预测模型误差，利用偏差调节发展灰数，令a=a+ε，通过多次实验模拟选择使得模型精度最高的ε。白化方程的时间响应序列如下所示

(16)

(5)还原后的缓冲算子模拟预测值为

(17)

(6)模拟预测值为

(18)

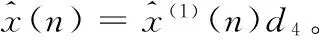
4 预测结果分析

实验利用A330飞机上海-北京航段真实QAR数据构造的基于总重和巡航高度的面板数据，验证本文提出模型的可行性和有效性。通过对模型的训练，当μ=0.65，ε=0.000 05时，模型的预测精度最高。

模型精度采用残差检验法[3]，残差序列记为E

(19)

相对误差记为ξ

(20)

均方根误差(rootmeansquarederror，RMSerror)为

(21)

灰色预测模型的精度为P

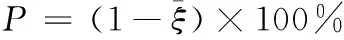
(22)

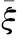
利用式(12)和式(18)，以及第2节提出的基于标准欧氏距离的缺失值填充算法，通过MATLAB仿真，分析巡航高度30 000 ft考虑数据缺失情况的航段油耗，预测效果见表4(表中斜体且带下划线的部分为含有缺失的数据)。从表4中可以看出，尽管灰色预测模型能够从不确定数据中提取出有用信息，抑制数据不确定性带来的影响。但是，经过缺失处理后的数据预测精度更高，更接近原始数据序列，肯定了缺失数据处理的必要性。

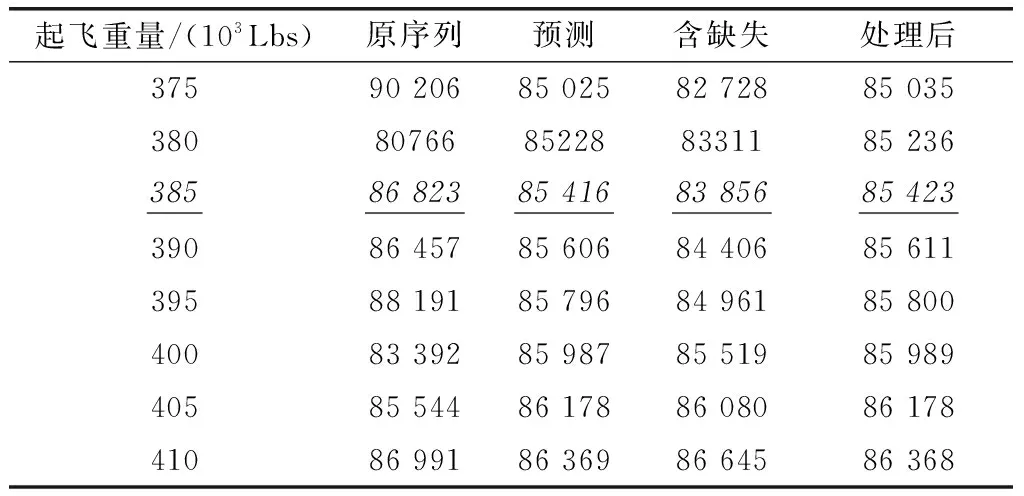
表4 巡航高度30 000 ft考虑缺失的航段油耗预测

根据式(21)和式(22)，对比分析FGM模型以及com_FGM模型的预测效果。为了验证背景值和发展灰数改进的必要性，在传统的FGM模型中引入与提出模型相同的弱化缓冲算子，记为New_FGM模型。并令com_FGM中ε=0，记为Ncom_FGM，用于验证发展灰数改进对预测精度的影响。不同灰色模型的模型预测精度见表5。对比表5中各列发现，引入弱化缓冲算子可以改进灰色模型的效果，但是效果不明显，背景值的改进显著提升了模型的精度和均方误差，但是对于波动较大的数据序列，预测效果不稳定。从表5中可以看出，对于不同的巡航高度燃油消耗，综合灰色模型都具有较高的预测精度，并且保持了较低的均方根误差，验证了模型的有效性。

表5 不同灰色预测模型的预测精度

5 结束语

本文参考目前提出的各类缓冲算子，结合现有的灰色预测模型及其改进模型，并考虑QAR数据的缺失问题，提出了一种航段油耗综合灰色预测模型。主要利用缓冲算子和偏差调节改进FGM(1,1)模型，并将其应用到基于标准欧氏距离的K近邻填充算法处理后的不同业载航段油耗预测中。实验结果表明，改进后的FGM(1,1)模型的预测精度更高，能够很好模拟给定巡航高度下业载和飞机消耗的关系，并且能够预测业载增加时的燃油消耗情况。这为航空公司进行燃油消耗的预测和监控提供了有力保障，也为碳排放的核查和控制提供了可靠的数据基础。该方法在对缺失数据处理的基础上而提出，避免了由于数据缺失而造成的统计失误。

[1]CHEN Jingjie,LI Meng.Fuel consumption prediction based on Bootstrap method under small size of samples[J].Measurement & Control Technology,2015,34(10):26-30(in Chinese).[陈静杰,李猛.小样本下基于Bootstrap的航程油耗预测方法[J].测控技术,2015,34(10):26-30.]

[2]LU Yi.The research and application of grey forecast model[D].Hangzhou:Zhejiang Sci-Tech University,2014(in Chinese).[卢懿.灰色预测模型的研究及其应用[D].杭州:浙江理工大学,2014.]

[3]YANG Hualong,LIU Jinxia,ZHEN Bin.Improvement and application of grey prediction GM(1,1) model[J].Mathematics In Practice and Theory,2011,41(23):39-46(in Chinese).[杨华龙,刘金霞,郑斌.灰色预测GM(1，1)模型的改进及应用[J].数学的实践与认识,2011,41(23):39-46.]

[4]Xinjun Wang.A novel T-FGM(1,1) forecasting model based on RBF neural network for water demand forecasting[J].Bio Technology,2013,8(4):551-554.

[5]Wu Lifeng,Liu Sifeng,Fang Zhigeng,et al.Properties of the GM(1,1) with fractional order accumulation[J].Applied Mathematics and Computation,2015,252(1):287-293.

[6]WANG Zhengxin,DANG Yaoguo,LIU Sifeng.A sort of power weaken buffer operators and its properties[J].Control and Decision,2012,27(10):1482-1488(in Chinese).[王正新,党耀国,刘思峰.一类幂弱化缓冲算子机器性质研究[J].控制与决策,2012,27(10):1482-1488.]

[7]ZHOU Weijie,DANG Yaoguo,LIU Hongsheng.Comparison of operator strength and smoothen between common weakening buffer and their multi-order operators[J].Systems Engineering-Theory & Pratice,2013,33(11):2903-2909(in Chinese).[周伟杰,党耀国,刘红生.弱化缓冲算子作用强度及光滑性比较[J].系统工程理论与实践,2013,33(11):2903-2909.]

[8]SU Yong.Study on the grey buffer operators and smoothness of buffer sequence[D].Hangzhou:Zhejiang Sci-Tech University,2013(in Chinese).[苏永.灰色缓冲算子与序列光滑性研究[D].杭州:浙江理工大学,2013.]

[9]YE Jing,LI Bingjun,LIU Fang.Forecasting effect and applicability of weakening buffer operators on GM(1,1)[J].Systems Engineering-Theory & Pratice,2014,34(9):2364-2371(in Chinese).[叶璟,李炳军,刘芳.弱化缓冲算子对GM(1,1)模型的预测效应及适用性[J].系统工程理论与实践,2014,34(9):2364-2371.]

[10]XU Ning,DANG Yaoguo.Construction of buffer operator with smooth variable weight and property[J].Control and Decision,2014,29(7):1262-1267(in Chinese).[徐宁,党耀国.平滑变权缓冲算子构造及其性质[J].控制与决策,2014,29(7):1262-1267.]

[11]CHEN Jingjie,XIAO Guanping.Minimum sample size analysis of aircraft segment fuel consumption interval estimation[J].Computer Engineering and Design,2014,35(12):4356-4360(in Chinese).[陈静杰,肖冠平.飞机航段油耗区间估计最小样本量分析[J].计算机工程与设计,2014,35(12):4356-4360.]

[12]WANG Fengmei,HU Lixia.A missing data imputation method based on neighbor rules[J].Computer Engineering,2012,38(21):53-55(in Chinese).[王凤梅,胡丽霞.一种基于近邻规则的缺失数据填补方法[J].计算机工程,2012,38(21):53-55.]

[13]YE Weiqiang,LIN Honggui.Application of grey theory to the prediction of diesel consumption of diesel generator set[C]//IEEE International Conference on Grey Systems and Intelligent Services,2013.