基于最小生成树的MCI脑网络分类

苗丽雯，田 程，李 婷，李佩珍，王 彬，曹 锐

(太原理工大学 计算机科学与技术学院，山西 太原 030024)

0 引 言

阿尔茨海默病(Alzheimer’s disease，AD)是导致痴呆的最主要原因之一[1]，轻度认知障碍(mild cognitive impairment，MCI)则是AD的早期表现。MCI和AD患者的脑网络研究中均发现不同程度的全脑或区域的功能连通性发生改变[2,3]。通过脑网络对MCI的分类研究提高MCI患者的诊断准确率，能够对痴呆的早期诊治起到较大的应用价值。

通常，脑网络分析首先计算时间序列两两之间的关联强度，构造加权连接矩阵。随后选择恰当的阈值或阈值范围，将加权矩阵转化成二值矩阵，即无权脑网络。然后计算各稀疏度下相应无权脑网络的拓扑属性，并对其属性值进行分析。该方法已经在很多研究中广泛使用并且取得了较大的成就，但其网络规模较大，计算过程中的时间代价和空间代价都非常大，同时在比较不同组和不同条件下各网络之间差异的过程中传统网络属性极易受到阈值选取以及网络平均连接强度的影响[4]。

最小生成树(minimum spanning tree，MST)是具有最小总权重的网络核心部分，连接了网络中的所有结点同时不构成环路。相同规模的网络产生的最小生成树具有相同的结点和连接数，这不仅避免了传统网络中存在的问题，也将网络规模减小到最小，大大节省计算的时间和空间[5,6]。之前儿童发育、癫痫、多发性硬化症、老化症和帕金森综合症的研究都证明MST是一个准确又敏感的研究方法[7-11]。据我们所知，目前还没有基于MST的MCI分类研究。

本文主要分析了MCI和正常对照组(normal control，NC)在无权网络和最小生成树中的拓扑属性差异，使用支持向量机(support vector machine，SVM)算法，将组间差异统计显著的拓扑属性作为特征，对3组被试进行两两分类研究，为MCI的分类研究提供新的思路。

1 数 据

本研究所用的静息态fMRI数据包括31例早期轻度认知障碍被试(early MCI，EMCI)，31例晚期轻度认知障碍被试(late MCI，LMCI)以及29例正常对照被试。所有图像数据均选自阿尔茨海默病神经影像计划(Alzheimer’s di-sease neuroimaging initiative，ADNI)数据库(http://adni.loni.ucla.edu/)。数据采集使用飞利浦(3T)MR扫描仪，设置slice thickness=3.3 mm；echo time (TE)=30 ms repetition time (TR)=3000 ms；48 slices。

被试基本信息，见表1。

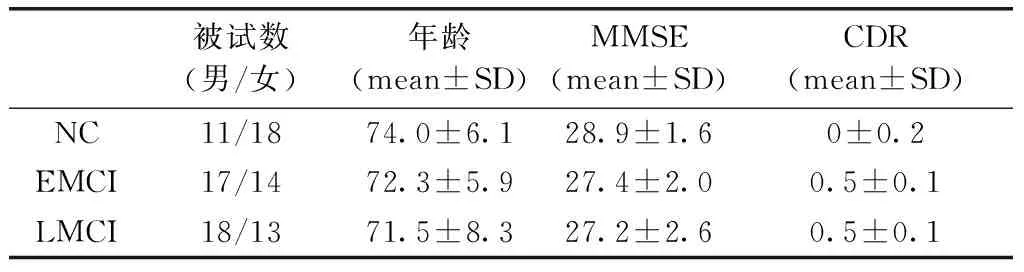
表1 被试基本信息

注：MMSE=Mini-Mental State Examination，简明精神量表。CDR=Clinical Dementia rating，临床老年痴呆量表。

实验主要使用DPARSF(data processing assistant for resting-state fMRI)对图像进行预处理。首先去除每个被试的前10个时间点，然后去除水平头动大于1 mm或者转动大于1°的被试。使用SPM提供的DARTEL(diffeomorphic anatomical registration using exponentiated lie algebra)将剩余图像标准化到3 mm体素的MNI(Montreal neurological institute)标准空间，并进行4 mm全宽半高(full width at half maximum，FWHM)高斯平滑，低频滤波频率设置为0.01 Hz-0.1 Hz，以降低低频漂移以及生物噪音。

2 相关矩阵构建

对预处理后的每个图像数据，使用自动化解剖学标签(anatomical automatic labeling，AAL)[12]提取时间序列得到一个M×N的矩阵(M为时间点数，N为脑区数)。AAL模版对全脑进行区域级大尺度结点划分，将全脑全部体素划分为90个感兴趣的区域(region of interest，ROI)作为脑网络结点节点，左右半脑各45个。然后计算每个ROI内的所有体素的平均时间序列作为该ROI的时间序列，计算每对ROI时间序列之间的皮尔森相关系数，作为结点之间的连接强度值，得到一个90×90的相关矩阵。皮尔森相关系数是反映两个向量之间线性关系的强度和方向的统计度量，计算得到的结点之间相关系数值越大表示结点之间的功能连接越强，本研究中将所有自相关和负相关值设置为零。

3 特征提取

3.1 无权网络特征提取

构建无权脑网络时，需要选取适当的阈值空间(稀疏度范围)将关联矩阵转换为一系列相应的只包含0和1的二值矩阵，然后计算各稀疏度对应的脑网络的拓扑属性。利用脑网络小世界属性特征，阈值的选取应使网络的平均度值大于2lnN(N=90)，同时网络的小世界标量σ>1.1，所以我们选择9%-40%为阈值空间，步长为1%，构造所有稀疏度下的无权脑网络，并计算在每个稀疏度对应的脑网络中结点的度，中间中心度(betweenness centrality，BC)和效率(结点度、中间中心度、全局效率、局部效率定义介绍请参见文献[13])以及每个属性值在各稀疏度空间内的曲线下面积(area under the curve，AUC)。

3.2 最小生成树特征提取

最小生成树是具有最小总权重的加权无向子图，包含了网络中所有的结点但不构成环路[14]。如果网络中所有的边权重是唯一的，生成的最小生成树也是唯一的[15]。最小生成树在鲁棒性方面不同于传统网络，它提供非常保守的估计[11]，虽然在MST构建期间丢弃了很多冗余连接，但是MST仍然能够敏感地度量出网络拓扑的变化[5]。

我们取相关矩阵中相关系数的倒数作为结点对之间的距离，使用Kruskal’s[16]算法计算每个相关矩阵的最小生成树。先构造一个具有90个结点的子图，把子图中每一个点都当成是一棵树的根结点，然后对网络中的边按距离值按升序排序，选择距离值最小的边，如果该边的两个顶点不属于同一棵树，则将其加入子图，把两棵树合成一棵树，已有连接不形成环路，反之，如果该边的两个顶点属于同一棵树，子图加入该边会形成环路，则跳过这条边，取下一条距离值最小的边重复之前的步骤。依次类推，直到森林中只有一棵树，即子图中含有89条边为止。我们取结点度的最大值，结点BC的最大值以及结点离心率的均值和树的叶子数、直径和树层次作为全局属性对MST的整体进行度量，结点属性上主要分析MST的结点度，BC和离心率(MST属性定义请参见文献[4,5])。

4 分类算法

本文使用SVM分类算法以及3种被试的无权网络属性和最小生成树属性进行分类研究。SVM算法是Vapnik教授根据统计学习理论提出的[17]，主要基于结构化风险最小化原则，将输入的样本数据借助核函数映射到高维空间，构建分类超平面寻找最优分类面进行分类，具有较高的泛化能力，能有效避免维数灾难，是当前比较主流的机器学习方法。

对于给定样本集Χ:{(xi,yi),i=1,2,…,n}，其中xi∈Rm,yi∈{-1,1}。根据结构风险最小化原则，构建训练集目标函数

(1)

其中，ξ是松弛变量，用来惩罚不能被准确分开的样本点；C为惩罚参数，表示对分类错误的惩罚程度；Ф(xi)是线性映射方程，实现样本数据从低维空间到高维空间的映射。求解得到最优分类超平面

g(x)=ωΤX+b=0

(2)

使分类误差达到最小。

在实验过程中对分类结果使用留一法交叉验证评价分类性能，即每次从待分类样本中选择一个样本作为测试样本集，其余为训练样本集，对样本进行分类得到一组分类灵敏度，特异度和正确率。如此对每个样本重复一次，取所有分类结果的均值来评价分类性能。

5 结 果

我们选择具有显著差异的结点属性值作为待分类样本特征，使用SVM分类算法对EMCI和NC，LMCI和NC以及EMCI和LMCI这3对被试组进行分类研究，采用留一法交叉验证估算分类的灵敏度、特异度、正确率和AUC。

5.1 无权网络特征选择和分类结果

我们使用单因素方差分析法对LMCI，EMCI和NC这3组被试的每个结点属性AUC值进行统计分析，结点属性的显著差异(p<0.05)在额叶区(左侧中央前回，脑岛以及左右眶内额上回)，顶叶区(左侧中央后回，缘上回和右侧角回)，枕叶区(左右枕上回)以及颞叶区(右侧颞中回和颞下回)都有表现，特别是右侧框内额上回在每个属性上都表现出非常明显的差异，表明这些脑区的大脑活动变化在痴呆病变的过程中表现出了非常重要的作用[18,19]。

我们在无权网上选择了8个差异显著(p<0.01)的结点属性值(全局效率：右侧框内额上回和颞中回；局部效率：枕上回；度：左侧中央前回、右侧框内额上回、脑岛、角回和颞中回)作为样本特征，采用SVM算法留一法交叉验证对EMCI和NC，LMCI和NC以及EMCI和LMCI进行分类。分类性能在表2中给出，ROC曲线如图1所示，EMCI和NC的分类效果较好，正确率为70%，AUC为0.82。

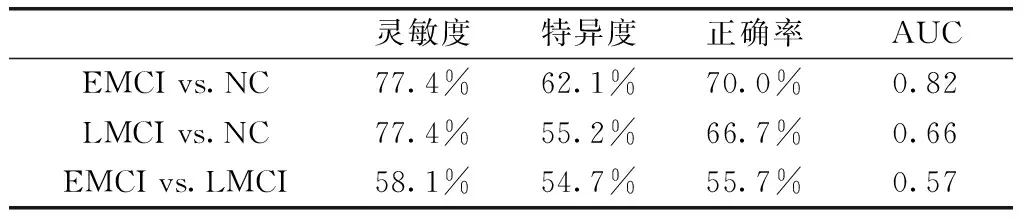
表2 无权网络特征在LMCI，EMCI和NC上的分类性能

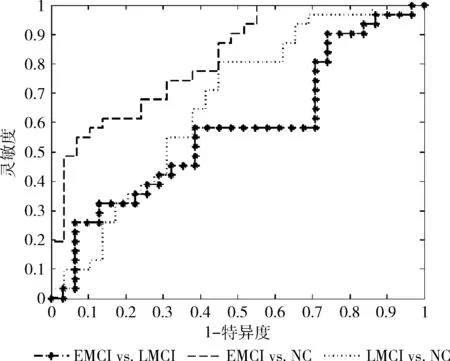
图1 无权网络特征分类ROC曲线

5.2 MST特征选择和分类结果

我们使用单因素方差分析法对LMCI, EMCI和NC这3组间的全局属性和局部属性进行统计检验，发现3组间MST全局属性差异主要表现在最大BC(p=0.03，F2,88=3.51)和树层次(p=0.002，F2,88=6.7)上。结点属性上，组间差异(p<0.05)主要集中在额叶区(左侧岛盖部额下回、补充运动区和右侧中央沟)和扣带回(左侧前扣带回、右侧旁扣带回和双侧后扣带回)，在右侧楔叶、缘上回、丘脑和颞中回上也有表现。这些差异在无权网络属性上没有表现，但是很多之前的研究也认为这些脑区和AD有关[20,21]。

我们选择最大BC和树层次以及差异显著(p<0.01)的结点属性作为分类样本特征对EMCI和NC，LMCI和NC以及EMCI和LMCI进行分类。SVM算法留一法交叉验证得到分类性能在表3中给出，ROC曲线如图2所示，LMCI和NC以及EMCI和LMCI的分类正确率分别为73.3%和64.5%，AUC值为0.79和0.69，相比无权网络特征都有提高。

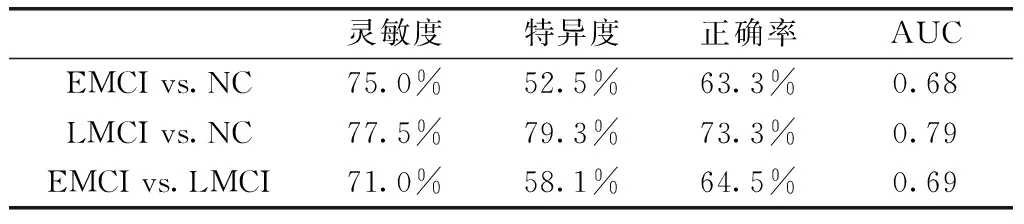
表3 MST特征在LMCI，EMCI和NC上的分类性能

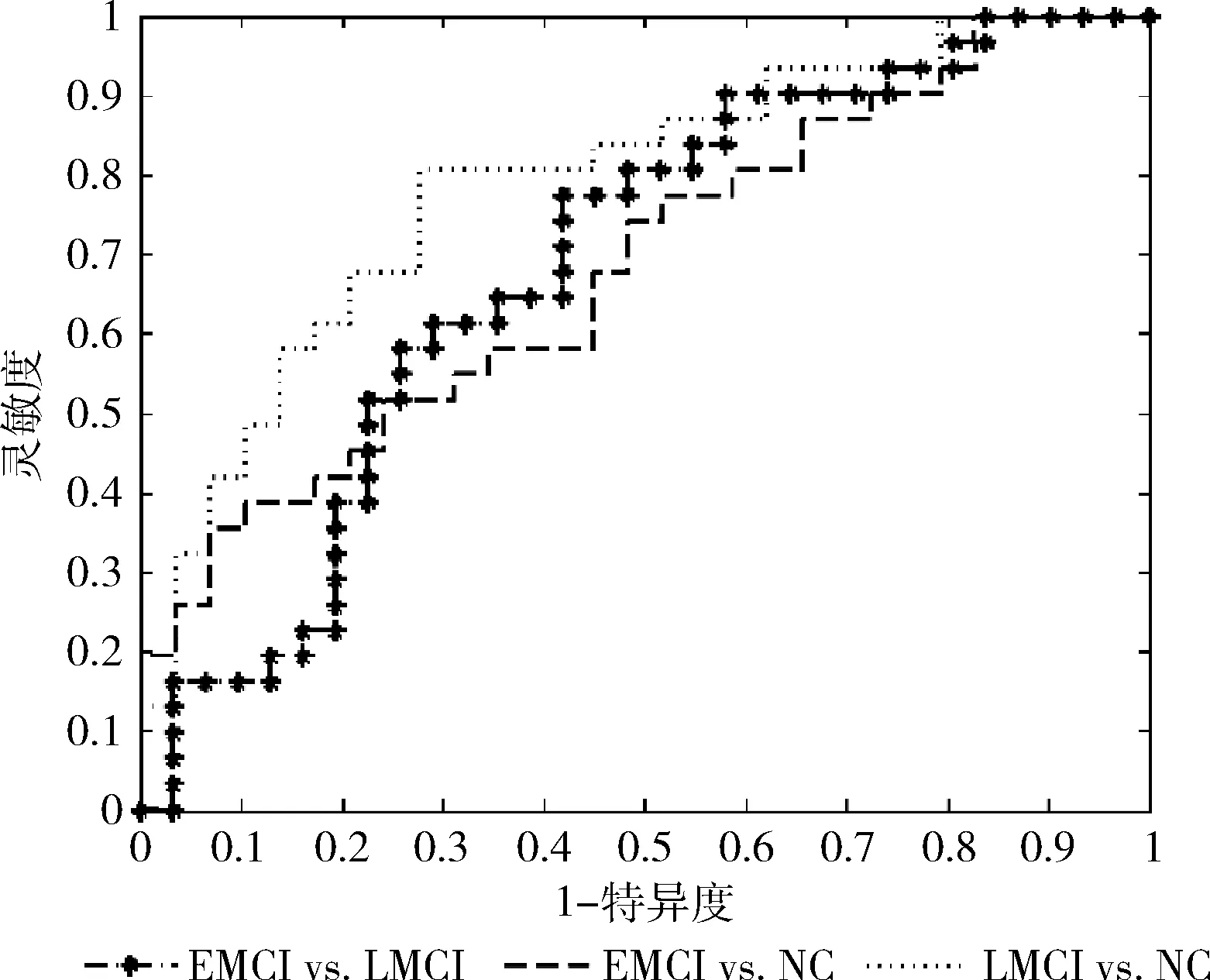
图2 MST特征分类ROC曲线

5.3 无权网络特征联合MST特征分类结果

将MST特征和无权网络特征一起作为样本特征放入SVM分类器，留一法交叉验证得到EMCI和NC，LMCI和NC以及EMCI和LMCI的分类性能见表4，ROC曲线如图3所示。分类性正确率比单独使用无权网络特征分别提高了10.3%，6.6%和16.9%，AUC值分别提高了0.05，0.16和0.15。

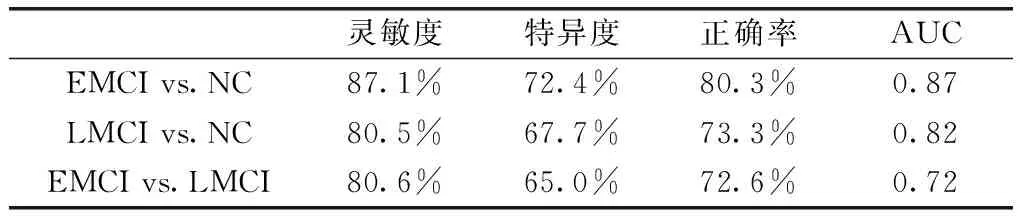
表4 MST特征和无权网络特征在LMCI，

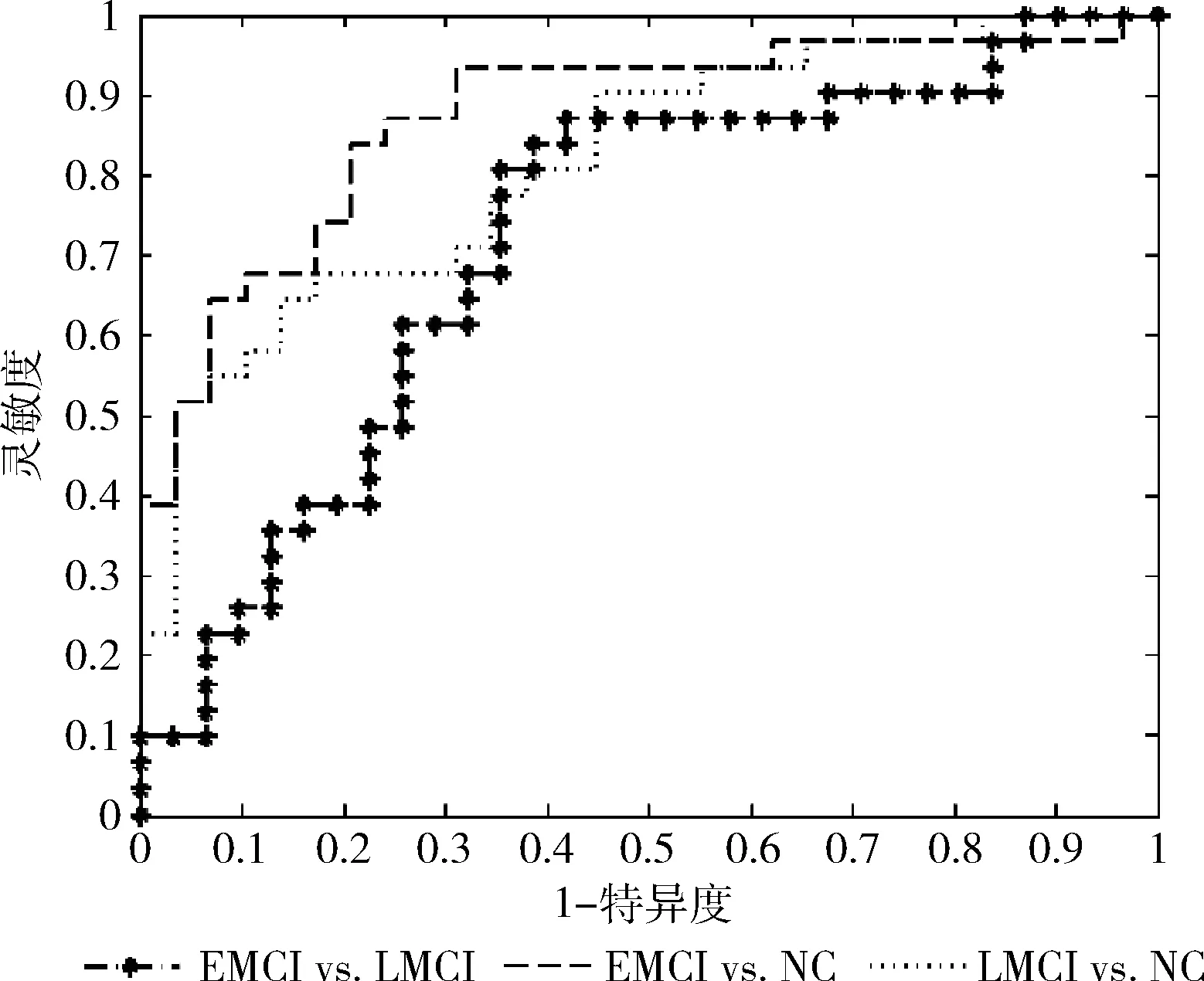
图3 MST特征和无权网络特征的分类ROC曲线

6 讨 论

最小生成树是一个数学定义的可以反映网络最基本属性的无偏差子网络，在缩小网络规模的同时保留了网络中最关键的部分[14,15]，同时MST网络属性与无权网络属性强烈相关[5]。众多研究结果也显示最小生成树是一个无偏差的网络分析方法，它不仅能准确地反映网络底层拓扑的细微变化，还可以避免功能连接和底层拓扑混合的方法偏差[8,9,11,22]，允许相同大小的网络之间的无偏差比较[4]。

我们在MST属性的研究中检测出了一些无权网络属性中不容易发觉的网络拓扑差异，例如扣带回(在前扣带回，旁扣带回和后扣带回上都有表现)和丘脑处的结点属性差异，Scheff等[20]和Dai等[21]也证明这些区域的差异与AD相关。利用这些差异对NC，EMCI和LMCI进行分类后，发现MST特征在LMCI与NC和EMCI与LMCI上分类得到的分类正确率和AUC值相对无权网络特征都有提高。近几年也有一些使用图论方法对MCI和NC的分类研究。接标等[23]在图核的基础上使用SVM分类方法对NC和MCI以及EMCI和LMCI进行分类研究，得到的分类正确率分别为82.6%和67.7%。Ali等[24]提取AD，MCI和NC在AAL模版上的有向网络特征，使用SVM分类方法进行分类得到3组间的分类正确率为71.95%。MST仅保留网络关键部分，对网络底层拓扑的变化非常敏感，我们单独使用MST特征在LMCI与NC上的分类正确率可以达到73.3%，证明MST属性可以用于AD早期检测。

武政等[25]提取了网络属性以及结构像中的灰质体积作为分类特征，训练SVM分类器，对AD，MCI和NC进行多模态分类研究，网络属性对AD和NC，MCI和NC以及AD和MCI的分类正确率分别为70.6%，78.3%和71.4%。基于多模态的思想，我们将无权网络和MST两类特征结合后对LMCI，EMCI和NC进行分类，得到的正确率和AUC值与之前相比都有非常显著的提高。最小生成树网络规模小，运算速度快，能准确地刻画脑网络之间的差异，分类过程中可以将MST特征作为无权网络特征的补充，二者结合后进一步提高分类性能。在后续的工作中我们将对分类算法做出改进，以求更好的分类性能。

7 结束语

本文主要使用传统无权网络和最小生成树对LMEI，EMCI和NC之间的结点属性进行分析比较，然后借助SVM分类算法，将无权网络和最小生成树拓扑属性作为样本特征，对EMCI、LMCI和NC这3组样本进行两两分类研究。我们的研究结果证明最小生成树可以检测到网络关键结构之间的差异，更准确度量脑网络的拓扑结构变化，从而提高网络分类的正确率，更好辅助AD的早期的诊断。

[1]Henderson VW.Alzheimer’s disease:Review of hormone therapy trials and implications for treatment and prevention after menopause[J].The Journal of Steroid Biochemistry and Molecular Biology,2014,142:99-106.

[2]Wang J,Zuo X,Dai Z,et al.Disrupted functional brain connectome in individuals at risk for Alzheimer’s disease[J].Biol Psychiatry,2013,73(5):472-481.

[3]Liang P,Li Z,Deshpande G,et al.Altered causal connectivity of resting state brain networks in amnesic MCI[J].PLoS One,2014,9(3):e88476.

[4]Stam CJ,Tewarie P,Van Dellen E,et al.The trees and the forest:Characterization of complex brain networks with minimum spanning trees[J].Int Journal Psychophysiol,2014,92(3):129-138.

[5]Tewarie P,Van Dellen E,Hillebrand A,et al.The minimum spanning tree: An unbiased method for brain network analysis[J].Neuroimage,2015,104:177-188.

[6]Sweeney SM,Middleton AA.Minimal spanning trees at the percolation threshold:A numerical calculation[J].Phys Rev E Stat Nonlin Soft Matter Phys,2013,88(3):032129.

[7]Olde Dubbelink KT,Hillebrand A,Stoffers D,et al.Disrupted brain network topology in Parkinson’s disease:A longitudinal magnetoencephalography study[J].Brain,2014,137(Pt 1):197-207.

[8]Tewarie P,Hillebrand A,Schoonheim MM,et al.Functional brain network analysis using minimum spanning trees in multiple sclerosis:An MEG source-space study[J].Neuroimage,2014,88(2):308-318.

[9]Van Dellen E,Douw L,Hillebrand A,et al.Epilepsy surgery outcome and functional network alterations in longitudinal MEG:A minimum spanning tree analysis[J].Neuroimage,2014,86(1):354-363.

[10]Boersma M,Smit DJ,Boomsma DI,et al.Growing trees in child brains:Graph theoretical analysis of electroencephalography-derived minimum spanning tree in 5- and 7-year-old children reflects brain maturation[J].Brain Connect,2013,3(1):50-60.

[11]Otte WM,Van Diessen E,Paul S,et al.Aging alterations in whole-brain networks during adulthood mapped with the minimum spanning tree indices:The interplay of density,connectivity cost and life-time trajectory[J].Neuroimage,2015,109:171-189.

[12]Qi S,Meesters S,Nicolay K,et al.The influence of construction methodology on structural brain network measures:A review[J].Journal Neurosci Methods,2015,253:170-182.

[13]Garrison K A,Scheinost D,Finn ES,et al.The (in)stabi-lity of functional brain network measures across thresholds[J].Neuroimage,2015,118:651-661.

[14]Yu M,Hillebrand A,Tewarie P,et al.Hierarchical clustering in minimum spanning trees[J].Chaos:An Interdisciplinary Journal of Nonlinear Science,2015,25(2):023107.

[15]Dorrigiv R,Fraser R,He M,et al.On minimum- and maximum-weight minimum spanning trees with neighborhoods[J].Theory of Computing Systems,2015,56(1):220-250.

[16]Lee YJ.An efficient implementation of kruskal’s algorithm for a minimum spanning tree[J].Journal of the Korea Society of Computer and Information,2014,19(7):131-140.

[17]Corinna Cortes VV.Support vector machines applications[M].New York:Springer,2014.

[18]Sacuiu S,Insel PS,Mueller S,et al.Chronic depressive symptomatology in mild cognitive impairment is associated with frontal atrophy rate which hastens conversion to alzheimer dementia[J].The American Journal of Geriatric Psychiatry,2016,24(2):126-135.

[19]Guo Z,Liu X,Hou H,et al.Abnormal degree centrality in Alzheimer’s disease patients with depression:A resting-state functional magnetic resonance imaging study[J].Exp Gerontol,2016,79:61-66.

[20]Scheff SW,Price DA,Ansari MA,et al.Synaptic change in the posterior cingulate gyrus in the progression of Alzheimer’s disease[J].J Alzheimers Dis,2015,43(3):1073-1090.

[21]Dai Z,Yan C,Li K,et al.Identifying and mapping connectivity patterns of brain network hubs in Alzheimer’s disease[J].Cereb Cortex,2015,25(10):3723-3742.

[22]Vourkas M,Karakonstantaki E,Simos PG,et al.Simple and difficult mathematics in children:A minimum spanning tree EEG network analysis[J].Neurosci Lett,2014,576:28-33.

[23]JIE Biao,ZHANG Daoqiang.The novel graph kernel for brain networks with application to MCI classification[J].Chinese Journal of Computers,2016,39(8):1667-1680(in Chinese).[接标,张道强.面向脑网络的新型图核及其在MCI分类上的应用[J].计算机学报,2016,39(8):1667-1680.]

[24]Khazaee, A, Ebrahimzadeh A, Babajani-Feremi A. Classification of patients with MCI and AD from healthy controls using directed graph measures of resting-state fMRI[J]. Behav Brain Res, 2016, 322: 339-350.

[25]WU Zheng,XIANG Jie,LIANG Hong,et al.The AD Classification model based on mutimodality MRI[J].Journal of Taiyuan University of Technology,2015,46(1):85-88(in Chinese).[武政,相洁,梁红,等.基于多模态MRI的AD分类模型[J].太原理工大学学报,2015,46(1):85-88.]