混沌元胞果蝇算法在云计算中的应用
2018-03-16曹国震王建军张少茹
战 非,曹国震,王建军,张少茹
(1.西安航空学院 计算机学院,陕西 西安 710077;2.西安交通大学 医学院护理系,陕西 西安 710049)
0 引 言
果蝇算法(fruit fly optimization,FOA)[1,2]应用在云计算中对海量数据进行处理,解决大型复杂问题时存在一定的缺点,包括初值的选择对算法求解精度存在影响、收敛速度慢、易陷入局部最优等[3]。近年来研究者们针对标准果蝇算法提出了相关的改进策略。如文献[4]中提出通过引入果蝇因子,自适应调整果蝇搜索步长,提高算法速度;文献[5]中引入免疫记忆特性,对果蝇算法的解进行优化,避免出现早熟现象;文献[6]中提出递减步长的果蝇算法进行优化;文献[7]中通过将迭代寻优过程分为果蝇移动范围逐步增大和逐步减小两个阶段,以提高种群多样性等。
上述研究者对果蝇算法的改进主要集中在优化迭代过程的中间解,没有过多考虑初始解群的优劣对算法的影响。本文提出一种引入混沌理论和结合元胞自动机的改进算法,通过结合混沌运动的优势,将优化变量通过Logistic映射规则映射至混沌变量空间内,利用混沌变量特点寻优搜索,再将得到的优化解线性转至优化空间,完成初始解群的优化。然后在算法迭代过程中,利用元胞自动机演化规律,进行最优种群的选择和替换。最后在云计算环境下通过实验验证了该算法在求解精度和收敛速度上更优。
1 果蝇算法
1.1 算法原理
果蝇算法基于自然界果蝇种群的觅食行为,果蝇个体通过嗅觉区分空气中的不同味道,同时通过视觉发现食物和身边果蝇同伴的位置,通过判断调整飞行的方向[8]。算法具体流程如下:
(1)初始化种群规模sizePop和算法最大迭代次数maxGen,随机生成果蝇群体初始位置X_axis和Y_axis;
(2)计算果蝇个体嗅觉寻找食物的随机方向和距离
(1)
其中,Xi和Yi表示下一位置的横坐标和纵坐标,Value代表搜索距离,rand()代表0到1的随机数;
(3)因无法确定食物位置,需估算果蝇个体与原点距离矢量Di,然后计算味道浓度判定矢量Si
(2)
(3)
(4)将Si代入味道浓度判定函数,即适应度函数,计算得出每个果蝇个体位置的适应度(即味道浓度)Smelli
Smelli=fit(Si)
(4)
(5)寻找出当前果蝇种群中最佳适应度Smellg和最佳位置坐标xg、yg;
(6)令Smellbest=Smellg,将当前种群最佳位置作为新一次算法迭代的初始位置,即X_axis=xg,Y_axis=yg,此时果蝇种群利用视觉飞向该位置;
(7)重复执行步骤(2)~步骤(5),判断最佳适应度是否优于上次迭代产生的最佳适应度,同时当前迭代次数是否小于最大迭代次数,若是则执行步骤(6)。
1.2 蝇算法的不足
判断算法的优劣,可以从收敛性、求解精度和执行效率等方面评判。收敛性是指随着算法的迭代执行,算法结果逐渐逼近真实结果进而趋近于一个稳定的值,趋近固定值的过程越快即收敛性越好。求解精度通俗来讲指算法进行最优值求解时,最优解的小数点后的位数,位数越高代表算法求解精度越高,算法也越优。执行效率指算法执行的时间,一般而言时间越短效率越高,算法也越优。
由于云计算中数据量巨大,处理问题较为复杂,同时云服务应用于互联网的特点又要求具有相对较高的执行效率和响应速度。基本果蝇算法应用在云计算中存在以下缺点:
(1)算法求解精度对初值的选择呈现出敏感性和不稳定性,初值选择较好能够获得较高的求解精度,初值选择不当可能引起求解精度降低。由于果蝇算法初值完全依赖随机选择,不具备有界性及遍历性,导致算法易出现不稳定性。
(2)果蝇算法迭代过程中,每次仅选择本次迭代得到的最优个体,所有果蝇飞向当前最优位置,但若当前最优非全局最优,则易出现收敛速度慢、易发散和陷入局部最优等现象,影响云计算效率。
2 元胞自动机
元胞自动机(cellularautomata,CA),代表一种时间和空间离散的动力系统,散布在规则网格中的个体元胞取有限的离散状态,遵循同样的作用规则,依据确定的局部规则进行更新同步。元胞个体周围根据相应规则划定的元胞集合称为邻居,当前元胞的下一时刻状态根据自身及其邻居状态确定[9]。
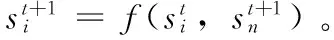

图1 元胞自动机邻居模型
元胞演化规则为:
(1)根据图1中扩展Moore邻居模型规定,选择阴影区域Mi(i=1,2,…)的中心元胞,计算所有区域的最佳味道浓度(即适应度)作为初始值,Vibest=min(f(si0),f(si0),…,f(si0)),其中si0为味道浓度判断值。
(2)对单个区域Mi,取其中的任意元胞Ci,计算Vi=f(s1),f(s2),…,f(si),若Vi 本文主要利用元胞自动机的演化规则,对果蝇算法每一轮迭代的解进行优化处理。 混沌是一种按照特定规律运动的非线性现象,在一定范围内可以实现无重复遍历。本文讨论的混沌主要指一种对初始条件较敏感的时间演化行为,具有有界性和遍历性的特征。有界性指通过混沌吸引子,混沌运动的轨迹始终规定于一个确定区域。遍历性是指在混沌运动的范围内能够遍历所有状态[10,11]。本文的研究和实验都基于Logistic映射,其迭代公式为 xi+1=μxi(1-xi),i=0,1,2…,0<μ≤4 (5) 其中,μ为控制参数,xi+1∈(0,1)。当3.569 945 6<μ≤4时,Logistic映射表现出混沌状态;当μ=4时,呈现典型混沌特征。 本文通过Logistic映射进行混沌优化策略如下: (1)产生随机混沌量。 对式(5)取取μ=4,并进行变换产生混沌变量Cxi,公式如下 Cx(n+1)i=4Cx(n)i(1-Cx(n)i),i=0,1,… (6) 其中,Cx(n)i指所产生的混沌变量Cxi在第n步混沌变换后的值。 (2)优化变量和混沌变量进行往返映射[12]。 Cxi=(xi-ai)/(bi-ai) (7) (8) 以上步骤就完成了将优化变量映射至混沌空间,然后可以利用混沌系统的有界性和遍历性进行优化,再将优化解转换回优化空间。 根据前文分析果蝇算法在云计算中的缺点,这里提出一种结合混沌理论和元胞自动机演化规则的改进算法—混沌元胞果蝇算法(CCF)。算法具体改进策略如下: (1)针对果蝇算法对初值的敏感性和不稳定性,引入混沌映射对初值进行优化。由于果蝇算法随机选择的初值不具备遍历性和有界性,对求解精度有较大的影响,这里利用混沌映射的遍历性和有界性,先将果蝇算法产生的初值即优化变量,通过Logistic映射到混沌空间,使其具有混沌特性,然后再转换回优化变量空间,完成对初值的优化。 (2)针对果蝇算法易陷入局部最优和收敛速度慢的缺点,引入元胞自动机的演化规则进行最优种群选择,根据演化所得适应度和当前最优适应度进行比较和替换,使果蝇种群跳出局部最优。 这里提出的混沌元胞自动机果蝇算法(CCF)的算法流程如下: (2)根据式(7)将Zi各分量映射为混沌变量Cz(n)i,Cz(n)i∈[0,1]; (3)根据式(6)对Cz(n)i的各分量进行混沌操作; (5)将果蝇个体适应度值放入F[m][n]二维数组中,依次按行放置,根据扩展Moore邻居模型取n=5,m=sizePop/5; (6)根据本文第2节中元胞自动机演化规则,选择果蝇优秀个体并保留最优个体位置,复制并替换之前的果蝇位置; (7)执行第1节中果蝇算法的步骤(2)~步骤(6),记录果蝇种群中最佳适应度Smellbest和最佳位置坐标xg、yg; (8)判断最佳适应度是否优于上次迭代产生的最佳适应度,同时当前迭代次数是否小于最大迭代次数,若是转至步骤(5)。 本次实验采首先采用Sphere函数、Ackley函数、Schwefel1.2函数和Zakharov函数对CCF算法的求解精度和收敛性进行测试,实验结果横向比较标准果蝇算法(FOA)。为了体现两种算法测试过程中的公平性,测试过程没有放入分布式计算环境中进行。该4种高维优化测试函数解得分布都比较复杂,函数存在较多的拐点和障碍,在进行最小值求解时易陷入局部最优。4种函数公式分别为: (1)Sphere函数如式(9)所示 (5)在数组O=[ot,r]4×r的第四行中,随机改变某子批量在工序间流转过程中的搬运设备,并按照FCFS规则生成搬运设备选择相邻解。 (9) (2)Ackley函数如式(10)所示 (10) (3)Schwefel1.2函数如式(11)所示 (11) (4)Zakharov函数如式(12)所示 (12) 4种函数的特征见表1。 表1 4种测试函数的特征 实验中设最大迭代次数maxGen=250,种群个数sizePop=50,算法单独执行30次,测试函数维数分别取10维、30维和50维。对比标准果蝇算法(FOA)结果见表2。 由表2中的数据分析可得,CCF算法通过引入混沌映射对算法初值进行优化,所得到解的精度要远高于FOA算法,平均值也比FOA算法更逼近测试函数的最优解。以Zakharov函数为例,FOA算法在求解精度较低时已经陷入局部最优且无法跳出,但是CCF算法却能够在更大范围内搜索,并获得较好的最优解。综合数据表明CCF算法能够较有效地跳出局部最优,优于FOA算法。 表2 测试函数实验结果 设4种测试函数维数为30,取CCF算法一次执行过程中迭代收敛曲线如图2~图5所示。 图2 Sphere函数迭代曲线 由图2~图5可以分析得出,CCF算法在经过混沌初值变换和每轮迭代过程中进行元胞自动机演化,有效提高了算法的收敛速度,执行效率要高于FOA算法。 通过CloudSim云仿真软件搭建实验环境,创建云计算节点和分发任务数,设定服务参数和创建虚拟机。模拟资源调度对CCF算法进行测试,根据服务要求搜索最优路径。仿真中使用特定函数的参数如带宽(bw),内存(ram),PE数(pesNumber)等的设置,根据目前常规虚拟机硬件水平设置[13-15],仿真流程如图6所示。 图3 Ackley函数迭代曲线 第一部分实验:取计算节点为20,任务数由20变化至100,CCF算法和FOA算法各执行20次,结果取平均值,同时计算任务分配结果的相对标准差。实验结果如图7和图8所示。 第二部分实验:由于受虚拟机条件制约,实验模拟的云环境从规模上要远小于实际中的云计算环境,为了表现云规模即计算节点数量对算法的影响,固定任务数为40,计算节点数为10变化至80,执行过程不变,在每个变化节点数上CCF和FOA算法各执行10次取平均值,执行时间如图9所示。 图4 Schwefel 1.2函数迭代曲线 图5 Zakharov函数迭代曲线 图6 CloudSim仿真流程 图7 任务执行时间对比 图8 相对标准差结果 图9 不同节点对应执行时间对比 由图7和图8分析可得,随着任务数的增加,CCF算法的执行时间要优于FOA算法,当任务数越多,CCF算法效率优势越明显,符合云计算的需要。同时CCF算法的偏差值随着任务数的增加也越来越小趋于线性渐进,也优于FOA算法。由图9分析可得,当计算节点数量增多,CCF改进算法在执行效率上越来越优于经典的果蝇算法。综上所得,本文提出的混沌元胞果蝇算法能够较好的克服果蝇算法的不足,更加适用于云计算。 本文在标准果蝇算法的基础上引入混沌理论和元胞自动机演化规则对其进行改进,提出了混沌元胞果蝇算法(CCF)。该算法利用混沌运动的特征对算法初值进行优化,然后在每一轮算法迭代中通过元胞自动机演化规则去优化果蝇种群,寻找最优适应度并进行替换。通过优化测试函数实验和云仿真实验,验证混沌元胞果蝇算法在求解精度、收敛性和执行效率上要优于果蝇算法,更适合应用在云计算中。本文算法只是用混沌映射进行初值的优化,若每轮迭代都引入混沌特征进行优化结果如何,还需要后期进一步的研究。 [1]PAN Wenchao.Fruit fly optimization[M].Taipei sea Book Company,2011:1-12(in Chinese).[潘文超.果蝇最佳化演算法[M].台北沧海书局,2011:1-12.] [2]XIAO Zheng’an.Design of analog filter based on fruit fly optimization algorithm[J].Journal of Hubei University of Education,2012,29(2):26-29(in Chinese).[肖正安.基于果蝇优化算法的模拟滤波器设计[J].湖北第二师范学院学报,2012,29(2):26-29.] [3]LIU Zhengwei,WEN Zhongling,ZHANG Haitao.Cloud computing and cloud data management technology[J].Journal of Computer Research and Development,2012,49(S1):26-31(in Chinese).[刘正伟,文中领,张海涛.云计算和云数据管理技术[J].计算机研究与发展,2012,49(S1):26-31.] [4]YANG Shuquan,SHU Qin,HE Chuan.A modified fruit fly algorithm and its application in PPI network[J].Computer Applications and Software,2014,31(12):292-294(in Chinese).[杨书佺,舒勤,何川.改进的果蝇算法及其在PPI网络中的应用[J].计算机应用与软件,2014,31(12):292-294.] [5]WANG Xin,DU Kang,QIN Bin,et al.Drying rate modeling on FOALSSVR[J].Control Engineering of China,2012,19(4):631-638(in Chinese).[王欣,杜康,秦斌,等.基于果蝇优化算法的LSSVR干燥速率建模[J].控制工程,2012,19(4):631-638.] [6]NING Jianping,WANG Bing,LI Hongru,et al.Research on and application of diminishing step fruit fly optimization algorithm[J].Journal of Shenzhen University Science and Engineering,2014,31(4):368-372(in Chinese).[宁剑平,王冰,李洪儒,等.递减步长果蝇优化算法及应用[J].深圳大学学报理工版,2014,31(4):368-372.] [7]XU Fuqiang,TAO Youtian,LYU Hongsheng.Improved fruit fly optimization algorithm[J].Journal of Soochow University(Natural Science Edition),2014,29(1):17-20(in Chinese).[徐富强,陶有田,吕洪升.一种改进的果蝇优化算法[J].苏州大学学报,2014,29(1):17-20.] [8]HAN Junying,LIU Chengzhong.Fruit fly optimization algorithm with adaptive mutation[J].Application Research of Computers,2013,30(9):2641-2644(in Chinese).[韩俊英,刘成忠.自适应变异的果蝇优化算法[J].计算机应用研究,2013,30(9):2641-2644.] [9]YAO Canzhong,YANG Jianmei.Cellular automata simulation of group behavior driven by dual-targets[J].Computer Engineering and Applications,2012,48(1):27-29(in Chinese).[姚灿中,杨建梅.双目标推动下群体行为的元胞自动机模拟[J].计算机工程与应用,2012,48(1):27-29.] [10]ZHAN Fei,ZHANG Shaoru.A research on application optimization of cloud computing based on chaos ant colony algorithm[J].Fire Control & Command Control,2017,42(7):25-28(in Chinese).[战非,张少茹.基于混沌蚁群算法的云计算应用优化研究[J].火力与指挥控制,2017,42(7):25-28.] [11]LI Wen,LIANG Ximing.A hybrid algorithm based on chaos optimization and steepest descent algorithm[J].Computing Technology and Automation,2003,22(2):12-14(in Chinese).[李文,梁昔明.基于混沌优化和最速下降法的一种混合算法[J].计算机技术与自动化,2003,22(2):12-14.] [12]MO Yuanbin,CHEN Dezhao,HU Shangxu.Chaos particle swarm optimization algorithm and its application in biochemical process dynamic optimization[J].Journal of Chemical Industry and Engineering(China),2006,57(9):2123-2127(in Chinese).[莫愿斌,陈德钊,胡上序.混沌粒子群算法及其在生化过程动态优化中的应用[J].化工学报,2006,57(9):2123-2127.] [13]ZHAN Fei,ZHANG Shaoru.Chaos harmony search algorithm base on scheduling of cloud computing[J].Computer Engineering and Design,2017,38(7):1823-1827(in Chinese).[战非,张少茹.基于混沌和声的云计算调度算法[J].计算机工程与设计,2017,38(7):1823-1827.] [14]ZHAN Fei,ZHANG Shaoru.A research on cloud computing scheduling based on chaos particle swarm optimization algorithm[J].Electronic Design Engineering,2017,25(5):13-17(in Chinese).[战非,张少茹.基于混沌粒子群算法的云计算调度研究[J].电子设计工程,2017,25(5):13-17.] [15]ZHAN Fei,ZHANG Shaoru.Research on applications of chaos cuckoo search algorithm suitable for cloud computing[J].Control Engineering of China,2017,24(7):1486-1492(in Chinese).[战非,张少茹.适应云计算的混沌布谷鸟算法应用优化研究[J].控制工程,2017,24(7):1486-1492.] [16]QIAN Fucai,FEI Chuhong,WANG Baiwu.A hybrid algorithm for finding global minimum[J].Information and Control,1998,27(3):232-235(in Chinese).[钱富才,费楚红,万百五.利用混沌搜索全局最优的一种混合算法[J].信息与控制,1998,27(3):232-235.] [17]Li J,Jia C,Li J,et al.Outsourcing encryption of attribute-based encryption with MapReduce[C]//Information and Communications Security-14th International Conference.Berlin:Springer Berlin Heidelberg,2012:191-201. [18]Hao M,Wlodarczyk TW,Rong C.Performance analysis and optimization of map only left outer join[C]//Proceedings of the 27th International Conference on Advanced Information Networking and Applications Workshops IEEE Computer So-ciety.New York:ACM,2013:625-631.3 Logistic混沌映射转换
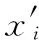
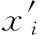
4 混沌元胞果蝇算法研究
4.1 算法改进策略
4.2 算法流程
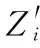
5 实验及分析
5.1 优化函数测试
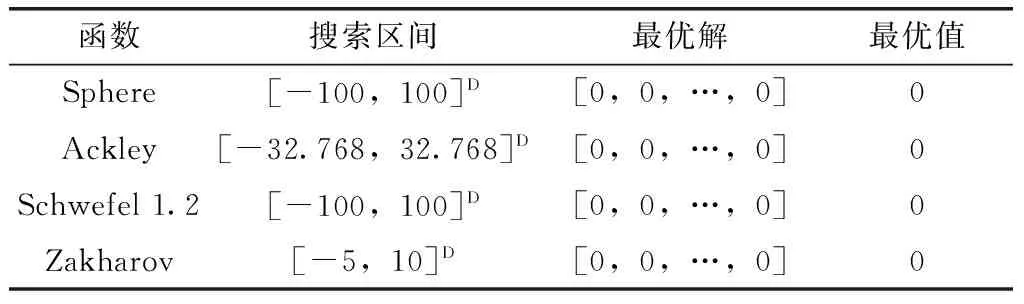
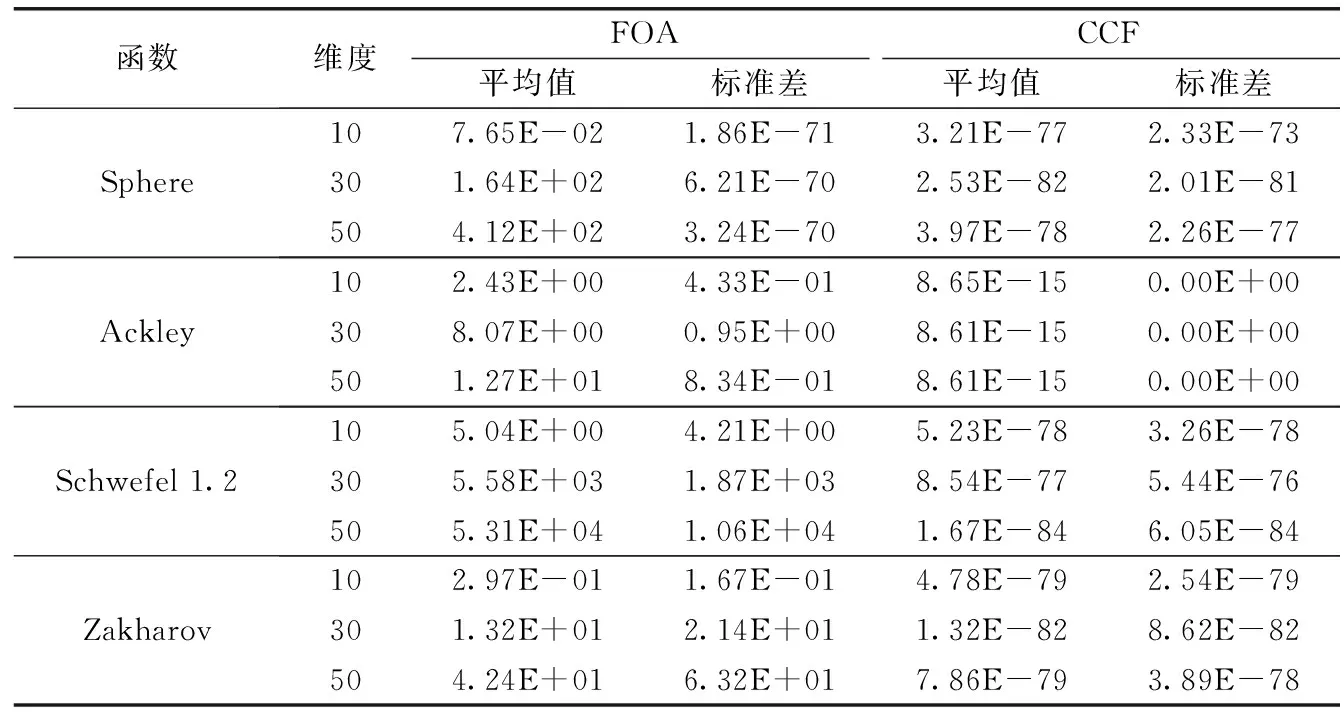
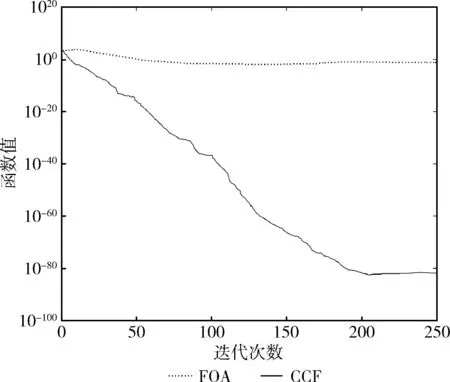
5.2 云仿真实验



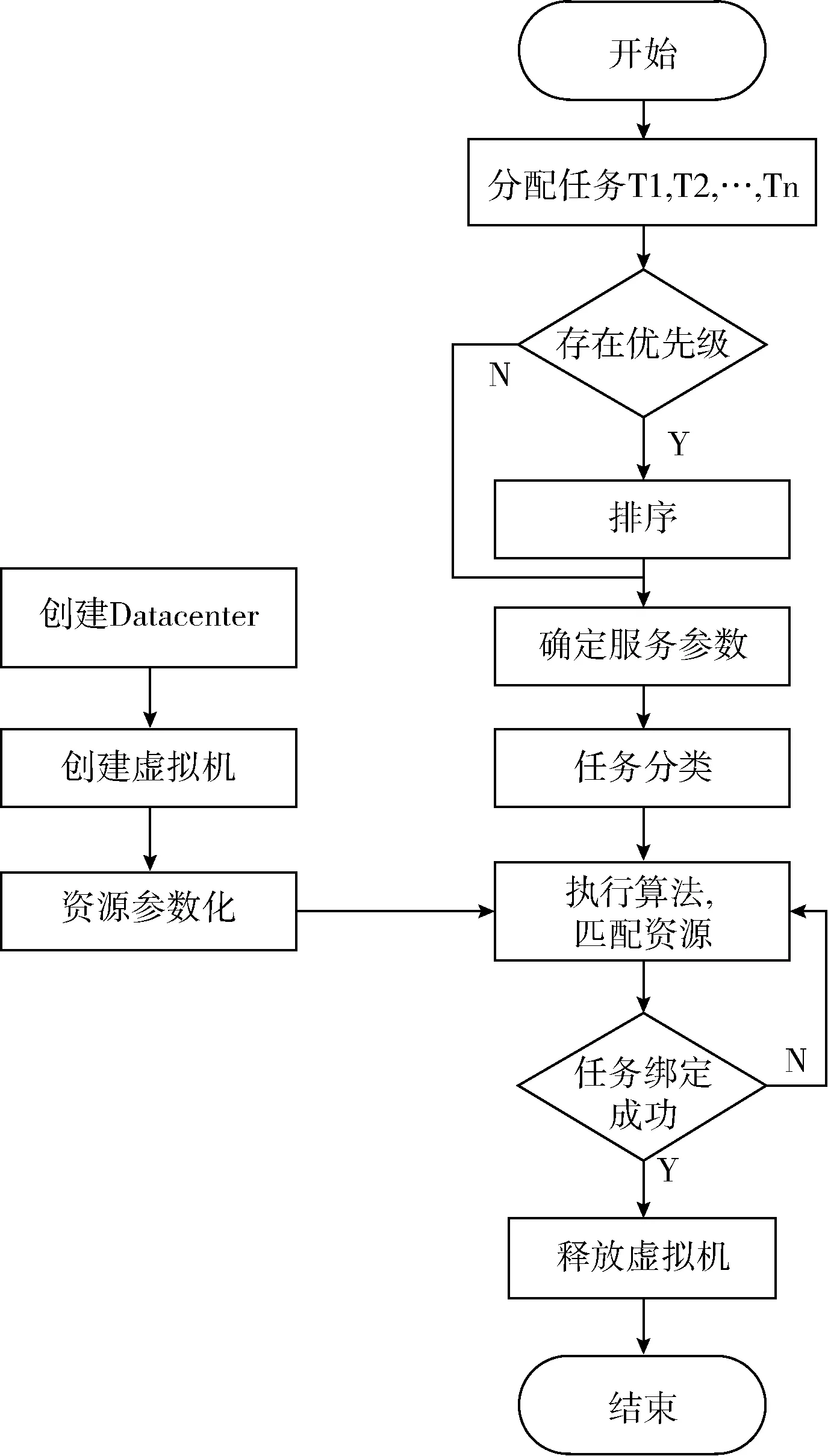
6 结束语
