基于自适应细菌觅食算法的集装箱装载
2018-03-16范霁月张晓庆
范霁月,高 尚,张晓庆
(江苏科技大学 计算机科学与工程学院,江苏 镇江 212003)
0 引 言
针对集装箱装载问题(container loading problem,CLP)[1-3],现在研究者多使用数学规划法、图论法、启发式算法[4]、遗传算法[5]、蚁群算法[6]等来解决集装箱问题,但考虑到装载中存在的约束条件不全面,装载率仍有较大提升空间。细菌觅食算法是近年来新起的一种群智能优化算法,它模拟大肠杆菌的觅食行为,对原始数据进行趋化、复制、消亡操作,进而得到最优解[7-9]。该算法并行性高、处理效率高、鲁棒性强,能以较小的代价通过算法性能获得较大的收益,因此是一种很有价值的解决方法。
本文就集装箱装载问题,提出基于余弦的自适应步长细菌觅食优化算法的求解新方法,在三空间分割装载策略[10]的基础上,使用基于顺序表示的遗传基因编码方式将不同的装载方式编码为适应度函数的解,再通过改进的自适应步长的细菌觅食优化算法[11]得出最优解。相比之前采用的遗传算法、启发式算法、蚁群算法等各种优化算法,实验结果表明,本文中采用的自适应步长的细菌觅食优化算法可以在相对较短的时间内获得一个合理的装载方案,并且有较高的装载率和空间利用率,对实际的装载过程有一定的指导意义。
1 细菌觅食优化算法(BFOA)基本原理
大肠杆菌在觅食过程中逐步向目标移动并且远离有毒物质,这在生物学中被称作觅食方法。细菌在初始位置考量食物的丰富程度后,通过翻滚选择一个随机方向并移动固定的距离,随后再次考量新位置食物的丰富度。一次翻滚和前进过程形成一步趋化。趋化过程中如果下一位置食物更密集,细菌会在同样方向再次游动,直到达到最大游动次数;反之,细菌会翻滚产生新的方向并前进。最大游动次数代表着细菌的生命周期。在细菌生命周期结束时,一半具有较优健康值的细菌在各自的置将被复制,另一半会死亡,复制的执行次数也固定。在寻优过程中我们可以把待优变量和细菌所在位置匹配。细菌复制次数、趋化步数、前进步长、特定方向上的游动次数要根据特定问题初始化,利用BFOA实现变量的最优化。
细菌觅食优化算法是模拟大肠杆菌在我们食道中的吞噬食物行为而产生的新型群体智能优化算法。概括起来主要有4种行为:趋化行为、聚集行为、复制行为和驱散行为。
1.1 趋化行为
趋化过程是由翻滚和前进实现的,是细菌觅食算法的核心。其设计好坏与否直接影响着算法在解决集装箱装载问题上的性能与效果。假设θi(j+1,k,l)表示第i个细菌在第l次驱散、第k次复制、第j+1次趋化的位置,则有
θi(j+1,k,l)=θi(j,k,l)+C(i)φ(j)
(1)
式中:C(i)为翻滚过程中设定的随机方向上的步长,φ(j)为随机方向单位向量。
1.2 聚集行为
通常问题期望细菌寻找到食物最优的路径后能够快速地吸引其它细菌到目标位置。群游(swarming)能够让细菌紧密靠拢,使得细菌在群组中集体移动。群游是所有细菌共同作用的结果,该结果添加到实际目标函数后,表现为变化的目标函数。群游结果的目标函数数学上可表示为
(2)
式中:S是细菌总数量,p是每个细菌需优化的参数个数。吸引剂数值dattract,排斥剂数值hrepellent,吸引剂释放速度ωattract和排斥剂释放速度ωrepellent是待调系数。
1.3 复制行为
为了在优胜劣汰,种群进化的同时,保证种群规模的相对稳定,一部分觅食能力强、健康状况好的细菌,在同样的位置分裂为两个相同个体;健康状况最差的细菌被淘汰。通过复制操作,种群中的优良个体得以保留并得到保护,这样大大提高了寻找最优解的速度,且保持了种群的完整性。
1.4 驱散行为
细菌在局部环境下常受到养料消耗或是环境突变的影响,导致其消亡或者被驱散到别处。这种现象可能破坏趋化过程,但细菌也可能被驱散到好的食物源附近。驱散行为加强BFOA全局寻优能力,降低细菌陷入局部极小现象的可能性。
2 集装箱问题应用
基于BFOA具有容易陷入局部极值、收敛速度慢等缺点,所以本文采用自适应细菌觅食优化算法(ABFOA)解决集装箱装在问题,使用改进的基于余弦的自适应规则的步长替代固定步长,自适应步长随着迭代次数的降低而减小,更好地对细菌进行趋化操作,显著提升算法的寻优质量,在求解CLP上取得满意的效果。
2.1 问题描述
设定集装箱的长、宽、高分别为Lj,Wj,Hj,质量为Mj,容积为Vj待装的n类货物的长、宽、高分别为li,wi,hi,质量为mj。ki为每类货物的总数量。则问题的目标函数为
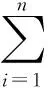
(3)
即:k1*所有装载的货物体积总和占集装箱体积的比例+k2*所有装载物品的质量总和占集装箱最多可承受的质量比例,其中k1,k2为比例系数,一般取值k1+k2=1,参见2.4章节。
式(3)中,F为目标函数;φi为第i类已装货物件数,0≤φi≤ki,为第i类货物总件数,k1和k2为比例系数,两者范围在0-1之间。
装载货物时的约束条件为:
(1)货物的装载容积约束:所有装载的货物体积之和小于集装箱可容纳的最大体积;
(2)货物的装载质量约束:所有装载的货物质量之和小于集装箱可承受的最大质量,公式表示如下
(4)
2.1.1 待装载货物摆放方式
假定待摆放物品是规则的六面体,并且重心在六面体几何中心位置,因此货物在集装箱中产生6种不同的摆放方式。每种待装货物摆放方式的编号分别对应的该货物在集装箱中某种特定的旋转方向,表1是两者之间关系的说明。

表1 待装货物摆放方式编号和集装箱位置对应的关系
2.1.2 空间划分和归并策略
从每个长方体平行但不与HL重合的面装入货物,每当一个货物进入集装箱放置好之后,该货物将整个空间分为除自身以外的3个子空间:上空间、前空间、右空间,如图1所示。而后已放置货物的空间被去除,剩余3个形状为长方体的新的空间。放入下一个的货物时,按照上空间、前空间、右空间的顺序对子空间进行填充。每放入新的货物,则其又产生3个新的子空间。
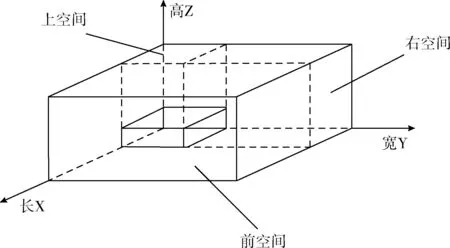
图1 集装箱三维分割
2.1.3 定位规则和定序规则
定位规则中占角策略是指将货物首先摆放在集装箱空间的某一角,通过分析,占角策略是大多集装箱装载问题选择的较好的策略。在定序过程中充分考虑体积和重量综合因素的影响,参照式(3)中k1,k2值,按体积和质量由大到小的定序规则装载货物。
2.2 个体编码和解码
通常,BFOA对解的编码方案大多采用二维或三维空间坐标编码形式,但是对于集装箱装载排序问题显然不采能用该编码方式。原因有二个:①空间坐标可以用于排列质点,但是对于待装载的三维物品很容易在空间上产生交叉现象,为避免该现象不能不引入复杂的计算;②细菌的空间坐标在空间维度上有具体的坐标值,但是不能很好地将其和适应度函数相配,导致算法不宜执行。为此,本文采用基于顺序表示的遗传基因编码方式。将n种待装载物品按照体积和质量由大到小的原则、按自然数由小到大的方式排序编号,并且按照种类编号依次排列编码,则第i个细菌编码形式
Pi=(p1,p2,…,pn,pn+1,pn+2,…,p2n)
(5)其中,i=1,2,…,S,S为细菌种群规模,p1,p2,…,pn为待装货物种类编号,pn+1,pn+2,…,p2n为前n个种类编号对应货物的旋转方向,其值取1,2,…,6。含义见上文。
式(5)中pi和pn+i值相互对应,即第pi种货物以pn+i表示的旋转方向放入集装箱中。利用该解码方式,原有的初始解Pi可以被转化为一个与之相对应的可行解
Qi={q1,q2,…qm,qm+1,qm+2,…,q2m}
(6)
式中:m为待装货物总数量,qi表示等待装载的第i个货物。所有货物根据当前装载状态选择性装入集装箱,货物的编码在可行解中记为1表示其被装入,可行解中为0时表示不装入集装箱。
2.3 自适应步长调整策略
前进步长C(i)对收敛速度和输出误差起着决定性作用。研究发现,BFOA中固定的C(i)会带来两个问题:①若前进步长过大,细菌到达优质点区域的速度虽有所增加,但是会导致寻优精度降低,使得细菌在之后趋化过程中的极值附近来回移动;②若前进步长过小,就会导致细菌到达优质点区域的趋化步数增加。此时收敛速度会降低,迭代步数较少可能使得细菌不能到达最优位置。本文采用特殊的编码和解码方式,将细菌前、后两步趋化坐标Pi中每一维度之差视为前进步长,因此前进步长必须为整数。所以本文改进了文献[11]中的趋向性步长的计算方法,提出新的基于余弦规则的自适应步长,其具有以下特点:
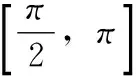
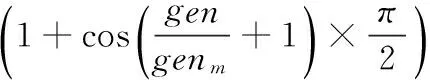
(7)
式中:C(i)和Pi维度一致,C(i)是下取整函数;Cimax为最小步长,Cimax为最大步长,则Cimin≤C(i)≤Cimax;gen为当前迭代次数,genm为最大迭代次数。
2.4 适应度函数
适应度函数是考量个体在目标问题中适应度的函数,它对ABFOA效果起着至关重要的作用。ABFOA中使用适应度这个概念来度量群体中每个细菌所代表装箱方案的优良程度。适应度较高时,代表细菌生命力越强,即种群中的优良细菌,利于存活和复制;而适应度较低的细菌生命力弱,存活概率大大降低。根据2.1节,ABFOA在求解CLP过程中主要考虑到容积率和承载效率,适应度函数形式
(8)
式中:λ为集装箱装载容积率和承载效率的权衡因子,取值范围为[0,1]。
2.5 终止条件
从待装集合Q中取出编号为qi的货物,记录该货物标记,为1表示可以装入集装箱中,无法装入标0:
(1)货物装入时,集装箱空间被分割为上、右、前子空间(如图1所示),放置货物的空间被标记为已用,从空余空间队列中删除,空余空间队列中为3个形状为长方体的新空间。
(2)直到第i个的货物放置时,发现最大的空间仍无法放入,则在货物队列中取i+1货物进行放置,直到可以放入空间内,重复(1)。
(3)当空闲队列中每一个子空间的体积都小于货物队列中体积最小的货物时,则程序停止,跳出。
2.6 算法流程
自适应细菌觅食优化算法求解集装箱货物装载问题流程如下:
步骤1 对每种装载货物按照体积和重量由大到小原则排序并编号,输入每种货物的参数li,wi,hi,mi。
步骤2 初始化权衡因子λ,ABFOA细菌规模S,细菌i的初始位置Pi,驱散次数lmax、复制次数kmax、趋化步
数jmax、特定方向上的游动次数和长度,方向概率PC,吸引剂数值dattract、排斥剂数值hrepellent、吸引剂释放速度ωattract和排斥剂释放速度ωrepellent,j=k=l=0。
步骤3 执行驱散操作,l=l+1,若驱散次数l>lmax,则执行步骤6。
步骤4 执行复制操作,k=k+1,若复制次数k>kmax,则执行步骤3。
步骤5 使用式(1)进行趋化操作,j=j+1,更新并保存适应度函数值。若趋化次数j>jmax,则执行步骤4。
步骤6 选取具有最大适应度函数值的细菌,对其对应的编码进行解码,输出结果,结束。
3 集装箱装载算例和结果分析
实验中算例采用国际上通常使用的标准20尺货柜,尺寸大小为232*92.5*94cm。实验比较了在相同集装箱大小,对相同的货物批次进行装载。待装货物种类20种,每种货物各3-10件不等,货物参数由某物流公司装箱货物尺寸中随机抽取,如表2所示,其长、深、高分别为li,wi,hi,单位为mm,质量为m。

表2 待装货品参数
为评价算法的性能及优越性,采用启发式算法[4]、多目标多种群的随机遗传算法[5]、混合二元蚁群算法[6]和本文中提出的文中提出的基于自适应细菌觅食算法相比较。其中,文献[4]中提出来包含树型搜索子算法和贪心子算法的启发式算法进行空间布局,但是未考虑到装载的约束条件;文献[5]中提出了三维空间切割模型,但为考虑到重量,承载等约束条件;文献[6]中提出了混合二元蚁群算法求解,先用二元蚁群算法确定预备装入货物集,再用启发式算法决定装入优先级顺序,虽大大提升装载率,但算法复杂,时间复杂度较高。实验对3个不同的装箱订单进行装箱实验三维仿真,图2~图4为3次装箱效果,表3为3次装箱的平均计算结果,且各对比算法中的参数设置与原文一致。
装箱订单1中,每种货物取20件,最后共装入货物190件,装载率达到94.76%,结果如图2所示。
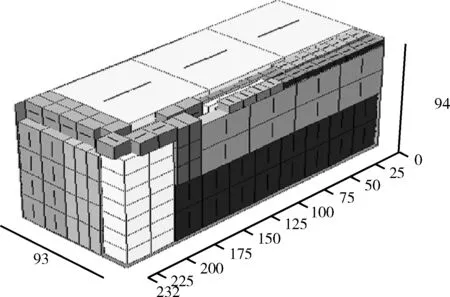
图2 订单1三维装箱结果
装箱订单2中,每种货物随机取1-30件不等,结果共装入货物105件,装载率达到93.69%,结果如图3所示。
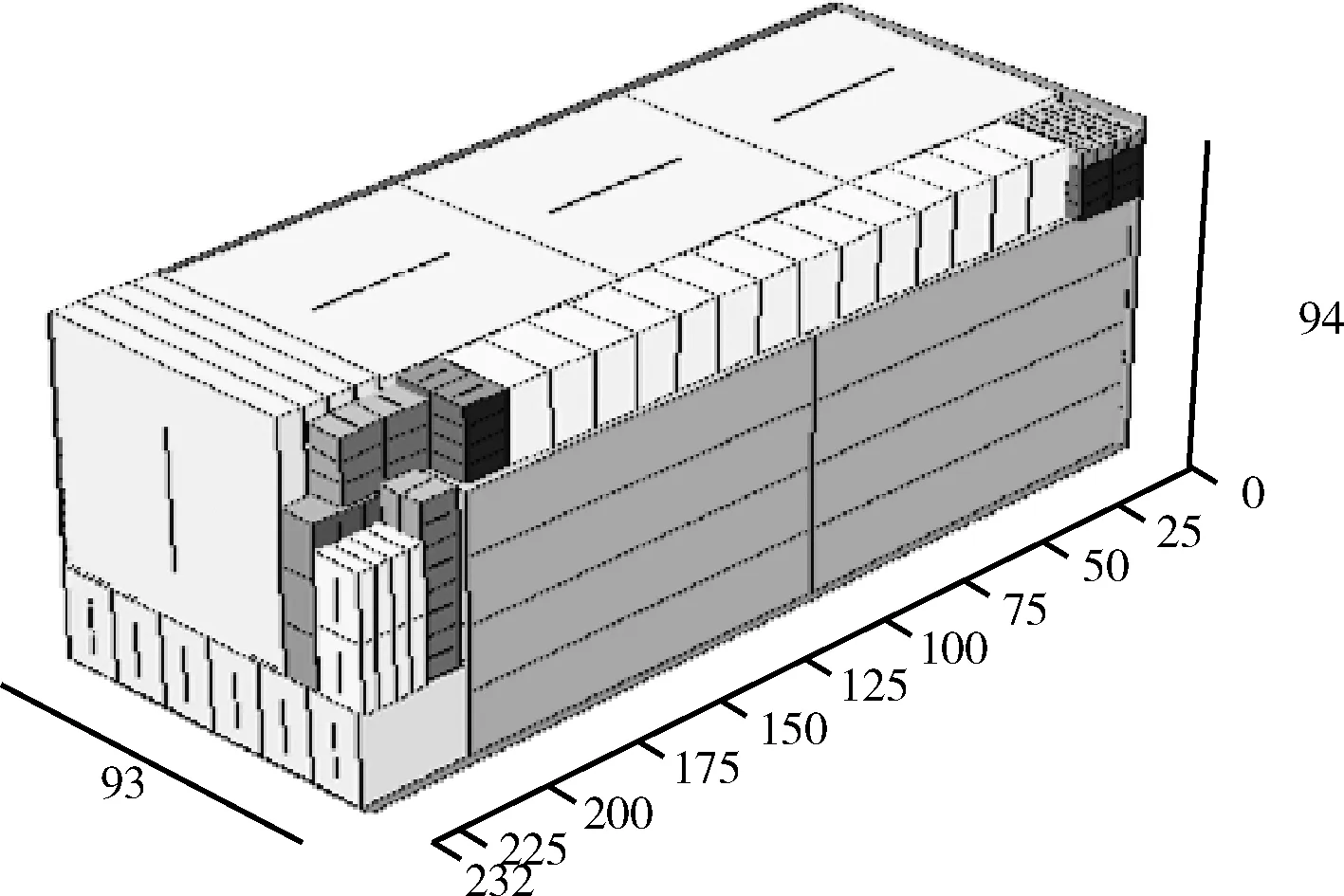
图3 订单2三维装箱结果
装箱订单3中,每种货物随机取1-10件不等,结果共装入货物68件,装载率达到91.76%,结果如图4所示。
实例表明,在细菌趋化过程中极大地降低了细菌游动的复杂性,提升了算法性能,降低了时间复杂度,说明该算法在解决此类三维空间复杂问题上具有优势。与此同时,自适应步长的设置,改善了传统细菌觅食优化算法行进过程中易陷入局部极值的缺陷。在收敛时间上相较启发式算法和蚁群算法也有优势。实验结果中的平均空间利用率为92.07%,和其它3种算法相比较,有了较明显的提升。
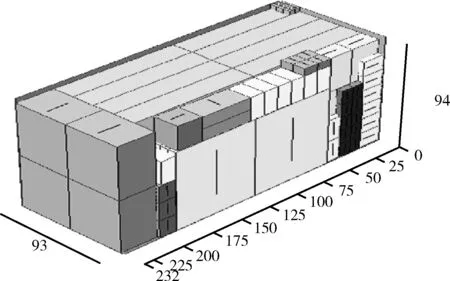
图4 订单3三维装箱结果
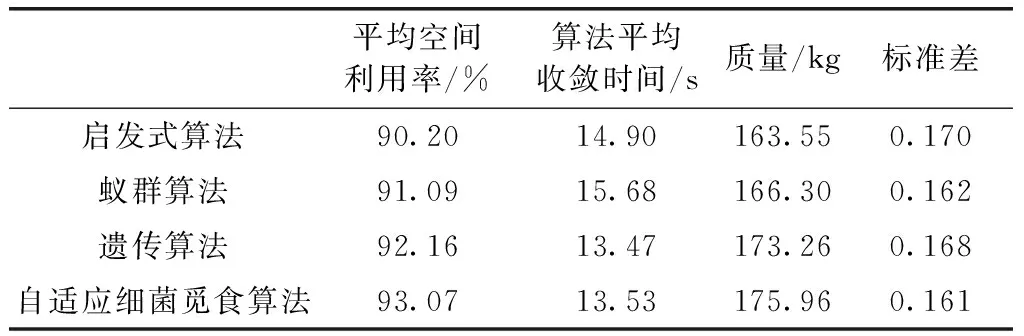
平均空间利用率/%算法平均收敛时间/s质量/kg标准差启发式算法90.2014.90163.550.170蚁群算法91.0915.68166.300.162遗传算法92.1613.47173.260.168自适应细菌觅食算法93.0713.53175.960.161
4 结束语
本文采用了基于顺序表示的遗传基因编码方式,将动态装载问题的各参数与及细菌觅食算法相结合,很好地规避了空间坐标编码的缺陷,在集装箱这类复杂度较高的问题上应用结果良好。改变细菌觅食算法中的固定步长,采用改进了的基于余弦的自适应步长算法,在前期步长大,区域搜索速度快,后期步长小利于局部寻优。在考虑装箱过程中的其它因素,本文对于更复杂的多种类和多约束条件,这也是后续研究的一个方向。
[1]Ramos AG,Oliveira JF,Gonçalves JF,et al.Dynamic stabi-lity metrics for the container loading problem[J].Transportation Research Part C:Emerging Technologies,2015,60(6):480-497.
[2]CHENG Zhongwen.Solving three dimension container loading problem based on space-dividing genetic algorithm[J].Microcomputer Information,2012,54(10):286-287(in Chinese).[程中文.基于空间分割的遗传算法解决三维装载问题[J].微计算机信息,2012,54(10):286-287.]
[3]Liu S,Tan W,Xu Z,et al.A tree search algorithm for the container loading problem[J].Computers & Industrial Engineering,2014,75(2):20-30.
[4]Sheng L,Hongxia Z,Xisong D,et al.A heuristic algorithm for container loading of pallets with infill boxes[J].European Journal of Operational Research,2016,252(3):728-736.
[5]Zheng JN,Chien CF,Gen M.Multi-objective multi-population biased random-key genetic algorithm for the 3-D container loading problem[J].Computers & Industrial Engineering,2015,89(9):80-87.
[6]DU Lining,ZHANG Dezhen,CHEN Shifeng.Solution to complex container loading problem based on ant colony algorithm[J].Journal of Computer Application,2011,31(8):2275-2278(in Chinese).[杜立宁,张德珍,陈世峰.蚁群算法求解复杂集装箱装载问题[J].计算机应用,2011,31(8):2275-2278.]
[7]Peng J,El-Latif AAA,Li Q,et al.Multimodal biometric authentication based on score level fusion of finger biometrics[J].Optik-International Journal for Light and Electron Optics,2014,125(23):6891-6897.
[8]Reddy CHV,Siddaiah P.Bacterial foraging optimization algorithm(BFOA) optimized adaptive hybrid DWT-SVD watermarking with encryption[J].International Journal of Applied Engineering Research,2014,9(24):30911-30933.
[9]Huang YH,Hwang FJ,Lu HC.An effective placement method for the single container loading problem[J].Compu-ters & Industrial Engineering,2016,97(5):212-221.
[10]ZUO Xianliang,GUO Lili,GAO Shang.Improved estimation of distribution algorithm for solving multi-constrained container loading problem[J].Science Technology and Enginee-ring,2014,14(11):216-220(in Chinese).[左先亮,郭莉莉,高尚.改进分布估计算法解决多约束集装箱装载问题[J].科学技术与工程,2014,14(11):216-220.]
[11]LIU Zhen,SUN Jinghao.An improved bacterial foraging optimization algorithm[J].Journal of East China University of Science and Technology(Natural Science Edition),2016,42(2):225-232(in Chinese).[刘珍,孙京诰.一种改进的细菌觅食优化算法[J].华东理工大学学报(自然科学版),2016,42(2):225-232.]
