改进粒子滤波的全捷联导引头制导信息估计*

庞威,谢晓方,刘家祺,孙涛

(海军航空工程学院 兵器科学与技术系，山东 烟台 264001)

0 引言

新型滑翔制导炸弹是在普通航弹上加装被动式红外图像导引头，实现防区外投放和打击目标的。而导引头分为框架式导引头和全捷联导引头：传统框架式红外图像导引头具有较大的视场角，且能够直接提取比例制导等所需的视线角速率信息，但由于框架的存在，结构复杂，成本较高，可靠性较低。随着非制冷红外探测器、CCD探测器等为代表的红外图像制导系统具有结构简单、成本低、设计方便等优点，其在精确制导系统中应用成为目前研究的热点。全捷联红外图像导引头是将光学系统、相机和图像处理模块等直接固联在制导弹药基座上，降低了复杂度和成本，提高了系统的可靠性；采用高分辨率的成像器件提高了角度分辨率以弥补无框架时视场角的降低；但无法直接测量制导所需的视线角速率信息，且由于视场角较大会引入较大的测量噪声，因此需要设计合理的算法对其进行解耦和信息估计。

相关文献已开展了全捷联式图像导引头视线角速率解耦和制导信息估计的研究。Maley James[1]和Jacques Waldman[2]分别采用卡尔曼滤波和扩展卡尔曼滤波(extended Kalman filter, EKF)方法研究了视线角速度估计问题；Smita Sadhu[3]采用扰动观测器研究了视线角速度估计问题；曹卫卫[4]通过构建基于FPGA的硬件卡尔曼滤波系统实现对弹体视线角速度的求导计算；袁亦方[5]提出了一种采用EKF滤波估计方法，用以解决单兵全捷联图像导引头体视线角速度估计问题；孙婷婷[6]通过建立全捷联导引头的数学模型，分别采用微分+稳态卡尔曼滤波方法和无迹卡尔曼滤波方法估计体视线角速度；王小刚[7]采用Huber-Based鲁棒滤波研究了大气层外飞行器捷联导引头体视线角估计问题；张韬[8]提出了一种基于无迹施密特卡尔曼滤波方法，并对落角约束导引律下对机动目标进行了仿真。上述是基于观测噪声为高斯白噪声条件下的视线角速度估计问题，实际上由于导引头和炸弹制作工艺、导引头安装误差、以及大的视场角导致体大量观测噪声等问题，并使其呈现非高斯特性从而导致视线角速度估计精度的降低。

针对上述问题，本文以滑翔制导炸弹中全捷联导引头的应用为研究对象，通过推导视线角速度解耦公式，建立了视线角和角速度的状态模型和观测模型，然后利用改进的粒子滤波算法估计视线角速度，并进行了半实物仿真实验。

1 相关坐标系和角度的定义

1.1 坐标系的定义

为方便提取视线角速率，首先定义本文所需的坐标系。

(1) 地面标系Oxyz

与地表固连，取炸弹投放点在地面的投影点为坐标原点O；弹道面与地面水平面的交线为Ox轴，正方向指向目标；Oy轴沿当地垂线指向天顶；Oz轴根据右手法则定义。

(2) 弹体坐标系Oxdydzd

与弹体固连，取炸弹质心为坐标原点O；炸弹纵轴为Oxd轴，正方向指向炸弹头部；Oyd轴位于炸弹纵向对称剖面内，指向上为正；Ozd根据右手法则确定。

(3) 视线坐标系Oxsyszs

取炸弹质心为坐标原点O；Oxs轴为炸弹和目标的连线，正方向指向目标；Ozs轴位于地面坐标系中Oxz面内，与Oxs轴垂直；Oys轴根据右手法则确定。

(4) 体视线坐标系Oxtytzt

取炸弹质心为坐标原点O；Oxt轴为炸弹与目标的连线，正方向指向目标；Ozt轴位于弹体坐标系中Oxdzd面内，与Oxt轴垂直；Oyt根据右手法则确定。

1.2 角度的定义

qγ为视线高低角：表示视线坐标系中Oxs与地面坐标系中Oxz面之间的夹角。

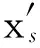
qα为体视线高低角：表示体视线坐标系Oxt轴与弹体坐标系Oxdzd面之间的夹角。

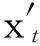
qst为视线变换角：表示视线坐标系Oys轴到体视线坐标系Oyt轴之间的变换角。

ϑ,ψ,γ分别为俯仰角、偏航角与滚转角，其定义参见文献[9]。

各坐标系之间的转换关系如图1所示。其中L(*)表示转换矩阵。

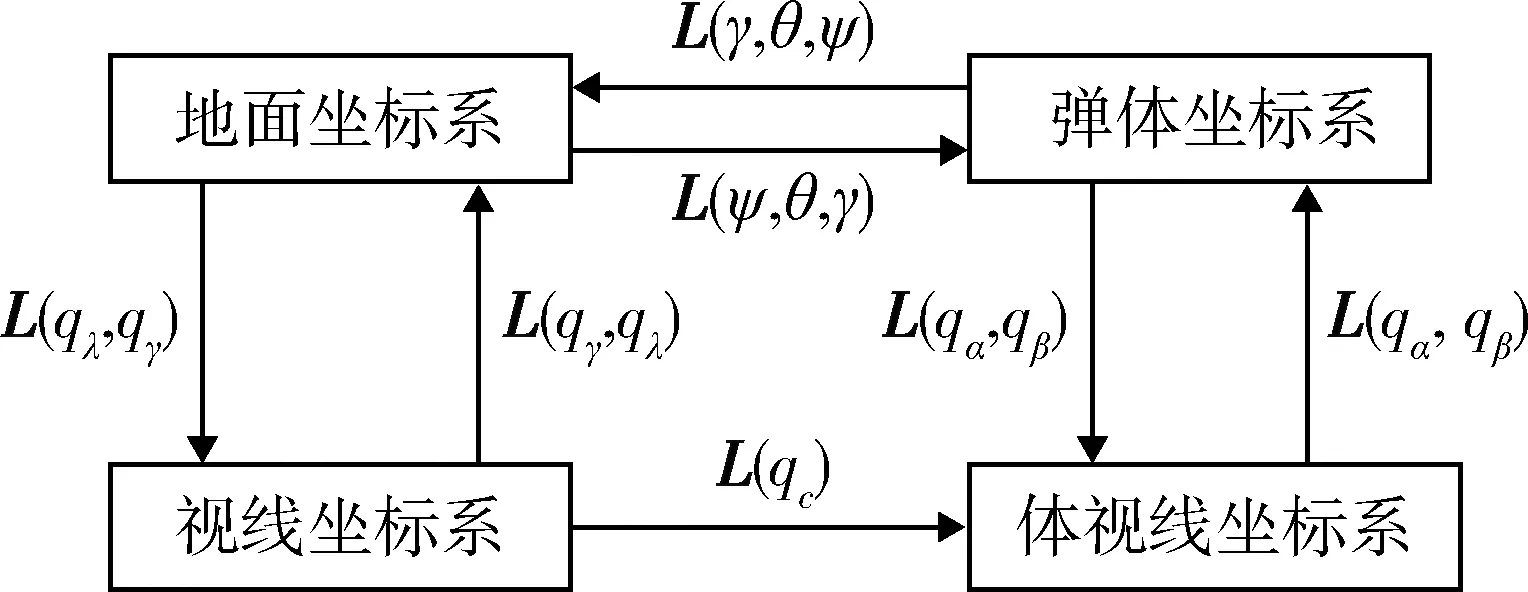
图1 坐标系之间的转换关系Fig.1 Transformation between coordinate systems

2 视线角速度提取

2.1 视线角和角速度解耦方法

滑翔制导炸弹在末制导过程中，弹目相对地面坐标系始终是运动的，全捷联红外图像导引头只能够测量出体视线角的大小，其含有视线角和弹体姿态角，而比例导引方式所需的是视线坐标系下的视线高低角和方位角以及视线高低角速度和方位角速度，因此需要将导引头测量信号中耦合的弹目运动信息去除。

设向量ωd为弹体坐标系相对于地面坐标系3个方向上的旋转角速度，则其在弹体坐标系中可表示为

ωd=(ωx,ωy,ωz)T.

(1)

设向量ωst表示视线坐标系相对于体视线坐标系3个方向上的旋转角速度，则其在视线坐标系中可表示为

(2)

设向量ωtd表示体视线坐标系相对于弹体坐标系3个方向上的旋转角速度，其在弹体坐标系下可表示为

(3)

设向量ωse表示视线坐标系相对地面坐标系3个方向上的旋转角速度，则其在地面坐标系下可表示为

ωse=L(γ,ϑ,ψ)(ωd+ωtd)+L(qγ,qλ)ωst.

(4)

此外，根据视线坐标系和地面坐标系之间的转换关系，ωse也可表示为

(5)

根据式(4)和式(5)可得

(6)

式中：

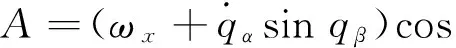
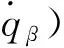
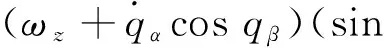
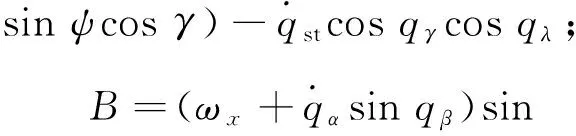
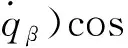
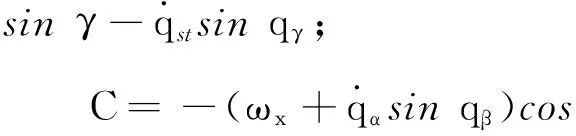
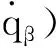
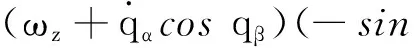
设弹目距离在某时刻为R，由弹目相对运动关系和前文定义的坐标系可知目标在体视线坐标系和视线坐标系上的坐标均为(R,0,0)T，根据图1可得目标在地面坐标系和弹体坐标系中的坐标分别为

(7)

(8)

同时，又根据地面坐标系和弹体坐标系的转换关系，可得式(9)。

(9)

化简,得

式中：

M= -cos ϑsinψcosqαcosqβ+

(sin ϑsinψcosγ+cosψsinγ)sinqα-

(-sin ϑsinψsinγ+cosψcosγ)·

cosqαsinqβ；

N= cos ϑsinψcosqαcosqβ+

(-sin ϑcosψcosγ+sinψsinγ)sinqα-

(sin ϑcosψsinγ+sinψcosγ)·

cosqαsinqβ.

至此，已推导出视线角高低角和视线角方位角度求解公式。

2.2 视线角速度估计模型

全捷联红外图像导引头测量的信息既包含体视线高低角qα和体视线方位角qβ，又包含大量的非高斯噪声[10]；而制导信息为视线高低角、视线方位角和视线高低速度、视线方位角速度，因此本文以这4个量为状态变量建立系统的状态方程。

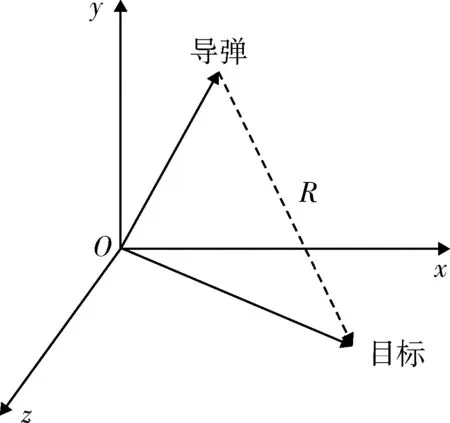
图2 弹目运动关系Fig.2 Relationship between missile and target

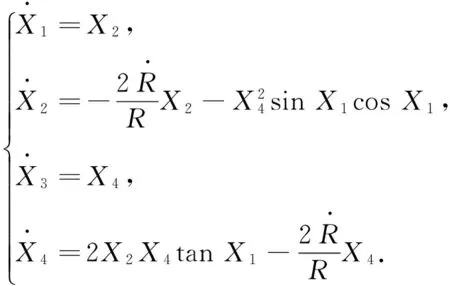
(11)

观测方程为

(12)

式中：

v1和v2为观测噪声。由于全捷红外图像导引头相对于普通导引头具有更大的视场，因此也导致其观测噪声的增大，尤其是非高斯噪声的增大，严重影响了EKF方法的估算精度和稳定特性；同时，从式(11)和(12)中也可看出状态方程和观测方程具有较强的非线性，而粒子滤波对非线性系统、非高斯噪声具有较高的估计精度，因此本文采用粒子滤波求解体视线角速度。

3 基于改进粒子滤波的视线角速率求解

与EKF方法不同，粒子滤波是一种以蒙特卡罗仿真和递推贝叶斯估计为基础的统计滤波方法[12]。其主要思想是首先在状态空间中产生一组以系统状态向量的经验条件分布为依据的粒子集合，并设定粒子的初始权重；然后根据系统的观测值不断调整集合中粒子的权重和位置用以修正初始设定的经验条件分布。其本质是用由粒子集合和对应权重来组成离散随机测度，用以近似系统状态的相关概率分布，然后通过递推算法来更新下一步的离散随机测度。当集合中的粒子数量很大时，这种蒙特卡罗描述即可近似地表示系统状态变量真实的后验概率密度函数。

3.1 标准粒子滤波算法

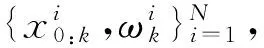
(13)

式(13)中权值可通过重采样法选择，可表示为

(14)

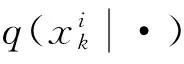
(15)

将式(15)带入到式(14)中，可求得重要权值为

(16)

将权值归一化，即

(17)

式(13)～(17)表示基本粒子滤波中权重的求解方法。采用式(16)求解的粒子权重可能会随着时间的增加，导致重要性权值集中在少数粒子，仅靠这些粒子已经不能够有效地表达出后验概率密度函数，即产生匮乏现象。为克服粒子匮乏，本文提出一种分层采用的粒子滤波算法。

3.2 基于分层采样的粒子滤波算法

分层采样中，将采样空间划分为多个部分，每个部分称为层。在蒙特卡罗积分应用中，把一个积分空间分成几个子空间，然后分别计算每个子空间的积分值。因此，相对于随机采样，分层采样可有效的减少采样误差。

考虑到函数P(x)具有如下的形式：

(18)

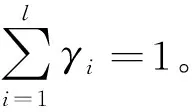
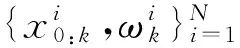
(19)

根据比例分配原则，每层采样的粒子个数为

Ni=floor(Nγi).

(20)

由此，后验概率可近似地表示为

(21)

综上所述，当N→∞时，可由大数定理保证式(21)的值逼近于真实后验概率。

3.3 改进粒子滤波算法步骤

由3.2节，将改进的粒子滤波流程总结如图3所示。

图3 改进粒子滤波算法流程图Fig.3 Flow chart of improved particle filter algorithm

在本文中采用改进粒子滤波的步骤如下：

Step 1:初始化。

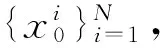
Step 2:重要性采样。

在k时刻，采用式(22)更新粒子权值：

i=1,2,…,N,

(22)

其中:h(·)为测量方程，即式(12)；并采用式(23)对权值归一化：

(23)

那么可得k时刻未知参数x的最小均方误差估计为

(24)

Step 3：分层采样。

选取重要性函数为P(X(k)|X(k-1))，并根据式(11)进行一步预测得到新的粒子集合：

根据分层采样理论，构造出不同层次之间的高斯混合概率密度函数为

(25)

并由此重新获得粒子集合

Step 4:输出结果：k=k+1，转入Step 2。

4 半实物仿真实验与分析

4.1 角速度估计半实物仿真实验

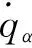
4.2 仿真设置

某新型滑翔制导炸弹采用三维比例制导方式打击目标[14]，末制导启控点坐标为(0,2 000,0)m；初始速度vm0=(100,10,10) m/s,此刻俯仰高低角ϑm0=5.68°；初始航向角ψm0=5.71°，3个方向的初始加速度均为0。目标初始位置为：(400,0,600)m,初始航向角为ψt0=0°，目标作蛇形机动，其运动规律如式(26)所示。

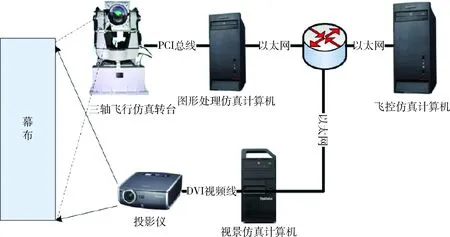
图4 半实物仿真硬件图Fig.4 Hardware of the semi-physical simulation

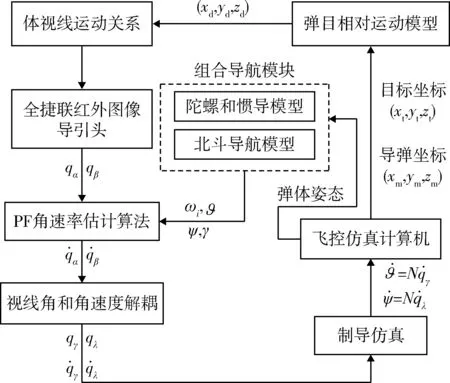
图5 半实物仿真实验原理图Fig.5 Schematic diagram of semi-physical simulation

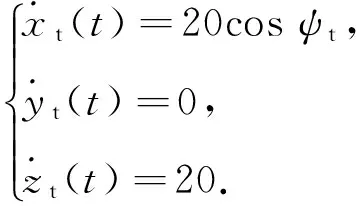
(26)

设定本文的采样时间dt=0.01 s，粒子个数为1 000。为验证本文方法的有效性，同时采用EKF算法[5]、标准粒子滤波方法(particle filter,PF)与理想无干扰理论计算比例导引律作为真值进行对比[15]；攻击目标过程中，末制导方式为比例导引律，其仿真结果如图6～8所示。

定义角度和角速度的均方误差作为算法的评价指标，即

(27)

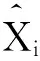
4.3 仿真分析

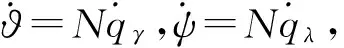
图7表示采用改进粒子滤波得到的视线角和视线角速度的估计值和真值的对比结果。图8表示分

别采用EKF滤波方法和标准粒子滤波(图中PF线)以及本文改进的粒子滤波(图中IPF线)方法得到的滤波误差，表1和表2分别表示采用3种方法得到最大估计误差和均方误差。从表中可以看出,采用改进粒子滤波方法估计精度高于EKF和PF方法。

4.4 原因分析

采用改进粒子滤波方法的估计精度高于EKF和PF方法，主要原因是由于导引头测量的噪声并非高斯白噪声，同时由于组合导航模块中陀螺和惯导测量误差以及三轴转台控制精度等影响，导致观测方程中测量噪声含有大量非高斯噪声；同时由于EKF滤波方法中的状态转移矩阵和观测矩阵采用一阶Taylor展开近似，忽略了二阶以上的高阶项，因此不可避免地引入了线性化误差，从而造成精度的下降。在PF方法中，由于粒子在迭代中发生匮乏现象，造成滤波精度低于改进的粒子滤波方法。

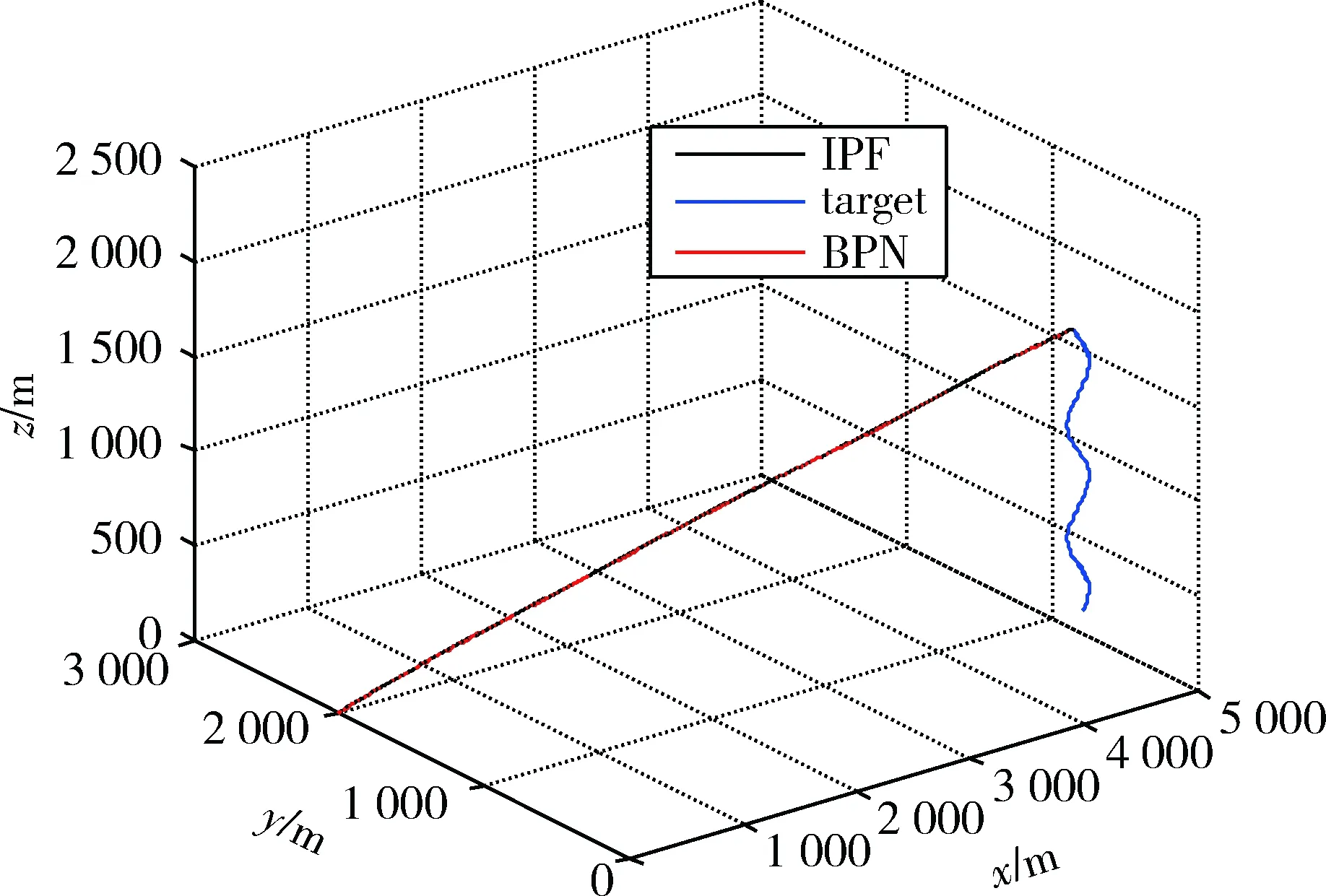
图6 攻击弹道Fig.6 Attack trajectory

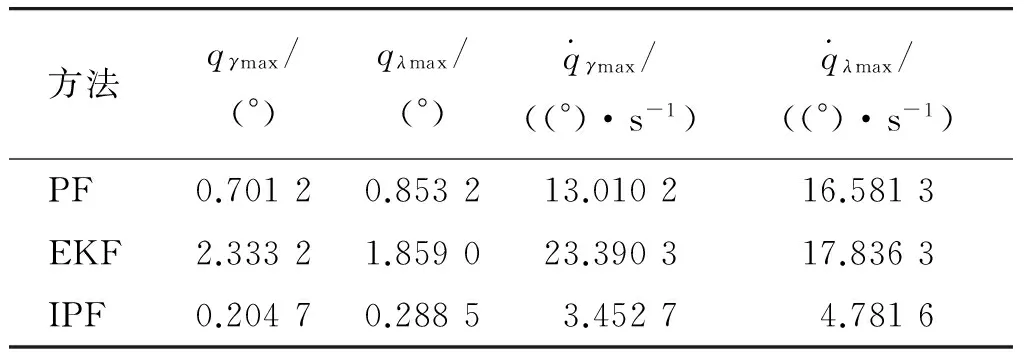
方法qγmax/(°)qλmax/(°qγmax/((°)·s-1qλmax/((°)·s-1)PF0.70120.853213.010216.5813EKF2.33321.859023.390317.8363IPF0.20470.28853.45274.7816

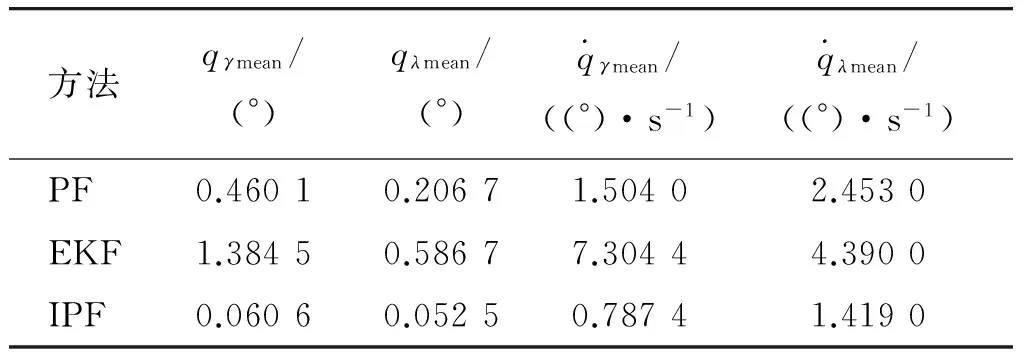
表2 均方误差对比

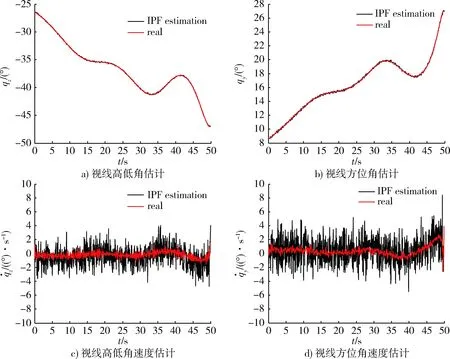
图7 视线角度和角速度估计Fig.7 Estimation LOS and velocity of LOS

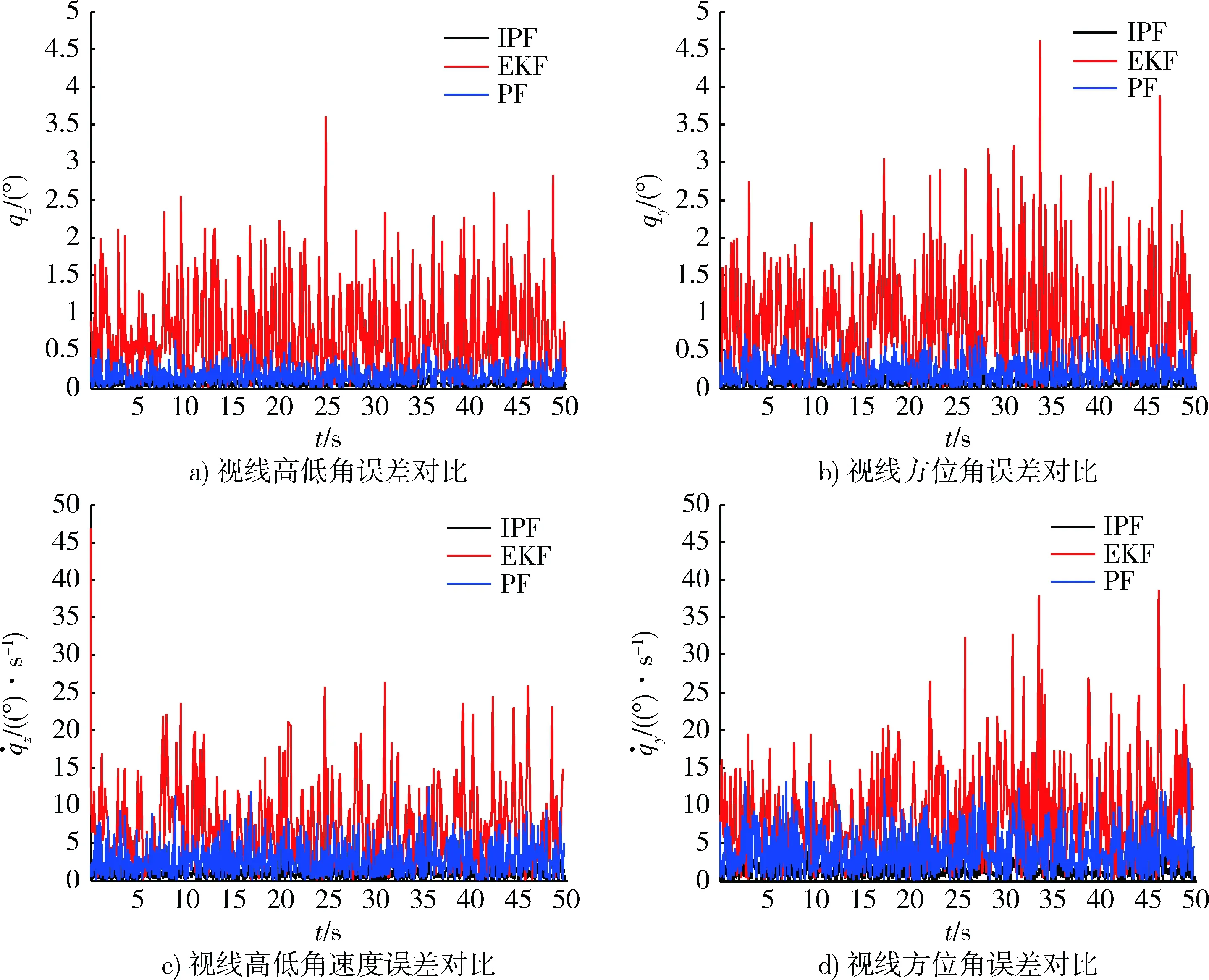
图8 误差分析Fig.8 Error analysis

5 结束语

为加快推进全捷联红外图像导引头在新型滑翔制导炸弹中的应用，本文推导出了视线角和角速度的解耦公式，并提出了基于改进粒子滤波的体视线角速度估计方法，设计了半实物仿真实验进行验证，主要结论如下：

(1) 相比于EKF和PF方法，采用基于改进粒子滤波的体视线角速度估计方法能够得到较高精度的弹目视线角和角速度信息，能满足滑翔制导炸弹对海/地平面攻击所需比例导引律视线角速度的要求。

(2) 半实物仿真实验结果表明：基于改进粒子滤波方法的全捷联红外图像末制导导引头制导信息精度较高，具有较强的实用价值，可为新型滑翔红外图像制导炸弹的研制提供一定的参考。

[1] MALEY J M.Line of Sight Rate Estimation for Guided Projectiles with Strapdown Seekers[J].AIAA Guidance,Navigation and Control Conference,2015,32(6):2346-2351.

[2] JACQUES W.Line-of-Sight Rate Estimation and Linearizing Control of an Imaging Seeker in a Tactical Missile Guided by Proportional Navigation[J].IEEE Transactions on Control Systems Technology,2002,10(4):556-567.

[3] SMITA S,GHOSHAL T K.Sight Line Rate Estimaion in Missile Seeker Using Disturbance Observer-Based Technique[J].IEEE Transactions on Control Systems Tehcnology,2011,19(2):449-454.

[4] 曹卫卫.捷联导引头视线角速率估计方法研究[D].南京:南京理工大学,2012. CAO Wei-wei,Study on Estimation Method of Los Rate of Strapdown Seeker[D].Nanjing:Nanjing University of Science and Technology,2012.

[5] 袁亦方,林德福,祁载康,等.单兵全捷联图像制导弹药制导信息估计技术[J].红外与激光工程,2015,44(1):370-376. YUAN Yi-fang,LIN De-fu,QI Zai-kang,et al.Techniques on Estimating Guidance Information for Strapdown Image Guided Man Portable Munitions[J].Infrared and Laser Engineering,2015,44(1):370-376.

[6] 孙婷婷,储海荣,贾宏光,等.捷联式光学导引头视线角速率解耦与估计[J].红外与激光工程,2014,43(5):1587-1593. SUN Ting-ting,CHU Hai-rong,JIA Hong-guang,et al.Line-of-Sight Angular Rate Decoupling and Estimationof Strapdown Optical Seeker[J].Infrared and Laser Engineering,2014,43(5):1587-1593.

[7] 王小刚,胡智勇,于洋,等.基于鲁棒滤波的捷联导引头视线角速度估计方法[J].中国惯性技术学报,2016,24(2):251-256. WANG Xiao-gang,HU Zhi-yong,YU Yang,et al.Line-of-Sight Angular-Rate Estimation of Strapdown Seeker Based on Robust Filter[J].Journal of Chinese Inertial Technology,2016,24(2):251-256.

[8] 张韬,张希铭,王民钢.全捷联导引头制导信息滤波算法及仿真[J].西北工业大学学报,2015,33(5):744-749. ZHANG Tao,ZHANG Xi-ming,WANG Min-gang.Algorithm and Simulation for Guidance Information Filter for Strapdown Seekers[J].Journal of Northwestern Polytechnical University,2015,33 (5) :744-749.

[9] 李新国,方群.有翼导弹飞行动力学[M].西安: 西北工业大学出版社,2005:28-36. LI Xin-guo,FANG Qun.Winged Missile Flight Dynamics[M].Xi′an: Northwestern Polytechnical University Press,2005:28-36.

[10] 鲁天宇,尹健,夏群利,等.基于波束角误差补偿的相控阵导引头解耦算法[J].系统工程与电子技术,2015,37(9):2123-2128. LU Tian-yu,YIN Jian,XIA Qun-li,et al.A Kind of Decoupling Algorithm of Phased Array Seeker Based on Beam Angle Error Compensation[J].Systems Engineering and Electronics,2015,37(9):2123-2128.

[11] ZHANG Guo-jiang,YAO Yu,MA Ke-mao.Line of Sight Rate Estimation of Strapdown Imaging Guidance System Based on Unscented Kalman Filter[C]∥Proceedings of Fourth International Conference on Machine Learning and Cybernetics,Guangzhou 2005:1574 -1578.

[12] 朱志宇.粒子滤波算法及其应用[M].北京: 科学出版社,2010:27-35. ZHU Zhi-yu.Particle Filter and Its Application[M].Beijing: Science Press,2010:27-35.

[13] 李伟,曹洁,李军,等.噪声相关粒子滤波算法[J].电子科技大学学报,2016,45(3):436-441. LI Wei,CAO Jie,LI Jun,et al.Particle Filter Algorithm with Correlative Noises[J].Journal of University of Electronic Science and Technology of China,2016,45(3):436-441.

[14] 袁宴波,张科,薛晓东.基于Radau伪谱法的制导炸弹最优滑翔弹道研究[J].兵工学报,2014,35(8):1179-1186.

YUAN Yan-bo,ZHANG Ke,XUE Xiao-dong.Optimization of Glide Trajectory of Guided Bombs Using a Radau Pseudo-spectral Method[J].Acta Armamentarii,2014,35(8):1179-1186.

[15] 欧阳中辉,刘家祺,张龙杰,等.基于矢量运算的三维真比例导引弹道仿真[J].弹箭与制导学报,2013,31(1):53-56. OUYANG Zhong-hui,LIU Jia-qi,ZHANG Long-jie,et al.Simulation of Three-Dimensional TPN Trajectory Based on Vector Operation[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,31(1):53-56.