基于功能分配与多目标模糊决策的转向与制动协同避撞控制
2018-03-15严明月魏民祥王可洲赵万忠张凤娇
严明月,魏民祥,王可洲,赵万忠,汪 ,张凤娇
(1.南京航空航天大学, 南京 210016; 2.山东农业工程学院, 济南 250100)
车辆主动避撞系统(vehicle collision avoidance system,VCAS)作为智能交通系统(intelligent transport system,ITS)的组成部分,对于提高行驶安全、预防碰撞事故具有重要的作用[1-2]。纵向制动避撞控制通过降低自车车速避免与前车追尾,但所需避撞安全车距较大[3],若前车突然制动或减速,自车容易因车距较小而不能有效避撞。转向避撞控制在高相对速度、低附着系数等工况下相对于制动避撞控制所需的纵向距离更小,避撞效能更高[4-5]。文献[6]采用四轮主动转向技术来提高紧急避撞时车辆安全性,此方法与传统的两轮转向技术相比,能增大避撞的安全值域。但避撞过程具有多样性,单一转向避撞控制仍存在局限性。例如,车辆通过单一制动控制无法避开自车道前车,即使通过单一转向控制可以避开前车,但如转向的目标车道上前车车速较低,转向时自车易与目标车道前车相撞,因此需要转向与制动协同控制,防止发生斜碰、侧碰、追尾等事故。文献[7]通过两车实际距离与安全距离比较选择一维或二维避撞方式,包括转向辅助、制动、预警或转向与制动协同避撞等,此方法避免了单一避撞方式的局限。文献[8]提出采用非线性模型预测控制算法进行转向与制动协同避撞控制,此方法采用车辆侧向加速度大小来限制车轮转角,保证了稳定性。但文献[7-8]协同控制目标都较单一。
为了避免单一转向或制动控制的局限性,采用一维转向控制和制动控制以及二维转向与制动协同控制3种不同避撞方式,控制车辆在有效避撞的同时期望车辆有较小的纵向位移、较小的横摆角速度和质心侧偏角。针对上述多目标约束问题,采用多目标模糊决策的控制策略,应用功能分配方法确定转向和制动的权重系数,通过仿真验证方法的有效性。
1 系统模型的建立
由于协同控制是面向车辆整个系统进行控制,考虑到模型的准确性,选取CarSim中车辆模型作为整车动力学模型,根据期望的侧向加速度建立逆转向动力学模型,得到期望的方向盘转角,根据期望的纵向加速度建立逆制动动力学模型,得到期望的制动压力。
1.1 转向逆动力学模型
汽车在低速情况下进行转向时,可以忽略轮胎侧偏角的影响,汽车的运动简单地服从“Acklman”转角关系[9],即汽车轨迹的曲率与方向盘转角成正比:
1/R=δ/(il)
(1)
对等式两边同时乘以u2,得:
aMY(t)=uM(t)2/R=uM(t)2δ/(il)
(2)
其中:aMY(t)为自车侧向加速度;δ为方向盘转角;l为车辆轴距;uM(t)为自车纵向速度;i为转向系传动比;R为汽车转弯半径。
因为所研究的线控转向系统换道控制面向的对象都是在较高车速下的车辆,所以必须考虑侧偏角的影响,将式(2)修正为:
δ=aMY(t)il/uM(t)2+aMY(t)ilK
(3)
式中K为稳定性因数,
K=m/l2(l1/k2-l2/k1)
(4)
其中:l1、l2为质心至前后轴的距离;k1和k2为前、后轮胎的侧偏刚度,分别为k1=-1.31×105N/rad,k2=-1.03×105N/rad。
1.2 制动逆动力学模型
根据纵向动力学方程求得期望制动力Fbdes,将Pdes通过执行器加于车辆动力学模型进行制动控制。当车辆处于制动工况时,发动机力矩输出为0,即车辆驱动力Ft为0,则
maMX=-Fbdes-∑F(v)
(5)
其中aMX为自车M纵向加速度。在不超过路面最大制动力的情况下,期望的制动力Fbdes和制动压力Pdes可以近似表示为线性关系,即
Fvbdes=KbPdes
(6)
其中Kb为一系数,是制动力与制动压力的比值。由式(6)得
(7)
其中:CD为空气阻力系数;A为车辆前部有效迎风面积;ρ为空气密度;f为滚动阻力系数。经过在CarSim中进行的车辆制动仿真,得Kb=1 286。
2 避撞安全距离模型
2.1 转向安全距离模型
采用一元五次多项式描述换道轨迹[10],即
(8)
其中:0≤t≤tlat;yM(t)为自车侧向位移;H车辆完成换道过程的侧向位移为3.75 m;tlat换道总时间为2.5 s。由式(8)求导,得侧向速度,即
(9)
由式(9)求导,得侧向加速度,即
(10)
其中0≤t≤tlat。
图1中,自车道有自车M和前车FS,右侧目标车道有一辆右前车FR,本文仅对该3车运动关系进行分析建模。自车通过转向避免与本车道前车发生碰撞,进入目标车道过程中避免与目标车道车辆发生碰撞。考虑换道过程的安全性,换道过程中自车始终在目标车道前车的后面,不进行超车换道,必要时进行减速换道。
设所研究车辆左前角、右前角、右后角、左后角分别为Plf点、Prf点、Prr点、Plr点。自车为M车,前车为FS,右前车为FR。SS(t)为自车M的Plf点与自车道前车FS的Prr点之间的间距,SS0为初始时刻(t=0)自车M的Plf点与自车道前车FS的Prr点之间的间距。SR(t)为自车M的Prf点与目标车道前车FR的Plr点之间的间距,SR0为初始时刻(t=0)自车M的Prf点与目标车道前车FR的Plr点之间的间距。取Plf点为参考点,根据运动学知识得:

(11)

(12)
其中aMX(t)、aFS(t)、aFR(t)、uM(0)、uFS(0)、uFR(0)分别为车辆M、FS、FR的纵向加速度和初始纵向速度。
图2中,t∈[0,tP]时,自车与前车可能发生追尾、斜向碰撞和侧向碰撞。当t∈[tQ,t.lat]时,自车与右前车可能发生斜向碰撞、侧向碰撞和追尾。要保证自车在任一时刻t内与前车和右前车都不发生任何形式的碰撞,则Ss(t)>0且SR(t)>0,由式(11)得自车与前车的最小初始安全距离为

(13)
由式(12)得自车与右前车的最小初始安全距离为

(14)
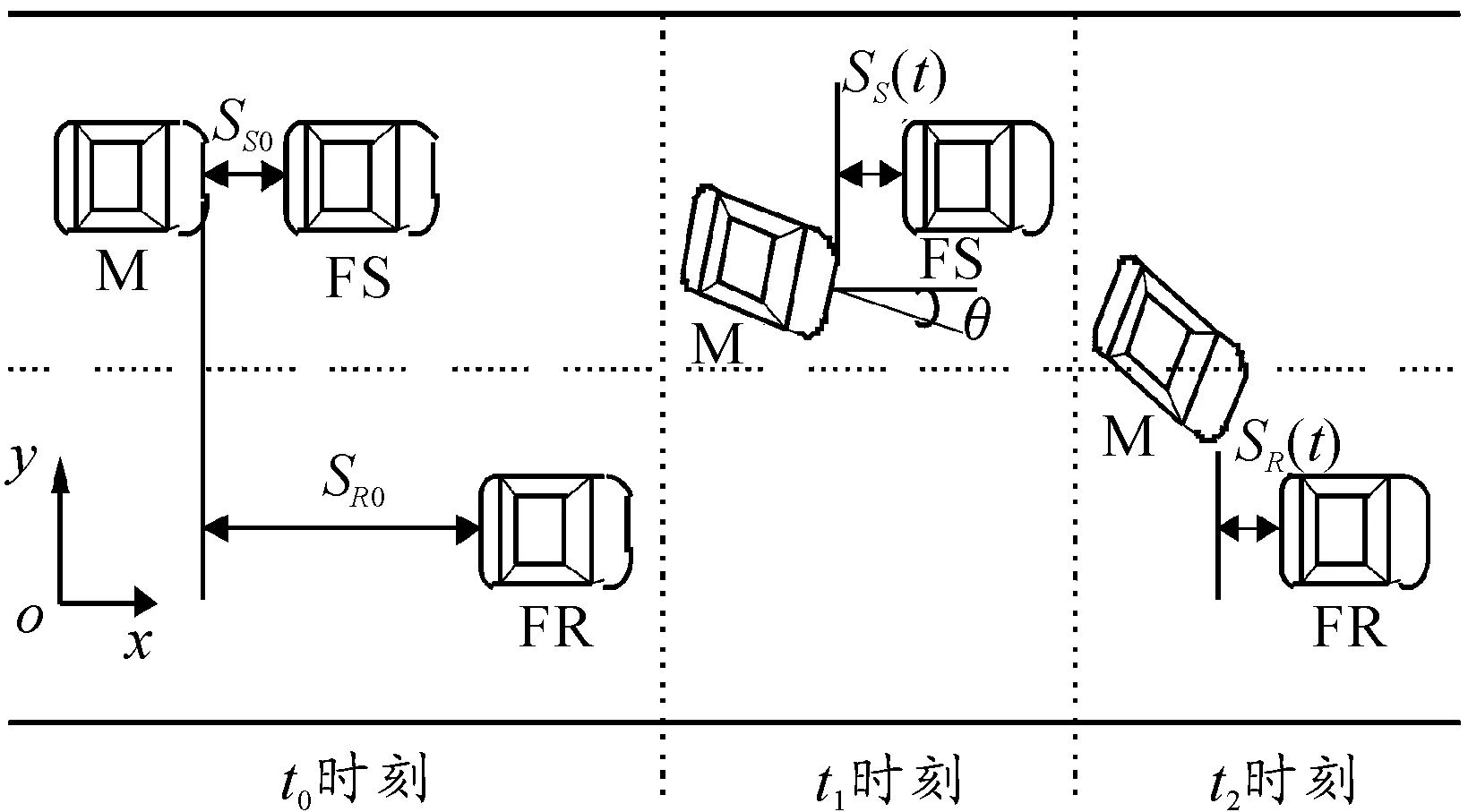
图1 车辆换道运动关系
图2中,自车与前车碰撞点为P点,自车与右前车的碰撞点为Q点。自车与前车在碰撞时刻tP的侧向位移关系为
yM(tP)=yFS+wFS
(15)
其中:wFS为前车车宽;yFS前车侧向位移为零。由式(15)和式(8)可以得到自车与前车的碰撞时刻tP。
碰撞时自车和右前车侧向位移关系为
yM(tQ)+wcosα(tQ)=yFR≅H
(16)
其中w为自车车宽。
(17)
由式(8)(9)(16)(17)得自车与右前车的碰撞时间tQ。
若自车、前车、右前车都纵向匀速, 由式(13)(14)得转向安全距离为:
∀t∈[0,tP]
(18)

(19)
2.2 制动安全距离模型
在行驶过程中,驾驶员根据前方行车状况,接受紧急制动信号后,经过动作并控制车辆减速或停止下来[9]。
(20)
最小跟随距离d0[11]表示自车与目标车辆相对速度为0时所需要保持的车距。当目标车辆静止时,取最小跟随距离为3.6 m。当目标车辆运动时,最小跟随距离为
d0=0.85uFS(t)+1.61
(21)
若前车匀速行驶,自车调整自车速度以避撞。自车位移为
(22)
只考虑自车制动时间,前车位移为
(23)
则临界纵向车距为
(24)
3 功能分配协同控制系统设计
3.1 基于多目标模糊决策的控制策略
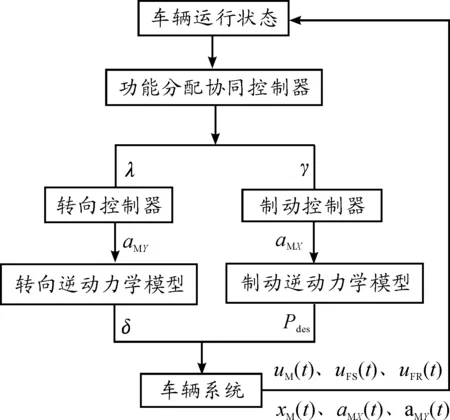
图3 协同控制系统
本文设计了上层协同控制器和下层转向以及制动控制器,功能分配协同控制系统如图3所示。车辆在行驶时通过各种车载传感器实时感知车辆运行状态,功能分配协同控制器判断车辆所处状态,决定避撞方式,控制系统根据自车运行状态按单一制动控制和单一转向控制的有效区域来确定各下层控制器的作用权重。转向权重系数为λ,制动权重系数为γ。下层控制器分别输出期望的侧向和纵向加速度给转向和制动逆动力学模型,将由逆动力学模型得到的期望方向盘转角和制动压力施加给车辆系统,使车辆完成避撞且保持较好操纵稳定性。
车辆需要转向与制动协同控制的典型工况如下:
1) 车辆通过单一制动控制无法避开自车道前车,通过单一转向控制可以避开前车,但转向的目标车道上前车车速较低,转向时自车易与目标车道前车相撞,因此需要转向与制动协同控制,防止发生斜碰、侧碰、追尾等事故。
2) 车辆通过单一制动控制无法避开自车道前车,通过单一转向控制可以避开前车,但转向时自车车速较大,采用单一转向控制车辆稳定性较差,因此需要转向与制动协同控制,防止发生侧滑、侧碰事故。
单一转向控制、单一制动控制和转向与制动协同控制作用的有效区域以及转向权重系数和制动权重系数的取值原则如下:
1) 当S1≥db时,制动系数γ=1,转向系数λ=0。其中S1为自车左前角点与前车右后角点间实际距离。当两车实际距离大于制动安全距离时,通过制动控制即可有效避撞。
2) 当S1
3) 不符合1)和2)条件时选择转向与制动协同控制。协同控制系统采用多目标模糊决策确定功能分配系数。合理选择转向系数λ和制动系数γ对于协同转向与制动实现紧急避撞有关键作用。由于在避撞设计时,在实现多目标控制过程中有一些不确定性,多目标模糊决策的vague集方法在处理不确定性方面具有明显优势,因此采用多目标模糊决策的vague集方法[12-13]来确定λ、γ的范围。
协同控制器使自车有效避开前车和目标车道的前车的目标是:较小的纵向位移、较小的横摆角速度、较小的质心侧偏角,分别用C1、C2、C3表示。则目标集可表示为C={C1,C2,C3}。供选方案:单一转向控制、单一制动控制、转向与制动协同控制,用A1、A2、A3表示。则方案集为A={A1,A2,A3}。
方案Ai可以用Vague集表示为
Ai={(C1[ti1,1-fi1]),{(C2[ti2,1-fi2]),{(C3[ti3,1-fi3]) }
(25)
其中:tij为方案Ai满足目标Cj的程度,即目标Cj属于方案Ai的真隶属函数;fij为方案Ai不满足目标Cj的程度,即目标Cj不属于方案Ai的真隶属函数。tij∈[0,1],fij∈[0,1],tij+fij≤1,i=1,2,3;j=1,2,3。若决策者选择一个方案来同时满足目标C1、C2、C3,则满足这一方案的估计函数E可定义为:
(26)
根据估计函数,定义评价函数
(27)
若J(E(Ai))为最大,则方案Ai是最佳选择,J(E(Ai))∈[-1,1],i=1,2,3。
根据上述的多目标决策理论可知,当满足条件3)时,同时转向制动的避撞策略效果最好,根据多目标模糊决策理论可以得到
J(E(A3))>max{J(E(A1)),J(E(A2))}
(28)
即
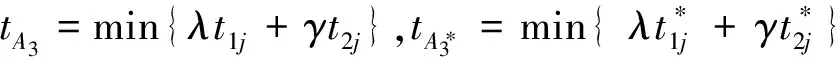
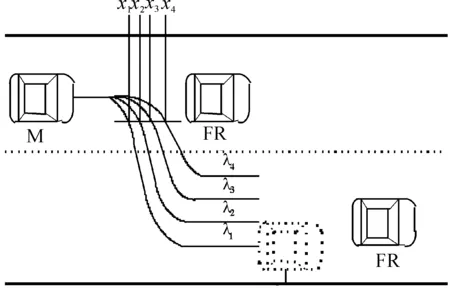
图4 换道轨迹
制动系统采用路面可提供的最大制动力进行制动,因此转向与制动协同控制时制动系数的范围为0<γ≤1。
图4中,改变转向系数λ得到自车M的换道轨迹1,2,3,4,其中λ4<λ3,转向系数的选取原则:
1) 防止自车与前车的右后点碰撞。避撞轨迹(即图中λ3=1轨迹)为恰好避开前车、右前车的轨迹,若自车与前车实际距离等于转向安全距离,则只有λ≥1的轨迹可以使自车避开前车。若自车与前车实际距离大于转向安全距离,即存在余量Δ(余量为实际距离与转向安全距离之差),则可利用此余量增大λ的选取范围。轨迹簇与右前车右侧边缘延长线的交点所对应的纵向位置为x1、x2、x3、x4,若x4与x3的差值小于余量Δ,则轨迹4可以避开前车。因此,λ<1也有可能实现避撞。通过余量利用方式确定转向系数取值下限。通过仿真得到轨迹纵向位移差与转向系数下限的对应关系。

表1 纵向位移与转向系数关系
2) 防止自车撞上最右侧路肩,即图4中5处自车右边缘与右侧路肩间距大于0,由此确定转向系数上限值,通过高速避撞仿真得上限为1.25。
3.2 转向控制器与制动控制器
转向与制动控制器分别采用PI控制。转向控制器的输入为理想侧向加速度与实际侧向加速度的偏差,经过PI调节后输出给逆转向动力学模型。经过仿真调试,P=1.8,I=0.6。制动控制器的输入为理想纵向加速度与实际纵向加速度的偏差,经过PI调节后输出给逆制动动力学模型。经过仿真调试,P=1.5,I=0.8。
3.3 车辆稳定性评价
根据线性2自由度车辆模型可以计算出车辆转向行驶时的理想横摆角速度和质心侧偏角为:
(29)
(30)
式中:K为稳定性因素;δf为前轮转角。

表2 整车参数
4 算法仿真验证
将转向与制动协同控制系统在CarSim和Simulink环境中进行联合仿真,3辆仿真试验车均选用D-Class Sedan车型,整车参数见表2。
仿真条件:路面附着系数为0.8,自车与前车纵向距离为25 m,相邻右侧车道上前车与自车纵向距离为15 m,3车初始时刻质心位于车道中心线上,自车初始纵向车速为110 km/h,初始侧向车速为0,前车纵向匀速车速为100 km/h,右前车纵向匀速车速为85 km/h,前车F和右前车FR在仿真实验过程中无侧向位移。通过功能分配协同控制和单一转向控制对比来验证控制策略的效果。定义Vague集为
A1={(C1[0.9,0.9]),(C3[0.3,0.7]),(C4[0.6,0.4])}
A2={(C1[0.2,0.3]),(C3[0.95,0.95]),(C4[,0.9,0.9])}
通过式(28)以及转向系数与制动系数取值原则,得转向与制动系数值域,如图5所示。值域由3条给定表达式的线段和边界线段λ=1.25,γ=0,γ=1所围成,即图5中区域A所示。经调试取转向权重系数λ=0.85,制动权重系数为γ=0.51。仿真图像见图6~9。

图5 转向与制动系数值域

图7 侧向位移
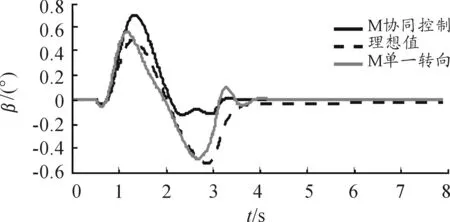
图9 质心侧偏角响应
在图6纵向位移图中:在自车通过单一转向控制过程中,在t=2.25 s时,自车M的纵向位移与右前车FR的纵向位移相同,在图7侧向位移图中,自车M在t=2.25 s时质心侧向位移为-1.12 m,考虑到车宽为1.795 m,自车与右前车已发生碰撞。M车通过协同控制过程中始终与前车FS和右前车FR保持安全距离,且换道轨迹光滑。在图8横摆角速度响应曲线中,自车M单一转向控制过程中的横摆角速度与理想横摆角速度最大瞬态偏差为2.09,自车M协同控制过程中横摆角速度与理想的横摆角速度最大瞬态偏差为0.51,相对偏差同比减少32.6%。这主要由于高速转向车辆横摆角速度较大,转向同时进行制动协同控制可有效降低车速,减小车辆横摆运动,提高了操纵稳定性。在图9质心侧偏角响应曲线中,协同控制过程中自车M的质心侧偏角与理想质心侧偏角最大瞬态偏差为0.39,单一转向控制的质心侧偏角与理想质心侧偏角最大偏差为0.28,换道后期自车M质心侧偏角绝对值迅速减小,主要是由于高速转向同时进行制动协同控制可有效减小车辆侧滑可能性,从而提高了操纵稳定性。
5 结论
1) 仿真结果表明:在单一方式不能有效避撞的紧急工况下,根据双车道多车运动关系建立的安全距离模型进行减速换道控制能有效避撞。
2) 采用多目标模糊决策方法进行避撞决策,仿真结果表明:控制器能够在考虑紧急工况下的3个方案满足决策者需要适合程度基础上给出最优决策方案。
3) 采用功能分配方法进行转向与制动协同控制,仿真结果表明:该方法能够增大汽车紧急工况下避撞的安全域以及提高操纵稳定性。
[1] 李瑾南,万娟,李凯,等.智能交通系统发展及趋势分析[J].工业技术创新,2014(3):374-380.
[2] 王国锋,宋鹏飞,张蕴灵.智能交通系统发展与展望[J].公路,2012(5):217-222.
[3] LIAN Y,ZHAO Y,HU L,et al.Longitudinal collision avoidance control of electric vehicles based on a new safety distance model and constrained-regenerative-braking-strength-continuity braking force distribution strategy[J].IEEE Transactions on Vehicular Technology,2016,65(6):4079-4094.
[4] BEVAN G P,GOLLEE H,O’REILLY J.Trajectory generation for road vehicle obstacle avoidance using convex optimization [J].Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering,2017,224(4):455-473.
[5] HATTORI Y,ONO E,HOSOE S.Optimum vehicle trajectory control for obstacle avoidance problem[J].IEEE/ASME Transactions on Mechatronics,2006,11(5):507-512.
[6] GALVANI M,BIRAL F,NGUYEN B M,et al.Four wheel optimal autonomous steering for improving safety in emergency collision avoidance manoeuvres[C]//IEEE,International Workshop on Advanced Motion Control.USA:IEEE,2014:362-367.
[7] CHEN S L,CHENG C Y,HU J S,et al.Strategy and evaluation of vehicle collision avoidance control via hardware-in-the-loop platform[J].Applied Sciences,2016,6(11):327.
[8] CHOI C,KANG Y.Simultaneous braking and steering control method based on nonlinear model predictive control for emergency driving support[J].International Journal of Control Automation & Systems,2017(22):1-9.
[9] 余志生.汽车理论 [M].5版.北京:机械工业出版社,2012:97-101.
[10] NELSON W.Continuous-curvature paths for autonomous vehicles[C]//IEEE International Conference on Robotics and Automation,1989.Proceedings.USA:IEEE,1989:1260-1264.
[11] 侯德藻,刘刚,高锋,等.新型汽车主动避撞安全距离模型[J].汽车工程,2005,27(2):186-190.
[12] 刘华文.多目标模糊决策的Vague集方法[J].系统工程理论与实践,2004,24(5):103-109.
[13] 张荣芸,黄鹤,陈无畏,等.基于功能分配与多目标模糊决策的EPS和ESP协调控制[J].机械工程学报,2014,50(6):99-106.
