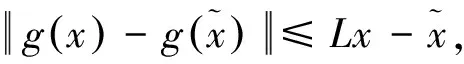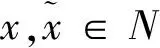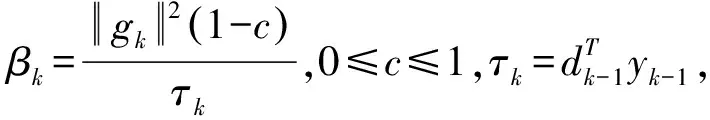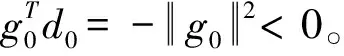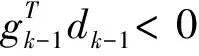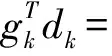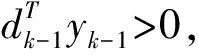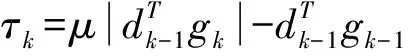一类修正的DY共轭梯度法

陈 恩

(重庆师范大学 数学科学学院， 重庆 401331)

1 背景

考虑如下的无约束最优化问题：

minf(x),x∈Rn

(1)

其中要求目标函数f是连续可微的，它的梯度函数gx是可获得的。

共轭梯度法是解决上面无约束优化问题的最有效方法之一，它的一般迭代格式如下：

xk+1=xk+αkdk

(2)

(3)

其中：αk是通过计算某种线搜索获得的步长；gk=▽f(xk)；βk是共轭梯度法中的一个参数。著名的共轭梯度法有HS方法[1]、FR方法[2]、PRP方法[3-4]、CD方法[5]、LS方法[6]以及DY方法[7]，它们的参数βk分别如下：

其中：||·||为欧几里得范数；yk-1=gk-gk-1。

另外，比较常见的线搜索有标准Wolfe线搜索，它要求步长αk满足：

(4)

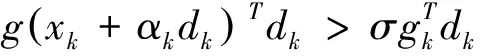
(5)

其中0<δ<σ<1。

共轭梯度算法要求搜索方向满足下降性条件：

∀k≥0

(6)

或者满足充分下降性条件：

∀k≥0,c>0

(7)

2006年，Wei等在文献[8]中对经典的PRP方法进行了修正，提出了如下的参数公式，并证明了该方法在标准Wolfe线搜索条件下对一般函数的全局收敛性：

(8)

2007年，Yao等受文献[8]的启发,在文献[9]中提出了如下两种修正的HS和LS方法：

(9)

2009年，Zhang在文献[10]中进一步修正上面的参数公式为：

(10)

2010年，Wei等在文献[11]提出了一个新的参数公式：

(11)

2011年，江等在文献[12]中进一步修正上面的参数，提出了如下参数公式：

(12)

2 方法的提出

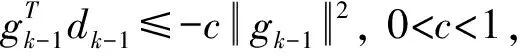
(13)

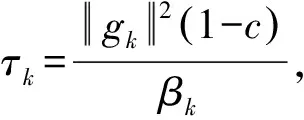
(14)

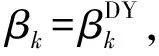
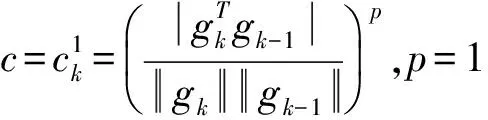
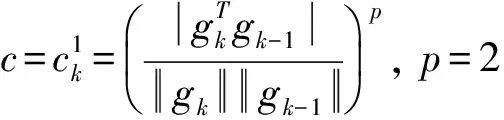
3 收敛性分析

为了获得由式(2)(3)(14)组成的共轭梯度方法的全局收敛性，本文作如下两个基本假设：

1) 水平集Ω={x∈Rn:f(x)

2) 目标函数f在水平集Ω的某个领域N上是连续可微的，并且梯度函数g满足Lipschitz连续，即存在一个常数L>0使得

(15)

(16)

证明完毕。

现给出著名的Zoutendijk条件：

引理2 若假设1)、2)成立，考虑迭代公式为(2)(3)的共轭梯度方法。当方向dk为下降方向，步长αk满足标准Wolfe线搜索的条件时，有

(17)

证明过程见文献[7]的引理3.2。

(18)

因为dk=-gk+βkdk-1，有：dk+gk=βkdk-1。两边同时平方后有：

(19)

(20)

所以有：

(21)

式(21)与Zoutendijk条件的式(17)矛盾，于是定理得证。

[1] HESTENES M R，STIEFEL E.Method of conjugate gradient for solving linear equations[J].J Res Nat Bur Stand，1952，49:409-436.

[2] FLETCHER R，REEVES C M.Function minimization by conjugate gradients[J].The Computer Journal，1964,7(2):149-154.

[3] POLAK E，RIBIERE G.Note sur la convergence de méthodes de directions conjuguées[J].ESAIM:Mathematical Modelling and Numerical Analysis-Modélisation Mathématique et Analyse Numérique，1969，3(R1):35-43.

[4] POLYAK B T.The conjugate gradient method in extremal problems[J].USSR Computational Mathematics and Mathematical Physics，1969，9(4):94-112.

[5] FLETCHER R.Practical Methods of Optimization vol.1:Unconstrained Optimization[M].New York:John Wiley & Sons，1987.

[6] LIU Y，STOREY.Efficient generalized conjugate gradient algorithms，Part 1:Theory[J].Journal of Optimization Theory and Applications，1991，69(1):129-137.

[7] DAI Y H，YUAN Y.A nonlinear conjugate gradient method with a strong global convergence property[J].SIAM Journal on Optimization，1999，10(1):177-182.

[8] WEI Z X,YAO S W,LIU L Y.The convergence properties of some new conjugate gradient methods[J].Applied Mathematics and Computation,2006,183(2):1341-1350.

[9] YAO S W，WEI Z X，HUANG H.A note about WYLs conjugate gradient method and its applications[J].Applied Mathematics and Computation,2007,191:381-388.

[10] ZHANG L.An improved Wei-Yao-Liu nonlinear conjugate gradient method for optimization computation[J].Applied Mathematics and computation，2009，215(6):2269-2274.

[11] WEI Z X，HUANG H D，TAO Y R.A modified hestenes-stiefel conjugate gradient method and its convergence[J].Journal of Mathematical Research with Applications，2010，30(2):297-308.

[12] 江羡珍，马国栋，简金宝.Wolfe线搜索下一个新的全局收敛共轭梯度法[J].工程数学学报，2011，28(6):779-786.