采用概率混合模型的圆周曲线识别方法

杨文彬，杨 明，林守金

(1.中北大学 理学院， 太原 030051； 2.信息探测与处理山西省重点实验室， 太原 030051；3.中山迈雷特数控技术有限公司， 广东 中山 528437)

曲线识别是图像识别和机器视觉的重要研究课题之一。当前常用的方法主要有Hough变换及其各种改进算法、基于目标优化的方法、基于边界跟踪的方法、基于模糊聚类的方法等[1-8]。这些方法各具特色，但也有不同的缺点。基于Hough变换的方法往往计算量较大。基于目标优化的方法往往因为优化方法自身的缺陷导致产生错误的分类结果。边界跟踪方法易受噪声影响。基于模糊聚类的方法往往需要事先给出类别数(曲线条数)。

近些年，国内外学者将概率混合模型用于曲线识别，取得了不错的效果。Fang等[9]利用数据点到待检直线的距离信息构造混合模型，采用EM算法进行参数估计。Long等[10]利用图像中直线段之间的转换关系以及直线段之间的距离构建混合模型，实现对应直线的匹配，从而完成图像的配准。Arellano等[11]采用椭圆上任意两点所在直线的方向和法向等信息建立混合模型，实现了对多个椭圆的识别。

本文依据圆周曲线的几何特征建立相应的混合模型，推导出参数估计方法，并分别用EM算法和贝叶斯阴阳和谐学习算法实现圆周曲线混合模型的模型选择和参数估计，以完成曲线识别。

1 圆周曲线检测的概率模型

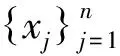
图1 分布在圆周曲线及其附近的随机点

从两个方面分析点集S的分布特点：首先，在圆周方向上表现为均匀分布，这一特点可以由点x与圆心c的连线同x轴正向的夹角θ的均匀性刻画，即假设θ～U(0,2π)(对于圆弧曲线，可假设θ～U(α,β))。其次，点x到圆心c的距离r围绕圆周曲线的半径R波动，可以用正态分布刻画，即假设r～N(R,σ2)。此外，假设θ和r相互独立，这样就可以用随机向量(θ,r)来刻画点集S中每一个点与圆心的关系。

随机向量(θ,r)的联合概率密度函数为

点x的坐标(x,y)与(θ,r)之间的关系为

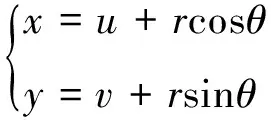
根据

(1)

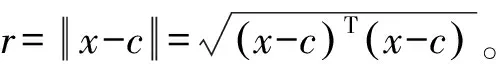
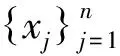
(2)

对式(2)关于各参数求偏导并令其等于0，得到方程组：

(3)

求解方程组(3)即可得到各参数的极大似然估计。其中前2个方程可以直接解得R和σ的表达式，而第3个方程没有解析解，需要用牛顿法等数值方法求解。以下给出参数估计的算法。

算法1 圆周曲线参数的估计方法

输入：数据点xj(j=1,2,…,n)，最大迭代次数K，控制误差ε；

输出：迭代次数k，参数c、R、σ。

步骤1 在允许的范围内随机初始化圆心c(0)，或者随机选取3个数据点，以这3点确定一个圆，该圆的圆心为c(0)，令k←1。

步骤2 若k>K，停止迭代，输出失败信息，否则进行下一步。

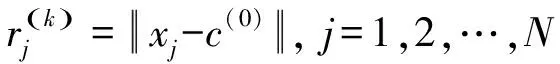
步骤4 计算

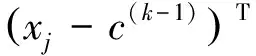
求解关于Δc的线性方程组HcΔc=F，令c(k)=c(k-1)+Δc。

步骤5 若max{||R(k)-R(k-1)||, ||σ(k)-σ(k-1)||, ||c(k)-c(k-1)||}<ε，则停止迭代，输出参数，否则令k←k+1，转步骤2。

2 EM算法检测多条圆周曲线

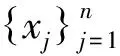
(4)

则分布在多条圆周曲线附近的随机点服从混合概率分布，其概率密度函数为

(5)

其中αi是位于第i条圆周曲线附近的数据点在整个点集中所占的比例，称之为“混合比”系数。参数集为Θ={ci,Ri,σi,αi,i=1,2,…,k}。

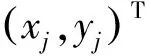
(6)

在EM算法的第p+1次迭代的E(expectation)步中，计算lnLC(Θ)的条件概率EΘ(p)(lnLC(Θ)|X)，也就是计算计算zij的后验概率：

(7)

从而得到M(maximization)步的目标函数：

(8)

(9)

(10)

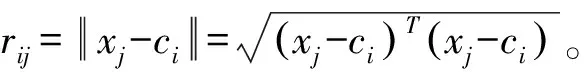
算法2 多条圆周曲线检测的EM算法

输出：迭代次数p，混合比αi，圆周曲线参数ci,Ri,σi，i=1,2,…,k。

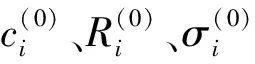
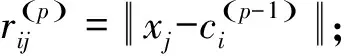
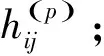
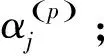
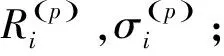
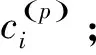
步骤7 若||Θ(p)-Θ(p-1)||<ε，则停止计算，输出参数；否则转下一步；

步骤8p←p+1，若p>P，则停止计算，输出“经P次迭代算法不收敛”的失败信息；否则转步骤2。

3 BYY算法检测多条圆周曲线

考虑到多数情况下待检曲线条数未知，将提出的圆周曲线概率模型与贝叶斯阴阳和谐学习(BYY算法)相结合，以便在曲线条数未知的情况下完成识别。根据BYY算法的理论[12-13]，再结合动态正则化学习[14-15]，构造如下目标函数：

Lλ(Θ)=J(Θ)+λON(p(y|x))

(11)

其中：λ是正则化尺度参数；J(Θ)为圆周曲线混合模型的和谐函数，

(12)

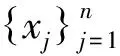
(13)

在式(11)中，如果能够控制λ以一定的策略从0增加到1，最大化Lλ(Θ)的过程就从BYY和谐学习转到极大似然学习的过程，整个正则化学习过程就能在早期的BYY学习阶段实现自适应的模型选择，然后在最终阶段收敛到极大似然估计。

显然，在参数集Θ={ci,Ri,σi,αi,p(i|xj)}上极大化目标函数Lλ(Θ)是很困难的。将参数分为两组：Θ1={p(i|xj)}和Θ2={ci,Ri,σi,αi}，然后用交替迭代寻优的方法求解该优化问题。先固定Θ2，用拉格朗日乘子法解得：

(14)

再固定Θ1，同样用拉格朗日乘子法可以得到：

(15)

求解方程组(15)即可得到各参数估计值。下面给出完整的交替迭代的算法。

算法3 圆周曲线混合模型的BYY正则化算法

输出：迭代次数q、最优分支数k、参数集Θ。

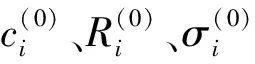
步骤2 按照下面式子更新正则化尺度参数λ：

若|λ(M)-1|<ε1，则停止计算；否则记q←0，进行下一步；

步骤4 按照式(14)计算p(q)(i|xj)；

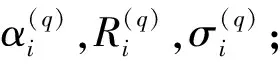
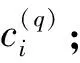
步骤7 若Θ(q+1)-Θ(q)<ε2，Θ(0)←Θ(q+1)，M←M+1，进行下一步；否则转步骤9；

步骤9q←q+1，若q>Q，Θ(0)←Θ(q+1)，M←M+1，返回步骤2；否则返回步骤3。

4 实验

采用3个数值实验和1个真实图像实验来检验算法的性能，实验结果见图2～ 5。图2～ 4是3个数值实验的结果，其中：(a)为实验数据点；(b)为曲线检测结果；(c)为数据点聚类结果。3个实验分别展示了圆之间的3种位置关系：相离，相交和相切。3个实验都取得了不错的检测结果，其中实验1中3个同心圆的检测结果最好；实验1和实验2的聚类结果较好，实验3在2个小圆与大圆相切处的数据点的聚类结果略有偏差。显然，无论对于曲线检测还是数据点聚类，相离是最简单的，而相切是最难的。图5展示了真实图像实验的结果，其中：(a)为原始图像；(b)为经过预处理后去掉背景的灰度图像；(c)为曲线识别结果；(d)为数据点聚类结果。可以看到：对预处理之后的图像，无论是曲线检测还是数据点聚类，算法都取得了理想的结果。

图2 实验1

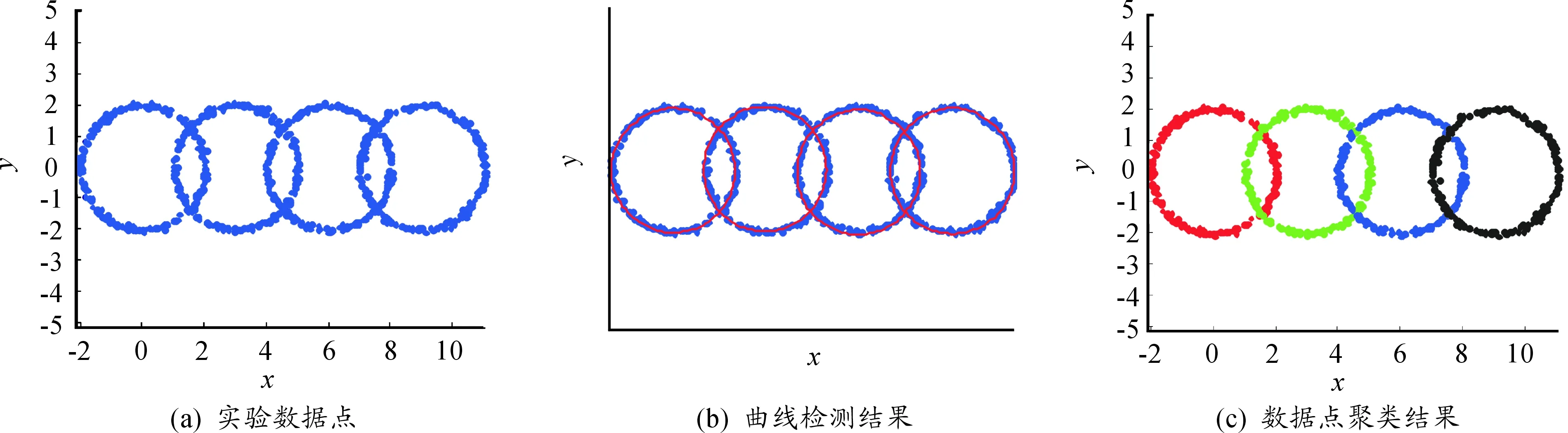
图3 实验2

图4 实验3

图5 实验4

5 结束语

本文根据圆周曲线的几何特征，建立了圆周曲线的有限混合模型，解决了多条圆周曲线的检测问题以及数据点的聚类问题。由于EM算法无法估计曲线条数，故结合贝叶斯阴阳和谐学习算法，在曲线条数未知的情况下实现了圆周曲线识别。实验结果表明：在圆之间相离、相切和相交的情况下，算法都有令人满意的效果，尤其是对于类间有交叉的数据集，一般的模糊聚类算法(如FCM算法、PCM算法)和密度聚类算法(如DBSCAN算法)都无法完成正确的聚类，而本文算法并不受这种情况的影响。另外，该算法完全适用于真实图像中圆周曲线的检测。需要注意的是，应先对目标图像进行图像分割等预处理，提取出待检测的部分，还需要对图像进行适当的缩放。

下一步将进一步改进算法，提高检测和聚类的精度以及计算速度，并将该算法推广到椭圆等更加复杂的图形中。

[1] XU Z，SHIN B S，KLETTE R.Accurate and robust line segment extraction using minimum entropy with hough transform[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society，2015，24(3):813-822.

[2] NG C S.Intelligent hough transform for object detection and tracking[J].Innovative Food Science & Emerging Technologies，2015，5(3):307-316.

[3] MUKHOPADHYAY P，CHAUDHURI B B.A survey of hough transform[J].Pattern Recognition，2015，48(3):993-1010.

[4] 陈小艳，王强，李柏林.改进的Hough变换检测圆方法[J].计算机系统应用，2015，24(8):197-201.

[5] XU G，YANG Y Q，LIU B B，et al.An efficient hybrid multi-objective particle swarm optimization with a multi-objective dichotomy line search[J].Journal of Computational & Applied Mathematics，2015，280(C):310-326.

[6] LI Jin-long，MA Hong-feng，ZHANG W Z，et al.Research on edge detection of track fastener based on machine vision[J].Journal of Northwest Normal University，2017(7):96-101.

[7] SOMKANTHA K，THEERAUMPON N，AUEPHANWIRIYAKUL S.Boundary detection in medical images using edge following algorithm based on intensity gradient and texture gradient features.[J].IEEE transactions on bio-medical engineering，2011，58(3):567.

[8] 石磊，孙凯明，王刚,等.基于模糊聚类的标识点图形识别方法[J].自动化技术与应用，2015，34(12):90-92.

[9] FANG C，MA J.A Fixed-point EM algorithm for straight line detection[M].Berlin:Springer Berlin Heidelberg，2011:136-143.

[10] LONG T，JIAO W，HE G，et al.Automatic line segment registration using gaussian mixture model and expectation-maximization algorithm[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing，2014，7(5):1688-1699.

[11] ARELLANO C，DAHYOT R.Robust ellipse detection with Gaussian mixture models[J].Pattern Recognition，2016，58(C):12-26.

[12] XU L.Best harmony，unified RPCL and automated model selection for unsupervised and supervised learning on Gaussian mixtures，three-layer nets and ME-RBF-SVM models.[J].International Journal of Neural Systems，2001，11(1):43-69.

[13] MA J，WANG T，XU L.A gradient BYY harmony learning rule on Gaussian mixture with automated model selection[J].Neurocomputing，2004，56:481-487.

[14] JIA Y，YANG Z，SONG Q.Experimental study of random dynamic loads identification based on weighted regularization method[J].Journal of Sound & Vibration，2015，342:113-123.

[15] 吕琪.不适定问题的迭代正则化方法研究[D].武汉：武汉理工大学，2012.