基于全局最优解和随机采样的改进人工蜂群算法

施金霄， 熊小峰

（江西理工大学理学院，江西 赣州 341000）

0 引 言

近年来，群体智能已经变成人工智能的一个重要的研究领域．演化算法是研究群体智能的一种方法，该算法不仅有很强的搜索能力而且对优化函数的凹凸性、连续性和可微等特性没有严格的要求．演化算法包括人工蜂群算法（ABC）、差分演化算法（DE）、粒子群算法（PSO）、遗传算法（GA）等．其中人工蜂群算法[1]（Artificial Bee Colony）是由 Karaboga 于2005年提出的一种新的演化算法，算法是受到蜜蜂智能采蜜行为的启发．与其他的一些优化算法相比较而言，ABC算法是解决高维、多峰问题的一种有效的优化算法[2]，其具有操作简单、控制参数少、易于实现等优点[3]．

但是，在求解复杂的问题时，传统的ABC算法存在着求解精度不高、开采能力不足、收敛速度慢等问题，为解决这些问题，近年来许多学者对其进行了改进．例如：Zhu等[4]受PSO算法的启法，在跟随蜂阶段引入全局最优解信息，提高收敛性；Kang等[5]在ABC中运用Rosenbrock旋转方向法，解决在狭小的曲线谷部分的不宜搜索到全局最优解的问题；毕晓军等[6]为解决ABC算法存在的收敛速度慢、易陷入局部最优的问题，改变算法传统的选择机制，并引入OBL策略产生新蜜源代替每次迭代产生的最差蜜源，提出了一种结合NIT技术改进的人工蜂群算法；王慧颖等[7]为提高ABC局部搜索能力和精度,利用全局最优解和个体极值的信息改进搜索模式并引入异步化学习因子保持全局和局部搜索平衡；Gao等[8]受差分演化的启发修改了搜索策略，使其围绕目前的最优解进行搜索，增加算法的开采能力并引入一个新的参数控制搜索方程的选取，提高算法的收敛速度；Karaboga等[9]在跟随蜂阶段引入邻域搜索等式，提高算法的局部搜索能力．刘建军等[10]为提高ABC算法的收敛速度,建立更好地搜索机制和平衡勘探和开采能力,提出了一种在搜索方程中引入个体当前最优解、全局最优解和S型自适应缩放因子以及改变侦察蜂的搜索策略增强种群多样性和随机性的算法；Gao等[11]为解决GABC中解搜索方程震动的问题，利用随机选取个体的方法；Zhu等[12]受BBPSO的启发在跟随蜂阶段引入具有高斯分布的搜索策略，避免了振荡现象最大化了算法的搜索能力．尹雅丽等[13]对标准ABC在求解复杂多峰问题时存在的收敛速度慢、开采能力不足等缺点，提出了方向引导方法和转轴法局部搜索结合的基于转轴法的导向人工蜂群算法，提高了算法的精度．熊小峰等[14]为解决标准ABC求解复杂优化问题出现的收敛的速度慢等问题，提出了精英区域的转轴人工蜂群算法，提高了算法的开采能力，加快了算法的收敛速度．为进一步提高人工蜂群算法的收敛速度和开采能力，提出一个基于全局最优解和完全随机采样相结合的高斯分布的算法．该算法主要有两方面的改进，一方面是利用全局最优解引导和随机采样相结合的搜索方程代替旧的方程，使新的候选解能朝着更好的方向进行搜索并平衡局部和全局搜索能力．另一方面是在侦察蜂阶段利用包含舍弃蜜源信息的高斯等式产生新的蜜源．

1 传统的人工蜂群算法（ABC）

ABC算法是受蜜蜂的智能觅食行为过程启发而提出的一种智能优化算法．该算法根据蜜蜂任务的不同将蜂群分为三种:雇佣蜂、跟随蜂、侦察蜂．雇佣蜂主要负责在蜂巢周围的区域内寻找蜜源并将记录的蜜源的信息分享给跟随蜂．跟随蜂则是在获得蜜源信息后，按一定的概率选择质量较好的蜜源继续开采寻找更好的蜜源并保留．侦察蜂是在一个蜜源已经被耗尽或者找不到更好的蜜源的时候由雇佣蜂转化而来，然后再随机进行搜索得到新的蜜源．在算法设计中雇佣蜂、跟随蜂和蜜源的数量是相等的[1]．

1.1 初始化阶段

ABC算法的初始化方法与其他智能演化算法的机制是相同的，即随机产生SN个蜜源位置．每个蜜源位置信息代表的是优化问题解的信息．初始种群的产生方式如式（1）[1]：

其中，i=1，2， …，SN，j=1，2， …，D （D 为问题的维度），xmaxj，xminj分别表示个体在第j维的上界和下界，rand∈[0，1]为 0，1之间服从均匀分布的随机数．而每个个体以 Xi=（xi1，xi2，…，xiD）来表示．

在初始化之后，ABC算法按雇佣蜂、跟随蜂、侦察蜂三个阶段对蜜源进行搜索，具体操作过程如下．

1.2 雇佣蜂阶段

在该阶段，雇佣蜂按照式（2）在当前的蜜源i周围进行邻近搜索，生成新的蜜源Vi，即Vi=（vi1，vi2，…，viD）：

其中，k∈{1，2，…，SN}，j∈{1，2，…，D}是随机数，并且 k 与 i是相异的，øij∈[-1，1]是随机数．

在雇佣蜂进行邻域搜索过程中，每次只随机更新蜜源位置的一个维度，如果新的蜜源Vi的函数值优于当前的蜜源Xi，则用蜜源Vi代替Xi．

雇佣蜂在进行邻域搜索产生新的候选解后，按式（3）计算新蜜源的适应度值．fiti表示蜜源的适应度值，用其来表示蜜源的质量，而适应值越大表示该蜜源的质量越优，其计算公式为[1]：

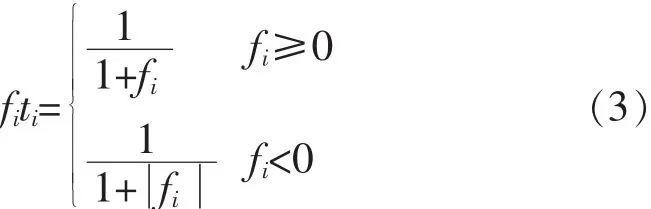
其中fi表示蜜源i的目标函数值．

1.3 跟随蜂阶段

雇佣蜂阶段结束之后，跟随蜂收到雇佣蜂传递的信息，根据蜜源的质量来计算选择概率，然后再根据概率选择一个蜜源进行开采，依据式（4）计算蜜源被选择的概率[1]．

按照式（4）计算概率值，运用贪婪法选择蜜源i后，跟随蜂就在其周围做进一步的搜索即开采，对蜜源进行优化．

1.4 侦察蜂阶段

在侦察蜂工作过程中，如果蜜源的适应度值一直未改变即蜜源的质量未得到提高直到大于预先设定的限制次数“limit”，则这些蜜源就被挑选出来并遗弃．然后按照式（1）随机产生蜜源，再将其作为新的初始蜜源开始进行搜索[1]．

2 改进的人工蜂群算法

ABC算法在求解优化问题时，在对解进行搜索更新的过程中，随机产生的候选解不一定优于现在的解，造成算法收敛速度慢．针对搜索策略存在的低效率问题，引入全局最优解和随机选取解来引导解朝着更优的方向搜索并不失随机性，从而使算法避免早熟或过度的收敛而且使算法的勘探和开采能力得到均衡．为了充分利用搜索经验提高算法的有效性，在侦察蜂阶段引入具有高斯分布的更新等式，加快算法的搜索速度．

2.1 高斯分布搜索策略的改进

为解决ABC算法收敛速度慢的问题，Zhu等[4]受PSO算法的启发，在搜索公式中引入全局最优解（gbest）来引导候选解的搜索方向,以加快算法的收敛速度．然而，单纯地引入全局最优解搜索等式中的两个部分搜索方向会在相反的方向，这样会造成搜索过程中出现“振荡现象”，进而会造成搜索效率变低，算法的收敛速度变慢等问题[12]．

为解决这个问题，受BBPSO更新粒子位置机制[15]的启发提出了基于高斯分布的引入全局最优解的搜索公式，即为：

其中，i=1，2， …，SN，j=1，2， …，D （D 为问题的维度），xbest是当前种群的全局最优解．CR为新引进的控制参数，用来控制每次更新蜜源时改变的维数．

按照式（5）的策略，在处理多峰函数时，有可能会陷入局部最优，而不能搜寻到真正的最优解，如此将会造成算法的早熟收敛．为了尽可能将该问题的影响降到最低，平衡GBABC（Gaussian Barebones Artificial Bee Colony Algorithm）算法的全局和局部搜索能力，考虑利用一个完全随机采样的高斯搜索公式[16]：

其中，i=1，2， …，SN，j=1，2， …，D （D 为问题的维度），r1，r2是两个互异的且不同于 i的[1，SN]之间的随机整数．

由式（6）可以看出，其新解的产生方式是基于高斯分布完全随机采样的，具很强的全局搜索能力．而搜索公式（5）引入了全局最优解引导搜索的方向，使算法的搜索朝着更优地方向进行搜索，有很强地引导性，但式（5）同时会有减弱算法勘探能力的风险，而出现“早熟”的收敛．

为解决上述问题，考虑将式（5）和式（6）两个拥有不同特性的搜索方程结合在一起，又两者都是基于高斯分布的形成方式．故而引入一个权重参数c，通过加权平均的方式把两者组合一起．而c的取值直接会影响算法搜索的方向和结果，当c比较小时，搜索更偏重于朝着由全局最优解引导的方向，当c慢慢增大时，搜索会慢慢偏重于朝着具有完全随机特性的全局搜索方向．因此，权重c值的选取非常重要，为更好的解决复杂优化问题，需要找到一个合适的c值来平衡全局与局部搜索．故而对GBABC跟随蜂阶段搜索公式做出改变，如式（7）．

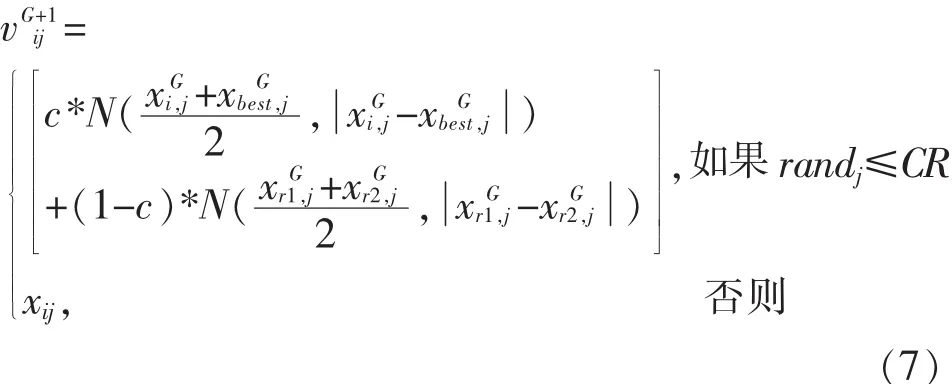
其中，i=1，2，…，SN，j=1，2，…，D（D 为问题的维度），CR=0.3为控制参数，控制每次迭代蜜源改变的维数，c为权重值．

2.2 侦察蜂阶段的改进

在标准的ABC侦察蜂阶段，如果蜜源在达到预先给定的限制次数“limit”不再改善时会被选择出来，然后选择一个蜜源遗弃，每次迭代只有一个蜜源被遗弃，再用随机产生的一个新的蜜源来代替被遗弃的蜜源，这样会造成之前获得的搜索经验流失．为了保留跟随蜂已经搜索到的蜜源的经验，考

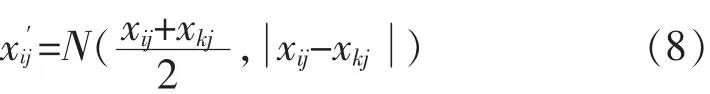
其中，i=1，2， …，SN，j=1，2， …，D （D 为问题的维度），k为[1，SN]之间的随机整数．

按照式（8）产生新蜜源，既保留了将被遗弃的蜜源的经验，又能够更好地利用其周围蜜源信息．为保证得到的新蜜源能够有更好的质量，在利用式（8）产生新蜜源后，根据式（1）随机产生一个蜜源，对两个蜜源进行比较，选择质量更好的蜜源来代替被遗弃的蜜源．

2.3 改进的算法总体框架

MGBABC(Modified Gaussian bare-bones artificial bee colony algorithm)算法是在跟随蜂阶段引入完全随机采样的高斯搜索公式，将其与具有全局最优解引导的高斯搜索方程进行加权，使在求解多峰函数优化问题时能够得到更多有效信息和更好地平衡全局和局部搜索，避免陷入局部最优，提高算法收敛速度和搜索速度．为了很好地利用被遗弃解的搜索经验，在侦察蜂阶段引入高斯方程并且在一代中替换不止一个达到限制次数“limit”仍未被改善的解．在跟随蜂和侦察蜂两个阶段引入具有高斯分布搜索公式，不仅提高了算法的开采能力也提高了收敛速度和求解精度．其算法流程如下所示：

Step1：根据式（1）随机地产生个候选解,{Xi，i=1，2，…，SN}，iter=1，确定最大评价次数 max FES；

Step2:：当FES≤max FES时，执行以下操作；

Step3：雇佣蜂阶段：对于每个蜜源，根据式（2）进行更新产生候选解并计算函数值fi；

Step4：按照式（3）计算适应度值 fiti；Step5：根据式（4）计算选择概率 Pi；Step6：按贪婪法的选择机制从当前种群中选择蜜源Xj；虑引入基于高斯分布的公式产生新的蜜源位置，即为：

Step7：跟随蜂阶段：按照式（7）对蜜源进行更新得到Vj，计算函数值fi和适应度值fiti；

Step8：侦察蜂阶段：对蜜源 i＝1toSN,若蜜源未得到更新的次数triali大于限制次数“limit”，则

triali=0，继续 Step9；否则，返回到 Step2；

Step9：按式（8）产生具有高斯分布的新蜜源x′i，按式（1）随机产生新的蜜源Vi；

Step10：如果f（X′i）＜f（vi），则用X′i代替被遗弃的蜜源 Xi，否则，用 Vi来代替；

Step11：保存当前的最优个体；

Step12：iter=iter+1；

Step13：终止算法．

3 实验及分析

3.1 实验设置

实验中所采用的12个基准测试函数分别来自文献[17]和[18]，它们的名称、取值范围和理论最优值如表1所示，12个基准测试函数中F1,F3为单峰函数，F2,F5～F8,F10～F12 为多峰函数， 当 D＞3时，F4为多峰函数，F9为转移类型的函数．

为了确保比较的公平性，将算法的公共参数作出如下的设置：种群大小SN=30，维数D=30，限制次数 limit=100，函数 F1～F8，F10～F12 最大评价次数为MaxFES=5000*D，F9最大评价次数为MaxFES=10000*D控制参数 CR=0．3，运行次数runtime=30．

3.2 实验结果与分析

在GBABC中引入随机采样的高斯搜索公式和权重c，权重c的大小对MGBABC算法性能会造成影响．为研究不同的权重c的值对MGBABC算法性能的影响，选择最大化算法性能的权重c值，考虑将变量 c值分别设置为 1/4，1/3，1/2，2/3，3/4 五个不同的值．实验结果中，将30次运行求解得到的函数的全局最优值中的最小值和最大值分别记作Min-min、Min-max，其分别反映了函数解的质量的好坏；均值（Mean）为在评价次数一定时算法所达到的计算精度；标准差（Std）表明了算法优化结果的稳定性．

表1 基准测试函数表

为公平比较，所有的函数均是在3.1节设置的参数下进行试验的．并且记录下了每个测试函数的Min-min、Min-max、均值（Mean）、标准差（Std），具体的结果见表2．

表2 不同c值的MGBABC的结果表

对于不同的c值在12个测试函数上的Minmin、Min-max、均值（Mean）、标准差（Std）的最优值已用加粗字体标示．为了从统计学意义上对不同的c值对函数优化的影响进行分析，对得到的最小值、均值和标准差作P=0．05的非参数的Wilcoxon秩和检验．为了研究c值取更大的值对算法性能的影响比较显著还是取更小的值时对算法的性能影响显著，选取c=1/2时得到的结果为参考对象，其中符号“+”表示c为此值时函数最小值（或算法）显著优于c=1/2时的函数最小值（或算法）；“-”表示c=1/2时的函数最小值（或算法）显著优于对应c值的函数最小值（或算法）；“≈”表示两c值对应的函数最小值（或算法）无显著性差异．

对表2中所做的非参数Wilcoxon秩和检验统计得到表3．

表3 非参数Wilcoxon秩和检验结果表

从表3对权重c不同的值对应的函数统计检验结果分析可得：c＝3/4时，算法在函数F12处显著优于其余c值对应的算法，解的精度和稳定性也是较好的；c=1/3时，对应的算法在函数F4和F6处虽然没有得到理论最优值，但得到的解的精度和稳定性是五个c值对应的算法中最高的；c=1/4时，对应的算法除在函数F6问题上显著优于c=1/2时的算法外，其他问题上都不优于c=1/2对应的算法；c=2/3时，除函数F12外，对应的算法均不优于c=1/2时对应的算法；对于函数F6，当c值小于1/2时解的精度和稳定性得到提高，当c值不小于1/2时解的精度和稳定性反而降低了，但c值为1/2时解的质量是最好的；c为1/2时，算法在大部分函数处的性能显著优于或相当于c为其他值时对应的算法的性能．综合考虑，选取c=1/2为修改的算法的控制参数来与GBABC和标准的ABC比较算法的性能．

为了证明在GBABC跟随蜂阶段的搜索策略中引入一个随机采样的高斯搜索公式，能够使算法比两个策略单独进行时优化结果更好．对12个基准测试函数在GBABC、MGBABC和具有随机采样的高斯搜索公式的算法 （在此将该算法记作GBABC1）3个算法，分别进行30次独立实验，实验的参数设置如3．1节，得到函数F1～F12的最小值（Min-min），均值（Mean）和标准差（Std）结果如表 4．

由表4可以看出，算法MGBABC，除了函数F4和F12外，在其他测试函数中,解的质量不逊于GBABC算法的结果，在大部分函数求解中，算法的精度和稳定性得到了提高．除函数F6外，在其他的函数处算法MGBABC的性能均优于算法GBABC1．因此，两个有着局部和全局搜索特点的搜索公式的加权结合，比单个搜索公式对算法的解的质量，精度和稳定性都有一定的改善．

表4 GBABC、MGBABC和GBABC1最小值、均值和标准差结果表

为分析算法MGBABC的性能，对ABC、GBABC、MGBABC算法分别进行30次独立实验进行比较，公共参数SN=30,D=30，limit=100，其余参数详见3.1节参数设置．每个函数的 Min-min、Min-max、均值（Mean）、标准差（Std）的最优值用加粗字体来表示，结果如表5所示．为从统计学意义上分析算法MGBABC结果的有效性，对其进行显著性水平为p=0.05的非参数Wilcoxon秩和检验．其中符号“+”表示算法MGBABC显著优于相应的算法；“-”表示相应的算法显著优于算法MGBABC；“≈”表示算法MGBABC与相应的算法无显著性差异．

表5 算法最小、最大、均值、标准差实验结果表

由于多峰函数的复杂性，存在着许多的局部最优解．记录最小值可以用来与均值进行比较，说明函数的搜索是否陷入了局部最优．

从表5可以看出，MGBABC在绝大部分的测试函数中都能够取得比ABC和GBABC较好的最优值，在大部分的函数处算法性能显著优于或者相当于ABC和GBABC．标准ABC在函数Rosenbrock（F4）和NCRastrigin（F11）处性能显著优于算法MGBABC，对这两个多峰函数算法ABC能比MGBABC更快速的收敛，达到当前的最优解；在函数 Penalized1 （F7）、Penalized2 （F8） 处 ， 算 法MGBABC与标准ABC和GBABC得到相同的结果但没有达到理论最优值，在函数Bohachevsky（F10）处三个算法均取得了理论最优值；在其余的函数处，MGBABC的性能显著优于标准ABC．与GBABC相比，MGBABC 的性能在函数 Sphere（F1）、Schwefel222（F3）和 Rosenbrock（F4）处显著优于算法 GBABC；在函数Ackley（F5）处，GBABC比MGBABC的标准差更小达到了最优，表现更稳定，在函数Zakharov（F12）处，两者表征稳定性的标准差的数量级相同；在其他的函数处，MGBABC和GBABC算法的性能相当．

上述实验结果表明，对于选择的这些测试函数，算法MGBABC在求解单峰函数时，能更快的收敛到全局最优解，求解精度和稳定性也得到显著的提高．在求解多峰函数时，求解的质量有一定的提高，求解精度和稳定性方面明显优于标准ABC的，与GBABC相比，算法的性能有一定的改善．

从以上所有数据来看，在实验设置相同的条件下，算法ABC、GBABC、MGBABC在函数F7和F8处都得到相同的结果，即在实验设置的最大评价次数内均达到了最优值，为进一步分析算法的性能，分别令最大评价次数MaxFES=3000*D，3500*D，4000*D，各个算法分别独立实验30次，实验结果如表6．

表6 函数F7和F8不同评价次数的实验结果表

由表6可以看出，在最大评价次数从3000*D，到3500*D再到4000*D的过程中，算法MGBABC能较快收敛到全局最优值．对于函数F7在最大评价次数为3000*D时，MGBABC就已达到全局最优值，而GBABC和ABC还未达到最优值，对于函数F8，解的质量已达到最优，求解的精度和稳定性相比其他两个算法更高．在求解类似F7和F8的函数优化问题时，MGBABC比GBABC和ABC的收敛速度更快．

为形象地显示提出的修改算法的性能，从12个测试函数中分别选取1个单峰函数，4个多峰函数以及1个旋转函数为代表．利用算法在优化函数时迭代次数和全局最小值两信息，每个函数的维数为10，最大的迭代次数为maxCycle=1000，作出随着迭代次数函数最优值的变化趋势图，如图1所示．

图1 函数最优值选代走势

从图1到图6可以看出，在大部分的函数处，算法MGBABC比GBABC收敛速度较快，而且与标准ABC相比均能很快地收敛．在优化函数时，MGBABC有很强地开采能力和很快的收敛速度．这说明改进的人工蜂群算法在收敛速度方面均有很大的提高，尤其在迭代的前期．

4 结 论

文中为解决标准ABC算法在求解复杂问题时擅长勘探而在开采方面不足的问题，利用引入全局最优解的GBABC算法来进行问题的优化求解，而针对GBABC算法在求解复杂多峰函数时，容易使函数陷入局部最优的情况，提出了一种改进的GBABC算法．该算法主要是在跟随蜂阶段除了具有全最优解进行引导的搜索方程，也引入了完全随机选择的具有高斯分布的搜索策略，平衡了算法在本阶段的勘探和开采能力，有效地进行局部搜索，避免了早熟收敛等．在侦察蜂阶段引入具有高斯分布的新解产生方程，能有效地利用之前的侦察蜂的经验避免有用信息的浪费，提高算法的收敛速度．改进的算法与标准ABC相比有更好的求解质量，求解精度、稳定性和收敛速度也有一定的提高，与GBABC相比，算法的性能有一定的改善．算法中初始化方法、种群大小、雇佣蜂阶段的搜索策略等对性能的影响是不可忽视的，接下来可以对算法的这些方面进行改进，使算法的性能更好，更好地解决复杂函数的优化问题以及现实工程的一些优化问题．

[1]Karaboga D.An idea based on honey bee swarm for numerical optimization[R].Kayseri:Erciyes University,2005.

[2]Karaboga D,Bahriye B.A powerful and efficient algorithm for numericalfunction optimization artificialbee colony (ABC)algorithm[J].Journal of Global Optimization,2007,39(3):459-471.

[3]秦全德，程适，李丽.人工蜂群算法研究综述[J].智能系统学报，2014，9(2):127-135.

[4]Guopu Z,Sam K.Gbest-guided artificial bee colony algorithm for numerical function optimization [J].Applied Mathematics and Computation,2010,217(7):3166-3173.

[5]Kang F,Li J J,Ma Z Y.Rosenbrock artificial bee colony algorithm for accurate global optimization of numerical functions[J].Elsevier Science Inc,2011,181(16):3508-3531.

[6]毕晓君，王艳娇.改进人工蜂群算法[J].哈尔滨工程大学学报,2012，33(1):117-123.

[7]王慧颖，刘建军，王全洲.改进的人工蜂群算法在函数优化问题中的应用[J].计算机工程与应用，2012，48(19):36-39.

[8]Gao W F,Liu S Y.A modified artifical bee colony algorithm[J].Computers&Operations Research,2012,39(3):687-697.

[9]KarabogaD,BeyzaG.Aquickartificialbeecolony(qABC)algorithmand itsperformance on optimization problems[J].AppliedSoftComputing,2014,23(5):227-238.

[10]Liu J J,Zhu H Q,Ma Q,et al.An Artificial Bee Colony algorithm with guide of global&local optima and asynchronous scaling factors for numerical optimization[J].Applied Soft Computing,2015,37(12):608-618.

[11]Gao W F,Liu S Y,Huang L L.A novel artificial bee colony algorithm based on modified search equation and orthogonal learning[J].IEEE Transactions on Cybernetics,2013,43(3):1011-1024.

[12]Xinyu Z,Zhijian W.Gaussian bare-bones artificial bee colony algorithm[J].Soft Computing,2016,20(3):907-924.

[13]尹雅丽，熊小峰，郭肇禄.基于转轴法的导向人工蜂群算法[J].江西理工大学学报，2015，36(5):98-103.

[14]熊小峰，尹雅丽，郭肇禄，等.精英区域学习的转轴人工蜂群算法[J].四川大学学报（工程科学版），2016，48(5):124-134.

[15]Kennedy J.Bare bones particle swarms[C]//Swarm Intelligence Symposium,2003.SIS'03.Proceedings of the 2003 IEEE.IEEE,2003:80-87.

[16]Gao W F,Huang L L,Lui S Y,et al.Artificial bee colony algorithm with multiple search strategies[J].Applied Mathematics&Computation,2015,271(22):269-287.

[17]Yao X,Liu Y,Lin G.Evolutionary programming made faster[J].IEEE Transactions on Evolutionary Computation,1999,3(2):82-102.

[18]García S,Molina D,Lozano M,et al.A study on the use of nonparametric testsforanalyzing the evolutionary algorithms’behaviour:a case study on the CEC’2005 special session on real parameter optimization[J].Journal of Heuristics,2009,15(6):617-644.