基于相关性加权的K-means算法

刘建生， 吴斌， 章泽煜

（江西理工大学理学院，江西 赣州 341000）

0 引 言

聚类分析作为一种识别无符号标记的重要挖掘技术手段，在数据挖掘领域中得到了有效的应用.根据不同的应用领域，人们研究出了不同的聚类算法.其中最主要的有基于层次、基于网格、基于密度、基于模型以及基于划分的算法.在这几种聚类算法中，以基于划分的算法更为被人们所常用，基于划分的算法是一种动态的数据挖掘方法，常以对象间的距离作为划分标准.K-means算法作为基于划分的算法中最具代表性的一个聚类算法，最受人们所欢迎.K-means算法因其简单高效的特点，被广泛地应用于图像分割、病毒入侵检测等领域中[1].K-means算法虽有着诸多优点，但也存在着诸多不足之处.首先，传统K-means算法对于初始聚类中心的选取敏感，不同的初始聚类中心可能产生不同的聚类结果[2]；其次，难以体现样本间的相关性[3].

针对传统K-means算法中存在的不足，大量改进的K-means算法被提出.对于初始聚类中心的改进，文献[2,4]提出K中心点算法，K中心点算法首先为每个类随机选择一个初始对象，将剩余对象归为与代表对象距离最近的类中，然后通过代表对象与非代表对象之间的相互替换，改进聚类的效果；文献[5,6]中的HK-means算法是先对部分样本进行聚类，将所得聚类中心作为初始聚类中心，再对所有样本进行聚类分析；文献[7]提出Rt-kmeans算法，该算法将最大最小初始化法与密度相结合，从而克服初始化随机的问题．除这些改进的算法以外，许多学者将K-means算法与其它智能算法融合集成．文献[8]的GWO-KM算法，该算法将灰狼优化算法与K-means算法相结合，使用灰狼优化算法全局搜索能力强的特性来克服传统K-means算法初始化随机的问题；文献[9]提出一种改进的K-means蚁群聚类算法，该算法对基于觅食原理的蚁群算法引入变异操作，然后与K-means算法相结合，一定程度上改善了现有K-means蚁群算法易陷入局部最优的缺点；文献[10]将人工蜂群算法与K-means算法相结合，通过在迭代过程中利用人工蜂群算法优化聚类中心，从而提高算法收敛时间以及降低算法对初始聚类中心的依赖性．

当前，对于考虑样本间相关性改进的算法研究成果主要应用马氏距离来体现数据集的相关性[3]．但计算马氏距离存在一定的限制，马氏距离考虑的是样本集与样本集间的相关性，并非所有数据集都能计算马氏距离[11]．聚类过程中相同类中样本间相关性的强弱是体现聚类效果的一个重要指标．因此，增强相同类中样本间的相关性是聚类过程中不可忽视的因素．

文中在分析传统K-menas算法及改进K-means算法的基础上，提出了一种基于相关性加权改进的K-means算法．该算法引入具有放缩因子的皮尔逊相关系数，重新定义了样本间距离的计算方法，较好地实现了在聚类过程中增强相同类中样本间的相关性，通过实验对比显示文中提出的算法具有良好的聚类能力．

1 K-means算法理论基础

K-means是典型的基于距离的非层次聚类算法，是将给定的数据集划分到用户指定的k个类中．该算法的实现与运行都非常简单，并且具有运算速度快、易修改等特性，因其简单高效等原因被广泛应用于各领域中．K-means算法作为一种无监督的实时迭代型聚类算法，一般采用所有的类内距离之和作为评价函数，式（1）为评价函数J的定义式．

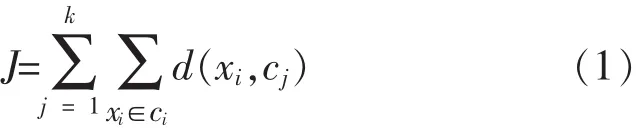
K-means算法如下[12-13]：

算法输入：数据集 X={x1，x2，…，xn}，聚类中心数k

算法输出：聚类中心 C={c1，c2，…，ck}

Step1：从整个数据集X中，随机选取k个数据对象作为初始聚类中心；

Step2：分别计算每个数据对象xi到聚类中心ci的距离 d（xi，cj）,并将数据对象分配到距离最近的类中；

Step3：计算每个类中所有对象的平均值作为新的聚类中心；

Step4：重复步骤Step2～Step3，直到聚类中心不再发生改变或达到最大迭代次数时停止．

K-means算法不足之处：

1）聚类中心数目k的选取困难,相同类中的对象相关性得不到体现；

2）不同的初始聚类中心可能产生不同的聚类结果；

3）K-means算法本质上是一种面向非凸代价函数优化的贪婪下降求解算法，仅能获得局部最优解[12]．

2 CK-means算法

通过对传统K-means算法的分析，针对传统K-means算法中所存在的缺点，提出了一种基于相关性加权改进的 K-menas算法（CK-means）．CK-means算法的主要设计思想有：①通过对最大最小初始化法的改进，获得稳定的，尽可能均匀分布的初始聚类中心，有效地克服了传统K-means算法初始化随机造成的聚类结果不稳定的缺点；②为增强相同类中样本间的相关性，在对样本间距离计算的过程中，引入了皮尔逊相关性系数作为样本间距离的相关性放缩因子．使得聚类过程中欧式距离较大，但相关性较强的对象能被划分在相同类中；而欧式距离稍小，但是相关性很低的对象将被划分在不同的类中．使得相同类中的对象具有更强的相似度，而对于不同类之间对象具有更强的差异性．为清晰说明文中提出关于相关性加权距离思想的合理性以及可行性，文中通过一个假设示例来进行说明．假设存在一组已知类别数据对象A={3 2．3 1},B={3 1-2},C={3 2 4}，其中A、B为一类，C独自为一类．经计算得A、B间距与A、C间距几乎相等，但A、B间的相关程度较高．如果用传统K-means算法聚类，即采用欧式距离来进行度量，所得结果A、C为一类，B独自为一类，与实际结果有较大出入．如果通过相关性对距离加权，最终计算得A、B为一类，C独自为一类，所得结果与假设结果一致．由此证明了文中提出思想的合理性与可行性，Ck-means算法具体为如下两部分．

2.1 初始聚类中心的改进

传统K-means算法初始聚类中心敏感，因此一种有效的初始化方法则必不可少．最大最小初始化法[14]通过选取每类中距聚类中心最远对象作为下一个聚类中心，该方法所选聚类中心绝大部分分布在边界上，而边界上的对象往往是不能代表聚类中心．为此，文中在最大最小初始化的基础上对初始聚类中心的选取进行改进．新产生初始聚类中心与已选初始聚类中心关系如图1所示．图1中cj是已选初始聚类中心，xmax是cj中距聚类中心最远的数据样本（xmax绝大部分属于边界样本）．新产生初始聚类中心应处于已选聚类中心和边界样本之间，相邻两类之间的界值到两聚类中心的距离应相等，且聚类中心应处于所属类别的中心，所以d（cj，t）=2×d（t，xmax）．因此，可计算得 t=cj+（xmax-cj）．据此构造文中初始聚类中心的选取方法如下．

图1 初始聚类中心关系

Step1：计算数据集X的平均值x，令距平均值距离最远样本为xmax；

Step3：计算 Nλ（xi）的平均值，将距平均值最近样本作为第一个初始聚类中心c1；

Step4：对于剩余样本，将其与已选择最近的聚类中心归为一类；xi表示未被选择的样本，cj表示已被选择的初始聚类中心．

Step5：搜索每类中距离聚类中心最远的样本xmax；xmax表示所有类中距离聚类中心最远的一个样本．

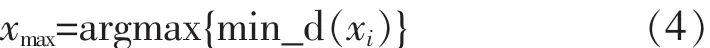
Step6：令 t=cj+（xmax-cj），以 t为中心 λ=d （cj-xmax）为邻域半径内的所有样本为 Nλ（xi）；

Step7：计算 Nλ（xi）的平均值，将距平均值最近样本作为下一个初始聚类中心cs；

Step8：重复 Step4～Step7，直到找到 k 个聚类中心停止．

通过使用该初始化方法，从而使得初始聚类中心尽可能的分布在各自的类中，而不是分布在数据集的边缘．

2.2 Pearson相关系数加权

为了使相同类中的对象具有更强的相关性，文中引入Pearson相关性系数对样本对象间的欧式距离进行加权．为此定义具有相关性缩放因子的距离公式：

其中 cor （xi，xj） 表示 xi与 xj的皮尔逊相关系数，Max_cor、Min_cor分别表示数据集中不同样本间皮尔逊相关数系数绝对值最大值与绝对值最小值，g（xi，xj）表示 xi与 xj归一化后的相关系数，d（xi，xj）表示xi与xj的欧式距离，文中Q值取1，0．01为了防止 g（xi，xj）为 1 时样本间距离为 0，dis（xi，xj）为文中定义的经相关性加权以后xi与xj的距离．

CK-means算法如下：

算法输入：数据集 X={x1，x2，…，xn}，聚类中心数k

算法输出：聚类中心 C={c1，c2，…，ck}

Step1：从整个数据集X中，按照2．1的方法选取初始聚类中心；

Step2：按式（5）分别计算每个样本对象xi到聚类中心 ci的距离 dis（xi，cj），并将该对象归入聚类最近的类中；

Step3：计算每个类中所有对象的平均值作为新的聚类中心；

Step4：重复步骤Step2～Step3，直到聚类中心不再发生改变或达到最大迭代次数时停止．

3 实验仿真与分析

为了验证文中提出的算法的有效性及合理性，在相同软硬件环境下应用相同数据集与传统K-menas算法、GWO-KM算法、Rt-kmeans算法在聚类准确度、收敛时间、评价函数的最大值、最小值、平均值及其标准差六方面进行实验结果比较．

3.1 实验说明及评价标准

仿真的硬件环境：AMD phenom CPU 2．6GHz，内存4GB，软件环境为MATLAB 2009a．实验所用数 据 集 为 UCI 数 据 库 中 的 iris、 （Statlog）heart、sonar以及wine数据集，四组数据集各属性如表1所示．

表1 实验数据集

聚类的准确率能有效的评价聚类效果和聚类算法性能的优劣．purity评价法[15]是一种评价聚类效果的常用方法，purity计算如式（6）所示．

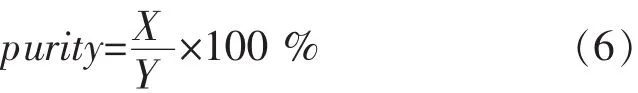
其中，X表示正确聚类对象数，Y表示聚类集合对象的总数．

3.2 实验结果分析

文中的验证过程分为三步．首先是对公式（5）中Q取值的合理性进行验证，通过选取不同Q值对4组数据集进行聚类比较．其次，对文中选取的6个评价指标进行分析，设置算法最大迭代次数T=300次．实验中聚类的准确率、收敛时间及其平均值均通过20次单独实验结果后，取其平均值，结果见表3～表6．第三，对文中的初始化聚类中心方法及相关性加权对于聚类效果影响的验证．

在初始化聚类中心验证中将文中方法与随机初始化法、最大最小初始化法进行了比较；验证相关性加权对于聚类效果的影响时，选取iris数据集对文中算法、传统K-means算法、GWO-KM算法、Rt-kmeans算法进行实验验证比较.图2与图3是iris数据集经主成分分析（PCA）方法降维处理后的实验结果.

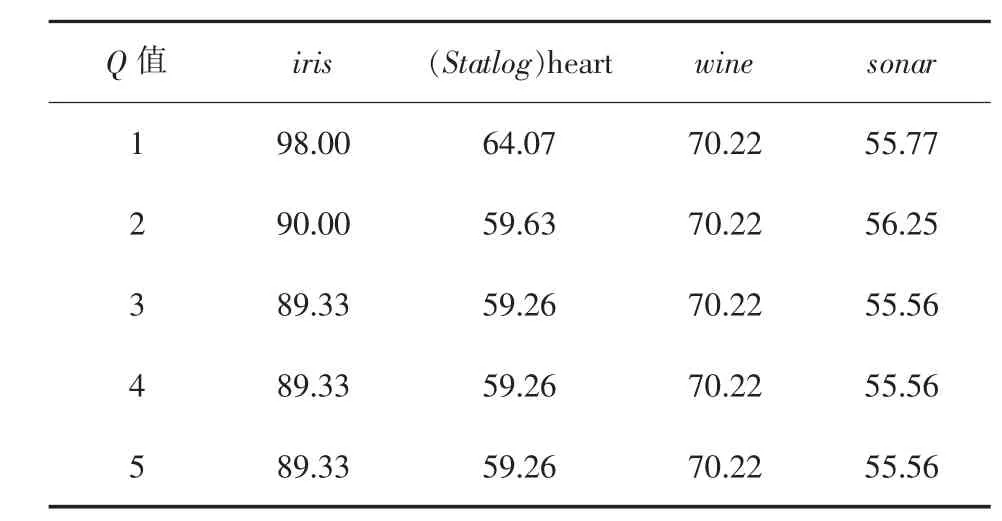
表2 4组数据集在不同Q值时的准确率/%

表3 iris数据集实验结果

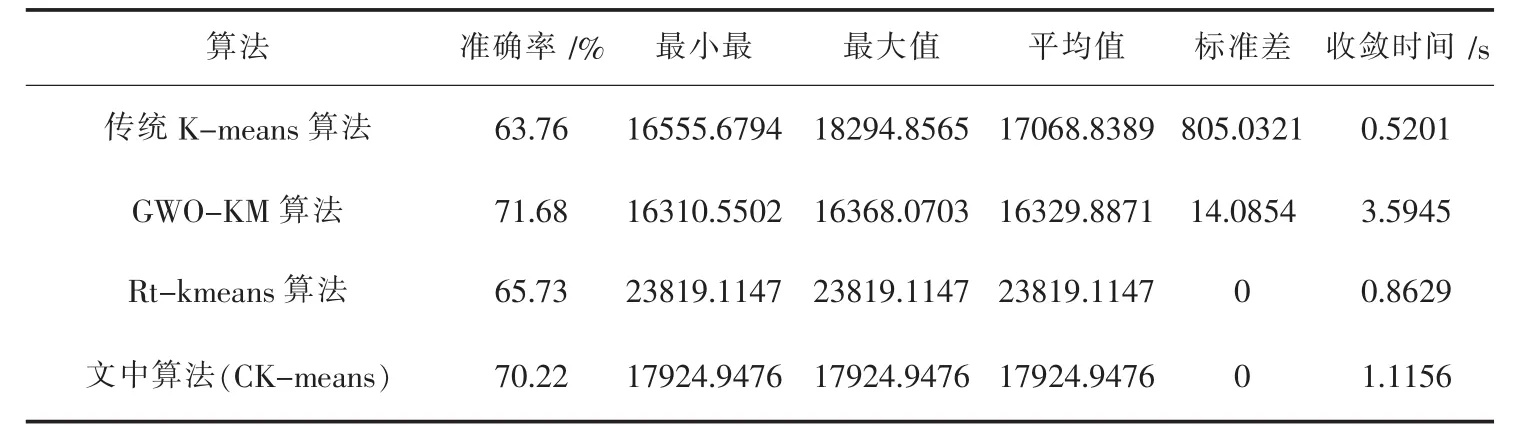
表4 wine数据集实验结果

表5 （Statlog）heart数据集实验结果

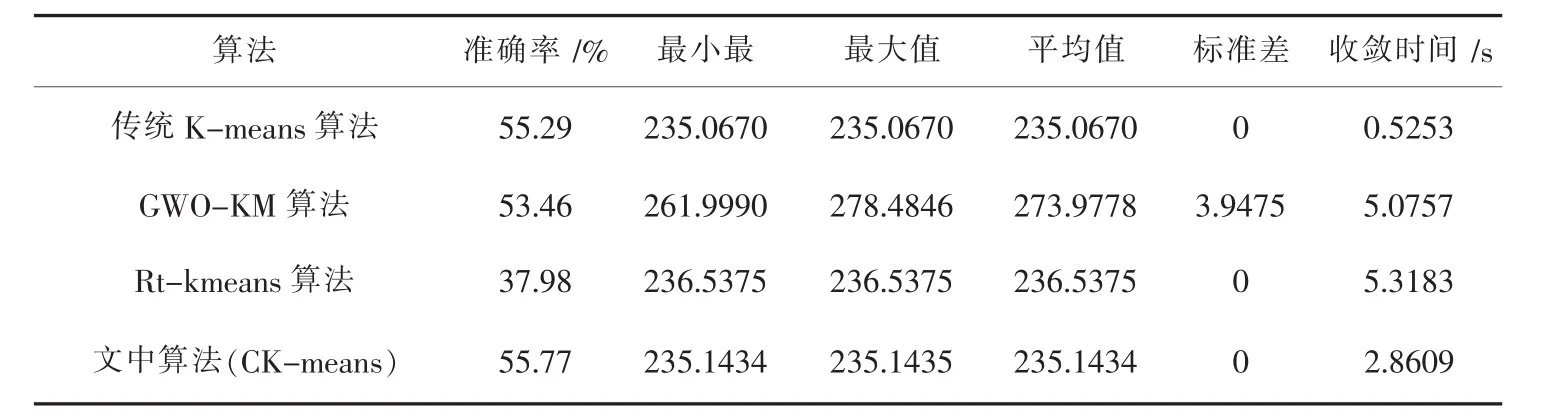
表6 sonar数据集实验结果

图2 初始化效果

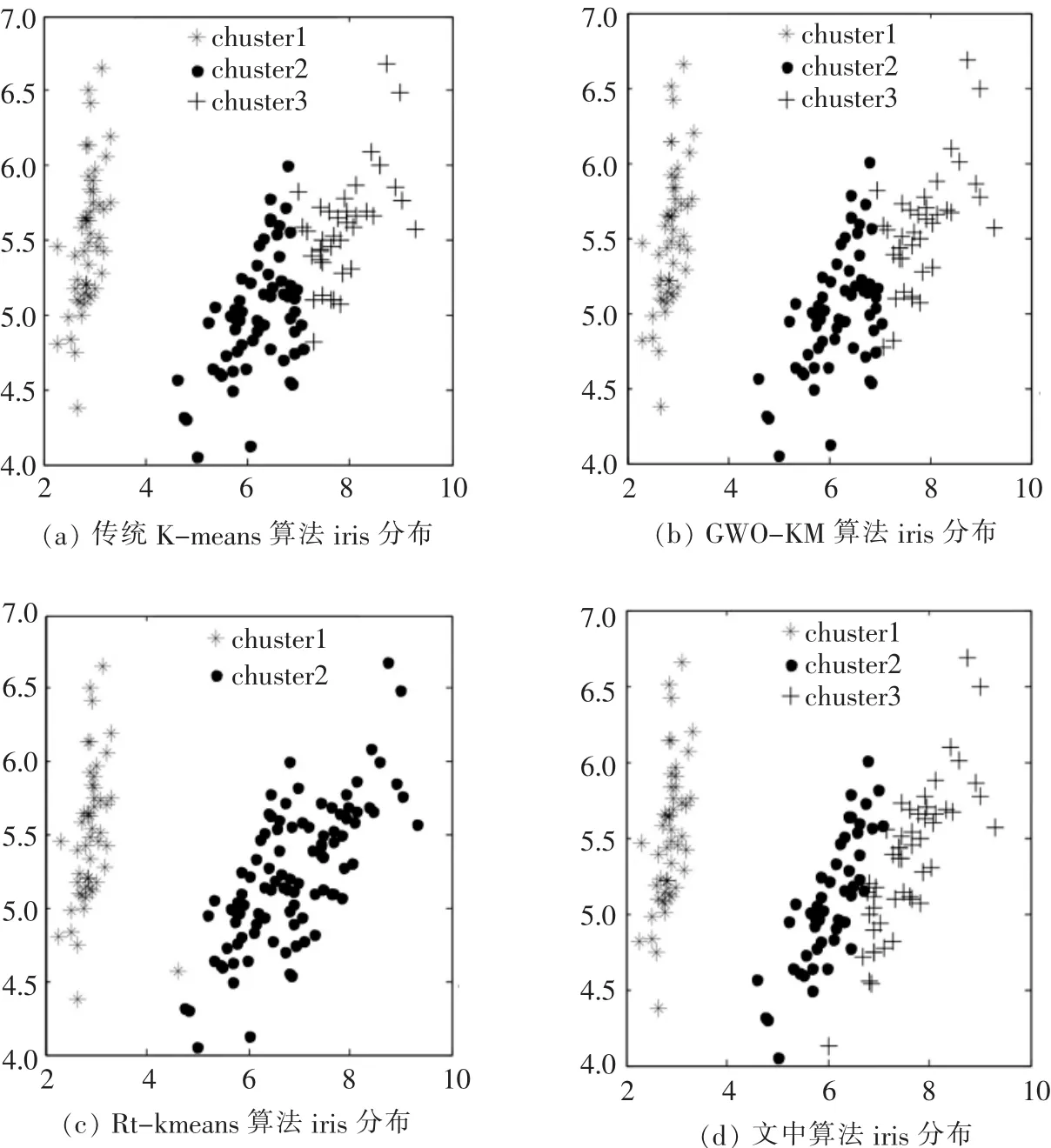
图3 Iris的聚类效果

由表2显示，选取不同的Q值时，将对聚类结果的准确率产生不同的影响.当Q取1时，对于本文所使用的四组UCI数据集，能够得到较好的聚类效果，将Q值增大时，聚类的效果并没有得到改善，甚至导致其聚类的准确率降低，其中对于iris数据集效果尤为明显，当增大Q值时，其准确率非但没有得到改善，反而大幅度的下降．由此证明文中Q取1的合理性及其有效性．

由表3～表6显示，传统K-means算法虽然收敛时间快，但聚类结果是不稳定的，并且聚类的准确率较差．GWO-KM算法相比传统K-means算法虽然聚类的准确率得到一定程度的改善，但相比其它几个算法，其收敛时间很明显耗时较长．Rt-kmeans算法相比传统K-means算法和GWO-KM算法，虽然收敛时间和稳定性都得到较大程度的改善，但对各数据集评价函数的最大值、最小值、平均值所得结果都较差．而文中算法的聚类结果相比其它三个算法，无论是聚类的准确率、评价函数的最大值、最小值、平均值、稳定性及收敛时间都较为优越．

由图2显示，文中的初始化方法与随机初始化和最大最小初始化相比，所得到的初始聚类中心更符合数据集的分布情况，而最大最小初始化所得初始中心绝大部分分布在数据集的边缘．图3是各算法对iris数据的最佳聚类效果图．图 3（a）为传统K-means算法聚类结果，图3（b）为GWO-KM算法聚类结果，图3（c）为Rt-kmeans算法聚类结果，该算法的划分结果仅为两类，其原因是Rt-kmeans算法是一个自动调节聚类中心数目的聚类算法，导致对iris数据集的聚类结果最终类别数与输入数不一致．图3（d）显示，文中算法所获得的数据分布图与原始的数据的分布情况几乎一致，并且对于边界上一些距离较远，但实际相似性较强的对象，通过相关性加权以后能使其聚在相同类中；而对于一些距离相对较近，但实际差异性较大的对象，通过采用加权以后，能使其归为不同的类中，从而增强了相同类中对象间的相关性．通过以上实验结果表明文中算法能有效地提高聚类效果．

4 结束语

文中将皮尔逊相关性系数与传统K-means算法相结合，利用归一化后的相关性系数对传统K-means算法的欧式距离进行加权，从而增强相同类中对象之间的相关性，与传统的K-means算法及其它几种改进的K-means算法相比较，文中算法在聚类的准确率、稳定性、收敛时间等方面都能得到更好的聚类效果．

[1]张宇,朱凝秀．数据挖掘中的模糊聚类分析[J]．工业设计,2012(3):71-72．

[2]张晓慧,孙连山．基于改进K-中心点的电子地图数据质量检查算法[J]．软件导刊,2017,16(2):81-84．

[3]易倩,腾少化,张巍．基于马氏距离的K均值聚类算法的入侵检测[J]．江西师范大学学报,2012,36(5):284-287．

[4]Preeti Arora,Dr．Deepali,Shipra Varshney．Analysis of K-means and K-Medoids alogrithm for big data[J]．Procedia Computer Science,2016,78:507-512．

[5]黄韬,刘胜辉,谭艳娜．基于K-means聚类算法的研究[J]．计算机技术与发展,2011,21(7):54-54．

[6]Kohei Arai,Ali RidhoBarakbah．Hirrarchical K-means:an algorithm for centroids initialization for K-means[J]．Rep．Fac．Sci．Engrg．Saga Univ,2007,36(1):25-31．

[7]Jing Lei，Teng Jiang，Kui Wu．Robust K-means algorithm with automatically splitting and merging cluters and its applications for surveillance data[J]．Multimed Tools Appl,2016,75:12043-12059．

[8]杨红光,刘建生．一种结合灰狼优化和K-均值的混合聚类算法[J]．江西理工大学学报,2015,36(5):85-89．

[9]李振,贾瑞玉．一种改进的K-means蚁群聚类算法[J]．计算机技术与展,2015,25(12):28-31．

[10]洪月华．蜂群K-means聚类算法改进研究[J]．科技通报,2016,32(4):170-173．

[11]张峰,谢振华．基于主成分的改进马氏距离TOPSIS方法[J]．火力与指挥控制,2015,40(3):92-95．

[12]刑涛,黄友红,胡庆荣．基于动态K均值聚类算法的SAR图像分割[J]．中国科学院大学学报,2016,33(5):674-675．

[13]谢娟英,高红超．基于统计相关性的K-means的区分基因子集选择算法[J]．软件学报,2014,25(9):2050-2075．

[14]XiaoyanWang,YanpingBai．TheglobalMinmaxK-means algorithm[J]．SpringerPlus,2016,5:3329-3333．

[15]张良均,杨坦,肖刚．MATLAB数据分析与挖掘实战[M]．北京：机械工业出版社,2016：35-46．