基于TLBO算法优化的球磨机FBEL控制方案研究

杨国亮， 康乐乐, 朱松伟， 许楠

（江西理工大学电气工程与自动化学院，江西 赣州341000）

0 引 言

球磨机作为制粉系统核心设备，在电力、化工、冶金、陶瓷等领域有着不可替代的地位[1].但其难控性、时变性导致工业中常用的PID控制方法很难发挥理想作用，因此，实现球磨机控制的高效自动化是关键问题.随着计算机的高速发展，新的优秀控制理论不断被广大学者提出，如：模糊控制理论、多变量解耦控制理论、机器学习模型控制理论[2].众多新的优秀控制方法也在球磨机控制系统中普遍应用，也获得了令人满意的结果，如：解耦控制、模糊控制、神经网络控制和预测控制等[3].

大脑情感学习模型 （brain emotional learning，BEL）是一种新型的智能机器学习模型，通过模拟人类大脑中情感与学习的机制，从而建立的智能情绪处理功能模型[2,4].近年来，实际控制系统中BEL模型被大量应用.黄国勇等[5]针对无人机飞行姿态控制问题，设计了一种基于BEL模型的混合智能飞行控制系统.文献[6]中，把BEL模型应用在圆锥破碎机控制系统取得理想的控制效果.文献[7]中王帅夫依据步进电动机的对象特性，引入BEL模型，不仅加快了电动机的响应速度，而且有效地抑制了抖动现象.不仅如此，BEL模型在智能洗衣机、直流电机的调速、航天运载火箭控制等实际应用上都取得了很好的效果.

教与学优化算法 （teaching-learning-based optimization，TLBO）是一种新型的智能优化算法，它利用群体的信息进行启发式搜索，通过模拟教师课堂授课和课下学生之间互相学习，以此来提高个体学习成绩，从而提高种群适应度[8]，具有思路简单、收敛快、参数少等特点.文献[9]中何学明将TLBO算法应用在PID控制器的参数寻优中，其参数简单、精度高，收敛快的特性得到了证明.在特征选择问题中，张磊引入教与学优化算法，证明了其具有分类精度高、收敛速度快的特性[10].何红利用教与学优化算法对旅游线路问题进行优化，其具有高效性和实用性[11].李杰等成功应用TLBO算法解决了传统永磁电机参数辨识速度慢、精度低等问题[12].

球磨机控制系统各个参数的精确性，关系到系统能否在最优条件下工作.文中针对此问题将分数阶微积分引入BEL模型，改进普通BEL控制方法，并采用教与学优化算法对球磨机控制系统的各个参数进行优化，得到最佳工作参数，经仿真实验验证球磨机系统的控制效果较好.

1 分数阶BEL模型

1.1 大脑情感学习模型

BEL型在模拟人类大脑中的杏仁体（amygdala）—眶额皮质（orbitofrontal cortex）相互作用的生物学原理，建立的一种新型机器学习模型，简称A-O系统模型[13].于2000年由Moren等人提出，其包括四个部分：丘脑、感官皮质、眶额皮质和杏仁体[14].各部分之间信息传递方式如图1.

图1 大脑情感学习模型

其中，SI表示感官输入信号，由感官输入函数（sensory input function，SIF）计算得出；Rew表示奖励输入信号，由情感暗示函数（emotional cue function，ECF）计算得出.

1.2 分数阶BEL控制器

近年来，分数阶微积分因其对信号与系统的描述更为精准，阶次选择范围更广，动态特性更佳，模型参数个数更少，大大改善了系统性能[15]的优点，受到广大学者和研究人员的关注.基于此，文中将分数阶微积分引入大脑情感学习模型，将误差信号e的分数阶微积分的线性组合作为BEL模型的感官输入信号和奖励信号，构建分数阶BEL（fraction BEL，FBEL）模型，以便提高BEL控制器性能.进而将FBEL模型用于球磨机控制系统，以便提高其控制效果.FBEL控制系统结构框图如图2所示.

图2 FBEL控制系统结构

关于BEL模型研究的重点就是感官输入（Sensory input signal， SI） 信号与奖励信号 （Reward signal，Rew）的选择.根据实际研究需要，SI和 Rew的选取会较高程度影响系统性能．感官输入信号一般为系统的输入与输出、控制量和系统误差等因素组合起来建立的函数关系式，感官输入函数通常为向量形式；而通常将系统误差及其一次微积分形式与控制器输出的线性组合[16]作为奖励信号．

文中依据球磨机系统特性，用信号e作模型输入信号，信号e及其分数阶微积分的线性组合当作BEL模型的SI与Rew信号，使其具有分数阶PID形式．假定μ、λ分别为积分和微分阶次．则文中选择的 SI及 Rew 如式（1）、式（2）：

其中：k1、k2、k3、k4、k5和 k6为权重调节系数．

相比传统BEL模型，文中改进模型可调参数多出两个，从而更加灵活细致高效调整控制器．

2 教与学优化算法

教与学优化 （teaching-learning-based optimization，TLBO）算法是一种新型的智能优化技术，其利用群体信息进行启发式搜索[17]．TLBO算法对优化对象的优化速度快，收敛特性强．它由印度学者R．V．Rao和V．D．Kalyankar于2010年提出，其通过模仿学生在课堂上的学习过程，从而提高各个个体的能力[18]．其中TLBO的种群是整个班级的学员，其中不同的变量就是学员需要学习的不同的课程，计算每个学员的适应度就是考试的过程，学员的考试成绩即为适应度，教师是整个班级体中适应度最好的学员，可以理解为考试成绩最优秀的学员[19]．其定义如下：

TLOB算法的优化过程主要分为两个阶段：教学阶段与学习阶段．教学阶段为学生向教师学习，学习阶段为学生间相互学习，目的都是为了提高成绩（即提高适应度）．其优化过程流程图，如图3所示．

图3 TLBO算法流程

教学阶段：在教学阶段，班级中的各个学员通过全体学员成绩的均值Mean与教师成绩之间的差异difference来向老师学习．学习过程如式（3）、式（4）、式（5）．

其中：ri为随机因子；TFi为教学因子．

由于在班级教学过程中，各个学员学习过程中有很大的随机性，故此教学阶段需要加入教学因子和随机因子．如式（6）、式（7）所示．

自学阶段：TLBO算法依次选中每一个学员，然后随机挑选另外一个学员，通过对比他们之间的差异来完成这一阶段．如式（8）所示．

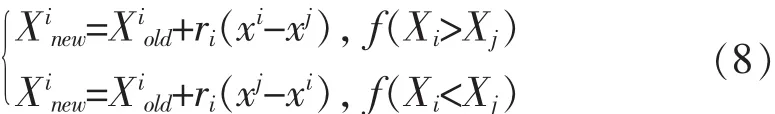
一个班级可表示为以下形式，如式（9）所示．

其中：Xi（i=1，2，…，NP）表示班级学生，NP 为学生个数，d为学生的课程数目．

3 基于TLBO算法的FBEL控制器

FBEL控制器的输入信号包括感官输入信号和情感奖励信号两部分.通常情况下，感官输入信号选取系统输入与输出、控制量及系统误差等，其函数通常采用向量形式；而奖励信号采用适当的系统误差及其积分、微分三者线性函数形式[20].控制器的输入可根据系统特性自由选取，配以权重调节系数对控制器输入信号进行调节.对于感官输入信号和奖励信号的权重调节系数 ki，（i=1，2，3，…，6）以及FBEL的分数阶阶次λ、μ如何整定，目前还未形成系统的理论体系，一般根据系统性能，人工进行调节.人工选取参数具有多种不确定因素，而且参数精度的高低对系统影响较大，其中如何提高参数的精度成为研究的重点.

教与学优化算法利用群体信息进行启发式搜索，其具有优化速度快，收敛性强等特性.文中用TLBO算法对FBEL模型输入函数的权重调节系数ki，（i=1，2，3，…，6）以及分数阶微积分的阶次 λ、μ 进行优化，即 TLBO 算法中的学员/个体 x=[k1，k2，…，k6，λ，μ].

文中将教与学优化算法引入大脑情感学习模型，应用TLBO算法对FBEL控制器的各个参数进行优化，进一步提高参数精度，提高系统的性能.采用加权时间绝对值误差准则 （integral of time-weighted absolute of error，ITAE），作为 TLBO 算法中学员/个体的适应度函数，如式（10）:

基于TLBO优化的球磨机FBEL控制系统模型，如图4所示.

图4 FBEL控制系统模型

4 基于TLBO算法的FBEL球磨机控制原理

球磨机系统是一个复杂系统，且其数学模型不稳定.在实际分析中，通常将此系统作为3输入3输出的控制对象，输入量为：热风量u1、冷风量u2和给料量u3；输出量为：出口温度T、入口负压P和负载量M.其数学模型为：

若对其进行改进，用其轴瓦震动信号来替代负载量.由于冷、热风量不会对其轴瓦信号进行影响，且在实际应用中给料量对入口负压P和出口温度T的影响很小，可直接忽略.因此，可将此3输入3输出的对象分成单输入单输出和2输入2输出两个部分.文中重点研究后者，其数学模型如式（12）：

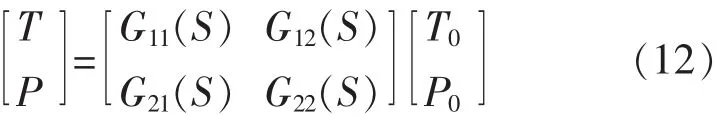
球磨机系统是多变量且有较强耦合的对象，必须要先对它的多个变量进行解耦才能产生较好的控制效果.文中采用多变量逆向解耦控制方法，利用逆向解耦补偿矩阵[20]来构建球磨机控制系统结构.如图5所示.

图5 球磨机的自寻优控制系统结构图

图5 中：T0、P0分别为系统输入；T、P 分别为系统的输出.

整个球磨机控制系统算法流程如下：

I）FBEL连接权值初始化，TLBO学员/个体数量及科目初始化，设定迭代次数；

II）将 xi=[k1，k2，…，k6，λ，μ]依次代入 FBEL 控制器，计算控制器输出；

III）计算逆向解耦补偿模型输出，与FBEL控制器输出之和作为球磨机的控制量；

IV）计算球磨机输出，并计算系统误差；

V）由系统误差通过ITAE函数计算学员/个体适应度Ji；

VI）调用教与学算法优化，开始教学阶段与自学阶段，更新学员/个体参数；

VII）判断是否达到最大迭代次数？否，i=i+1并转 II）；是，转 VIII）；

VIII） 输出最优学员/个体对应的参数 k1，k2，…，k6，λ，μ代入球磨机的FBEL控制系统模型，计算系统输出；

IX）输出T、P，绘制系统阶跃响应曲线.

5 仿真结果与分析

球磨机对象的模型具有时变性，它的数学模型具有随时间而变化的特性，文中使用文献[16]中的两个数学模型对它的动态特性进行模拟仿真实验.2 种工况下，球磨机的数学模型式（13）、式（14）分别为：

为了验证文中教与学优化方法的有效性，文中设计了基于教与学优化算法的FBEL球磨机控制系统模型，然后通过仿真实验验证.文中参考文献[9]设定权重调节系数初始值Ki为零，分数阶阶次μ、λ初始值为0.5，采用绝对误差积分（ITAE）作为评价函数如式（10），同时为了方便比较，同时引入了遗传算法（genetic algorithm,GA）（如图7）和粒子群算法（Particleswarmoptimizationalgorithm,PSO）（如图 8）进行仿真（共20次），各个算法都选取最优的实验结果.文中教与学优化算法如图6所示.

图6 教与学优化曲线

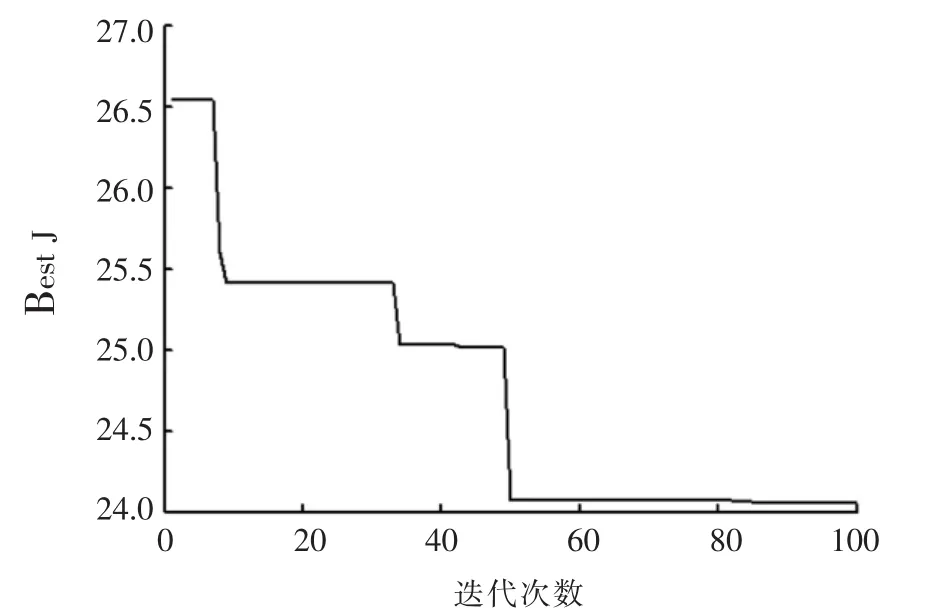
图7 遗传算法优化曲线

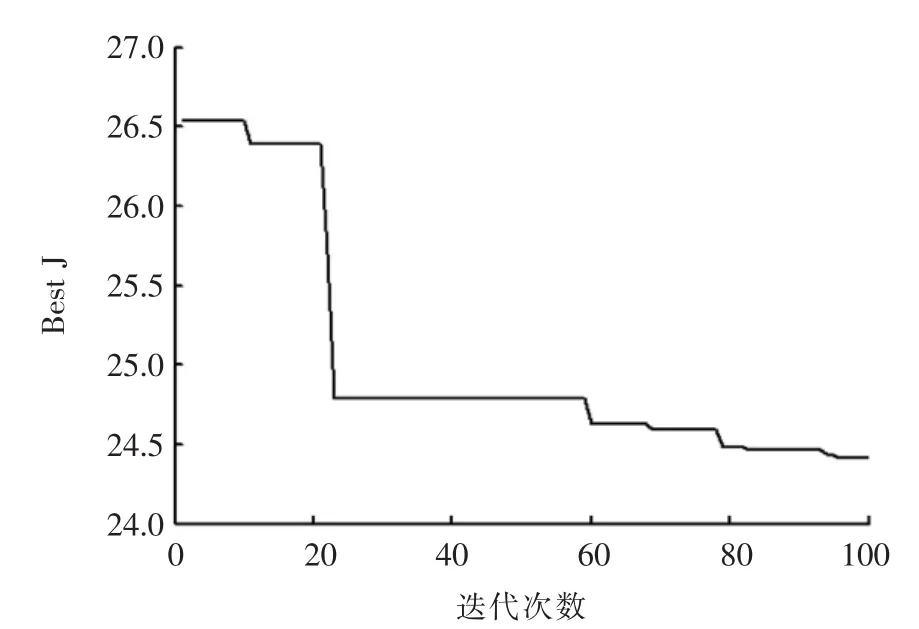
图8 粒子群算法优化曲线

文中对各个算法都进行了100次迭代计算，由图6、图7、图8可以看出文中教与学优化算法在第37次教学时就已经寻到最优解，并且文中TLBO算法收敛性较好，有较好的优化性能，能最快搜寻到最优解.遗传算法在进化到近第50代时找到了最为优秀的解，搜寻速度较文中TLBO方法略慢且易陷入局部陷阱.粒子群算法较文中TLBO方法收敛性较差，出现略微的发散，对文中球磨机系统寻优效果不好.

为了验证文中方法中教与学优化算法对参数优化的精度，将参数代入球磨机模型进行实验.并与未经参数优化、依靠人工经验调整参数的FBEL控制器[16]进行对比，如图9所示.

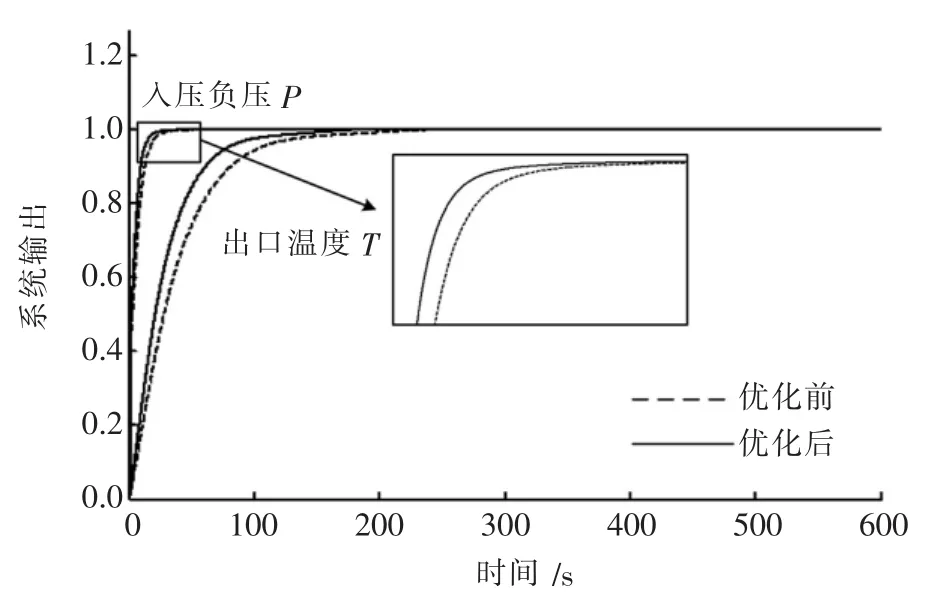
图9 输入[T0P0]=[1 1]的系统阶跃响应曲线

由图9可以看出，当输入为[T0P0]=[1 1]时，FBEL控制方法经过优化后，系统阶跃曲线保持无超调量，调整时间缩短，稳态误差微小，可知文中经教与学优化算法优化后的FBEL控制方法对系统控制更为精细，参数精度较高，提升了球磨机系统控制性能，控制效果较好.

在实际工作中球磨机的数学模型会随工作状况变化而产生一定的变化，为了验证文中优化参数后的控制器对球磨机数学模型的时变不敏感，文中把被控对象数学模型更换为 （工况2，式（14）），与（工况 1，式（13）），比较发现，系统模型的静态增益与时间常数均有10%左右的变化.此时，球磨机系统单位阶跃响应曲线如图10.

图10 输入[T0P0]=[1 1]时系统阶跃响应曲线（工况2）

由图9和图10相同输入情况下的系统阶跃曲线得到，当球磨机数学模型发生小幅度变化时，当文中控制器的对被控对象发生改变时，依然有较好的控制效果，其输出阶跃响应未出现大幅度变化.所以文中经TLBO算法优化的FBEL控制方案对球磨机系统随时间变化的特性依然具有较强的鲁棒性.

球磨机系统在实际运行中，难免会受到或多、或少的外界干扰.为了验证文中控制方法抵抗外部干扰的性能，在系统进入稳定状态后，加入幅值为0.1的干扰信号，如图11所示.由图11可知，文中提出的控制方法的抗干扰性更强.

图11 加入幅值为0.1阶跃干扰信号下的系统抗干扰测试曲线

实际情况中，基于球磨机系统的控制输入信号不稳定性，所以文中引用正弦曲线作为系统的输入信号，以此来验证系统的跟踪特性.

I）当P0是正弦信号，T0=0时，球磨机系统跟踪曲线如12所示，系统跟踪误差曲线如图13所示.由图12和图13可知，文中提出的控制方法对正弦波跟踪误差几乎为0，对入口负压P信号的跟踪发挥不错的效果.

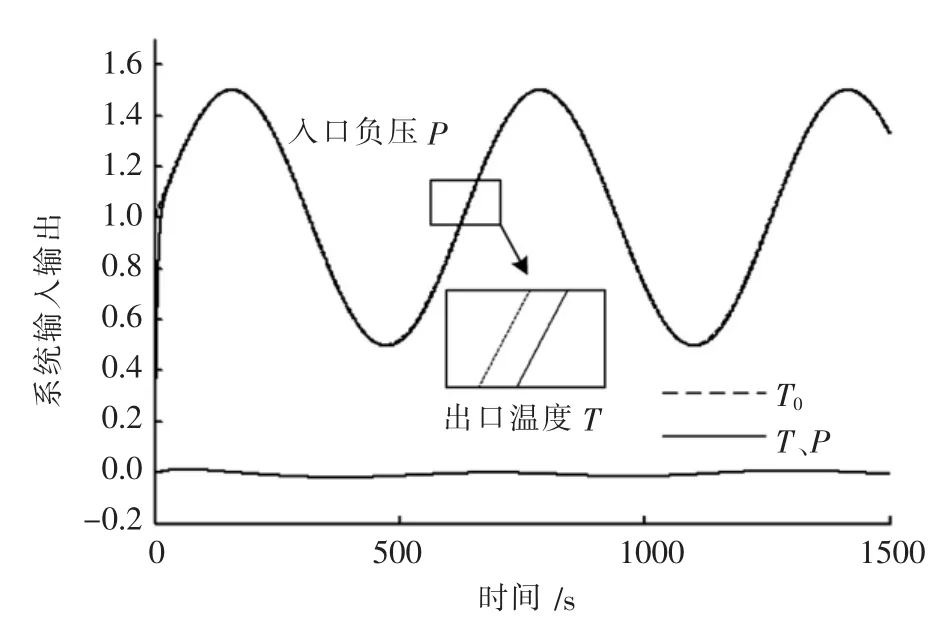
图12 P0为正弦波信号T0=0时系统跟踪曲线

图13 P0为正弦波信号T0=0时系统跟踪误差曲线

II）当T0是正弦信号，P0=0时，球磨机系统跟踪曲线如图14所示，系统跟踪误差曲线如图15所示.由图14和图15可知，文中方法对T0跟踪误差在0附近上下波动，说明对出口温度亦有良好的控制效果.

图14 T0为正弦波信号P0=0时系统跟踪曲线

图15 T0为正弦波信号P0=0时系统跟踪误差曲线

6 结 论

文中针对提高球磨机控制系统的稳定性和控制精度，提出了一种分数阶大脑情感学习模型参数优化方法，采用教与学优化算法优化系统的各个参数.实验结果表明：本方法对参数选取的精确度较高，能更快寻找到最优解，使得系统的各个参数更合理，具有良好的控制性能，提高了球磨机控制系统的精度，表现出良好的鲁棒性.

[1]徐玮,冯晓露,孙坚栋,等.中储式钢球磨煤机制粉系统控制研究[J].热力发电,2014,43(7):87-91.

[2]Cm Lin,Cc Chung.Fuzzy brain emotional learning control system designfornonlinearsystems[J].InternationalJournalofFuzzySystems,2015,10(1):70-75.

[3]任俊超.球磨机系统先进控制算法研究及应用[D].合肥:中国科学技术大学,2015.

[4]Caro Lucas,Danial Shahmirzadi,Nima Sheikholeslami.Introducing belbic brain emotional learning based intelligent controller[J].Intelligent Automation&Soft Computing,2013,1(10):11-21.

[5]黄国勇,甄子洋,王道波.变推力轴线无人机的大脑情感学习智能飞行控制[C]//中国智能自动化会议，2009.

[6]杨国亮,张丽,程智林.基于大脑情感学习模型的圆锥破碎机控制系统研究[J].机械科学与技术,2012,31(1):75-78.

[7]王帅夫,刘景林.基于大脑情感学习模型的步进电机控制系统[J].吉林大学学报(工学版),2014,44(3):765-770.

[8]Shandilya,Pragya.Optimization ofsurface roughnessusing teaching-learning based optimization algorithm and comparison with artificial bee colony algorithm:Department of Mechanical Engineering,Inchon,Korea,2015[C].

[9]何学明,苗燕楠,罗再磊.基于教与学优化算法的pid控制器参数寻优[J].计算机工程,2015,41(8):313-316.

[10]张磊.基于教与学优化算法的特征选择[J].软件导刊,2015,14(11):36-39.

[11]何红,孙根年.基于教与学优化算法的智能旅游线路优化[J].陕西理工学院学报(自然科学版),2015,31(1):72-78.

[12]李杰,王艳,纪志成.基于改进教与学优化算法的永磁同步电机参数辨识[J].系统仿真学报,2017,29(2):393-401.

[13]甄子洋,王道波,王志胜.基于大脑情感学习模型的转台伺服系统设计[J].中国空间科学技术,2009,29(1):13-18.

[14]Naghmeh GARMSIRI,Nariman SEPEHRI.Emotional learning based position control of pneumatic actuators[J].Intelligent Automation and Soft Computing,2014,3(20):433-450.

[15]白珍龙.分数阶模型参考自适应控制的matlab设计[J].工业仪表与自动化装置,2016(1):30-34.

[16]朱松伟.基于分数阶BEL模型的球磨机控制方法研究[D].赣州:江西理工大学,2017.

[17]李志南,南新元,李娜,等.多学习教与学优化算法[J].计算机应用与软件,2016,33(2):246-249.

[18]王培崇.具有自学机制和退火选择的教学优化算法[J].计算机工程与科学,2016,38(4):706-712.

[19]吴宗胜,傅卫平.移动机器人全局路径规划的模拟退火-教与学优化算法[J].机械科学与技术,2016,35(5):678-685.

[20]郑义民,吉国力.一种适合于高阶多变量系统的逆向解耦控制方法[J].北京工业大学学报,2012,38(12):1772-1779.