基于常数矩阵改进的SRC算法

郑俊伟

（四川大学计算机学院，成都 610065）

0 引言

人脸识别技术是近年来被广泛研究的热点之一，人脸识别技术利用从人脸图像提取有效的特征，然后将这些特征信息与数据库中的人脸信息进行搜索比对，从而判断这个人的身份信息。近几年稀疏表示受到越来越多的关注，并且被应用于计算机视觉领域中。尤其是在Wright等人提出的稀疏表示分类方法[1]在人脸识别的应用中取得了很好的识别效果后。稀疏表示分类算法（SRC算法）是近年来新出现的一种人脸识别算法。它的基本思想是给定一个测试样本，然后得到该样本在所有训练样本构成的字典上的稀疏系数，之后利用稀疏系数与训练样本重构测试样本，最后将测试样本分配给重构误差最小的类别。SRC算法可以直接利用原始像素进行人脸识别，从而避免了预处理的过程。除此之外，SRC算法对表情变化、图像遮挡具有一定程度的鲁棒性。但是，在将稀疏表示人脸识别算法应用于实际中，常常需要在两个方面进行改进。首先，是要突破人脸图像对齐的假设，因为在实际环境中人脸的图像是不对齐。但是更重要的是，在实际环境中，常常会发现可用的训练样本非常稀少。为此，大量的学者进行了各种各样的尝试，并提出了许多产生虚拟样本的方案[2-15]。其中一种方案是利用原始训练样本和镜像样本来进行人脸识别。首先利用原始训练样本生成相应的镜像样本。然后将原始训练样本和相应的镜像样本结合产生一个新的训练样本，用于人脸识别。该方法让可用的训练样本数变为原来的两倍。实验结果表明，该方法不仅克服样本稀少的问题，而且克服了人脸图像的不对齐问题，并且在一定程度上消除了人脸图像的姿态变化和光照变化的不利影响。另一种方案是先将人脸分成两个大小相同的两半。然后利用每一半分别产生一张“对称”的虚拟脸。从而让训练样本的数目变成原来的三倍。本文主要针对SRC算法在实际应用中，可用的训练样本少导致识别率低而提出的解决方案。文献[16]提出一种基于多重表示的图像分类新方法，该方法能够为原始训练样本产生新的表示。并且能用图片新的表示提高图像分类的精度。

1 稀疏表示分类算法

SRC算法的基本思想如下[1]：

假设第i类有足够的训练样本，样本图像大小为w×h，第i类有ni个训练样本，把这ni个训练样本数据变 成 列 向 量 ，组 成 矩 阵 Ai, 即 Ai=[υi,1,υi,2,…,υi,n]∈Rm×ni，m=w×h。给定一幅新的第 i类的图像y∈Rm，则y可以由第i类的所有训练样本近似线性表示：

其中，ai,j为标量，j=1,2,…,ni。

由于在识别之前y的类别未知，所以定义一个由所有类别的训练样本组成的矩阵A，假设训练样本有C个类，一共 n个，即则：

如果用A来表示y，那么式（1）可以重写为：

x0=[0,…,0,ai,1,ai,2,…,ai,n,…,0,…,0]T∈ Rm×ni为系数向量，即与第i类对应的系数非零，而其他系数均为零。

在稀疏表示中，通常求解最小化ι1范数问题：

在图像受到小的噪声影响时，上式可以修改为：

其中，ε>0是误差容忍度。

式（5）可以转化为带ι1数约束的最小二乘问题：

其中，λ>0是正则化参数，用来平衡重构误差和稀疏性。当通过求解式（5）或式（6）得到稀疏系数时，基于重构样本和测试样本之间的残差来对测试样本进行分类。对于第i类样本，假设 βi：Rm→Rm为特征函数，它选择与第i类相关的系数，即对于x∈Rm，δi（x）∈Rm是一个新的向量，这个向量中的非零元素对应x中与第i类相关的元素，而对应其它类的系数为0。使用δi()和训练样本组成的矩阵A，可以得到重构样本。然后就可以把测试样本分在最小重构误差对应的类别中：

稀疏表示分类（SRC）算法的流程如下：

（1）输入：由C类训练样本组成的矩阵A=[A1,A2,…,AC] ∈Rm×n，测试样本 y∈Rm（可选参数：容忍误差ε>0）；

（2）将y和A的列向量单位化；

（3）求解（5）或（6）；

输出：测试样本的类别identity(y)=argmiinri(y)。

2 改进的SRC算法

在文献[16]中提出了一种基于多重表示的图像分类新方法。该方法能够为原始训练样本产生新的图像表示。当将图片的新表示与原始训练样本相结合用于图像分类时，能够有效提高图像分类的精度。其定义如下

其中m=255，Iij表示图像I在第i行、第j列的像素的灰度值，而Jij表示图像J在第i行、第j列的像素的灰度值。受到以上模型的启发，本文提出了一种通过使用常数矩阵来获得图像新表示的方法。算法的模型如下：

假设存在C个类，每个类有n个样本，样本图像的大小为w×h。则算法的具体流程如下：

（1）输入：由C个类别的训练样本组成的矩阵A=[A1,A2,…,AC] ∈Rm×n,常量系数 a；

（2）通过常量a与式子（9）计算得到常数矩阵B，其中常数矩阵为w行h列的矩阵；

（3）将常数矩阵B与每个训练样本A（ii=1,2,…,C）相加,获得新的样本，将新样本组成矩阵，其中用表示增强后的样本；

（4）将A与A'整合成一个新的训练样本，然后将其应用于SRC算法中；

（5）输出：测试样本的类别：identity(y)=argmiin ri(y)。

3 实验验证与分析

3.1 改进方法有效性验证

由前面关于SRC算法的介绍可知，SRC算法会将测试样本分到最小重构误差对应的类别。因此，重构误差反映了测试样本与类别的相关程度。即误差越小，相关程度越高。

在这一小节将使用ORL人脸数据库和COIL人脸数据库进行实验，用于验证本文所提出的改进方法能提高算法的识别率。在实验中，取数据库第一个人的某张图片做为测试样本，然后分别使用SRC算法与改进后的SRC算法，计算该图片与数据库中各个人的误差值。图1展现了基于ORL人脸数据库进行实验的结果。图2展现了基于COIL人脸数据库进行实验的结果。

图1 使用ORL人脸数据库进行实验的结果

图2 使用COIL人脸数据库进行实验的结果

3.2 改进方案通用性验证

本小节通过实验来验证本文所提出方法的通用性。在实验中，除了通过SRC算法进行对比实验之外，还使用 CRC 算法[17-20]、LRC 算法[21-24]、CFKNNC 算法[25]和INNC算法[26]进行对比实验。使用的人脸数据库有ORL人脸库、FERET人脸库、AR人脸库和COIL人脸库。

（1）ORL人脸库

ORL是一个基于表情和姿态变化的人脸数据库，该数据库拥有400张人脸图片，它们由40个人，每个人10张不同姿态和表情的人脸图像组成。在实验中，选择每个人的前4张图片作为训练样本，而其余的作为测试样本。这里所选择的常数系数为a=10。图3展现了ORL人脸数据库的部分训练样本与测试样本。表1展现了本文所提方法在不同算法上进行对比实验所得到的识别率。

（2）FERET人脸库

FERET人脸数据库总共拥有1400张人脸图像，包括200个人的数据，由每个人的7张不同光照和姿态的图像构成。在实验中，选择每个人的前4张图片作为训练样本，而将其余的作为测试样本。这里所选择的常数系数为a=10。图4展现了FERET人脸数据库的部分训练样本与测试样本。表2展现了本文所提方法在不同算法上进行对比实验所得到的识别率。

图3 ORL人脸数据库的部分训练样本

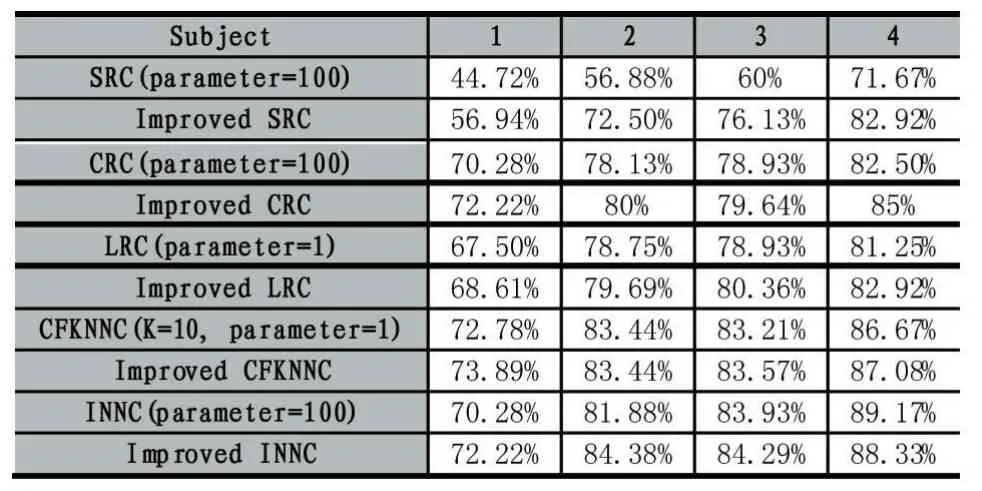
表1 基于ORL人脸数据库的实验结果

图4 基于FERET人脸数据库的部分训练样本

表2 基于FERET人脸数据库的实验结果

（3）AR人脸库

AR人脸数据库拥有超过4000张的人脸图像，包括126个人的数据，由每个人的不同光照、尺度和姿态的图像构成。在实验中，选择每个人的前4张图片作为训练样本，而将其余的作为测试样本。这里所选择的常数系数为a=10。图5展现了AR人脸数据库的部分训练样本与测试样本。表格3展现了本文所提方法在不同算法上进行对比实验所得到的识别率。

图5 基于AR人脸数据库的部分训练样本

表3 基于AR人脸数据库的实验结果

（4）COIL人脸库

本实验所使用的COIL数据库总共包括1440张图像，它由来自20个类别的72张图像组成。在实验中，选择每个人的前4张图片作为训练样本，而将其余的作为测试样本。这里所选择的常数系数为a=10。图6展现了COIL人脸数据库的部分训练样本与测试样本。表4展现了本文所提方法在不同算法上进行对比实验所得到的识别率。

3.3 实验结果分析

1）从图1可以看到SRC算法对测试样本的分类有误，因为最小重构误差出现在第16个类别的位置。但改进后的SRC算法能将测试样本分配到正确的类别。同样的，通过图2可以看到SRC算法对测试样本的分类有误，但改进后的SRC算法则将测试样本分配到正确的类别中。通过以上实验可以发现改进后的SRC算法能减少原本的SRC算法的错误匹配率，从而提高正确识别率。

2）将本文所提出的改进方法应用在除SRC算法以外的算法进行对比实验，可以发现基于本文所提出的方法对其他算法进行改进，也能使其他算法的识别率有所提高，从而证明本文所提出的改进方法具有一定的通用性。

图6 基于COIL数据库的部分训练样本

表4 基于COIL人脸数据库的实验结果

4 结语

本文主要针对SRC算法在实际应用中，可用的训练样本少导致识别率低而提出一种新的方法。该方法通过使用一个特定的常数矩阵与训练样本相加获得新的训练样本，然后将新的训练样本与原始训练样本相结合产生一个新的数据集，从而解决在实际应用中，可用训练样本少而导致识别率低的问题。通过实验表明，该方法不仅能增加可用的训练样本，而且可以提高识别率，除此之外，还证明了该方法具有一定的通用性。

[1]J Wright，AY Yang，A Ganesh，et a1.Robust Face Recognition Via Sparse Representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31(2)：210-227.

[2]Y Xu，X Zhu，Z Li，G Liu，Y Lu and H Liu.Using the Original and‘Symmetricalface’Training Samples to Perform Representation Based two-step Face Recognition.Pattern Recognition，2013，46:1151-1158.

[3]Yong Xu，Zheng Zhang，Guang ming Lu and Jian Yang.Approximately Symmetrical Face Images For Image Preprocessing In Face Recognition and Sparse Representation Based Classification.Pattern Recognition，2016，54:68–82.

[4]Y Xu，X Fang，X Li，J Yang，J You,H Liu，S Teng.Data Uncertainty in Face Recognition.Transactions on Cybernetics，2014，44(10).

[5]P Ekman，J.C.Hager，W.V.Friesen.The Symmetry of Emotional and Deliberate Facial Actions.Psychophysiology，1981，18(2):101-106.

[6]B Tang，S Luo and H Huang.High Performance Face Recognition System by Creating Virtual Sample.In Proc.Int.Conf.Neur.Netw.Signal Process.2003:972-975.

[7]P.Niyogi，F.Girosi，T.Poggio.Incorporating Prior Information in Machine Learning by Creating Virtual Examples.Proc.IEEE.1998，86(11):2196-2209.

[8]D.Jiang，Y.Hu，S.Yan，L.Zhang，H.Zhang，W.Gao.Efficient 3D Reconstruction for Face Recognition.Pattern Recognition，2005，38(6):787-798.

[9]S.N.Kautkar，G.A.Atkinson，M.L.Smith.Face Recognition in 2D and 2.5D Using Ridgelets and Photometric Stereo,Pattern Recognition，2012，45(9):3317-3327.

[10]N.P.H.Thian，S.Marcel，S.Bengio.Improving Face Authentication Using Virtual Samples.IEEE International Conference on Acoustics，Speech，and Signal Processing，2003:6-10.

[11]R Y.-S，O S.-Y.Simple Hybrid Classifier for Face Recognition with Adaptively Generated Virtual Data.Pattern Recognition Letters，2002，23(7):833-841.

[12]T.Vetter.Synthesis of Novel Views from a Single Face Image.International Journal of Computer Vision，1998，28(2):102-116.

[13]X.-T.Yuan，S.Yan.Visual Classification with Multi-Task Joint Sparse Repre-Sentation.IEEE Conference on Computer Vision and Pattern Recognition，2010:3493-3500.

[14]A.Sharma，A.Dubey，P.Tripathi，V.Kumar.Pose Invariant Virtual Classifiers from Single Training Image Using Novel Hybrid-Eigenfaces.Neurocomputing.2010，73(10–12):1868-1880.

[15]Y.Hu，D.Jiang，S.Yan，L.Zhang，H.Zhang.Automatic 3D Reconstruction for Face Recognition，2004:843-850.

[16]Y Xu，B Zhang，Z Zhong.Multiple Representations and Sparse Representation for Image Classification.Pattern Recognition Letters，2015:9-14.

[17]BA Olshausen，DJ Field.Sparse Coding with an Overcomplete Basis Set:a Strategy Employed by V1?Vision Research.1997，37(23):3311.

[18]W.E.Vinje，J.L.Gallant.Sparse Coding and Decorrelation in Primary Visual Cortex During Natural Vision.SCIENCE.2000，287(5456):1273-1276.

[19]M.Elad，M.Aharon.Image Denoising Via Sparse and Redundant Representations Over Learned Dictionaries.IEEE Trans.Image Processing.2006，15(12):3736-3745.

[20]S.H.Gao，I.W-H.Tsang，L-T.Chia.Kernel Sparse Representation for Image Classification and Face Recognition.Proc.European Conf.Computer Vision，2010.

[21]I.Naseem，R.Togneri，M.Bennamoun.Linear Regression for Face Recognition.Transactions on Pattern Analysis and Machine Intelligence.2010，32(11).

[22]P.N.Belhumeur，J.P.Hespanha，D.J.Kriegman.Eigenfaces vs.Fisherfaces:Recognition Using Class Specific Linear Projection.IEEE Trans.Pattern Analysis and Machine Intelligence，1997，19(7):711-720.

[23]R.Barsi，D.Jacobs.Lambertian Reflection and Linear Subspaces.IEEE Trans.Pattern Analysis and Machine Intelligence，2003，25(2):218-233.

[24]X.Chai，S.Shan，X.Chen，W.Gao.Locally Linear Regression for Pose Invariant Face Recognition.IEEE Trans.Image Processing.2007，16(7):1716-1725.

[25]Y.Xu，Q.Zhu，Z.Fan，D.Zhang，J.Mi，Z.Lai.Using the Idea of the Sparse Representation to Perform Coarse-to-Fine Face Recognition.Information Sciences，2013，238:138-148.

[26]Y.Xu，Q.Zhu，Y.Chen J.Pan.An Improvement to the Nearset Neighbor Classifier and Face Recogniton Experiments，2013:543-545.