共因失效条件下多状态系统选择性维修优化
2018-03-15曹文斌贾希胜胡起伟
曹文斌,贾希胜,胡起伟
军械工程学院 装备指挥与管理系,石家庄 050003
在工业和军事领域,装备的动用使用往往由一系列复杂的任务过程组成[1-2],如工业生产线的生产任务、飞机的飞行任务、武器装备的作战或演习任务等。为了确保上述任务的顺利完成,降低故障风险和损失,维修人员往往利用任务间隔时间对装备进行必要的检查和维修。然而,由于可用的装备维修时间、维修费用、维修器材等往往是有限的,有时不可能对所有故障或性能退化部件进行完善维修,而只能选择那些影响下一阶段任务完成的项目实施维修。鉴于此,决策者需要综合考虑任务要求、系统特性、维修需求等因素,科学合理确定最优维修方案。选择性维修理论正是在这种背景下产生的。
选择性维修(Selective Maintenance)于1998年由美国阿肯色大学工业工程系的Rice等[3]首次提出。它是在一定的时间、费用、人员和备件等约束下,通过建立优化目标函数,综合考虑各维修项目的资源消耗情况,从一系列待修项目中优化确定维修项目并形成装备维修方案的过程。自选择性维修提出以来,国内外学者开展了大量相关研究,建立了不同情况下的选择性维修优化模型,如:考虑多种维修方法的选择性维修优化模型[4-7]、考虑多类资源约束的选择性维修优化模型[8]、考虑随机任务的选择性维修优化模型[9-11]、面向装备群的选择性维修优化模型[12]、考虑无限使用期的选择性维修优化模型[13]、考虑维修决策和资源规划的选择性维修优化模型[14]等。近年来,面向多状态系统的选择性维修优化研究受到有关学者的关注,如:Chen等[15]假设任务结束时,部件在各状态的概率可通过一个概率矩阵进行明确定义,建立了面向多状态系统的选择性维修优化模型;Liu和Huang[16]以航空发动机为研究对象,建立了由二态部件组成的多状态系统的选择性维修优化模型;Pandey等[17]研究了由多状态部件组成的多状态系统的选择性维修问题;Dao等[18]研究了存在经济相关性、随机相关性[19]和结构相关性[20]时多状态系统的选择性维修问题,探讨了相关性对选择性维修优化的影响,另外,他们还研究了当多状态系统承受随机负载时的选择性维修优化问题[21]。
在执行任务过程中,由于外部环境(如雷击、辐射、负载、湿度等)的影响,装备的多个组成部件往往会同时发生故障或退化。这种由相同的原因引起的多个部件同时故障或退化的现象称为共因失效(CCF)。通常来说,共因失效可分为确定性共因失效(Deterministic Common Cause Failure)[22]和概率性共因失效(Probabilistic Common Cause Failure)[23-24],这两类共因失效均假设某个共因失效事件的产生是一个确定的概率值。文献[25-26]研究了共因失效事件多次作用对系统可靠性的影响;文献[27]将概率性共因失效进一步扩展为随机共因失效(Random Common Cause Failure, RCCF),即假设共因失效事件的产生服从某一随机分布,且以一定的概率造成不同的部件以不同的概率故障。显然,这类随机共因失效更符合大多数冲击、负载等共因失效事件。
虽然国内外有关学者对面向多状态系统的选择性维修优化和共因失效条件下多状态系统可靠性评估[28-31]进行了有益探讨,但在如下方面还有待开展更为深入的研究:1) 现有的面向多状态系统的选择性维修优化模型未考虑共因失效的影响;2) 评估存在共因失效的多状态系统的可靠性或任务成功概率时,未考虑随机共因失效的情况,即共因失效事件以一定的分布产生,且以一定的概率造成多部件在不同的状态之间转移;3) 大多数文献未考虑系统和任务具有模糊特性的情况。系统和任务参数均为确定值,而工程实践中,由于数据缺乏或工作环境的不确定性,很难得到系统和任务参数的确定值,而只能给出一个模糊的描述,此时,用模糊数表示这些参数更为合理。鉴于此,本文考虑当系统参数(如各部件状态转移率、部件性能等)、任务参数(如任务间隔、任务持续时间、任务需求等)和随机共因失效参数(如共因失效事件达到率、共因失效导致的状态转移概率等)均为模糊数的情况,建立模糊随机共因失效条件下、面向模糊多状态系统的选择性维修优化模型,分析模糊随机共因失效对选择性维修优化和系统模糊状态概率的影响,为科学、合理地维修优化提供模型和理论支撑。
1 问题描述


图1 任务剖面Fig.1 A mission profile

为便于开展研究,这里作以下假设:
1) 每个部件有多种维修方法,不同的维修方法将部件恢复的性能状态不同,且每种维修方法所消耗的时间、费用均已知。
2) 部件的退化由自然退化和随机共因失效两部分造成,二者相互独立,且自然退化符合齐次马尔可夫过程。
3) 维修只能在任务间隔内进行,任务过程中不允许维修。
4) 共因失效事件的产生服从泊松过程。
5) 只有维修方案中所有部件完成维修后,装备才能执行下一个任务。
2 维修方法描述及时间、费用需求建模

1) 不修。不修是指不维修部件,部件的状态保持不变,即mi=Yi。
2) 不完善维修。不完善维修能将部件恢复到介于修复如新和当前状态之间的中间状态,即Yi 3) 完善维修。完善维修是将部件恢复到新部件的状态,即mi=ki。 (1) 图2 维修方法对应的状态转移及时间、费用消耗Fig.2 State transition, maintenance time and cost consumption for each maintenance option (2) (3) (4) (5) (6) 三角模糊数的α(0≤α≤1)水平截集(如图3所示)为 (7) 图3 三角模糊数(a,b,c)的α水平截集Fig.3 α-cut level set of a triangular fuzzy number (a,b,c) 由于部件的退化过程服从马尔可夫过程,且共因失效事件的产生服从泊松过程,因此,考虑随机共因失效事件时,各部件的退化过程仍然可以用马尔可夫过程进行建模。当各参数为模糊数时,基于模糊马尔可夫过程[32],可得到各部件处于各状态的模糊概率。 (8) 图4 由随机共因失效导致部件i的状态转移Fig.4 State transitions of element i due to RCCF 情况1:状态未发生转移 (9) 情况2:由其他状态转移到状态h (10) 综上所述,部件i处在模糊时刻t+Δt处于状态h的概率为 (11) 由式(11)可得 (12) 根据式(12),可写出Kolmogorov微分方程为 (13) (14) (15) 式中:L-1(·)为拉普拉斯反变换运算符。 (16) (17) (18) (19) 在任务结束时,部件i可能处于0到mi的任何一个状态,且处于各状态的概率不同,通过系统中n个部件状态的组合,可以得到任务结束时系统处于各状态的概率及性能。根据FUGF可得到系统在任务结束时的状态分布为 (20) (21) (22) (23) (24) (25) (26) 图5 模糊任务间隔和总维修时间t(L)Fig.5 Fuzzy mission break and total maintenance time t(L) (27) (28) (29) 根据式(23)和式(27),对于维修方案L,模糊多状态系统的模糊任务成功概率为 (30) 根据问题描述,建立选择性维修优化模型的目的是:得到满足费用约束条件下任务成功概率最大时的维修方案;得到最优维修方案对应的维修时间和维修费用;评估最优维修方案的模糊任务成功概率。鉴于此,选择性维修优化模型为 目标函数: max SUα(L) (31) (32) 0≤Yi≤mi≤ki (33) 1≤i≤n (34) 0≤α≤1 (35) 图6 系统结构Fig.6 System structure 表1 各部件状态及模糊性能 表2各部件状态及每种维修方法对应的时间(h)和费用(103元) Table2Elementstatesandmaintenancetime(h)andcost(103yuan)associatedwitheachmaintenanceaction ElementiYisih,jcfixicRicvari,li0,1tfixitRitvari,li0,11011050.221211.2120.22311.2140.31.5401.515100.31.51 表3自然退化导致的各部件模糊状态转移率 Table 3 Fuzzy state transition intensities due to inherent degradation for each element 月-1 表4 随机共因失效导致各部件的模糊状态转移概率 从文中建立的选择性维修优化模型中可以看出,模糊任务成功概率评估是关键。因此,在对选择性模型进行求解之前,首先采用Monte Carlo仿真(Monte Carlo Simulation, MCS)方法,对文中建立的评估随机共因失效条件下多状态系统模糊任务成功概率的解析模型进行验证。由于准确值可以看做模糊数的一种特殊情况,因此,为了简化仿真建模过程,在模型验证时,所有的模糊参数可用准确值代替,但这种简化并不会影响验证结论。建立的仿真流程如图7所示,图中tcur为当前仿真时间;tmin为时间最小值;tc为随机共因失效事件发生时间;state_s为系统状态。具体过程如下: 2) 评估维修方案L的维修时间t(L)和维修费用c(L)。如果t(L)>tb或者c(L)>c0,则执行第10)步。 图7 Monte Carlo仿真流程Fig.7 Procedure of Monte Carlo simulation 3) 根据维修方案L判断部件的当前状态ji,根据系统的结构和各部件状态,判断系统状态state_s,记为: (36) 6) 若td≤tc且td≤tmin,则执行第9)步,否则,执行第7)步; 8) 若tmin 9) 计算系统的性能ps,若ps≥w,则Nsuc=Nsuc+1,跳转至第4)步。 在模型验证之前,需要设置合理的仿真次数值Ntot,若Ntot太小,仿真结果波动较大,可信度不高;若Ntot太大,则仿真时间太长。因此,这里首先分析了仿真结果(任务成功概率)随lg(Ntot)的变化情况,如图8所示。从图8中可以看出,当lg(Ntot)<4.5时,SU(L)对于lg(Ntot)较敏感,浮动范围较大, 很难得到准确的lg(Ntot)值; 当lg(Ntot)≥4.5时,SU(L)的值逐渐趋于稳定,因此在Monte Carlo仿真时,将总仿真次数Ntot设为35 000。 为了便于描述,这里用各部件维修后的状态表示维修方案,即L=(m1,m2,m3,m4)。对于模糊参数(a,b,c)的处理,主要分3种情况:第1种情况(Case 1),所有模糊数取α=0时的下界,即a;第2种情况(Case 2),所有模糊数取α=1时的值,即b;第3种情况(Case 3),所有模糊数取α=0时的上界,即c。在验证时,随机选取了5种不同的维修方案,分别采用文中建立的解析模型(Analytic Model, AM)和Monte Carol仿真法评估了3种情况下的任务成功概率,并计算了二者之差的绝对值(Absolute Value of the Difference, AVD),结果如表5所示。从表5中可以看出,采用文中建立的解析模型和Monte Carlo仿真法得到的任务成功概率值较接近,二者之差的绝对值小于0.1%,在可接受的范围内,证明了文中建立的解析模型的正确性。 图8 仿真次数Ntot对任务成功概率SU(L)的影响Fig.8 Effect of simulation times Ntot on SU(L) 表5 不同维修方案下,解析法和Monte Carlo仿真法的任务成功概率对比Table 5 Comparison of mission success probability obtained by AM and MCS for different maintenance options MaintenanceoptionsL(0,2,1,1)(1,1,1,1)(1,1,1,2)(2,1,1,0)(2,1,1,1)AM00.33260.372000.4195Case1MCS00.33200.371700.4193AVD00.06%0.03%00.02%AM0.44820.18090.20440.37720.4246Case2MCS0.44770.18210.20390.37710.4248AVD0.05%0.02%0.05%0.01%0.02%AM0.39690.53180.55760.35440.5655Case3MCS0.39760.53220.5570.35450.5652AVD0.07%0.04%0.06%0.01%0.03% 由建立的选择性维修优化模型可知,该模型的求解是典型的非线性规划问题。求解这类模型,可采用穷举法和一些智能算法(如遗传算法、粒子群算法等)。由于本文的案例中,可行解的空间并不大,因此,这里采用穷举法求解选择性维修优化模型。 根据各部件的所有可能状态及其维修前的状态,可以得到3×2×2×3=36种可能的维修组合,即维修方案。其中,有些不合理的维修方案可直接排除,如维修方案L=(0,2,2,0),在不维修部件1和部件4的情况下,对部件2和部件3实施完善维修没有实际意义。排除所有不合理的维修方案后,共有12种可行方案,各维修方案的维修时间、费用,模糊任务成功概率如表6所示,其隶属度函数如图9所示。 表6 所有可行方案的模糊任务成功概率,费用(103元)和维修时间(h)Table 6 Fuzzy mission success probability, cost (103 yuan), and maintenance time (h) of all feasible maintenance options 图9 12种维修方案的模糊任务成功概率的隶属度函数Fig.9 Membership functions of the fuzzy mission success probability of system for twelve feasible maintenance options 为了分析随机共因失效对选择性维修优化的影响,这里给出了不考虑随机共因失效时,12种可行方案的模糊任务成功概率的隶属度函数,如图10所示。 图10 不考虑随机共因失效时,12种维修方案的模糊任务成功概率的隶属度函数 Fig.10 Membership functions of fuzzy mission success probability for twelve feasible maintenance options without considering RCCF 从图10中可以看出,当α=1时,维修方案3,即L=(0,2,1,1),为最优维修方案,任务成功概率为0.600 5。此时,最优维修方案与考虑随机共因失效时相同,但是,任务成功概率却远大于0.382 9(图9中方案3);另外,当0≤α<1时,很难从图10中直接选出最优维修方案,但是,可以直观地看出最优维修方案在3、6、7和10中。根据模糊数距离法,求得维修方案3、6、7和10对应的任务成功概率的中心点到原点的距离分别为R3=0.660 3,R6=0.630 5,R7=0.648 8和R10=0.635 6。显然,满足R3>R7>R10>R6,则装备最优维修方案为方案3,即L=(0,2,1,1),与α=1时相同。与4.2节的结果相比可得出,随机共因失效不仅会影响系统任务成功概率,而且可能会影响选择性维修优化结果,因此,在维修优化过程中,需要将任务过程中系统遭受的所有随机共因失效事件考虑在内。 为了进一步分析随机共因失效对系统的影响,这里以维修方案L=(2,1,1,1)为例,分别分析考虑随机共因失效和不考虑随机共因失效条件下,系统在各状态的模糊概率随任务持续时间的变化情况。对于维修方案L=(2,1,1,1)来说,通过分析各部件的状态组合可知,在任务过程中共有3×2×2×2=24种可能的退化状态。根据各状态的系统性能,将其划分为6种性能状态,标记为s1~s6,如表7所示。其中,状态s6的系统性能为0,表示系统故障状态。在任意时刻t,考虑随机共因失效和不考虑随机共因失效时,系统各状态的模糊概率的α=0和α=1的水平截集区间如图11所示。 由于状态s1为系统初始状态,状态s6为系统故障状态,因此,这两个状态的模糊概率能更直观地反映随机共因失效对系统状态的影响。从图11中可看出:随着任务持续时间的增加,系统处于状态s1(即起始状态)的概率逐渐减少,处于状态s6(即故障状态)的概率始终增加,而处于状态s2、s3、s4和s5(即中间状态)的概率先增加后减小,因此,随机共因失效不影响系统各状态概率的变化趋势;考虑随机共因失效时,在状态s1(即起始状态)的概率始终小于不考虑随机共因失效时的概率,而考虑随机共因失效时,系统处于状态s6(即故障状态)的概率始终大于不考虑随机共因失效时的概率,由此可得出,随机共因失效会增加系统故障概率。因此,对随机共因失效进行合理建模,对于准确评估系统状态概率和任务成功概率均具有重要意义。 表7 系统退化状态及性能Table 7 Degraded system states and performance 图11 考虑随机共因失效和不考虑随机共因失效时,系统各状态的模糊概率对比Fig.11 Comparison of fuzzy system state probabilities with and without RCCF 本文考虑多状态系统、任务剖面和随机共因失效的模糊特性,研究了模糊随机共因失效条件下模糊多状态系统的选择性维修优化问题,研究结果表明: 1) 文中建立的模型能有效解决模糊随机共因失效条件下模糊多状态系统的任务成功概率评估和选择性维修优化问题。 2) 模糊随机共因失效和各模糊参数的α水平截集可能会影响选择性维修优化的结果。因此,在选择性维修优化时,需要综合考虑随机共因失效和各模糊参数的α水平截集的影响,否则可能得不到最优维修方案。 3) 虽然模糊随机共因失效不会影响系统各状态概率随任务时间的变化趋势,但是它会显著增加系统故障率,降低系统任务成功概率。因此,为准确评估系统在各状态的模糊概率和系统任务成功概率,在建模时,需要将系统在任务过程中所承受的随机共因失效事件考虑在内,否则,评估结果是不准确的。 [1] PENG R, ZHAI Q Q, XING L D, et al. Reliability of demand-based phased-mission systems subject to fault level coverage[J]. Reliability Engineering and System Safety, 2014, 121: 18-25. [2] PENG R, ZHAI Q Q, XING L D, et al. Reliability analysis and optimal structure of series-parallel phased-mission systems subject to fault-level coverage[J]. IIE Transactions, 2016, 48(8): 736-746. [3] RICE W F, CASSADY C R, NACHLAS J A. Optimal maintenance plans under limited maintenance time[C]∥Proceedings of the Seventh Industrial Engineering Research Conference, 1998. [4] CASSADY C R, POHL E A, MURDOCK W P. Selective maintenance modeling for industrial systems[J]. Journal of Quality in Maintenance Engineering, 2001, 7(2): 104-117. [5] PANDEY M, ZUO M J, MOGHADDASS R, et al. Selective maintenance for binary systems under imperfect repair[J]. Reliability Engineering and System Safety, 2013, 113(1): 42-51. [6] PANDEY M, ZUO M J. Selective maintenance considering two types of failure modes[J]. International Journal of Strategic Engineering Asset Management, 2014, 2(1): 37-62. [7] KHATAB A, AGHEZZAF E H. Selective maintenance optimization when quality of imperfect maintenance actions are stochastic[J]. Reliability Engineering and System Safety, 2016, 150: 182-189. [8] CAO W B, JIA X S, HU Q W, et al. Selective maintenance for maximising system availability: A simulation approach[J]. International Journal of Innovative Computing and Applications, 2017, 8(1): 12-20. [9] CAO W B, HU Q W, SONG W Y, et al. Mission-oriented maintenance optimization subject to resources constraints[C]∥International Conference on Intelligent Networking and Collaborative Systems. Piscataway, NJ: IEEE Press, 2016: 237-243. [10] KHATAB A, AGHEZZAF E H, DJELLOUL I, et al. Selective maintenance optimization for systems operating missions and scheduled breaks with stochastic durations[J]. Journal of Manufacturing Systems, 2017, 43: 168-177. [11] KHATAB A, AGHEZZAF E H, DIALLLO C, et al. Selective maintenance optimization for series-parallel systems undergoing alternating missions and scheduled breaks with stochastic durations[J]. International Journal of Production Research, 2017, 55(10): 3008-3024. [12] SCHNEIDER K, CASSADY C R. Evaluation and comparison of alternative fleet-level selective maintenance models[J]. Reliability Engineering and System Safety, 2015, 134: 178-187. [13] MAILLART L M, CASSADY C R, RAINWATER C, et al. Selective maintenance decision-making over extended planning horizons[J]. IEEE Transactions on Reliability, 2009, 58(3): 462-469. [14] SHARMA P, KULKARNI M S, YADAV V. A simulation based optimization approach for spare parts forecasting and selective maintenance[J]. Reliability Engineering and System Safety, 2017, 168: 274-289. [15] CHEN C, MENG M Q H, ZUO M J. Selective maintenance optimization for multi-state systems[C]∥Proceedings of the 1999 IEEE Canadian Conference on Electrical and Computer Engineering. Piscataway, NJ: IEEE Press, 1999, 3(3): 1477-1482. [16] LIU Y, HUANG H Z. Optimal selective maintenance for multi-state systems under imperfect maintenance[J]. IEEE Transactions on Reliability, 2010, 59(2): 356-367. [17] PANDEY M, ZUO M J, MOGHADDASS R. Selective maintenance modeling for a multistate system with multistate components under imperfect maintenance[J]. IIE Transactions, 2013, 45(11): 1221-1234. [18] DAO C D, ZUO M J, PANDEY M. Selective maintenance for multi-state series-parallel systems under economic dependence[J]. Reliability Engineering and System Safety, 2014, 121(1): 240-249. [19] DAO C D, ZUO M J. Selective maintenance for multistate series systems withs-dependent components[J]. IEEE Transactions on Reliability, 2015, 99: 1-15. [20] DAO C D, ZUO M J. Selective maintenance of multi-state systems with structural dependence[J]. Reliability Engineering and System Safety, 2017, 159: 184-195. [21] DAO C D, ZUO M J. Optimal selective maintenance for multi-state systems in variable loading conditions[J]. Reliability Engineering and System Safety, 2017. http:∥www.sciencedirect.com/science/article/pii/S0951832016308213. [22] XING L D, LEVITIN G. BDD-based reliability evaluation of phased-mission systems with internal/external common-cause failures[J]. Reliability Engineering and System Safety, 2013, 112: 145-153. [23] XING L D, BODDU P, SUN Y L, et al. Reliability analysis of static and dynamic fault-tolerant systems subject to probabilistic common-cause failures[J]. Proceeds of the Institution of Mechanical Engineers Part O: Journal of Risk and Reliability, 2010, 224(1): 43-53. [24] WANG C N, XING L D, LEVITIN G. Explicit and implicit methods for probabilistic common-cause failure analysis[J]. Reliability Engineering and System Safety, 2014, 131: 175-184. [25] 王正, 谢里阳, 张君一. 载荷多次作用下的共因失效系统可靠性模型[J]. 航空学报, 2007, 28(s1): s116-s120. WANG Z, XIE L Y, ZHANG J Y. Reliability model of system with common cause failure under repeated random load[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(s1): s116-s120 (in Chinese). [26] 高鹏, 谢里阳. 基于改进发生函数方法的多状态系统可靠性分析[J]. 航空学报, 2010, 31(5): 934-939. GAO P, XIE L Y. Reliability analysis of multi-state systems based on improved universal generating function[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 934-939 (in Chinese). [27] 曹文斌, 胡起伟, 苏续军, 等. 随机共因失效条件下的多阶段任务成功概率评估研究[J]. 兵工学报, 2017, 38(4): 766-775. CAO W B, HU Q W, SU X J, et al. Research on phased-mission success probability assessment under random common cause failures[J]. Acta Armamentarii, 2017, 38(4): 766-775 (in Chinese). [28] LEVITIN G. Incorporating common-cause failures into norepairable multistate series-parallel system analysis[J]. IEEE Transactions on Reliability, 2001, 50(4): 380-388. [29] LI C Y, CHEN X, YI X S, et al. Heterogeneous redundancy optimization for multi-state series-parallel systems subject to common cause failures[J]. Reliability Engineering and System Safety, 2010, 95: 202-207. [30] MI J H, LI Y F, HUANG H Z, et al. Reliability analysis of multi-state system with common cause failure based on bayesian networks[J]. Maintenance and Reliability, 2013, 15(2): 169-175. [31] MI J H, LI Y F, LIU Y, et al. Multi-state systems under epistemic uncertainty and common cause failures[J]. IEEE Transactions on Reliability, 2015, 64(4): 1300-1309. [32] LIU Y, HUANG H Z, LEVITIN G. Reliability and performance assessment for fuzzy multi-state elements[J]. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 2008, 222(4): 675-686. [33] LIU Y, HUANG H Z. Reliability assessment for fuzzy multi-state systems[J]. International Journal of Systems Science, 2010, 41(4): 365-379. [34] DING Y, LISNIANSKI A. Fuzzy universal generating functions for multi-state system reliability assessment[J]. Fuzzy Sets and Systems, 2008, 159(3): 307-324. [35] CHENG C H. A new approach for ranking fuzzy numbers by distance method[J]. Fuzzy Sets and Systems, 1998, 95: 307-317.



3 模糊随机共因失效条件下模糊多状态系统选择性维修优化建模
3.1 模糊集和模糊数


3.2 基于模糊马尔可夫过程和模糊通用生成函数的模糊多状态部件状态分布










3.3 基于模糊通用生成函数的模糊多状态系统状态分布

3.4 模糊多状态系统模糊任务成功概率评估





3.5 选择性维修优化建模

4 案例分析






4.1 模型验证








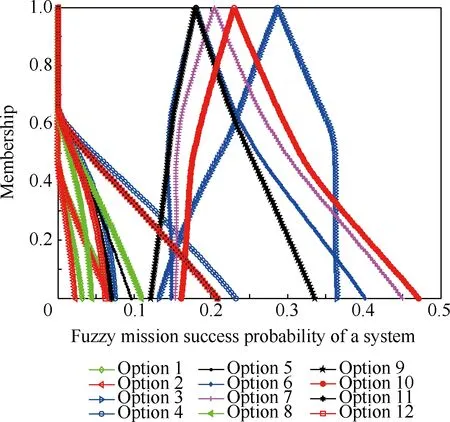
4.2 选择性维修优化结果


4.3 随机共因失效对选择性维修优化的影响

4.4 随机共因失效对系统各状态的模糊概率的影响


5 结 论
