圆盘结构下旋转爆震波的不稳定传播特性
2018-03-15夏镇娟马虎卓长飞周长省
夏镇娟,马虎,卓长飞,周长省
南京理工大学 机械工程学院,南京 210094
爆震波是一种超声速燃烧波,是激波与火焰面紧密耦合的联合体,气流跨过它后热力学状态(如压力、温度等)会急剧增加。爆震燃烧接近于等容燃烧,具有能量释放率快、热力循环效率高等优点,与等压燃烧相比,基于爆震燃烧的推进系统具有更高的热效率,在航空航天领域有广阔的应用前景。
旋转爆震发动机(Rotating Detonation Engine,RDE)是基于爆震燃烧的一种新型动力推进装置,一道或多道旋转爆震波(Rotating Detonation Wave, RDW)在燃烧室内连续传播,爆震产物从另一端排出并产生连续推力。RDE的燃烧室构型主要有3种形式:同轴圆环形、无内柱圆筒形以及圆盘形结构。目前实验及数值模拟的研究工作主要集中在同轴圆环形结构,针对另外两种结构也有部分研究。
20世纪60年代,Voitsekhovskii等[1]在圆盘形发动机上首次进行了旋转爆震的实验研究,得到了连续传播的旋转爆震波,并使用转鼓式相机拍摄到旋转爆震波的流场结构,开创了RDE实验研究的先河。之后,众多国家和机构[1]也相继开展了大量的实验及数值研究。实验方面,Bykovskii等[2-3]实现了多种气态及液态燃料的旋转爆震燃烧,并采用速度补偿法记录了旋转爆震波的传播过程,发现了两种不同结构的同向传播模态,以及爆震波的对撞传播和轴向脉冲传播模态。Anand等[4-5]进行了H2/Air在环形燃烧室内的实验研究,通过改变反应物的质量流率及发动机的尺寸,得到了4种不稳定传播模态:非周期性无序传播模态(重复熄灭、再起爆过程)、低频正弦振荡模态、多波转变模态以及轴向脉冲传播模态。Rankin等[6]使用OH*化学发光技术进行RDE的可视化实验研究,观测到燃烧室中爆震波的形状和尺寸、其后的斜激波,以及新鲜填充气体与燃烧产物之间的缓燃面等。Zhang等[7]在无内柱空心圆筒燃烧室中进行了H2/Air旋转爆震的实验研究,得到了不同Laval喷管收缩比下爆震波的传播模态,并与切向不稳定燃烧模态进行了对比。数值模拟方面,国内外学者进行了大量的二维及三维数值研究,得到了旋转爆震波的精细波系结构及自持机理[8-9],Manabu等[10]揭示了旋转爆震波“燃烧波+激波”的组合特性。Eude等[11]模拟了增加环形燃烧室宽度后的三维流场结构,发现当宽度变大后,燃烧室径向尺寸的影响会越来越明显,且在燃烧室径向也观察到了清晰的横向爆震波结构。Frolov等[12]开展了考虑黏性和推进剂分开喷注的三维数值模拟,发现了燃烧室中多个强度不同的爆震波头,与实验结果吻合。Tang等[13]对无内柱的圆筒形发动机进行了三维数值模拟,得到了稳定传播的多波头旋转爆震波。Li等[14]数值研究了弯管中爆震波的传播特性,得到了两种传播模态:一种为解耦—再起爆模态,随着曲率半径的减小,靠近内圆附近的爆震波发生解耦,流场中的横波传播到内圆附近,重新起爆爆震波;另一种为曲率半径增大到一定值后,爆震波以稳定模态传播。
Bykovskii等[15]在圆盘形发动机上进行了煤粉/空气的两相爆震实验研究,实验成功起爆并得到了脉冲爆震波和旋转爆震波,并采用侧壁面开窗的方式成功观察到流场内的爆震波结构。Nakagami等[16]设计了两侧(或单侧)为石英玻璃壁面的圆盘形发动机,通过高速摄影及纹影技术观测燃烧室全流场结构,便于研究爆震波的传播特性。Ishiyama等[17-18]将这种圆盘形发动机与涡轮及压气机组合,设计了旋转爆震涡轮组合发动机,并进行了冷流及燃烧实验。可视化实验的圆盘形RDE燃烧室示意图如图1所示,燃料与氧化剂从燃烧室外圆喷注进入燃烧室,产物从内圆喷出,流道收敛,流通面积渐缩,这与传统的圆环形燃烧室的等直通道有所差异。

图1 可视化实验的燃烧室示意图[16]Fig.1 Diagram of combustor used in visualization experiment[16]
基于上述研究背景,忽略圆盘形燃烧室宽度的影响及出口流动的相互作用,将燃烧室简化为二维环形收敛模型,喷注入口为计算域外圆,出口为计算域内圆。由于计算域为渐缩通道,不同于传统的RDE沿母线展开的二维矩形计算域,旋转爆震波的传播特性必然有所不同,有必要进行相关研究工作。本文开展了二维环形计算域的数值研究,得到两种典型的旋转爆震波传播模态,并对旋转爆震波的不同传播模态进行对比分析,重点研究不稳定传播模态的流场特征,以及爆震波参数、出口流场参数和出口增压比的变化规律。
1 数值方法
1.1 求解方法
针对2H2+O2+3.76N2的反应混合物,本文进行二维圆盘结构下旋转爆震波传播特性的数值模拟。忽略黏性、热传导和扩散等输运效应,采用有限体积法离散二维化学非平衡流Euler控制方程组,采用重构-推进方法计算无黏通量,对流项采用Steger-Warming矢通量分裂格式进行离散,使用时间算子分裂算法处理化学非平衡流中的刚性问题,化学反应机理采用7组分8步基元反应,采用有限速率化学反应模型,使用Arrhenius公式计算反应速率常数。本文所用数值方法的详细介绍及其验证见文献[19-20],这里不再赘述。
1.2 计算模型与边界条件
本文所用计算模型为二维环形收敛计算域,如图2所示,其中,Dout为计算域外径,Din为计算域内径。

图2 二维环形计算域Fig.2 Two-dimensional annular computational domain
计算域外圆边界为喷注入口边界,边界上网格单元的流动情况由该处的压力p决定,内圆边界为出口边界。入口边界条件为
1)p≥p0,p0为预混气体的喷注总压,流动处于阻塞状态,喷注速度为0,预混气体不能有效喷注进入燃烧室。
2)p0>p>pcr,喷注速度按等熵膨胀公式计算:
(1)
式中:T0=300 K为喷注总温;γ为反应混合物的比热比;R为混合物的气体常数。pcr为临界喷注压力,其表达式为
(2)
3)p≤pcr,流动处于壅塞状态,喷注速度为
(3)
计算域的出口边界为
1) 出口为超声速,所有守恒变量由内部流场外推得到。
2) 出口为亚声速,边界处压力等于外界反压,其他守恒变量由内部流场参数外推得到,本文算例的外界反压皆为0.1 MPa。
点火区域为一扇形高温高压区域,如图2所示,点火区压力为2.5 MPa,温度为3 000 K。预混气体采用分段填充[21]的方式,第1个循环周期内,在点火段左侧的扇形区域(如图2所示)填充惰性气体(N2),其他区域按入口边界条件填充可燃预混气体,以保证形成沿一个方向传播的旋转爆震波。
本文的计算旨在研究二维环形计算域内旋转爆震波的不稳定传播特性及其参数的变化规律,不考虑旋转爆震波的精细结构,综合计算资源的限制,最终选择1/3 mm的网格尺度为计算尺寸。网格无关性验证已在之前的研究工作中完成[22]。
2 结果与讨论
通过改变二维环形计算域的几何尺寸,本文进行了圆盘结构下的二维数值模拟工作,得到了旋转爆震波的两种典型传播模态:稳定传播模态和不稳定传播模态。其中,稳定传播模态在之前的研究工作中已进行了详细的研究及分析[22],在此不再赘述,仅作为对比参考。本文着重研究不稳定传播模态下旋转爆震波的流场特征、爆震波参数变化等。初步研究发现,环形计算域的曲率半径、宽度(B)以及喷注总压对旋转爆震波的传播模态都有影响,计算工况及结果如表1所示。本文将选取典型工况2进行详细分析。
由之前的研究可得,工况1下,旋转爆震波在二维环形计算域内以稳定模态传播,传播过程中,旋转爆震波的波系结构及爆震波强度皆能达到相对稳定的状态,如图3所示,其中t为计算时间。在本文中,工况1仅仅作为对照工况,而不再进行详细分析。

表1 计算工况及结果Table 1 Calculation cases and results
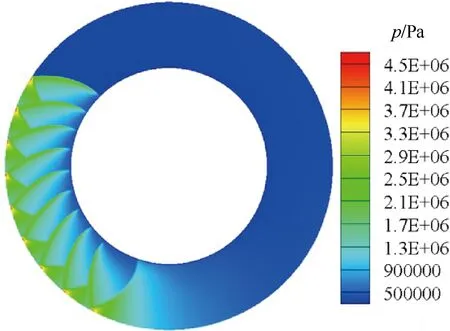
图3 RDW稳定传播模态的流场压力云图 (工况1,t:1.258~1.295 ms)Fig.3 Contours of pressure of RDW flow field in stable propagation mode (Case 1,t: 1.258-1.295 ms)
与工况1相比,工况2中保持计算域的曲率半径(内圆半径)不变,减小计算域的宽度。旋转爆震波仍能成功起爆并沿周向传播,但传播过程并不稳定,在传播过程中重复出现“解耦—再起爆”的现象,下面将对这种不稳定传播模态进行详细分析。
2.1 不稳定传播流场云图
工况2下,旋转爆震波起爆成功,但爆震波在传播过程中出现了“解耦—再起爆”的现象。图4、图5为不稳定传播模态下不同时刻的流场云图,图4表示旋转爆震波解耦的过程,图5为爆震波重新起爆的过程,其中图4(a)、图5(a)为压力云图,图4(b)、图5(b)为温度(T)云图,图4(c)为某一时刻H2质量分数(CH2)的局部放大图,图5 中HS(Hot Spot)为局部热点。图6为不同时刻压力云图的局部放大图,图中:DW(Detonation Wave)为爆震波,RW(Reflected Wave)为反射激波,DLW(Decoupling Leading shock Wave)为解耦前导激波,TDW(Transverse Detonation Wave)为横向爆震波。
由图4可得,旋转爆震波在二维环形计算域内传播时,靠近内圆出口位置,爆震波的前导激波与火焰锋面逐渐发生分离,这主要是由于内圆附近扩张几何曲面的发散作用削弱了爆震波的强度,当燃烧产生的能量不能维持前导激波的传播时,火焰锋面与前导激波面逐渐分离,爆震波发生解耦。由温度分布图4(b)可得,工况2在图4中的解耦开始时刻约为0.243 ms,且靠近出口的解耦区域会逐渐往流场内部扩散,影响环形流场内爆震波的传播,但爆震波的解耦范围是有限的,在该计算工况下,最大解耦区域的径向尺寸占整个环形计算域宽度的2/3左右。图4(c)为t=0.257 5 ms时刻H2质量分数云图的局部放大图,由图4(b)、图4(c)可以看出,在爆震波解耦区域,前导激波与其后的火焰锋面之间存在一小块未燃气体区域(Unburned Zone,UZ)。

图4 RDW不稳定传播模态的流场云图(解耦,工况2,t:0.233 33~0.262 49 ms)Fig.4 Contours of RDW flow field in unstable propagation mode (decoupling,Case 2,t: 0.233 33-0.262 49 ms)

图5 RDW不稳定传播模态的流场云图(再起爆,工况2,t:0.265 66~0.308 87 ms)Fig.5 Contours of RDW flow field in unstable propagation mode (re-initiation,Case 2,t: 0.265 66-0.308 87 ms)
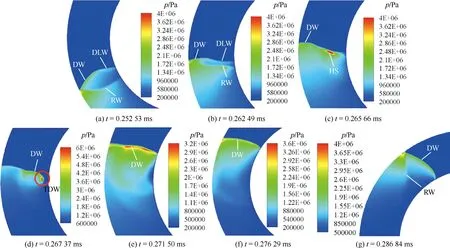
图6 不同时刻压力云图的局部放大图Fig.6 Detail views of pressure contours at different moments
由图4(a)的压力云图可得,旋转爆震波解耦之前,前导激波与其在外壁面的反射激波之间的夹角较大且维持在一定值范围之内,这与稳定传播工况的压力流场云图一致,如图3所示。但随着出口附近爆震波的解耦,解耦处前导激波的传播速度降低,逐渐落后于未解耦区,而爆震波的解耦对反射激波的传播影响较小,反射激波的传播速度变化不大。因此,随着时间的推移,前导激波与反射激波的夹角逐渐变小,两者距离缩短,如图6(a)所示,到图4(a)压力云图的最后一个时刻,反射激波有赶上前导激波的趋势,图6(b)为该时刻压力云图的放大图,由图6(b)可得,爆震波的解耦区域约占整个环域宽度的2/3,反射激波受解耦区域的影响,波形发生变化,但传播速度仍比解耦的前导激波快,有追赶上前导激波的趋势。
结合图4及图6(b)的分析,前导激波与反射激波的距离逐渐缩短,最终反射激波赶上前导激波,两道激波发生碰撞,如图6(c)所示,碰撞点处的压力、温度骤然上升,远高于流场其他位置,流场中出现局部热点HS。局部热点在未燃预混气体中以半圆形波阵面快速膨胀传播,如图6(d)所示。由图4(b)、图4(c)可知,由于爆震波的解耦,流场出口附近存在一小块未燃区域,重新起爆的半圆形爆震波在流场中传播时,遇到该未燃气体区域并迅速形成了一道沿径向传播的横向爆震波TDW,如图6(d)中实线圆圈所示。由于该区域的未燃气体经过前导激波压缩,初始压力较高,因此,在该区域形成的沿径向传播的爆震波的强度远高于沿周向传播的旋转爆震波。
经过约5.8 μs,局部热点形成的半圆形爆震波扩展到环形区域的整个径向,在流场中形成了近似的平面爆震波,如图6(e)、图6(f)所示,右侧的横向爆震波传播至内圆附近时,由于内圆边界为出口无反射边界条件,TDW直接传出计算域而未发生反射。平面爆震波沿环形计算域传播一段时间后,由于计算域几何条件的影响,逐渐恢复成解耦之前的曲面爆震波形状,其波后同样形成了反射激波,如图6(g)所示,这与解耦之前的流场极为相似。但重新起爆的爆震波并没有稳定传播下去,而是在接下来旋转爆震波沿周向传播的整个过程中(该算例下旋转爆震波传播了12个周期)一直重复循环“解耦—再起爆”的过程,这由图5后面时刻的流场图可以看出,重新起爆的爆震波刚恢复解耦前的波形,在靠近出口区域又出现了解耦现象。
2.2 流场参数变化
为对比研究旋转爆震波在不稳定传播模态与稳定传播模态下流场参数的差异,该节研究了不同径向位置处旋转爆震波的压力、温度、传播速度等的变化,并与同一初始条件下的理论值进行对比,分析爆震波的不稳定传播对爆震参数的影响。
2.2.1 爆震波压力
由之前的研究工作可得,在稳定传播模态下,爆震波流场内各监测点处的压力值呈现周期性变化趋势,且压力峰值相对稳定。而对于不稳定传播模态,流场内的压力变化与爆震波的解耦再起爆时刻及位置有关,图7对比研究了两种传播模态下不同径向位置处压力随时间的变化情况,其中各监测点的布置如图2所示,D为不同监测点处的直径。
由图7(a)可得,稳定传播模态下,同一监测点处各周期之间旋转爆震波的峰值压力差别很小,说明爆震波在该工况下能实现稳定传播,但不同径向位置的爆震波压力值不同,这主要是由环形计算域的几何条件所致,外圆壁面的收敛汇聚作用增强了爆震波强度,而内圆出口附近的发散作用削弱了爆震波强度,使得越靠近内圆出口,爆震波的强度及峰值压力越小。
由图7(b)可得,不稳定传播模态下,旋转爆震波不仅在不同径向位置处压力峰值不同,而且在同一监测点的不同传播周期内,爆震波的峰值压力也存在较大差异,且越靠近计算域的出口,这种差异越大。这说明在工况2条件下,旋转爆震波强度随时间呈现强弱变化规律。这与2.1节的压力流场云图相对应,不稳定传播模态下旋转爆震波重复出现“解耦—再起爆”的循环过程。如图7(b)所示,虚线圆圈所示即为爆震波发生解耦时的压力峰值,由于解耦的前导激波缺少化学反应能量的支持,激波强度下降,压力随之下降。而其后一个压力峰值却远大于流场中其他位置处的压力,如图中实线圆圈所示,说明此时流场中存在局部热点形成的过驱爆震波,之后过驱爆震波逐渐衰减为旋转爆震波。由图中还可以发现,越靠近外圆,不同周期的压力峰值差异越小,这也与压力云图相对应,靠近外圆的爆震波强度较高,足以抵抗稀疏波的削弱,并未发生解耦,但仍然受到解耦部分流场的影响,爆震波压力有小幅度波动。

图7 不同直径处压力随时间的变化Fig.7 Variation of pressure with time in different diameters
2.2.2 周向压力、温度分布
为研究爆震波解耦和重新起爆时流场内压力、温度等参数的变化情况,提取同一径向位置、不同时刻的周向数据,对比不同时刻流场中压力、温度的周向分布,详细分析不稳定传播模态下爆震波解耦以及再起爆的过程。
由前面的流场云图分析已得,工况2条件下爆震波的解耦区域约占环形计算域宽度的2/3,因此,选取直径70 mm处监测点的周向数据来研究爆震波的解耦—再起爆过程。

图8 不同时刻的压力、温度曲线(监测点:D=70 mm)Fig.8 Pressure and temperature curves at different moments (monitoring point: D=70 mm)
图8选取了3个不同时刻周向的压力、温度数据,分别对应于爆震波未解耦、解耦以及再起爆阶段。
由图8(a)可知,爆震波解耦前,前导激波与燃烧波紧密耦合,爆震波的压力峰值为2.12 MPa,温度峰值为2 171 K,用CEA(Chemical Equilibrium with Applications)计算理论压力值为2.01 MPa,温度为2 920.6 K,爆震速度为1 975.6 m/s。其中,计算初始条件取波前的压力和温度值(分别为82.782 kPa和190.65 K)。计算压力值与理论值吻合较好,但温度相差较大,这可能受计算域曲率的影响。图8(b)为爆震波解耦时刻的曲线图,从图8(b)及其局部放大图可得,温度曲线上升的周向位置明显落后于压力曲线,说明此时的前导激波与燃烧波已经分离,爆震波解耦,且该时刻下的压力峰值仅为0.92 MPa,远低于CEA理论计算值,另一个波峰代表反射激波,由曲线图可得,反射激波的压力峰值要高于解耦的前导激波,说明反射激波受爆震波解耦的影响较小,此时反射激波的强度高于解耦后的前导激波强度,这也为反射激波追赶上前导激波,重新起始爆震波提供条件。图8(c)表示压力和温度的上升位置吻合良好,说明前导激波与火焰锋面重新耦合在一起,且由图8(c)可得,此时的压力峰值高达3.50 MPa,高于理论计算值,这说明此处为局部热点形成的过驱爆震波,过驱爆震波逐渐衰减后形成旋转爆震波。
2.2.3 传播速度
图9表示工况2条件下,爆震波解耦过程中,不同径向位置处前导激波(Leading Shock wave, LS)及反射激波RW的传播速度随时间的变化规律,其中时间轴与图4流场云图的时间一致。
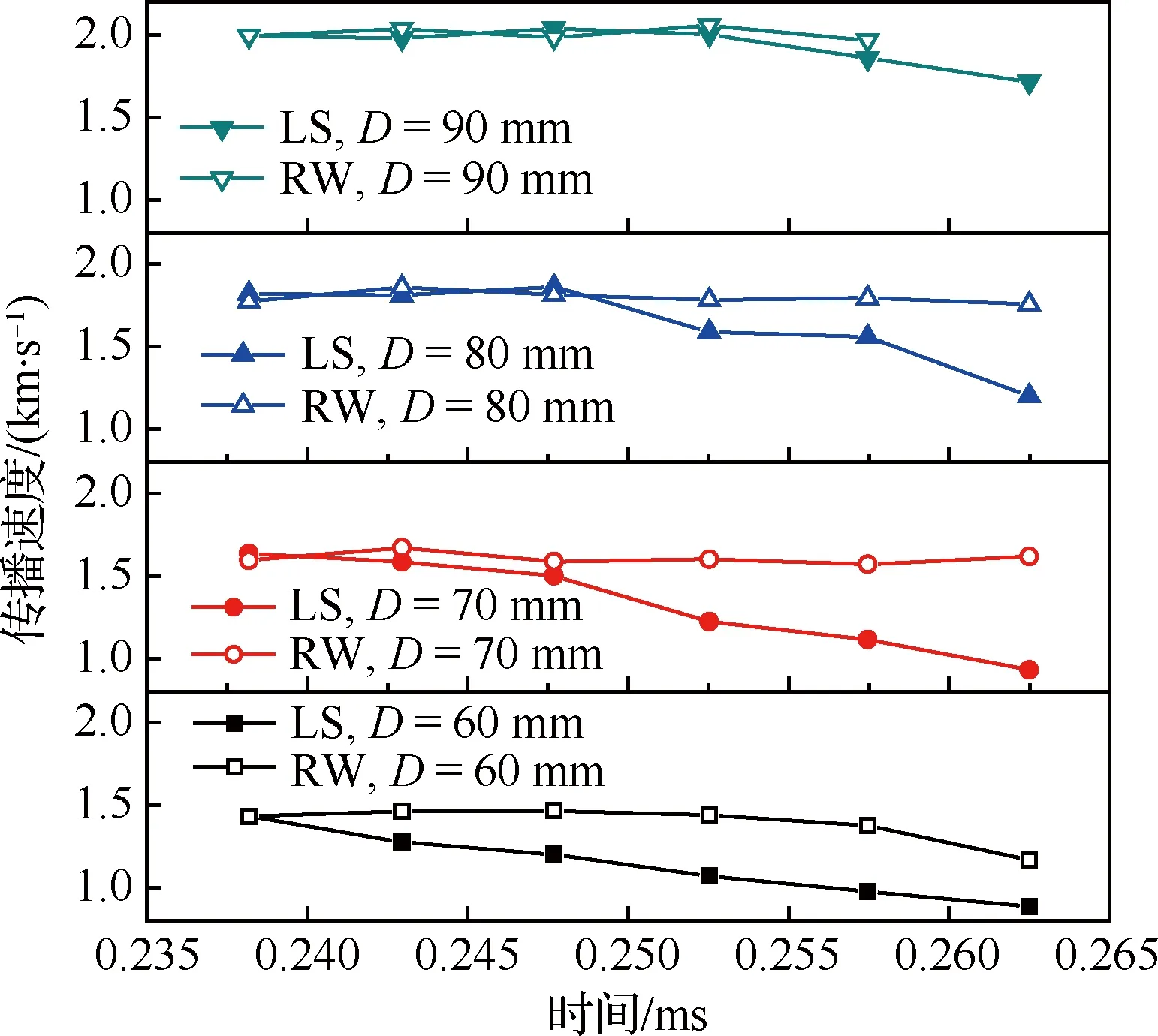
图9 不同径向位置前导激波与反射激波的传播速度Fig.9 Propagation velocities of leading shock wave and reflected wave in different radial positions
由图9可得,爆震波解耦前,随着直径D的增大,前导激波与反射激波的传播速度逐渐增大且保持一致,在直径90 mm附近,爆震波传播速度与理论值1 975.6 m/s接近,靠近内圆出口的速度受几何条件的限制,传播速度较低。未解耦流场的速度分布与稳定传播工况下流场内的速度分布相同,保证了爆震波与反射激波的相对位置不变,如图3及图4中未解耦时刻的流场云图所示。对于不稳定传播模态,随着时间的推移,靠近出口的前导激波速度首先开始下降,随之扩散到流场内部。随着直径的增加,前导激波速度依次开始下降,这与图4中压力云图的解耦顺序一致,爆震波从出口位置开始解耦,并逐渐往流场内部扩散。但由图9可得,反射激波的传播速度受解耦的影响较小,速度变化不大,且大于同一位置前导激波的传播速度。因此,后面的反射激波逐渐追赶前导激波,最终发生碰撞促使流场中局部热点的形成。
由图9发现,外圆附近的前导激波的传播速度几乎没有变化,两道激波的传播速度保持一致,这是因为外圆的收敛汇聚作用增强了爆震波强度,使之足以抵抗稀疏波的削弱而未发生解耦。
2.3 出口参数变化
由前所述,不稳定传播模态下,爆震波的“解耦—再起爆”过程对流场参数有很大的影响,该节重点研究爆震波的不稳定传播对出口速度、马赫数以及增压比的影响。
2.3.1 出口速度及马赫数
图10表示不同时刻下,计算域出口的径向分速度沿周向的分布。其中,t=0.238 2、0.257 5、0.271 5、0.292 3 ms分别为从爆震波的稳定段、解耦段、再起爆段和恢复稳定段选取的时刻,以此研究同一工况条件下旋转爆震波的不稳定传播对出口速度的影响。
由图10可得,在爆震波传播的不同阶段,出口径向速度沿周向的分布大致相同,径向速度的最大值在爆震波锋面附近取得,且不同时刻的速度峰值变化不大。说明爆震波的“解耦—再起爆”过程对径向速度分量影响很小。
除了径向速度的分布,本节还分析了出口平面的各速度分量及马赫数的平均值随时间的变化。图11为两个连续的“解耦—再起爆”周期内出口速度分量及马赫数平均值的变化曲线,其中,平均值为各参数在出口平面上沿周向的平均。
由图11可得,爆震波的不稳定传播对出口速度分量的平均值影响很小,在两个“解耦—再起爆”周期内,爆震波的解耦及再起爆过程会引起出口速度的轻微波动,但基本保持不变。出口平均马赫数的波动值较速度波动有所增加,但总体变化仍旧很小。由此说明,爆震波的不稳定传播对燃烧室出口的速度及马赫数影响不大。

图10 不同时刻下出口径向速度分量沿周向的分布Fig.10 Distribution of radial velocity component along circumference at exit for different moments

图11 出口马赫数和速度分量随时间的变化Fig.11 Variation of velocity components and Mach number at exit with time
2.3.2 出口增压比

(4)
式中:pout_total,t为t时刻燃烧室出口总压;ρout为燃烧室出口密度;ds为出口平面上网格的周向长度;l为燃烧室出口的周长。

(5)
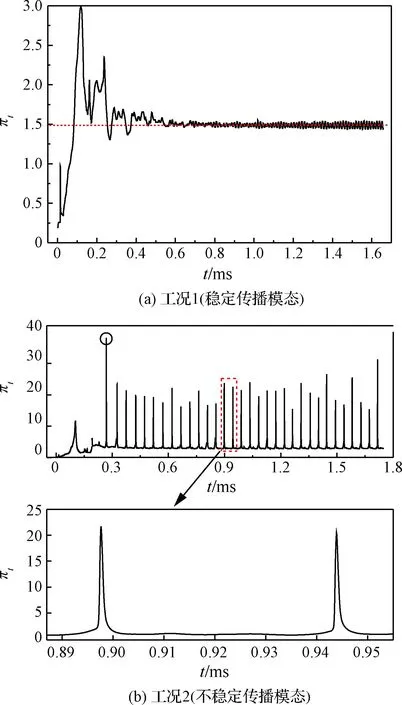
图12 出口增压比随时间的变化Fig.12 Variation of outlet pressure amplification ratio with time
图12(a)为稳定传播模态下(工况1)燃烧室出口增压比随时间的变化曲线,由图中曲线可得,随着时间的推移,出口增压比的波动逐渐减小,最后趋于稳定,稳定后增压比处于动态平衡状态,呈现周期性的振荡,但振幅很小。该工况条件下,燃烧室出口增压比的平均值大约在1.5左右。
图12(b)为不稳定传播模态(工况2)下燃烧室出口增压比随时间的变化曲线,由图可得,在开始时刻,出口增压比变化较为紊乱,随着时间的推移,增压比并没有趋于稳定,而是呈周期性波动,波动的幅值较高且不稳定。周期性波动的第1个峰值时刻(t=0.268 5 ms,图12(b)中实线圆圈所示)对应于爆震波第1个“解耦—再起爆”周期内重新起爆阶段的某一时刻,如图13所示,此时重新起始的爆震波强度较高,属于过驱爆震,且沿径向传播的横向爆震波(图6(d)中TDW)刚好传至出口位置,因此,爆震波附近的出口总压值迅速上升,增压比随之迅速跃升至峰值。随着时间的推移,沿径向传播的TDW从出口传出,且重新起始的过驱爆震波逐渐衰减为旋转爆震波,出口总压下降,增压比迅速衰减并维持一段较为稳定的值(如图12(b)局部放大图所示),直到下一个循环周期的爆震波再起爆阶段,增压比再次上升。

图13 工况2中压力云图的局部放大图 (t=0.268 5 ms)Fig.13 Detail view of pressure contours in Case 2 (t=0.268 5 ms)
由此可得,出口增压比跃升的主要原因是:再起爆时,流场中的局部热点遇到未燃气体区域形成强度较高的沿径向传播的横向爆震波TDW,TDW传播至出口位置时引起出口总压的急剧上升。由于计算域的内圆边界条件为无反射的出口边界,TDW传播至出口后直接传出并没有发生反射。因此,TDW从出口传出的下一时刻,爆震波附近总压迅速下降,增压比相应降低(见图12(b))。重新起始的周向过驱爆震波也在增压比的变化过程中起了一定作用。
由上述分析可得,出口增压比的循环周期应与爆震波“解耦—再起爆”的循环周期保持一致。经过计算,图12(b)所示燃烧室出口增压比的循环频率如图14所示。开始阶段,频率较低,随着时间的推移,频率逐渐增加,并在几个循环过后趋于动态稳定,频率均值约为21.6 kHz,频率值在均值附近上下波动,但波动幅值较小。另外,由解耦云图可得,爆震波“解耦—再起爆”的循环频率也有相似的变化,开始时频率较低,约为17.4 kHz左右,随着时间的推移,频率逐渐上升,最终频率值稳定在21.6 kHz附近并上下波动,这也验证了开始的推论:燃烧室出口增压比的循环周期与爆震波“解耦—再起爆”的循环周期保持一致,在该算例下,两者的循环频率皆为21.6 kHz。对图12(b)中动态稳定后的出口增压比取时间平均,得到不稳定传播工况2下出口增压比的平均值约为1.5,与稳定传播工况1的出口增压比数值相近。

图14 出口增压比的频率随时间的变化Fig.14 Variation of frequency of pressure amplification ratio at exit with time
3 结 论
通过对二维圆盘结构下旋转爆震波传播模态的数值计算,得到如下结论:
1) 得到了旋转爆震波不稳定传播模态的流场特点:不稳定传播模态下,旋转爆震波重复进行“解耦—再起爆”过程,爆震波的压力、温度以及传播速度皆随爆震波的解耦及再起爆发生变化。
2) 不稳定传播模态下,内圆扩张曲面的发散作用,使前导激波与火焰锋面分离,出口附近的爆震波首先解耦,解耦区域逐渐往流场内部扩张;外圆附近的爆震波因几何收敛作用增强而未发生解耦。爆震波解耦导致前导激波的传播速度降低,但反射激波受解耦的影响较小,传播速度大于前导激波,反射激波追赶上前导激波并发生碰撞,产生局部热点,重新起始爆震波。
3) 爆震波的不稳定传播对出口速度分量的平均值影响很小,爆震波的解耦及再起爆过程会引起出口速度的轻微波动,但基本保持不变。出口平均马赫数的波动值较速度波动有所增加,但总体变化仍旧很小。出口增压比受不稳定传播模态的影响较大,随时间呈周期性变化,变化幅值较高且不稳定。出口增压比的循环周期与爆震波“解耦—再起爆”的循环周期保持一致,稳定后两者的循环频率值皆为21.6 kHz。
[1] VOITSEKHOVSKII B V, MITROFANOV V V, TOPCHIYAN M E. Structure of the detonation front in gases[J]. Combustion, Explosion, and Shock Waves, 1969, 5(3): 385-395 (in Russian).
[2] BYKOVSKII F A, ZHDAN S A, VEDERNIKOV E F. Continuous spin detonations[J]. Journal of Propulsion and Power, 2006, 22 (6): 1204-1216.
[3] BYKOVSKII F A, ZHDAN S A, VEDERNIKOV E F. Continuous detonation of syngas-air mixtures in an annular flow-type cylindrical combustor[C]∥24th International Colloquium on the Dynamics of Explosions and Reactive Systems, 2013: 1-4.
[4] ANAND V, GEORGE A S, DRISCOLL R, et al. Characterization of instabilities in a rotating detonation combustor[J]. International Journal of Hydrogen Energy, 2015, 40(46): 16649-16659.
[5] ANAND V, GEORGE A S, DRISCOLL R, et al. Longitudinal pulsed detonation instability in a rotating detonation combustor[J]. Experimental Thermal and Fluid Science, 2016, 77: 212-225.
[6] RANKIN B A, RICHARDSON D R, CASWELL A W, et al. Chemiluminescence imaging of an optically accessible non-premixed rotating detonation engine[J]. Combustion and Flame, 2017, 176 (1): 12-22.
[7] ZHANG H L, LIU W D, LIU S J. Experimental investigations on H2/air rotating detonation wave in the hollow chamber with Laval nozzle[J]. International Journal of Hydrogen Energy, 2017, 42(5): 3363-3370.
[8] 刘世杰, 林志勇, 孙明波, 等. 旋转爆震波发动机二维数值模拟[J]. 推进技术, 2010, 31(5): 634-640.
LIU S J, LIN Z Y, SUN M B, et al. Two-dimensional numerical simulation of rotating detonation wave engine [J]. Journal of Propulsion Technology, 2010, 31(5): 634-640 (in Chinese).
[9] 刘世杰, 覃慧, 林志勇, 等. 连续旋转爆震波细致结构及自持机理[J]. 推进技术, 2011, 32(3): 431-436.
LIU S J, QIN H, LIN Z Y, et al. Detailed structure and propagating mechanism research on continuous rotating detonation wave[J]. Journal of Propulsion Technology, 2011, 32(3): 431-436 (in Chinese).
[10] MANABU H, FUJIWARA T, PIOTR W. Fundamentals of rotating detonations[J]. Shock Waves, 2009, 19(1): 1-10.
[11] EUDE Y, DAVIDENKO D M, GÖKALP I, et al. Use of the adaptive mesh refinement for 3D simulations of a CDWRE (Continuous Detonation Wave Rocket Engine): AIAA-2011-2236[R]. Reston, VA: AIAA, 2011.
[12] FROLOV S M, DUBROVSKII A V, IVANOV V S. Three-dimensional numerical simulation of the operation of a rotating-detonation chamber with separate supply of fuel and oxidizer[J]. Russian Journal of Physical Chemistry B, 2013, 7 (1): 35-43.
[13] TANG X M, WANG J P, SHAO Y T. Three-dimensional numerical investigations of the rotating detonation engine with a hollow combustor[J]. Combustion and Flame, 2015, 162(4): 997-1008.
[14] LI J, NING J G, ZHAO H, et al. Numerical investigation on the propagation mechanism of steady cellular detonations in curved channels[J]. Chinese Physics Letters, 2015, 32(4): 144-147.
[15] BYKOVSKII F A, ZHDAN S A, VEDERNIKOV E F, et al. Detonation of a coal-air mixture with addition of hydrogen in plane-radial vortex chambers[J]. Combustion, Explosion, and Shock Waves, 2011, 47(4): 473-482.
[16] NAKAGAMI S, MATSUOKA K, KASAHARA J, et al. Visualization of rotating detonation waves in a plane combustor with a cylindrical wall injector: AIAA-2015-0878[R]. Reston, VA: AIAA, 2015.
[17] ISHIYAMA C, MIYAZAKI K, NAKAGAMI S, et al. Experimental study of research of centrifugal-compressor-radial-turbine type rotating detonation engine: AIAA-2016-5103[R]. Reston, VA: AIAA, 2016.
[18] HIGASHI J, ISHIYAMA C, NAKAGAMI S, et al. Experimental study of disk-shaped rotating detonation turbine engine: AIAA-2017-1286[R]. Reston, VA: AIAA, 2017.
[19] 卓长飞, 武晓松, 封锋. 底部排气弹三维湍流燃烧的数值模拟[J].固体火箭技术, 2013, 36(6): 720-726.
ZHUO C F, WU X S, FENG F. Numerical simulation of three-dimensional turbulent combustion of the base bleed projectile[J]. Journal of Solid Rocket Technology, 2013, 36(6): 720-726 (in Chinese).
[20] 卓长飞, 武晓松, 封峰. 超声速流动中底部排气减阻的数值研究[J].兵工学报, 2014, 35(1): 18-26.
ZHUO C F, WU X S, FENG F. Numerical research on drag reduction of base bleed in supersonic flow[J]. Acta Armamentarii, 2014, 35(1): 18-26 (in Chinese).
[21] 马虎, 武晓松, 王栋, 等. 旋转爆震发动机数值研究[J]. 推进技术, 2012, 33(5): 820-825.
MA H, WU X S, WANG D, et al. Numerical investigation for rotating detonation engine[J]. Journal of Propulsion Technology, 2012, 33(5): 820-825 (in Chinese).
[22] 夏镇娟, 武晓松, 马虎, 等. 圆盘结构下旋转爆震波的二维数值研究[J]. 推进技术, 2017, 38(6): 1409-1418.
XIA Z J, WU X S, MA H, et al. Two-dimensional numerical simulation of rotating detonation wave in plane-radial structure[J]. Journal of Propulsion Technology, 2017, 38(6): 1409-1418 (in Chinese).
