基于Karhunen-Loève展开的分布式变体飞行器最优控制方法
2018-03-15龚春林赤丰华谷良贤方海
龚春林,赤丰华,谷良贤,方海
1.西北工业大学 航天学院 陕西省空天飞行器设计重点实验室,西安 710072 2.西北工业大学 航天飞行动力学技术重点实验室,西安 710072
传统飞行器大都采用固定的外形,设计方案是在多种飞行状态之间性能折中的结果,难以适应复杂的、具有大飞行包络的新一代飞行器需求[1]。变体飞行器可以根据飞行状态和环境变化,动态改变外形以获得最佳流场,保证大飞行包络下整体性能最优,对提高飞行器性能具有很大的应用潜力,得到国际飞行器领域广泛关注。
变体飞行技术发展至今,可大致划分为集中式和分布式两类。早期集中式变体技术采用简单机构实现变后掠、变展长等单个或少数变形自由度,以适应多种飞行任务。虽然集中式变体技术已经在B-1B枪骑兵、F-14雄猫、V-22鱼鹰等已服役飞行器中得到应用,并具有结构简单、可靠、易实现等优点,但变形方式有限,不能对流场进行精细控制,难以适应高动态复杂飞行任务。
近年来,随着智能材料和结构、微小型驱动器以及分布式控制理论[2]的发展,实现多自由度连续变形的分布式变体技术逐渐得到关注。其采用多个驱动器实现局部或全局的连续变形,可以在很大范围内快速精细地调整微观流场,以适应飞行状态连续动态变化,是未来变形飞行技术的主要发展方向,成为当前研究者们关注的焦点。美国宾夕法尼亚州立大学设计了一种分布式变形结构,通过八面体腱驱动柔顺细胞桁架实现变形[3],如图1(a)所示。Grumman公司设计了图1(b)所示的自适应桁架翼肋结构,通过分布式驱动器改变机翼横截面翼型[4]。南京航空航天大学研制了图1(c)所示的分布式驱动变形机翼实验平台对分布式控制的问题展开研究[5,7-8]。洛克希德·马丁公司设计了通过响应电脉冲的记忆膜改变机翼形状的MPUAV。美国DARPA资助NextGen研发了一种滑动蒙皮的变形翼设计方案[9]。杨智春和解江[10]设计了一种应用于变体机翼的柔性后缘自适应机翼。李伟等[11]对变体翼梢小翼的伸缩栅格进行了研究,发现其可对飞机起飞阶段的流场进行改善。

图1 分布式变体结构Fig.1 Distributed morphing structure
变体技术使得飞行器具有更强的灵活性和任务适应性,但也带来了新的挑战问题,即面临动态变化的飞行任务,如何以最优的方式控制飞行器的变形过程。
Falcão等[12]对NACA0015的可变形翼尖小翼的两个可变翼型参数进行了优化,获得了满足多种高度和速度飞行状态下的最优解。Holland等[13]采用多学科优化框架,对无人机机翼展长、弦长、后掠角等变形参数在多个典型飞行条件下的飞行性能进行了优化。Dale等[14]利用多学科优化技术针对机翼弯度的变形开展了研究。以上研究的优化问题仅针对少数的典型飞行状态,如高低空巡航、低速巡逻等,所获得的一般是“分档”变形规律,不适用于飞行状态连续变化的飞行任务。
Vale等[15]利用最优控制理论对两自由度变形翼(变弯度和变展长)的变体飞机进行了优化。Mir等[16]对变后掠翼无人机变体滑翔轨迹展开最优控制,得到了最优的变体规律。Ryan和Lewis[17]对可变翼炮弹轨迹中的变体规律进行了优化,研究了翼面形状随轨迹的规律。严旭飞和陈仁良[18]用最优控制方法研究倾转旋翼机的最优动态倾转过渡过程,并得到了最优操纵策略。李焕焕[19]针对Z型可折叠翼变形飞行器和可伸缩变后掠翼变形飞行器的不同飞行任务进行了轨迹优化。以上研究虽然考虑了变体飞行器在整个飞行轨迹的最优控制问题,但主要针对包含少数变形自由度的集中式变形技术,不适用于理论上具有无穷变形自由度的分布式变体技术。
在变体飞行器控制方面,很多学者也开展了大量的研究。Nigam等[20]发展了包含子系统辨识和最优控制两个部分的仿生变体飞行器自适应控制系统。Guo等[21]对仿海鸥翼的变体飞行器,分别采用变体翼和传统舵进行轨迹和姿态的动态控制。高仁璟等[22]对基于压电纤维复合薄膜驱动器的变体进行了研究,提出了一种满足类翼面平板结构的弯曲、扭转和弯扭型面精确变形控制需求的布局与控制参数协同优化设计方法。董朝阳等[23]对一类存在执行机构故障的分布式结构变体飞行器的控制分配问题,提出一种基于布谷鸟搜索算法的容错控制方法。但是,目前变体控制研究大都只针对飞行过程中从某一状态过渡到另一状态,由于变体导致的动力学模型变化带来的过渡过程控制问题。
与现有研究相比,本文重点解决在飞行任务连续、动态变化情况下,如何实现分布式变形过程优化问题。该问题本质上是一个变量在时间和空间上均具有无穷维度的优化问题,求解困难在于:① 现有最优控制方法无法直接求解无穷维控制量问题;② 由于变形引起的气动模型数据和动力学模型维度增加,计算量呈级数增长,优化求解困难。现有研究对该问题涉及较少。
本文第1节给出了变体飞行器动力学通用模型,并给出原始问题的数学模型。第2节针对原问题求解困难,首先采用Karhunen-Loève展开方法对变形域进行空间离散,将其转化为有限维度控制参数和几何模态描述,将原问题转化为有限维度最优控制问题;然后,利用Kriging方法构造了与变形控制参数相关的气动性能参数代理模型,解决直接采用气动数值计算方法的计算困难;最后,应用hp伪谱法构造了该最优控制问题的求解过程。第3节针对某翼型可分布式变形的飞行器算例,实现全弹道上翼型随时间变形规律的优化。
1 分布式变体最优控制问题
分布式变体飞行器的特点是可以实现多自由度连续变形,最优控制的目的是找到最适合当前飞行任务的变形规律,使得其相对某种指标具有最优性。在给出该最优控制问题的求解方法之前,首先考虑变形导致的气动力作用于飞行器引起飞行轨迹的变化,给出变体飞行器一般动力学模型,在此基础上提出最优控制问题。
1.1 变体飞行器动力学模型
变体飞行器的飞行概念如图2所示。不考虑地球旋转和地球曲率,具有分布式变体特征的飞行器在纵向对称平面内的动力学模型可统一表示为
(1)

图2 变体飞行示意图Fig.2 Morphing procedure during flight

L=qSCL(Ma,y,α,Ω)
D=qSCD(Ma,y,α,Ω)
(2)
式中:q为飞行动压;S为参考面积;CL、CD分别为升、阻力系数,与飞行状态(马赫数Ma、迎角α、高度y)以及变形域Ω相关。
1.2 最优控制问题
飞行器变体的目的是通过改变外形以最优的方式适应飞行环境和完成既定的任务,是一个典型的优化问题。对式(1)所示的动力学模型,该优化问题可描述为
1) 目标函数
根据变体飞行器执行任务的不同,目标函数的选择不同。但其一般表达式为

(3)
式中:γ(·)和K(·)为与终点条件和过程相关的目标函数;f(t)为运动轨迹;tf为任务结束时刻;u为控制变量。如以燃料消耗最少作为设计指标,则目标可简化表示为
(4)
2) 控制变量

Ω∈[Ωmin,Ωmax]}
(5)
式中:下标max和min分别表示控制变量的上下边界。对变形函数Ω,其上下边界由变形执行机构的可达行程和变形结构材料的可变形程度决定。
3) 状态变量
状态变量s反映了任意时刻飞行器的状态,由控制变量决定,可表示为
s={θ∈[θmin,θmax],x∈[xmin,xmax],
y∈[ymin,ymax],m∈[mmin,mmax],
V∈[Vmin,Vmax]}
(6)
4) 约束模型
变体飞行器在飞行过程中受到动压q、法向过载ny、起点和终点状态变量等约束限制。约束变量c表示为
ny=|Lcosα+Dsinα|/(mg)≤nymax,
(7)
式中:ρ为大气密度;下标0和f分别表示起点和终点条件;上标*表示状态变量的约束值。
至此,建立起考虑变形函数Ω(t)的分布式变体飞行器的动力学模型和最优控制问题,可表述为:在状态变量s遵循动力学方程式(1),以及满足约束c的前提下,获得最佳的控制变量随时间变化规律u*(t),使得目标函数J最小化。
2 分布式变体最优控制方法
1.2节提出的是一个典型的最优控制问题。由于变形域Ω(t)是曲线或曲面随时间变化的函数,因此控制变量在空间上具有无穷维度。现有的最优控制问题求解方法包括直接法或间接法,主要针对有限维度控制变量如何进行求解,不能解决无穷维度控制变量的优化问题。本文研究思路是通过构造一种空间上的离散方法,将函数Ω转换为有限维度变形控制变量描述,从而将原问题转化为有限维控制变量的最优控制问题。以下将基于Karhunen-Loève(K-L)展开方法[24]进行离散。
相对一般飞行器的最优控制问题,变形控制变量的存在增加了气动分析的维度,将会使得气动计算量呈级数增长,给优化问题求解带来严重的计算负担。本文提出采用Kriging方法构建代理模型解决该问题。
以上两个问题解决后,可以按照一般最优控制问题处理。本文采用hp自适应伪谱方法进行求解。
2.1 基于K-L展开的变形控制变量离散
对于一个曲面或者曲线,可直接将其离散成有限个控制结点,通过改变控制结点位置来对曲面或曲线进行变形。控制结点数即为可变形的维度。对随时间变化的曲面,有
Ω(x,y,z;t)=0
(8)
将其离散成s个随时间变化的坐标结点:
ni(t)∈Ω(x,y,z;t)=0 (9)
每一个结点都是一个独立的变形维度,其变形过程可以表示为
ni(t)=ni(0)+Δni(t)
(10)
式中:ni(0)为结点i的初始坐标;Δni(t)为结点i在t时刻相对初始坐标的变形量。

首先将变形量Δni(t)描述为一随机场量ψ(n,t),(n,t)表示空间坐标和时间变化,通过将其展开为协方差方程的特征函数(正交函数)的无穷维线性组合[25],并采用一组基本模态和对应特征值描述该场量,则控制变量数可减少为模态数。
每个节点随时间的变化可以表示为
Δni(t)=ψi(n,t)·ni
(11)
式中:ni为结点i的单位法向量;ψi(n,t)为变形的随机场量在i点的分量。
随机场量ψ(n,t)可表示为
(12)
式中:λ1≥λ2≥…≥λi≥…≥0和zi分别为协方差函数的特征值和特征向量。任意两离散结点i、j的协方差函数可表示为
(13)
Xi(t)作为非相关随机变量,均值为0,方差为1。ψ0(n)是随机场的均值,对于表示变形量的随机场来说,ψ0(n)=0。
在L∞(Γ)×L2(O)中,若特征值衰减得很快,则可取式(12)中前d项ψd精确表示ψ:
(14)

(15)
至此,将原无穷维度的变形函数Ω(t)变化规律转化为由d维变量控制的变化规律。
以RAE2822翼型外形参数为例,对上述方法进行验证。将翼型外形离散成192个离散点,选择前163个离散点进行变形。协方差函数选择为


图3 翼型离散后计算的特征值Fig.3 Eigenvalues of discrete airfoil

图4 前9个特征值对应的翼型模态Fig.4 Airfoil modalities of the top 9 eigenvalues
2.2 变体飞行器气动代理模型建立方法
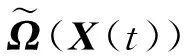
D=qSCD(Ma,y,α,X)
L=qSCL(Ma,y,α,X)
(16)
相对一般飞行器的气动力模型,由于引入了d个变形控制变量,将会给最优控制问题求解带来极其严重的计算负担。若在每个变形控制变量取M个点,则插值点的数量增长为非变体飞行器的Md倍。为了解决该问题,本文利用拉丁超立方抽样(Latin Hypercube Sampling,LHS)[26]和Kriging法[27]结合的方法,建立与变形控制变量相关的气动代理模型,可以大幅缩减气动计算维度。所采用步骤如图5所示。
首先采用LHS方法,在变量X(t)=[X1(t)X2(t) …Xd(t)]组成的试验空间取N个样本点X1,X2,…,XN,步骤如下:
步骤1将每个变量i的区间[Xi,min,Xi,max]分为N个子区间,在取样时以相同概率选择每个子区间。

步骤3重复步骤2,直到抽取N个变形控制变量样本点{X1,X2,…,XN}。

以CD为例,可采用Kriging方法得到任意未采样点的预测值:
(17)
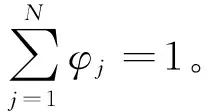

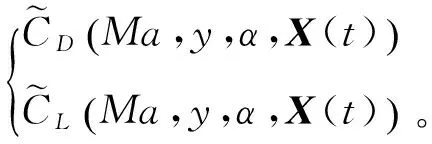

图5 气动代理模型建立步骤Fig.5 Steps of aerodynamic surrogate model
2.3 基于hp伪谱方法的最优控制问题求解
通过2.1节的离散,将原最优控制问题转化为一个有限维度的最优控制问题,可以采用直接法或间接法进行求解。对变体飞行器气动非线性较强的轨迹优化问题,为了加快求解时的收敛速度,对动力学方程进行无量纲处理。结合2.2节构造的气动代理模型,最终得到的动力学模型为
(18)
式中:“—”表示该变量的无量纲形式。
考虑到该问题控制变量维度较高,设计空间复杂,选择直接法中计算性能较高的hp自适应伪谱方法[29-30]。首先在一系列Gauss点上将控制变量u和状态变量s离散,并以这些离散点为结点构造Lagrange插值多项式来近似控制变量和状态变量,可将最优控制问题转化为具有一系列代数约束的参数优化问题,即非线性规划问题进行求解。对优化算法,选择计算效率较高的序列二次规划方法。
2.4 求解流程
综上,本文研究的分布式变体飞行器最优控制问题求解流程如图6所示。主要步骤包括:



图6 分布式变体飞行器最优控制问题求解流程Fig.6 Flow chart of solution for optimal control distributed morphing flight vehicle
步骤3采用hp自适应伪谱法,对变形域的参数化模型在时间维度进行离散,对整个飞行轨迹进行一种考虑分布式变体的优化求解,以达到最优的性能(如最小燃料消耗量)。
3 变翼型飞行器算例
假设某变翼型飞行器的翼型采用可分布式变形的RAE2822翼型,翼的平面形状为平直翼,外形如图7所示。该算例的任务目标是通过同时控制发动机燃油消耗、迎角以及翼型的变形过程,使得其以最节省的燃油量从给定地点到达指定地点。如图8所示,飞行器可以有多条飞行轨迹完成这样的飞行任务,而如何选择一条最优的轨迹来达到目标参数最优,是一个典型的最优控制问题。

图7 平直翼变翼型飞行器Fig.7 Morphing airfoil of straight wing aircraft
图8 变翼型飞行器飞行轨迹规划Fig.8 Flight path design for morphing airfoil aircraft
算例的主要参数如表1~表3所示。该算例主要用于验证第2节发展的方法,利用建立的变体飞行器动力学模型,以燃料消耗量作为评价指标,研究在大海拔跨度条件下,利用基于K-L展开的变翼型方法和基于hp自适应伪谱法的最优控制方法对变翼型飞行器性能的提高,并与采用固定翼型飞行器的优化结果进行比较。为了突出主要因素,忽略由于机翼变形引起的机体的升、阻力变化,且假设没有横向气流流动。在优化问题中,飞行器的气动特性变化主要与翼型的变形相关。

表1 控制变量Table 1 Control parameters

表2 状态变量Table 2 State parameters

表3 约束模型Table 3 Constraint model
3.1 RAE2822翼型变形描述
为了探究K-L展开应用于翼型变形的效果,如2.1节所述方法,只取前2个特征值和特征向量来表示随机场ψ,可得
(19)
选取X1(t)、X2(t)作为变形控制变量,以式(19)得到的ψ(n,t)作为变形量,沿着翼型离散点的法线方向变形,即
(xi,yi)new=(xi,yi)old+ψi·ni
(20)
图9显示了初始RAE2822翼型和当X1=-0.002、X2=0.006时的变形情况。注意翼型的尾部不发生变形,以此来保证气动计算时的收敛。

图9 初始RAE2822和变形后的RAE2822翼型Fig.9 Original and transformed RAE2822 airfoils
3.2 气动代理模型构造结果
优化过程中,2个变形控制变量的区间取为[-0.006,0.006]。利用LHS方法,抽取N=20个点,抽样结果如图10所示。

图10 变形参数LHS结果Fig.10 LHS results of morphing parameters
对初始RAE2822翼型和样本点上的变形RAE2822翼型,利用CFD计算工具FLUENT计算气动力系数CD和CL数据库。计算所用黏流模型为sutherland,湍流模型为SSTk-Ω模型,离散方法为Least Squares Cell Based,二阶迎风格式。图11为RAE2822的2D结构气动网格。
利用Kriging方法,选用高斯模型作为变异函数模型,选用二阶多项式作为回归模型,建立气动代理模型,可得到各个飞行状态下不同变形控制变量(X1(t),X2(t))的气动代理模型。图12给出Ma=0.4、飞行高度H=0 km、α=4°时CL的代理模型结果,白色小球表示样本点。可见,代理模型结果与样本点吻合得很好。

图11 RAE2822翼型的2D结构气动网格Fig.11 2D structured aerodynamic grid of RAE2822 airfoil

图12 升力系数代理模型Fig.12 Surrogate model of lift coefficient
3.3 优化结果及分析
利用hp自适应伪谱方法对变翼型飞行器和固定翼型飞行器的轨迹进行优化。图13和图14分别给出固定翼型飞行器和变翼型飞行器的控制变量和状态变量曲线图。可以看出,利用hp伪谱法得到的弹道优化结果与基于最优控制变量积分的弹道一致,证明了hp方法应用于变体飞行器最优控制的可行性。另外,从优化结果可以看出,变翼型飞行器和固定翼型飞行器优化结果均达到了设计要求,完成飞行任务目标的时间分别为75.7 s和72.5 s。
从图15和图16可以看出,在整个飞行过程中,变翼型飞行器的速度比固定翼型飞行器的速度慢,迎角也较小,且没有达到8°的上界,变翼型飞行器在较小速度和较小迎角的条件下,依然可以完成飞行任务。可见,变翼型飞行器的升力有所提高,采用较小的迎角即可完成给定任务,从而减小了飞行器的阻力。图17显示变翼型飞行器和固定翼型飞行器最终的质量分别为43 000 kg和42 801 kg。变翼型飞行器燃料消耗比固定翼型飞行器节省了2.76%。
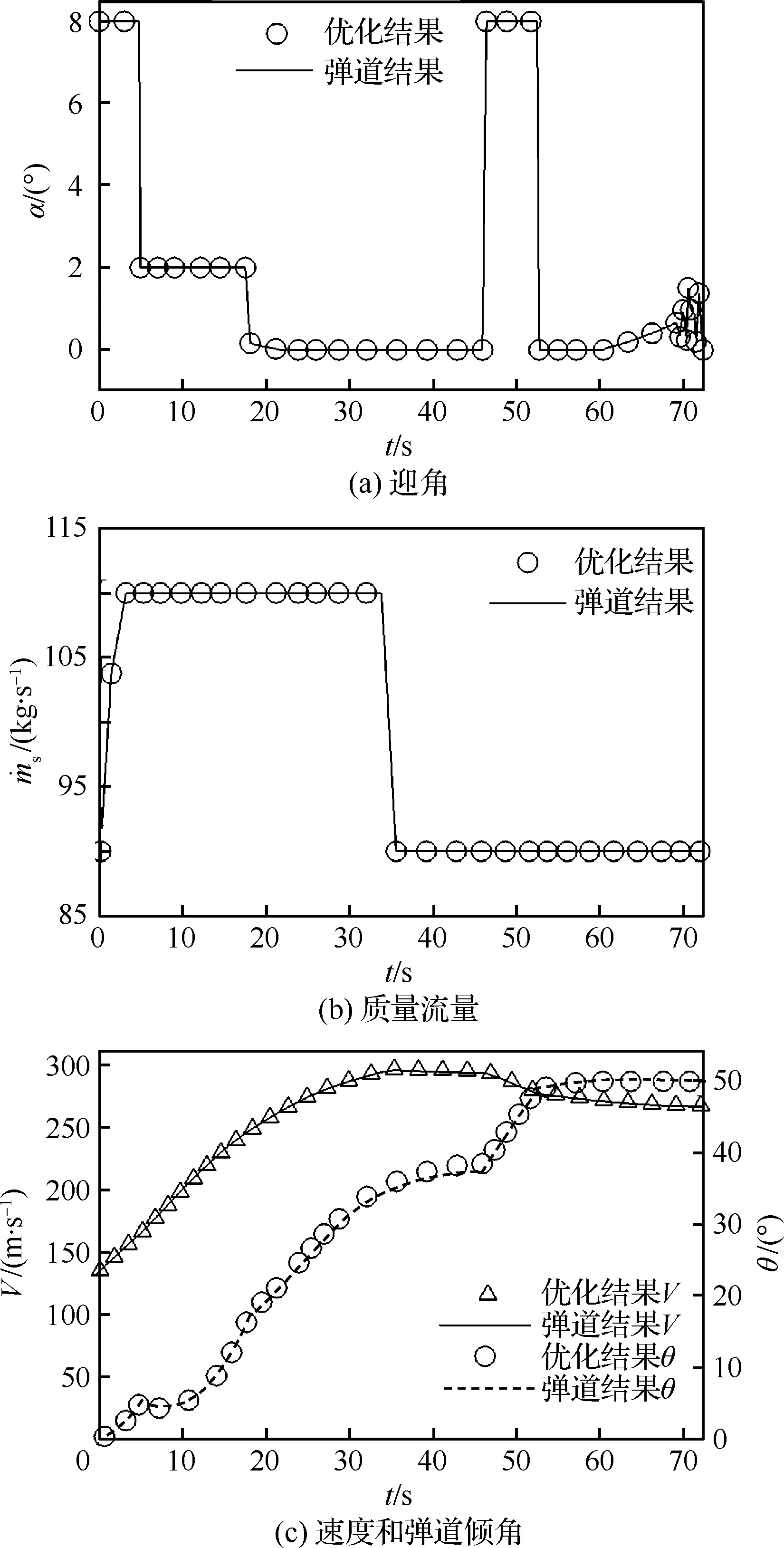
图13 固定翼型飞行器控制变量和状态变量优化结果Fig.13 Optimization results of control and state variables of fixed airfoil aircraft

图14 变翼型飞行器控制变量和状态变量优化结果Fig.14 Optimization results of control and state variables of morphing airfoil aircraft

图15 变翼型与固定翼型飞行器速度对比Fig.15 Comparison of velocities of morphing airfoil aircraft and fixed airfoil aircraft

图16 变翼型与固定翼型飞行器迎角对比Fig.16 Comparison of angles of attack of morphing airfoil aircraft and fixed airfoil aircraft
从图18可以看出,在飞行初始阶段,由于和固定翼型飞行器相比,变翼型飞行器发动机质量流量较小,导致推力较小,且变翼型飞行器速度和迎角较小,故其弹道高度在飞行初始阶段较固定翼型飞行器弹道高度低,如图19所示。而由于变翼型飞行器改善了不同飞行条件下的升阻力,变翼型飞行器在飞行任务后半段上升速度较快,仅比固定翼型飞行器的飞行时间超出3.2 s即完成了飞行任务。
图20给出在不同飞行阶段最优翼型与固定翼型的对比,c为弦长,h为厚度。虽然在本算例中,由于变形控制变量的变化范围较小,翼型的可变形范围也较小,但依然减小了飞行器的燃料消耗量。
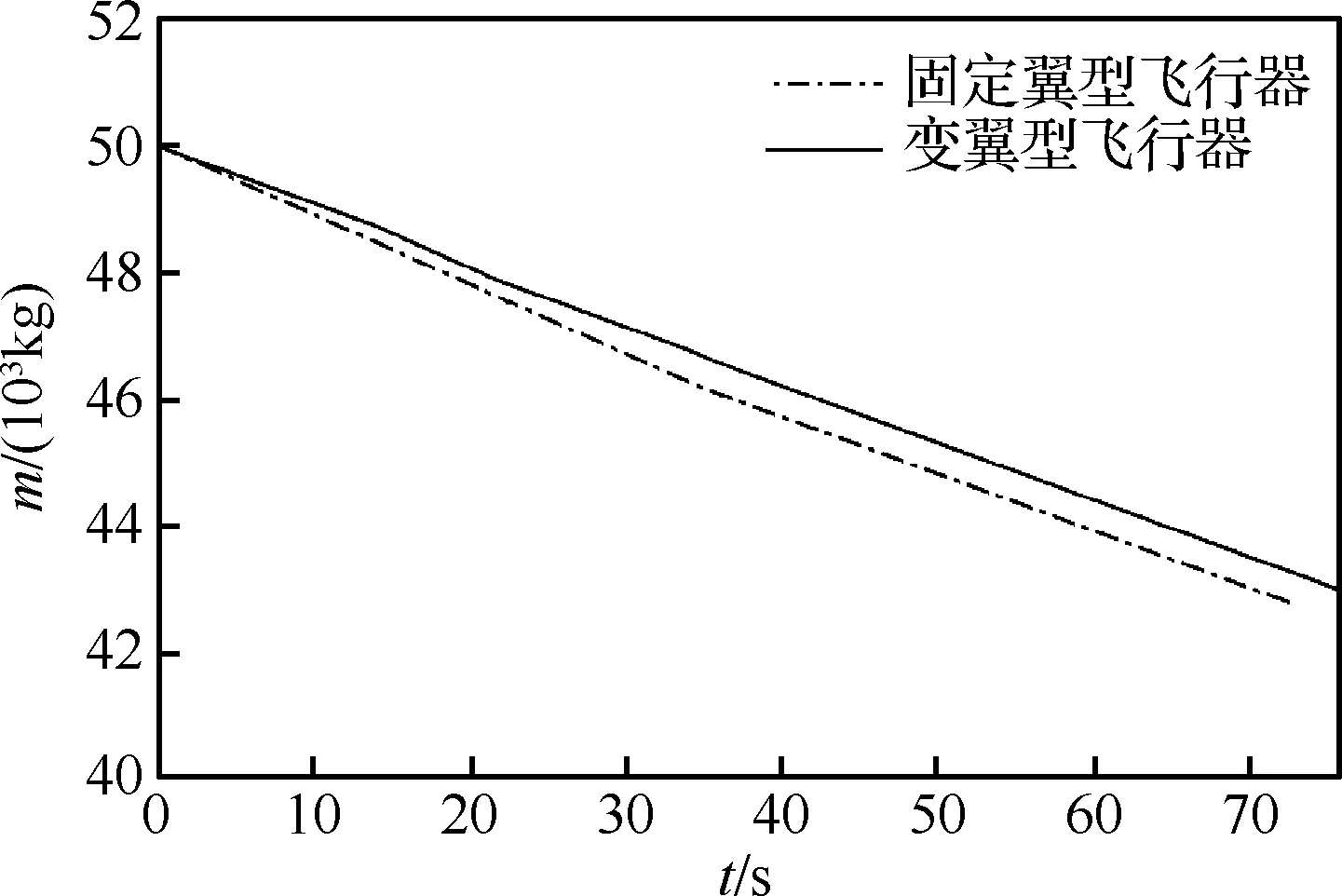
图17 变翼型与固定翼型飞行器质量对比Fig.17 Comparison of masses of morphing airfoil aircraft and fixed airfoil aircraft
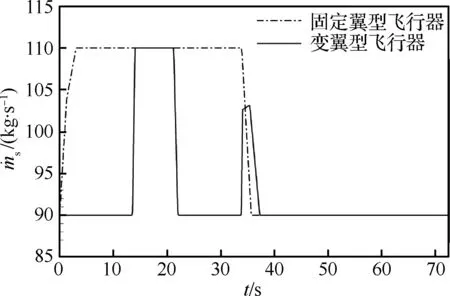
图18 变翼型与固定翼型飞行器质量流量对比Fig.18 Comparison of mass flow rates of morphing airfoil aircraft and fixed airfoil aircraft

图19 变翼型与固定翼型飞行器纵向对称平面弹道对比Fig.19 Comparison of trajectories of morphing airfoil aircraft and fixed airfoil aircraft of longitudinal symmetry plane


图20 变翼型飞行器翼型随时间变化Fig.20 History of airfoils of morphing airfoil aircraft during whole trajectory
4 结 论
随着智能材料和驱动技术的发展,分布式变体飞行技术的实现和应用已经逐渐成为可能。但其带来更高飞行性能的同时,也给飞行器带来了如何进行多维度控制的新问题。本文针对分布式变形规律设计问题,在建立的变体飞行器动力学模型的基础上,提出了一种最优控制方法。利用Karhunen-Loève展开对分布式变体飞行器变形域进行展开,将空间无限维的变形域转换为少数变形控制变量的变化规律;结合拉丁超立方抽样(LHS)和Kriging方法建立了分布式变体飞行器的气动代理模型,解决了控制变量维度增加带来的气动计算问题;在时间维度上,利用hp自适应伪谱方法对参数化的变形域进行离散,并对飞行轨迹进行最优控制。最后以分布式变翼型飞行器为例,利用所建立的求解方法对其飞行轨迹进行优化,达到了最小燃料消耗量的优化目的,验证了本文方法的有效性。
1) 采用基于Karhunen-Loève展开的变形控制变量离散,可以通过较少的变形控制变量对所有离散结点进行变形,使其变形范围不仅仅局限于几种构型,每一个参数化结点坐标都可以变化,具有了更大的自由度。随着变形域离散结点增多,可以向更大范围的变形设计空间发展。
2) 所建立的变体飞行器气动代理模型,仅需较少的样本点就能够拟合整个设计空间的气动参数,显著降低了计算成本。
3) 对变翼型飞行器与固定翼型飞行器的最优控制问题进行了分析,对比结果显示采用通过分布式变翼型最优控制,能以较小的速度和迎角完成同样的飞行任务,减少了2.76%的燃料消耗量。
本文建立的方法对分布式变体飞行器具有共性,能扩展到机体/弹体等更为复杂的变体形式,为未来变体飞行技术发展提供参考和支持。由于目前所采用的算例主要是为了验证方法的可行性,因此选择的变形控制变量较少,且变形控制变量约束范围较小,优化对飞行性能的提升较为有限。在实际工程应用中,为了更精确地表示分布式变形的特点,应选取更多特征值来表示整个变形域的参数化模型,以提高变形自由度,使其在满足计算成本约束的前提下,最大程度地发挥变体飞行的优势。另外,现有变形方法对大变形量的处理还存在一定问题,限制了变体对飞行性能的提高,需要进一步改进变形方法。
[1] 杜厦, 昂海松. 改变飞机变体机翼优化方法与气动特性仿真[J]. 计算机仿真, 2013, 30(3): 88-91.
DU X, ANG H S. Optimization method and aerodynamic character simulation of morphing wing[J]. Computer Simulation, 2013, 30(3):88-91(in Chinese).
[2] KEULEN B V.H∞-control for distributed parameter systems: A state-space approach [M]. Boston,MA:Birkhäuser Boston, 1993:101-129.
[3] RAMRAKHYANI D S, LESIEUTRE G A, FRECKER M I, et al. Aircraft structural morphing using tendon-actuated compliant cellular trusses[C]∥Morphing Aircraft Structures Using Tendon Actuated Compliant Cellular truss, 2005:1615-1621.
[4] AUSTIN A F, NOSTRAND W C V. Shape control of an adaptive wing for transonic drag reduction [J]. Smart Materials and Structures, 1995, 2447:45-50.
[5] 文哲远. 分布式驱动变体飞行器控制的仿真系统研究[D]. 南京:南京航空航天大学, 2012:11-21.
WEN Z Y. Research on simulation system of distributed driven morphing aircraft control [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012:11-21(in Chinese).
[6] 何真. 变体飞行器基础控制问题研究[D]. 南京:南京航空航天大学, 2009:77-95.
HE Z. Research on basic control problem of morphing aircraft [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009:77-95 (in Chinese).
[7] 吴俊. 变形翼分布式协同控制技术研究[D]. 南京:南京航空航天大学, 2011:82-93.
WU J. Research on distributed coordinated control technology of morphing wing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011:82-93 (in Chinese).
[8] 陆宇平, 何真. 变体飞行器控制系统综述[J]. 航空学报, 2009, 30(10):1906-1911.
LU Y P, HE Z. A survey of morphing aircraft control systems[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10):1906-1911(in Chinese).
[9] RODRIGUEZ A. Morphing aircraft technology survey[C]∥AIAA Aerospace Sciences Meeting and Exhibit. Reston, VA: AIAA, 2013:1-6.
[10] 杨智春, 解江. 柔性后缘自适应机翼的概念设计[J]. 航空学报, 2009, 30(6):1028-1034.
YANG Z C, XIE J. Concept design of adaptive wing with flexible trailing edge[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6):1028-1034(in Chinese).
[11] 李伟, 熊克, 陈宏,等. 用于变体翼梢小翼的伸缩栅格研究[J]. 航空学报, 2011, 32(10):1796-1805.
LI W, XIONG K, CHEN H, et al. Research of retractable grid applied to morphing winglet[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10):1796-1805(in Chinese).
[13] HOLLAND M, MOORE B, FERGUSON S. 'Transforming' for stability and aerodynamic performance in a reconfigurable UAV[C]∥12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston, VA: AIAA, 2012.
[14] DALE A, COOPER J E, MOSQUERA A. Adaptive camber-morphing wing using 0-υ honeycomb[C]∥AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston, VA: AIAA, 2013.
[15] VALE J, LAU F, SULEMAN A. Optimal control and energy balance evaluation of a morphing aircraft[C]∥AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston, VA: AIAA, 2013.
[16] MIR I, MAQSOOD A, AKHTAR S. Optimization of dynamic soaring maneuvers for a morphing capable UAV[C]∥AIAA SciTech Forum. Reston, VA: AIAA, 2017.
[17] RYAN K, LEWIS M. Trajectory optimization studies of long range morphing projectiles[C]∥AIAA Atmospheric Flight Mechanics Conference. Reston, VA: AIAA, 2012.
[18] 严旭飞, 陈仁良. 倾转旋翼机动态倾转过渡过程的操纵策略优化[J]. 航空学报, 2017, 38(7): 720865.
YAN X F, CHEN R L. Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 720865(in Chinese).
[19] 李焕焕. 新概念变形飞行器飞行轨迹优化设计[D]. 哈尔滨: 哈尔滨工业大学, 2015:38-53.
LI H H. Optimal flight trajectory design of new concept morphing aircraft[D]. Harbin:Harbin Institute of Technology,2015:38-53 (in Chinese).
[20] NIGAM N, ZHANG Y, CHEN P, et al. Adaptive control and actuation system development for biomimetic morphing[C]∥AIAA/AHS Adaptive Structures Conference. Reston, VA: AIAA, 2015.
[21] GUO T, HOU Z, ZHU B. Dynamic modelling and active morphing trajectory-attitude separation control approach for gull-wing aircraft[J]. IEEE Access, 2017, 5:17006-17019.
[22] 高仁璟, 张莹, 赵剑,等. 面向结构形状控制的压电纤维复合薄膜驱动器布局方式与控制参数协同优化设计[J]. 机械工程学报, 2016, 52(18):177-183.
GAO R J, ZHANG Y, ZHAO J, et al. Integrated design optimization of MFC-layout form and control parameters for morphing structural shapes[J]. Journal of Mechanical Engineering, 2016, 52(18):177-183(in Chinese).
[23] 董朝阳, 路遥, 江未来,等. 基于布谷鸟搜索算法的一类变体飞行器容错控制[J]. 航空学报, 2015, 36(6):2047-2054.
DONG Z Y, LU Y, JIANG W L, et al. Fault tolerant control based on cuckoo search algorithm for a class of morphing aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6):2047-2054(in Chinese).
[24] FUKUNAGA K, KOONTZ W L G. Application of the Karhunen-Loève expansion to feature selection and ordering[J]. IEEE Transactions on Computers, 1970, C-19(4):311-318.
[25] SCHILLINGS C, SCHULZ V. On the influence of robustness measures on shape optimization with stochastic uncertainties[J]. Optimization and Engineering, 2015, 16(2):1-40.
[26] 方开泰. 均匀试验设计的理论、方法和应用——历史回顾[J]. 数理统计与管理, 2004, 23(3):69-80.
FANG K T. Theory, method and application of uniform experimental design—History review[J]. Journal of Applied Statistics and Management, 2004, 23(3):69-80(in Chinese).
[27] KRIGE D G. A statistical approach to some basic mine valuation problems on the witwatersrand[J]. Operational Research Quarterly, 1953, 4(1):18.
[28] 李新,程国栋,卢玲.空间内插方法比较[J]. 地球科学进展, 2000, 15(3):260-265.
LI X, CHENG G D, LU L. The comparison of spatial interpolation methods[J]. Advances in Earth Science, 2000, 15(3):260-265(in Chinese).
[29] GANDHI M. Trajectory optimization algorithm studies[J]. Mathematics, 2015, 15(2):267-281.
[30] 张博渊, 宗群, 鲁瀚辰,等. 基于hp自适应伪谱法的四旋翼无人机编队轨迹优化[J]. 科技导报, 2017, 35(7):69-76.
ZHANG B Y, ZONG Q, LU H C , et al. Trajectory optimization of quad-rotor uav formation using hp-adaptive pseudospectral method [J]. Scientia Technologica Sinica, 2017, 35(7):69-76(in Chinese).
