浅析高三数学数形结合的解题技巧与方法

史亚鹏

【摘要】众所周知，数学作为高中的重点学科，是一名学生在高考中是否取得好的成绩、与其他人拉开差距的关键所在.因此，在高三复习阶段，教师应该重视对学生数学思想的培养.数形结合体现了很强的数学思想.本文将针对北师大版高三数学，来浅谈在数学教学过程中，运用数形结合时，应该有着怎样的技巧和方法.

【关键词】高三数学；数形结合；技巧和方法

在高中的数学学习过程中，数形结合的运用是比较频繁的，这是一种极具数学思想的方法，在高中的数学知识结构框架中，占据着很大的比重.数形结合是根据问题出现的内在原因，运用数字和图形或是图表的方式来解析问题.由于数形结合的方法较为实用，因此，在高中的数学解题时，经常运用数形结合的方法，因此，懂得数形结合的解题技巧也就极为重要.

一、简述数形结合

所谓数学，就是数字的学问，而为了更好地研究数，人们往往将形融入数中，做到数形结合，已达到更为形象化.在高中的数学教育过程中，数形结合的方法是很常见的，在解题过程中，学生根据问题所给的条件以及已有的结论，运用图表或是图形等方式来对其代数意义进行研究，从而解决问题，这种方式让数字的运算显得更加形象化.与此同时，数形结合的运算方式能够将一些复杂的问题进行简单化，让学生能够很容易地明白问题中的含义与联系.

二、运用技巧

任何的方法都有其运用技巧，数形结合的方法也有其运用技巧，因为其具有实用性，因此，如何能够巧妙地将数形结合的方法进行运用是每一位高中数学教师应当思考的问题，下面提出三点技巧，以供参考.

（一）将数字形态转变为图形形態

数学之所以难倒了大多数的高中学生，主要原因就在于其数字知识的抽象化，生涩难懂，过多的代数公式令人头疼.如果将这些数字以图形的形式表现出来，就会显得更加直观、形象，比较容易理解.将数字形态转变为图形形态，使得学生的思维得以变得活跃，从而解题思路更加清晰，解题也变得更加容易，学生的个人能力也逐渐地加强了.

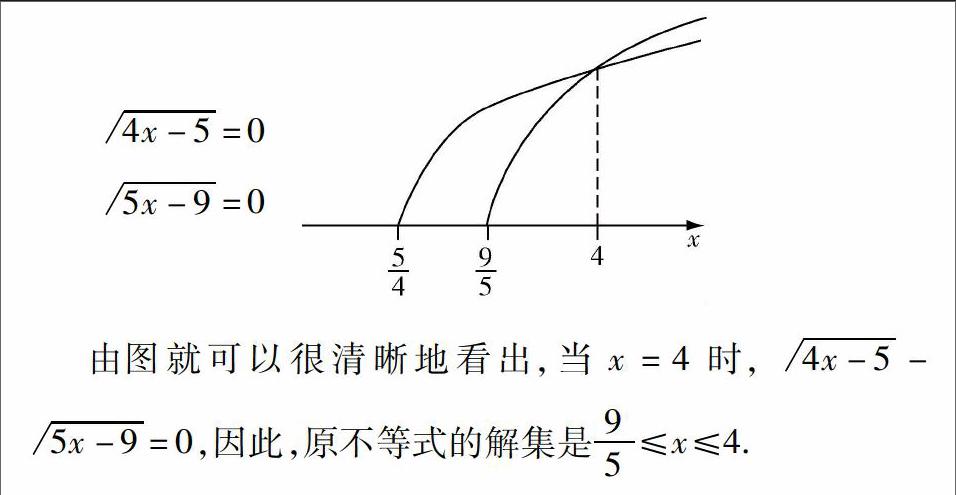
例如，北师大版高中数学教材中，其中有一题是运用了数形结合的方式来解题.题目为4x-5-5x-9≥0，虽然学生觉得这种题目不难，也在脑海里寻找着各种公式来求解这道题，但有时候往往会忽略掉一些关键的点，例如，学生们往往会忽略掉根号下的数字必须大于零的这个前提.如果能够让学生在解题的时候，按照题目所给的式子来描画出二维图像，就能够根据图像得到这个不等式的解.而如果按照一般的解题思路，则会先去求解根号内的数字在大于0的时候所组成的不等式组，而且很多学生很容易就将之忽略掉.接着将两边的式子进行平方，将之前的式子转化成整式，最后再来寻求不等式的交集.但是如果运用数形结合的方法来解题的话，我们可以从下图来看：

4x-5=0

5x-9=0

由图就可以很清晰地看出，当x=4时，4x-5-5x-9=0，因此，原不等式的解集是95≤x≤4.

从这个例子中，我们可以很清楚地认识到，在解决不等式或不等式组时，可以将数字转化为图形，这样可使题目更加直观，更加容易让学生理解，并能够轻松地将题目的答案解出来.这种方法拓宽了学生的解题方法，新颖的解题方式也解放了学生的解题思路，利用更为直观的图形来解题也大大地培养了学生的思维能力和善于发现问题的核心的能力.

（二）将图形转化为数字理论

虽然利用图形来解题显得更为直观方便，但是任何事物都不是完美的，图形在简便的同时，却少了数字概念应有的准确性和逻辑性.而数学是一门需要很强逻辑性的学科，因此，如果单单运用图形来解题的话，容易出现一些失误，而且也不容易让人信服.于是这时就很有必要利用数形结合，将图形转变成数字，用巧妙的方法来解决问题.

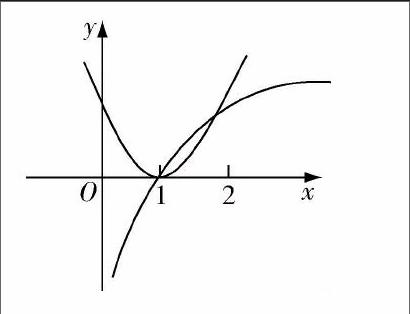
例如，北师大版高中数学中的一个例题：（x-1）2≤logbx在x∈（1，2）内恒成立，求实数b的取值范围.在这道题中，假设f1（x）=（x-1）2，f2（x）=logbx，想要x∈（1，2）时，使得不等式成立，则只需要求得f1（x）=（x-1）2在x∈（1，2）

上的图形位于f2（x）=logbx的图形下方就可以了.当01时，如图所示，想要使得f2（x）在x∈（1，2）上的图像处于f1（x）图像的上面，则只需要做到f1（2）≤f2（2），即（2-1）2≤logb2，因此，1

从这道例题可以看出，在求取具体的数值时，这个数学问题是难以在只适用图形的情况下，来准确将数值求取出来的.因此，应当将图形转化为数字，这样有助于学生在理解题目的情况下，快速地进行解题.

（三）多媒体助力数形结合

在高考的复习过程中，教师在课堂上的每一分每一秒都是十分重要的，因此，教师要将那些十分复杂的、具有抽象化的知识和题目以最快的速度来进行讲解是十分麻烦的.因此，为了提高效率，教师可以运用多媒体来实现数形结合的解题，这样教师既节省了在课堂上花费大把时间来进行画图讲解，也使得教师少吸食粉笔灰，保持了健康.且多媒体展示出来的图形可以通过软件来不断地变化，也显得更加形象，更容易让学生理解.

综上所述，高中数学教师，特别是高三的数学教师，在学生进行复习的时候，应当巧妙运用各种方法来解题，而数形结合是较为常见的，也是比较实用的方法之一，教师应当用好技巧，使得数形结合的方法能够更加便于学生进行解题.在教授方法时，教师应当提醒学生在解题时，要全面地看待，要数形结合，不要有数忘形或是有形却忘了数，应记住条件中出现的各种解题可能，从而将题目的答案完整地呈现出来.

【参考文献】

[1]江士彦.浅析高中数学数形结合的解题技巧[J].读与写，2015（10）：89.

[2]范粤.高中数学教学中渗透数形结合思想应注意的几个问题[J].数理化学习，2014（7）：52-53.

[3]杜路敏.浅析高中数学教学中数形结合思想的运用和实施[J].学周刊，2013（22）：141.