弹性箔片轴承-盘式永磁电机转子系统轴向冲击响应*
2018-03-14程文杰李维钟斌樊红卫肖玲刘刚李明
程文杰 李维 钟斌 樊红卫 肖玲 刘刚 李明
(1.西安科技大学 理学院,西安 710054) (2.西安科技大学 机械工程博士后科研流动站,西安 710054)(3.西安科技大学 机械学院,西安 710054)
引言
AFPM电机通常用于低速、大扭矩领域,如船用、车用发动机[1-3].鉴于AFPM电机转子轴向尺寸短,具有自冷却效果,当其应用于高速时,会具有更高的转矩密度、更佳的散热能力和更紧凑的结构.采用新型非晶合金材料代替常规硅钢,能有效降低电机铁耗[4,5],随着非晶合金等新型超薄软磁材料的发展,高速AFPM电机已经逐渐引起了人们的关注[6].文献[6]设计了一台高速AFPM电机,工作转速18 000rpm,功率4kW,整机效率90%,用于废气能量回收.文献[7,8]开发了一台设计转速1 000 000rpm的两相供电超高速AFPM电机,并进行了32 000rpm的试验验证.AFPM电机是一种本质意义上的三维电磁结构[9].考虑到盘的振动和定转子间磁吸力的影响,AFPM电机的轴向气隙厚度一般较大,当转子偏心时会形成非均匀的气隙,气隙磁密与气隙厚度的关系呈非线性[10,11].文献[12]研究了轴向磁化永磁斥力轴承的刚度,建立了永磁刚度矩阵.求解GFBs-转子系统在时域中的响应较困难且非常耗时,因为它不仅涉及到三类方程(转子动力学方程、气膜雷诺方程,箔片结构方程)的耦合,而且GFBs的动态气膜压力与轴颈的扰动频率相关.为了加快仿真时间,Hassini和Arghir[13-15]提出用二阶有理函数来估算轴承的非线性气膜力.另一种处理方法则是放弃刚度和阻尼的概念,将箔片结构方程带入气膜雷诺方程进行迭代计算,直接求解轴承的气膜力.此法虽然完全计入了轴承气膜力的非线性项,但是在预测GFBs-转子系统动力学行为时,又需要将上面两个方程与转子动力学方程进行反复迭代[16],增加了计算量.鉴于此,Bonello和Pham[17-19]放弃了这种迭代思路,提出了一种“同时求解”策略,即采用某种数学变换将原方程组写成状态方程形式,然后利用矢量技术求解时域或频域内的响应.事实上,为进一步地减轻计算负担,人们引入了一些假设(对转子、气膜、箔片之间相互作用的动力学本质进行折衷),提出了刻画轴承气膜力的经验模型.文献[20,21]研究了径向磁通电机转子系统的耦合振动.
目前关于GFBs支承的AFPM电机转子系统振动的研究较少,对于该类型的电机,转子在输出周向电磁转矩的同时,还作为一种“磁轴承”,与GFBs并联工作,这种“附加轴承”效应会对转子轴向、横向振动产生影响.迄今为止,关于AFPM电机转子“附加轴承”效应的研究还鲜见报道.因此,本文将采用轴承刚度来描述该“附加轴承”效应,建立GFBs-AFPM电机转子系统动力学模型,分析转子受轴向冲击时,轴向GFBs以及AFPM电机的“附加轴承”刚度对系统瞬态响应的影响规律.
1 箔片轴承支承的高速AFPM电机
AFPM电机将永磁体放置于转子盘上,使得转子轴向长度大大缩短,径向尺寸略增大,如图1所示.另外,高速旋转的转子盘相当于一个离心风扇,可实现电机的自冷却.以上特点使得AFPM电机具有更高的转矩密度、更佳的散热能力和更紧凑的结构.对于那些对空间有严格要求的驱动系统,如燃料电池汽车发动机、飞机发动机、飞机空气循环系统等,AFPM电机将是更好的选择.
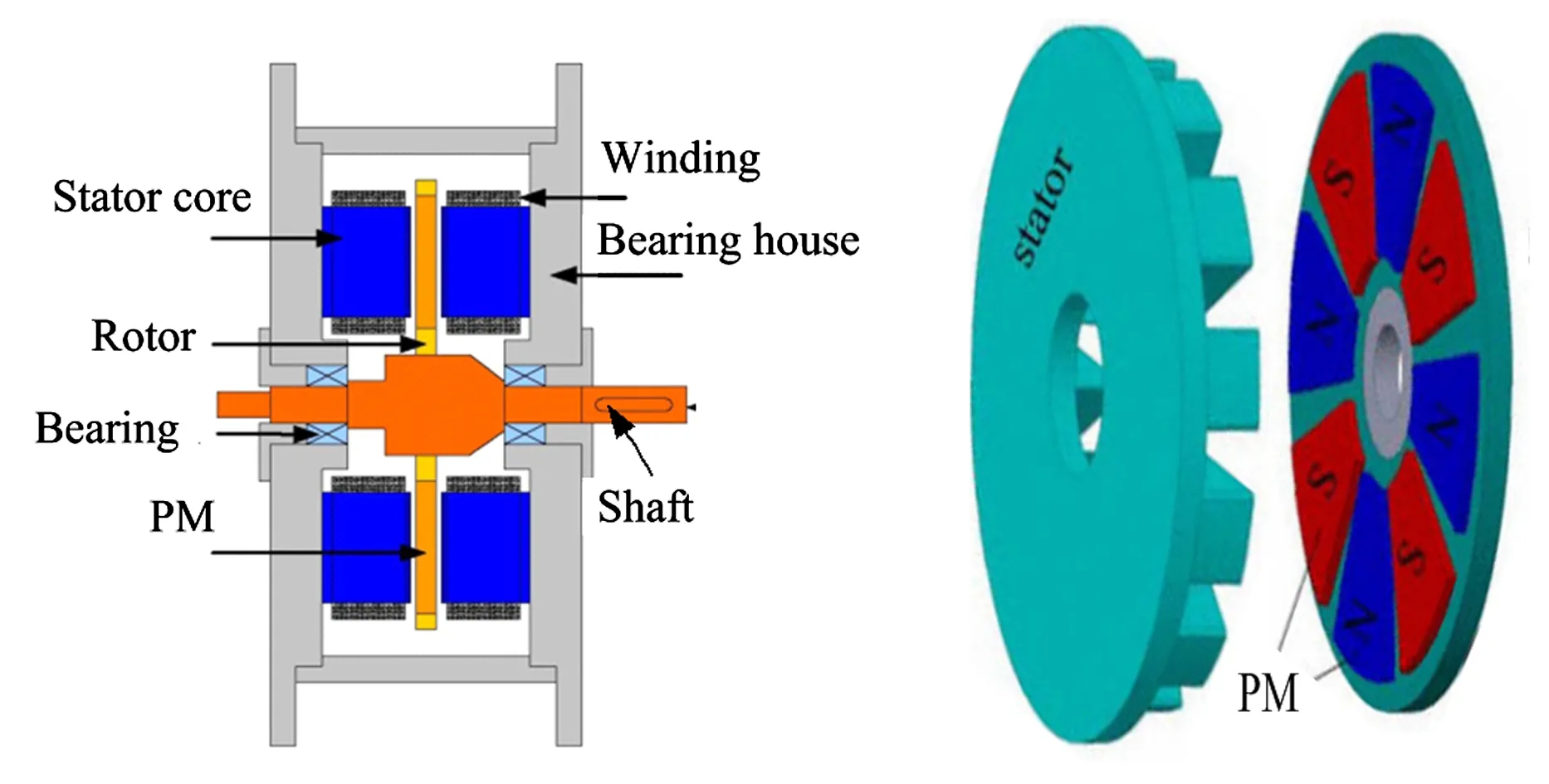
图1 GFBs支承的单定子单转子AFPM电机结构Fig.1 Single stator-single rotor AFPM motor supported by GFBs
2 刚性转子动力学方程
为简化计算,特做如下假设:
(a)推力轴承、径向轴承和永磁轴承对转子动力学的影响用刚度和阻尼系数描述,不计入推力轴承在水平、竖直方向上的交叉刚度和交叉阻尼;
(b)推力盘在轴向振动和偏转时,也会感应出电涡流,产生涡流阻尼,由于该涡流阻尼较小,可以忽略;
(c)不考虑气膜温度对轴承、永磁体性能产生的影响;
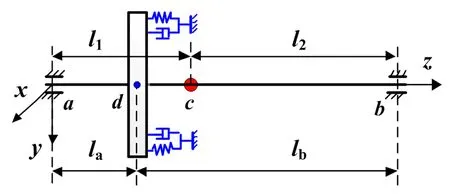
图2 不对称刚性转子系统Fig.2 Asymmetric rigid rotor system
气体动压轴承支承下的刚性转子可等效成图2所示的形式,转子长度为l,转子质心c点距两端支承点距离分别为l1和l2,推力盘中心d点距两端支承点距离分别为la和lb,转子左端(a端)和右端(b端)两轴承支承处的动态位移依次为x1、y1、x2、y2.如果不考虑推力盘上的磁吸力和轴承推力,仅仅考虑径向GFBs对转子振动的影响,则转子运动微分方程的矩阵形式如下:
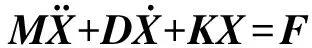
(1)
其中,
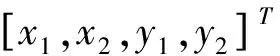
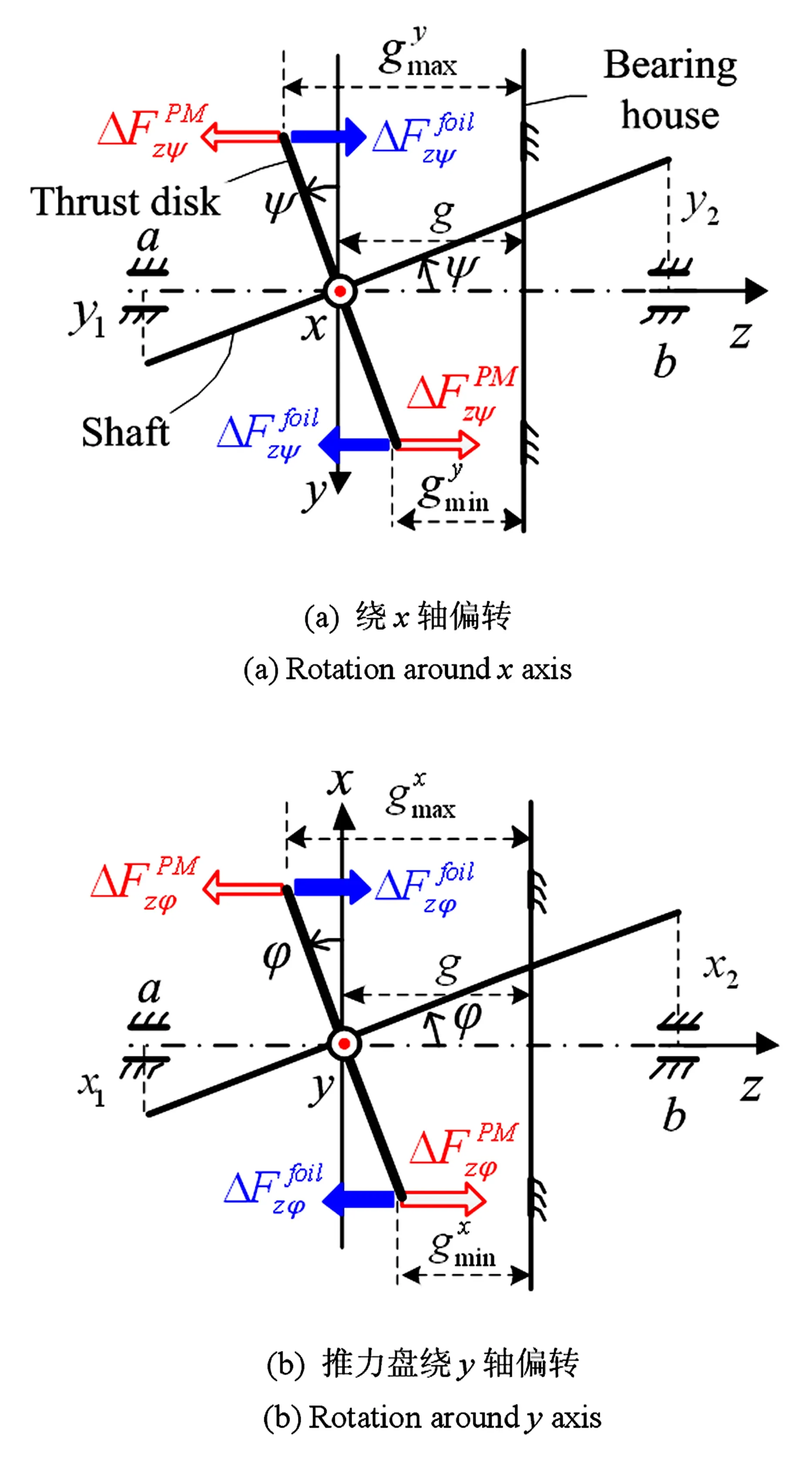
图3 推力盘偏转时引起的附加轴承力Fig.3 Additional bearing force caused by the deflection of the thrust disk
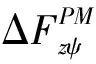
(2)
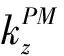
(3)
由于径向轴承的振动量y1和y2相对于转子长度l非常小,所以有:
(4)
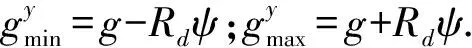
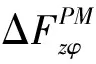
(5)
(6)
另外,有:
(7)
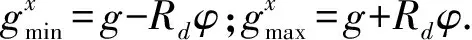
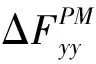
(8)
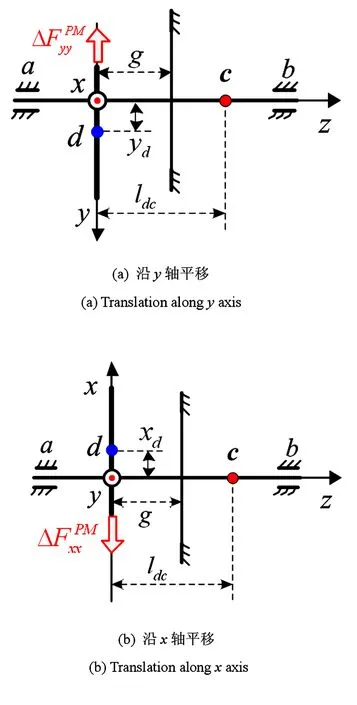
图4 推力盘平行涡动时引起的附加轴承力Fig.4 Additional bearing force caused by the parallel vortex of the thrust disk
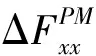
(9)
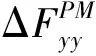
(10)
其中,h1=lb/l,h2=la/l.
当计入推力盘偏转效应和平行涡动效应后,则式(1)所示的转子横向振动微分方程如式(11)所示,其中各矩阵的元素将会发生变化,具体如附录A所示.
(11)
转子轴向振动微分方程如式(12)所示:
(12)
其中,
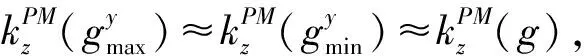
(13)
3 算例
根据小位移假设,与即盘的轴向振动、偏转和轴颈的横向振动对径向轴承和轴向轴承稳态工作点的影响可以忽略,在计算中,径向轴承、推力轴承的气膜刚度和阻尼以及永磁轴承的刚度可以近似为不变.如果计入箔片的非线性结构刚度效应,则箔片轴承的等效刚度和等效阻尼分别为:
(14)
(15)
上式中的keff0和deff0分别是轴颈无涡动时,箔片轴承的等效刚度、阻尼,角标air代表气膜参数,角标foil代表箔片结构参数.实际中的轴颈一般出现同步涡动,量纲分析表明当轴颈的涡动频率ω→∞时,keff0和deff0趋近于同步涡动时的等效刚度和阻尼.
轴承-转子系统动力学方程中各参数如表1所示,其中气膜的刚度和阻尼系数选取的是对应的箔片轴承为刚性表面情形下的参数.箔片的结构刚度用二次函数描述,为kfoil_xx=kfoil_yy=kfoil_zz=k0+k1y+k2y2,径向箔片的结构阻尼记为dfoil_xx=dfoil_yy,轴向箔片的结构阻尼记为dfoil_zz.
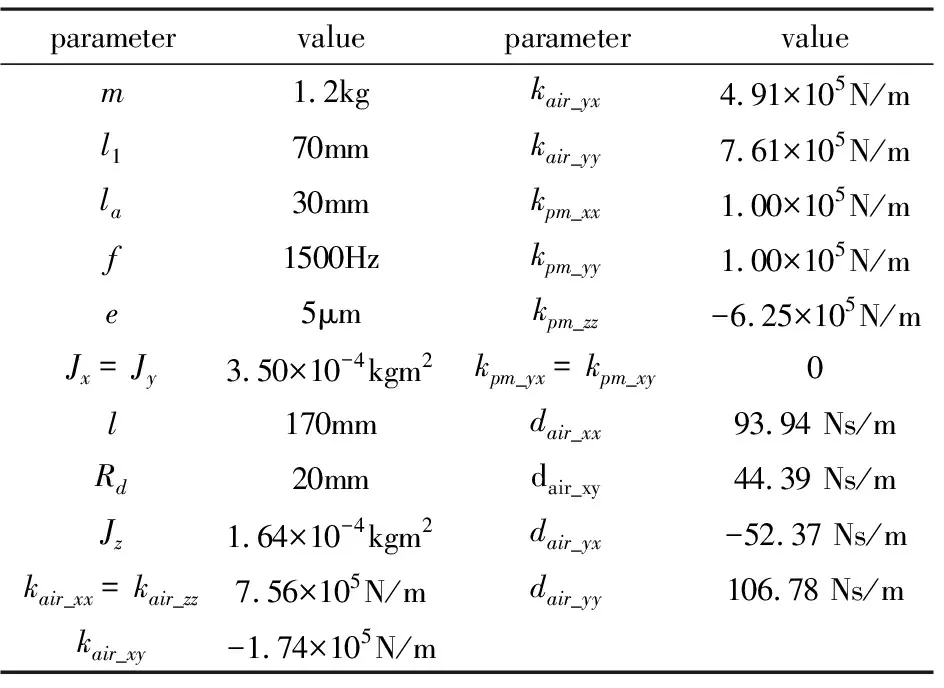
表1 表1 轴承-转子系统参数Table 1 Parameters of the bearing-rotor system
4 结果分析
当k0=5×106,k1=-5×109,k2=2×1014,表明箔片具有变化的结构刚度,dfoil_xx=dfoil_yy=350Ns/m,dfoil_zz=100Ns/m.转子只在1.7s受到一个30N,作用时间0.03s的轴向冲击力.
将式(11)和式(13)联立,写成状态方程的形式,给定初始条件后,通过龙格库塔法进行迭代求解,结果如图5所示.图5(a)为转子轴向位移z的响应曲线,z在0.2s后就达到稳定值零,这是因为轴向方向无恒定的激励源,在1.7时受轴向冲击的影响,出现波动,峰值达到450μm,0.15s后又趋于零.
为了考察轴向冲击是否对横向振动产生影响,做出了转子a端的位移x1随时间的响应曲线,如图5(b)所示.x1在1.5s时才趋于稳定值(幅值5μm),在1.7s后x1随时间并没有明显的变化,说明轴向冲击对横向振动的影响非常小.图5(c)显示了转子最终处于稳态时的轴心轨迹,可见两支承处的横向振动幅值均小于10μm.
当k0=6×106,k1=0,k2=0(表明箔片具有恒定的结构刚度),其它条件不变,仍然施加一样的轴向冲击力,计算结果如图6所示.图6(a)所示,受到冲击作用影响,转子轴向位移z在1.7s后振幅突然增大,峰值约为1000μm,在0.12s后又趋于零.相对于变结构刚度箔片,恒定结构刚度箔片在常数项上大,但是随着位移的增大,变结构刚度箔片的刚度会远大于恒定结构刚度箔片的刚度(即前者会变得非常硬),因为箔片越硬,等效刚度越大,因此转子振幅会减小(450μm<1000μm).
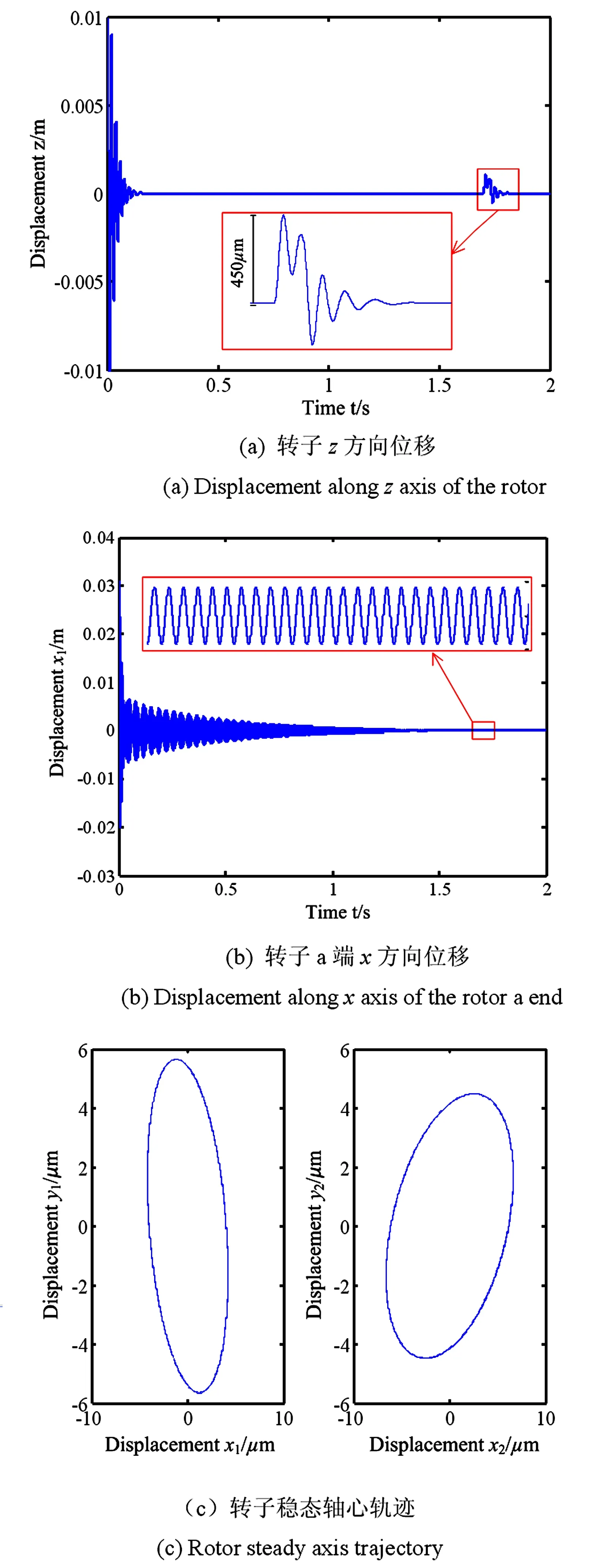
图5 具有变结构刚度箔片转子系统的瞬态响应Fig.5 Transient response of the rotor system with variable structure stiffness foil
相对于图5(b),图6(b)显示转子a端的位移x1收敛非常快,在0.15s后即达到稳态.与图5(b)类似,图6(b)中也没有轴向冲击对位移x1有明显影响的痕迹.这说明,不管是轴向箔片刚度是可变还是不可变,轴向冲击只对转子轴向振动有影响,对横向振动几乎无影响.最终的轴心轨迹如图6(c)所示.
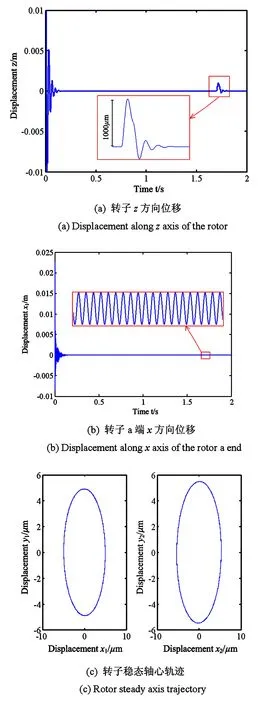
图6 具有恒定结构刚度箔片转子系统的瞬态响应Fig.6 Transient response of the rotor system with constant structure stiffness foil
对比以上两种箔片的计算结果发现,轴向冲击对横向振动的影响均非常小.刚度箔片,随着位移增大,箔片越硬,等效刚度越大,因此转子振幅会这是因为轴向冲击力作用在转子的轴线上,主要引起推力盘的轴向位移,而不会造成推力盘的大幅偏转,进而也就不会显著地对横向振动产生影响.对于变结构减小,但是等效阻尼会减小,所以转子振荡时间会加长.因此在设计时,要注意箔片结构刚度和结构阻尼的合理匹配,以保证转子在轴向冲击下的轴向震荡时间和振幅均不超过允许值.
当k0=5×106,k1=-5×109,k2=2×1014,kpm_zz=-7.3×105N/m,即将永磁轴承的负刚度绝对值增大,计算结果如图8所示,可见转子轴向位移z在1.7s后振幅突然增大,峰值接近1000μm,在0.15s后又趋于零.这个振幅已经远远超出了轴向箔片轴承的正常工作间隙,而且对永磁轴承的刚度的影响是不能忽略的.计算表明,永磁体的负刚度绝对值超过7.3×105N/m时,轴向振幅会发散,但实际的推力盘两端都有轴向箔片轴承约束,这说明永磁体的负刚度绝对值过大时,推力盘会撞到箔片轴承.在设计箔片轴承-盘式永磁电机转子系统时,需要综合考虑永磁轴承刚度和箔片轴承刚度,阻尼之间的匹配.
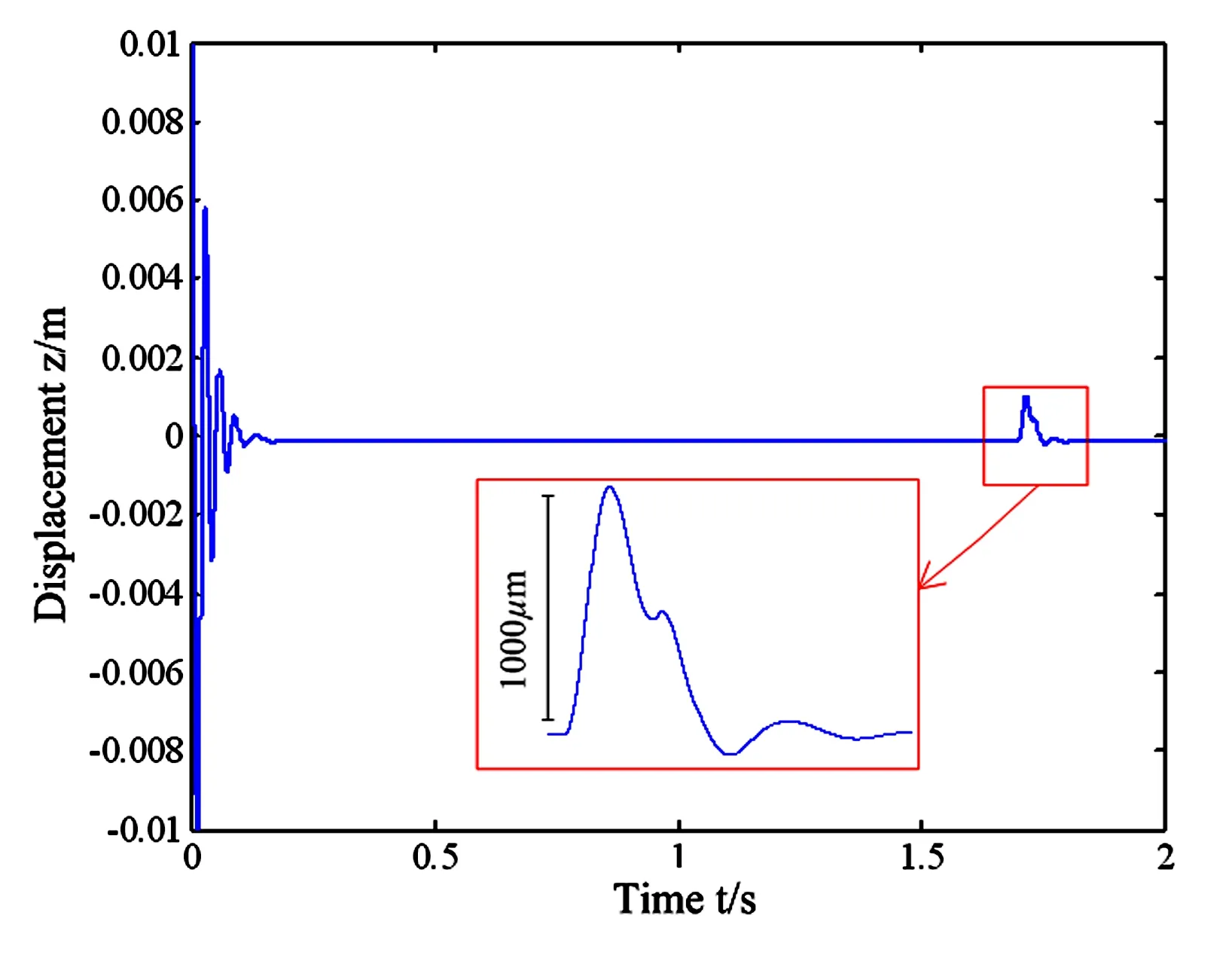
图7 永磁轴承负刚度增大时转子z方向位移Fig.7 Displacement along z axis of the rotor with a large PM bearing stiffness
5 结论
1)当转子受到一个作用时间0.03s,30N的轴向冲击力时,计算发现轴向冲击对横向振动的影响非常小.这是因为轴向冲击力作用在转子的轴线上,主要引起推力盘的轴向位移,而不会造成推力盘的大幅偏转,进而也就不会显著地对横向振动产生影响.
2)对于变结构刚度箔片,转子的轴向位移和水平位移趋于稳定的计算时间分别需要0.2s和1.5s.轴向冲击时,轴向位移的峰值达到450μm,0.15s后又趋于零;对于恒定结构刚度箔片,转子的轴向位移和水平位移趋于稳定的计算时间分别需要0.2s和0.15s,轴向冲击时,轴向位移的峰值达到1000μm,0.12s后又趋于零.
3)对于变结构刚度箔片,随着位移增大,箔片越硬,等效刚度越大,因此转子振幅会减小,但是等效阻尼会减小,所以转子振荡时间会略长.因此在设计时,要注意箔片结构刚度和结构阻尼的合理匹配,以保证转子在轴向冲击下的轴向震荡时间和振幅均不超过允许值.
4)永磁体的负刚度绝对值越大,轴向振幅越大,当永磁体的负刚度绝对值过大时,推力盘会撞到箔片轴承.因此在设计箔片轴承-盘式永磁电机转子系统时,需要综合考虑永磁轴承刚度和箔片轴承刚度,以及阻尼之间的匹配.
