滚动轴承的刚度分析方法与试验测定*
2018-03-14任红军
任红军
(辽宁科技大学 机械工程与自动化学院, 鞍山 114051)
引言
滚动轴承的刚度分析是进行轴承设计与优化的基础,对于分析滚动轴承-转子系统的动力学特性具有重要意义,主要涉及滚动体与滚道间的弹性接触问题和轴承整体变形与平衡问题.面向工程设计需求,如何方便有效地确定轴承刚度十分重要.
Stribeck[1]首先通过大量试验对钢球及滚道的弹、塑性接触问题进行了研究,确定球轴承的许用接触载荷,给出了球轴承在径向外载荷作用下滚动体最大接触载荷的经验计算公式.Sjovall[2]和Lundberg[3]进行了径向、轴向载荷以及弯矩载荷的滚动轴承滚动体变形与载荷分布规律研究,给出了滚动轴承在联合载荷作用下的套圈位移及载荷分布的计算方法.此外,目前有限元方法广泛应用于滚动轴承刚度分析中,包括计算轴承刚度[4]、接触应力[5,6]、变形[7],有限元模型中可以考虑轴承、轴以及轴承支承结构[8,9].采用有限元法对轴承组件整体分析,存在节点数量与计算精度的矛盾,一般情况下计算量大且费时.对于高速运行下的滚动体等零件惯性力影响,其计算精度更不能满足.
Jones[10]假定滚动体与滚道之间的切向接触问题符合Coulomb摩擦定律,并采用滚道控制理论作为滚动体的运动边界条件.Jedrzejewski和Kwasny[11]考虑滚动体离心力、陀螺力矩对接触角影响,建立角接触球轴承力学模型,分析了离心力和陀螺力矩效应对轴承刚度及变形的影响.Noel等[12]在Jones模型基础上提出五自由度角接触球轴承刚度矩阵计算方法.Yi等[13]研究不同轴向预紧力、转速条件下角接触球轴承刚度,并通过试验测量内圈、外圈的位移验证模型准确性.赵春江等[14]研究高速条件下角接触球轴承钢球的陀螺力矩和外部负载以及摩擦系数的关系.
本文基于Hertz接触理论,系统给出了滚动轴承力学模型的建立方法,获得滚动轴承五自由度刚度模型的解析表达式,为滚动轴承的动力学分析与优化设计奠定基础.
1 滚动轴承的力学分析
滚动轴承的力学模型如图1所示,在该模型中,不计轴承的质量,轴承座及其基础视为刚性,轴承外圈全约束固定,内圈与转轴过盈配合.建立固定坐标系为OXYZ,其坐标原点O为固定点,位于滚动轴承外圈中心点处,X为轴向坐标,Y、Z为径向坐标.作用在滚动轴承上的外载荷和相应的滚动轴承的弹性变形分别为:
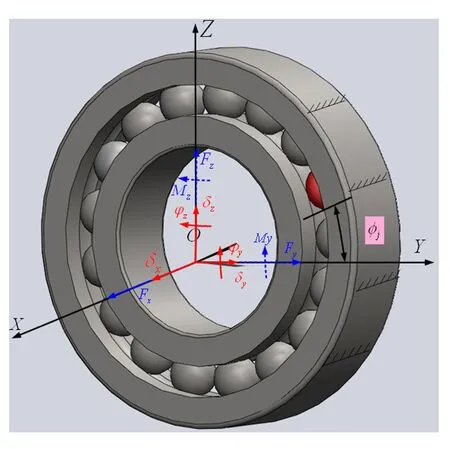
图1 滚动轴承简化力学模型示意图Fig.1 Simplified mechanical model of rolling bearing
假设滚动轴承共有m个滚动体(在这里指滚珠个数).每个滚珠与内外圈接触并相互作用,存在力平衡关系.其力学模型如图2所示.
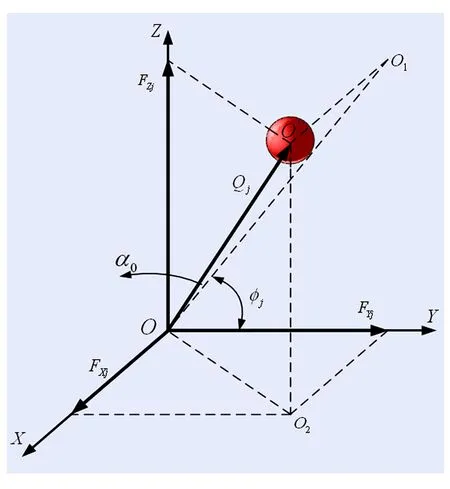
图2 单个滚珠受力学模型图Fig.2 Mechanical model of one ball
设滚珠与内外圈的接触满足Hertz接触应力理论,第j个滚珠对轴承内圈沿法线方向的接触力Qj与其变形δj之间的关系为:
(1)
其中,Kn为滚珠与内外圈之间总的载荷-变形系数(单位N/mn),n是接触指数,对于滚珠轴承可以设为n=1.5.
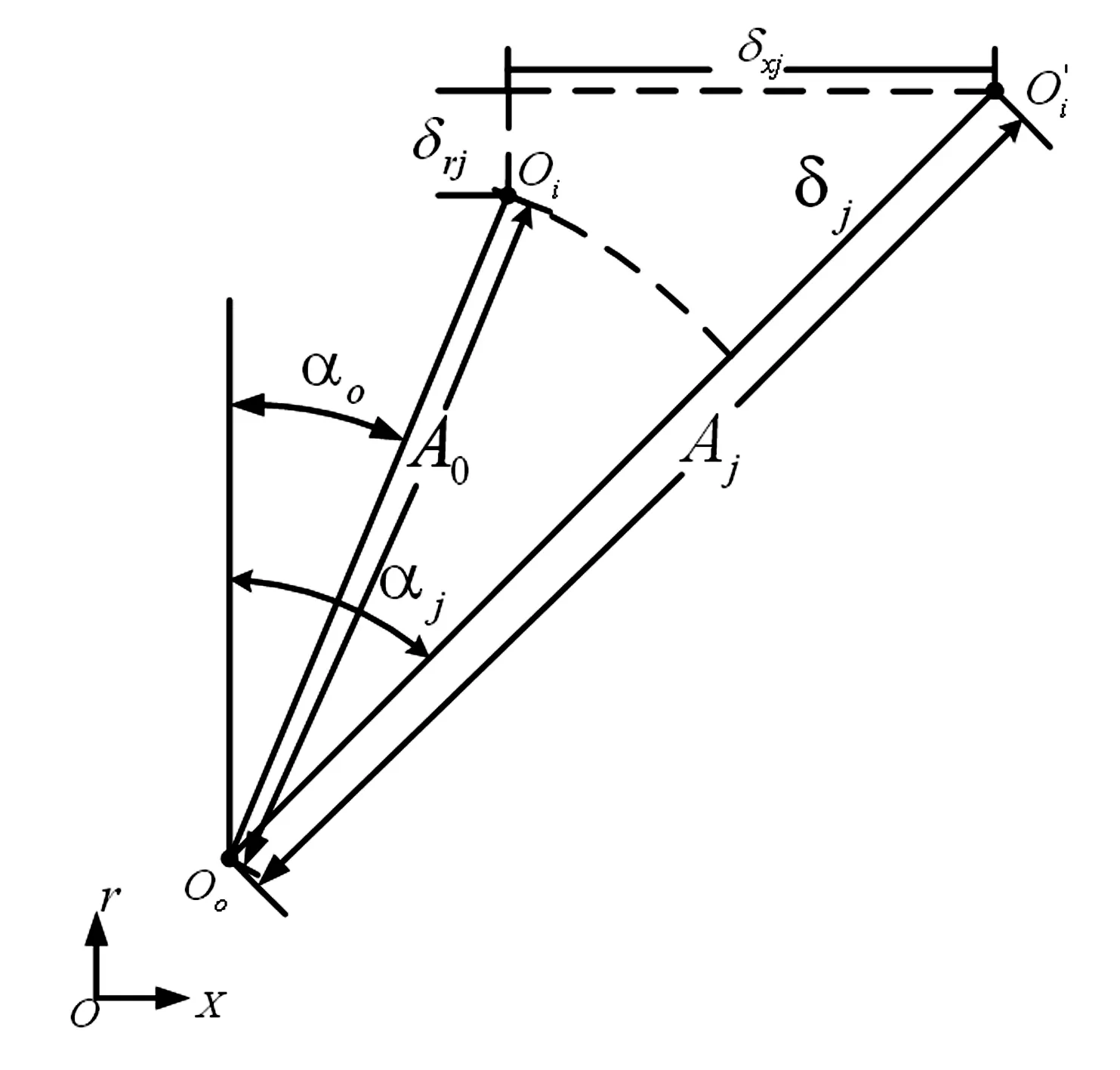
图3 滚珠与内外圈的相对变形示意图Fig.3 Relative deformation of inner and outer raceway and ball
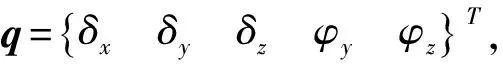
δxj=δx+Rj(φysinφj-φzcosφj)
(2)
δrj=δycosφj+δzsinφj
(3)
其中,Rj为内滚道沟曲率中心轨迹半径,φj为第j个滚珠的位置角.
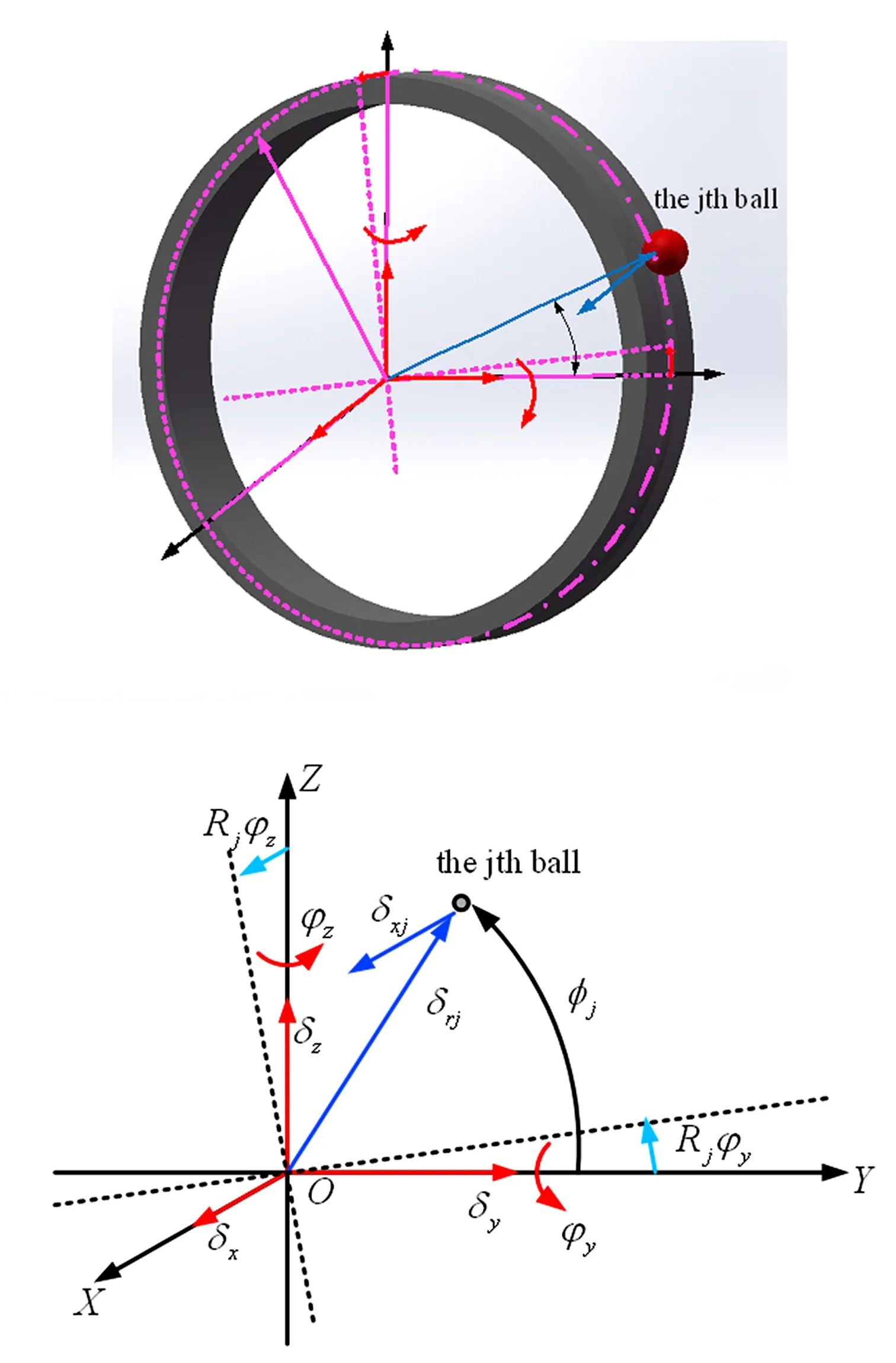
图4 第j个滚珠与内外圈的相对变形示意图Fig.4 Inner and outer raceway andjth ball deformation
式(1)中的滚珠与内外圈之间总载荷-变形系数Kn,是由内圈和外圈的载荷-变形系数Ki、Ko综合求得,即:
(4)
其中,滚珠内圈和外圈的载荷-变形系数Ki、Ko的计算式为
(5)
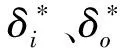
这样,在得到式(1)中的一个滚珠与内外圈之间的载荷-变形系数Kn和接触变形量δj后,即可得到其弹性接触作用力Qj.
2 滚动轴承刚度矩阵的推导
滚动轴承的整体载荷-位移关系具有如下关系.即将上面得到的任意位置角φj处的任一滚珠j的弹性接触作用力Qj按轴承总体5个自由度方向进行分解,得:
Fxj=Qjsinαj
Fyj=Qjcosαjcosφj
Fzj=Qjcosαjsinφj
Myj=RjQjsinαjsinφj
Mzj=-RjQjsinαjcosφj
(6)
将轴承所有滚珠的接触力进行求和,再根据滚动轴承内圈的平衡条件, 即作用在轴承上的外力与所有钢球对内圈的作用力平衡,可得如下轴承整体平衡方程:
(7)
在受小载荷作用时,滚珠与套圈之间的接触变形一般是微米级的.在微小变形情况下,滚动轴承各方向上的刚度可近似为线性刚度,即滚动轴承的外载荷与轴承位移之间的关系可记为
F=Kq
(8)
其中K为滚动轴承刚度矩阵,为5×5阶的矩阵,其定义为:
(9)
其中Kij是刚度矩阵元素,是外载荷分量对弹性位移分量的偏导数.若忽略交叉刚度,只考虑5个方向的主刚度,滚动轴承刚度矩阵K可记为:
(10)
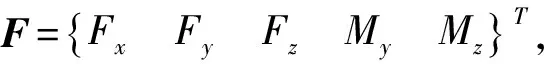
3 结果与分析
3.1 轴承参数
以71807AC角接触球轴承为例加以分析,所采用轴承的内外圈及滚动体所采用的材料均为GCr15轴承钢,轴承基本参数如表1所示.
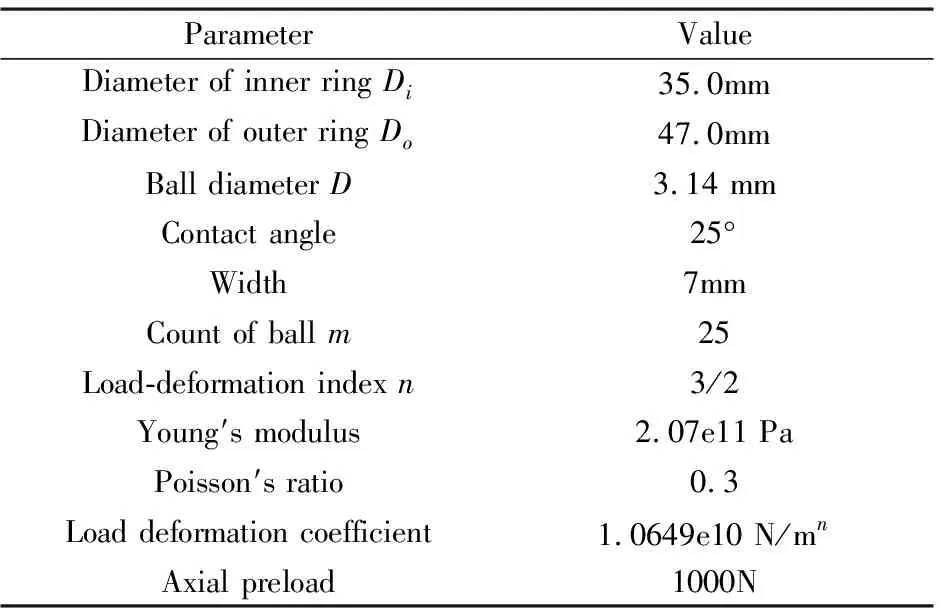
表1 71807AC角接触球轴承基本参数Table 1 Basic parameters of angular contact ball bearings 71807AC
3.2 轴承刚度测试
滚动轴承刚度测试试验台如图5所示.被测滚动轴承安装在轴上,其内圈与轴过盈配合,外圈固定在轴承支座上.加载装置分别位于轴向和径向两个方向上,通过力传感器数显装置读取施加的载荷大小,数显千分表分别位于滚动轴承左端轴向方向和靠近轴承的转轴水平方向,用以近似轴承的轴向和径向位移.

图5 滚动轴承性能测试原理性试验器Fig.5 Test rig for performances of ball bearing
3.3 测试结果对比分析
将试验结果与仿真分析的计算结果进行比较.图6表示了不同轴向负荷作用下,轴承的轴向变形情况.
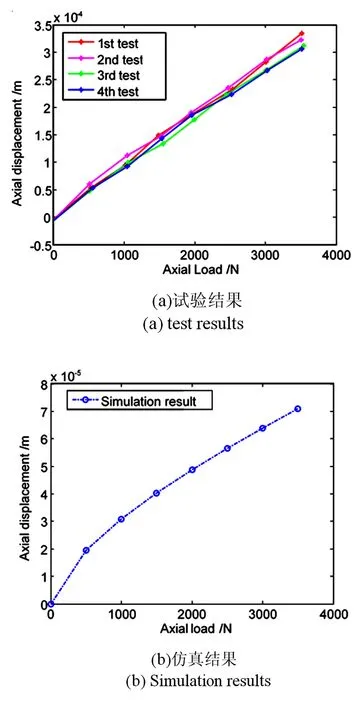
图6 不同轴向载荷作用下轴承的轴向位移Fig.6 Axial displacement of ball bearing vs. axial preload
由图6可以看出,试验具有很好的重复性,四次测试的结果基本一致.此外,仿真分析结果与试验测试结果在趋势上表现出一致性.
轴承轴向测试刚度和仿真计算的轴承轴向刚度比较如图7所示.
由图7可以看出,在给定的轴向载荷范围内(500~3500N),试验所得的轴承轴向刚度出现波动,仿真分析结果随着轴向载荷的增大而增大.测试所得轴向刚度较小,由于考虑了试验装置中轴、轴承座和轴承的串联后的刚度.
在固定的轴向预载(2800N)条件下,不同径向载荷作用下,轴承的径向位移变化规律和径向刚度变化,分别如图8和9所示.
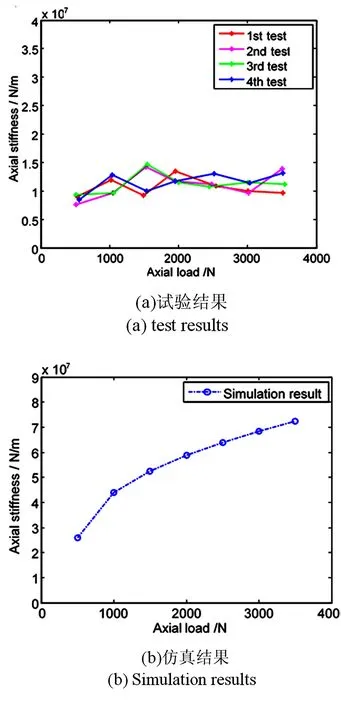
图7 不同轴向载荷作用下轴承的轴向刚度Fig.7 Axial stiffness of ball bearing vs. axial preload
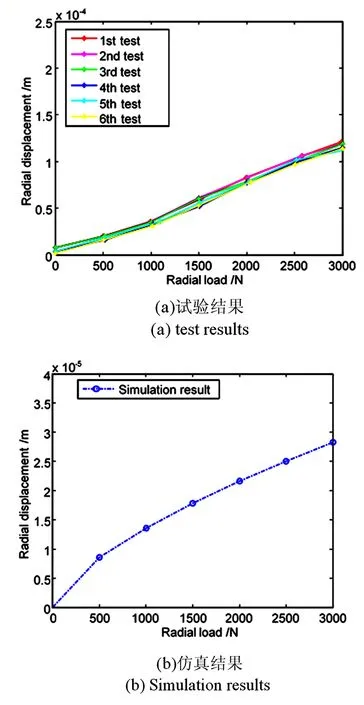
图8 不同径向载荷作用下轴承径向位移Fig.8 Radial displacement of ball bearing vs. radial preload
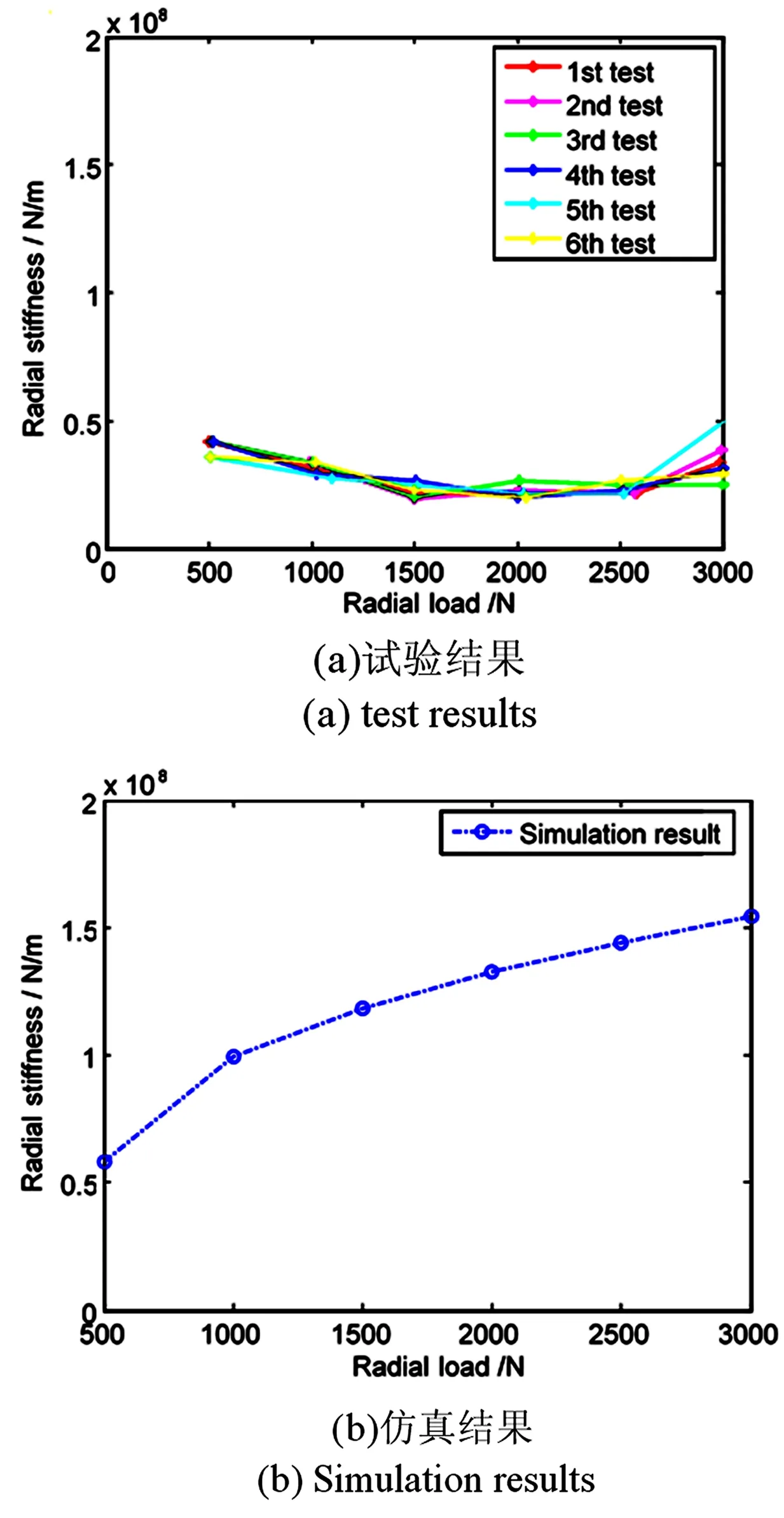
图9 不同径向载荷作用下轴承径向刚度Fig.9 Radialstiffness of ball bearing vs. radial preload
由图8可以看出,试验具有良好的重复性,六次测试的结果基本一致.此外,仿真分析结果与试验测试结果在趋势上表现出一致性,随着径向载荷的增大,径向位移均呈线性增大趋势.
由图9可以看出,在给定的径向载荷范围内(500~3000N),试验所得的轴承径向刚度呈现先减小后增大的趋势,仿真分析结果随着轴向载荷的增大而增大.试验测试所得轴承刚度较小,由于该刚度为考虑了试验装置中轴、轴承座和轴承的串联后的综合刚度.该试验测试结果与仿真分析结果在整体趋势上表现出了相似性,一定程度上验证了仿真计算模型的有效性.
4 结论
(1)本文给出了小变形下,基于Hertz接触理论滚动轴承五自由度刚度矩阵的计算方法;
(2)轴承内圈位移整体上随着载荷的增大而呈线性增大;
(3)利用刚度模型获得的理论分析结果与试验测试结果在趋势上表现出良好的一致性.
