FMCW雷达周期非线性相位估计与矫正

李公全, 赖 涛, 靳 科, 赵拥军

(信息工程大学导航与空天目标工程学院, 河南 郑州 450001)

0 引 言

调频连续波(frequency modulated continuous wave,FMCW)雷达相对脉冲体制雷达具有体积小重量轻,结构简单,成本低,低截获概率等优点,因此FMCW雷达在近距离安全检测、机场异物识别、形变测量等领域具有广泛的应用[1-4]。而FMCW雷达发射信号的非线性失真严重制约其性能,尤其在解线频调接收机制下,FMCW信号的非线性问题使目标回波能量大范围扩散,严重恶化距离分辨率[5],并且信号回波的时延越大,非线性误差对系统的影响越大。

由于硬件矫正电路稳定性差,调试周期长,因此信号处理矫正方法凭借其通用性、移植性强的特点以及矫正精度高的优势,得到研究者的青睐。通常可以将非线性相位建模为多项式相位、周期相位、随机相位三类,实际雷达系统中这3类相位均存在,只是比重各有差异。针对多项式相位误差的矫正,文献[6]采用高阶模糊函数(high-order ambiguity function, HAF)估计多项式系数,然后利用重采样方法对非线性误差进行矫正,具有较强的工程应用性。文献[7]综合利用匹配信号变换及频谱聚集度实现多项式系数的最大似然估计与非线性矫正,具有良好的抗噪性能,在实际雷达系统中得到了很好的应用。

相比多项式相位,周期相位在非线性相位中处于从属地位。在多项式相位矫正后,距离压缩图像的旁瓣一般都能得到较大程度抑制,但是在汉明加窗距离压缩的情况下(在实际雷达信号处理中非常有必要),由周期非线性引起的成对回波凸显出来,严重影响距离压缩质量。因此为获得更高质量的距离压缩效果,周期相位误差的估计与矫正是非常有必要的。目前,针对周期相位误差矫正的研究还较少,文献[8]对产生周期相位误差的因素进行了分析,比如直接数字式频率合成器(direct digital synthesizer,DDS)本身的杂散、DDS时钟杂散以及供电电压杂散,但并没有提出矫正方法。文献[9]在直接采样条件下对发射信号采用三阶正弦拟合对周期相位进行了矫正,但是在宽带条件下很难实现直接采样,同时估计阶数较低,对周期相位误差补偿效果有限,有较多的残余成对回波无法消除。

随着系统带宽提高,FMCW雷达大多采用Dechirp接收以实现低采样率回波采集,从而使得发射非线性与接收非线性耦合,产生了空变效应,增大了估计以及矫正的难度。本文在宽带FMCW雷达Dechirp接收体制下,把多项式非线性矫正后的剩余非线性相位建模为多周期正弦分量之和,剖析了周期相位误差对距离压缩的影响,着重研究了多分量正弦调频非线性的参数估计以及矫正问题,提出了匹配初值与非线性最小二乘相结合的参数估计方法,将信号相位变换到频域后利用峰值搜索获得调制频率的估计,进而构造匹配函数,通过一维相位搜索同时估计出幅度以及初相,并以此为初值,利用非线性最小二乘进一步提高估计精度,最后利用匹配傅里叶变换(match Fourier transform,MFT)[10]进行空变非线性矫正。在参数初值估计时仅采用了傅里叶变换及一维相位搜索,能够快速获得参数初值的估计结果,克服了多分量正弦参数估计时由于初值选取偏离实际值较大而造成非线性最小二乘难以快速收敛的困难。仿真结果证明了算法的可行性,蒙特卡罗仿真表明随着信噪比提高,参数估计性能逼近克拉美罗下界。对X波段宽带FMCW雷达实测数据的处理结果表明,所提算法能够有效抑制成对回波,显著提高峰值旁瓣比,得到更好的一维距离像压缩效果。

1 差频信号相位误差分析

1.1 差频信号模型

存在非线性误差的FMCW发射信号可以写为

(1)

式中,fc为载波频率;K为调频率;ε(t)为调频非线性误差项。

经过一定时延之后,理想点目标的接收信号为

(2)

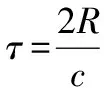
则Dechirp接收之后信号形式变为

(3)

式中,相位第2项包含了目标的距离信息,通过傅里叶变换可以在频谱上进行精确估计；第3项为残余时频相位项(residual video phase, RVP)[11]。在近场成像时,时延很小,RVP项可以忽略,同时误差可以近似为导数与时延的乘积,此时中频信号可以写为

sif(t)=exp{j2π[fcτ+Ktτ+ε′(t)τ]}

(4)

因此，差频信号的相位误差与目标和雷达之间的距离有关,即误差存在空变性。

根据HAF矫正算法[6],可以将误差信号建模为多项式集合:

(5)

式中,L为多项式阶数,通常取5～7阶。

则中频信号可以进一步表示为

(6)

式中,α1=K。

经过HAF算法矫正之后的信号去除了多项式相位误差,但是仍然可能存在周期误差分量,造成主瓣两边对称的成对回波,第3.2节的实测数据处理也验证了这种观点,对剩余误差做FFT时可以看到存在若干尖峰。

下面将从匹配滤波脉冲压缩的角度进行更深入地讨论和研究周期相位误差对一维距离像的影响。

1.2 周期相位误差的特性及影响

为方便分析,假定周期相位误差为单频正弦信号,则中频信号可以表示为

sif(t)=exp{j2π[fcτ+Ktτ+Aeτsin(2πfet+θe)]}

(7)

式中,Ae单频正弦相位误差的幅度;fe为单频正弦相位误差的频率;θe为单频正弦相位误差的初相。

假设理想的FMCW信号通过匹配滤波器后的输出信号为so(t),则存在单频周期失真时,匹配滤波后的输出信号[12]为

som(t)=J0(Aeτ)Env[so(t)]·cos(2πfct)+

cos[(2πfc+nπfe)t+nθe]+

(8)

式中,Jn(Aeτ)为n阶第一类贝塞尔函数;Env(·) 为取信号包络。

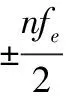
cos[(2πfc-πfe)t-θe]}

(9)

而实际场景中周期相位误差为多个正弦信号之和,即

(10)

这时,成对回波不再仅仅是上述简单情况的叠加,而且还应加上相互作用的交叉项。但是,由于高次项往往很小,故在很多场合可以忽略不计,此时前面的分析结果依然适用。匹配滤波输出端的成对回波相当于压缩波形的旁瓣,会降低峰值旁瓣比,对于合成孔径雷达(synthetic aperture radar, SAR)来说将造成虚假目标,同时造成成像时的鬼影,因此非常有必要对周期相位误差信号进行估计与矫正。

2 周期相位误差的估计与矫正

在实际处理时,由于延迟线数据最为纯净,更能反映系统的非线性,在进行系统参数估计时也更加准确,因此首先使用延迟线数据对系统周期相位误差各参数进行估计。

由以上分析可知,能够将差频信号的相位误差进一步建模为多项式相位集合与正弦函数集合的和，即

sif(t)=exp{j2π[fcτref+Ktτref+

(11)

式中,M为正弦周期相位的阶数;τref为延迟线时延。

去除多项式相位之后剩余信号

(12)

取此时信号的相位并解缠绕:

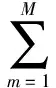
(13)

为了简化,式(13)可以进一步写为

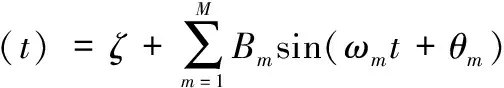
(14)

式中,Bm=2πAmτref；ζ=2πfcτref。需要说明的是,由于延迟线时延τref不准确,ζ为一未知数,但可以将ζ看作常数,并不会影响后续正弦参数的估计。

非线性最小二乘参数估计是当前应用较广泛的参数估计算法[13],可以有效解决本文模型中的参数估计问题,但是参数初值的选取将直接影响最小二乘的收敛速度以及陷入局部最优解的概率。在多阶周期误差信号的参数估计上,需要估计的参数数量很大,因此在参数初值的选取上不能够随意指定。

2.1 基于频率相位匹配的参数初值估计

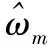
(15)

式中,θ∈(-π,π),为待估计相位。

将匹配函数与误差信号相乘,即

χm(t)=φm(t)·γm(t)=

(16)

式中，φj(t)为误差相位;初始为φ1(t)=φ(t)。

令m=m+1,更新误差相位,即

(17)

重复以上步骤,直到估计出M个正弦分量的参数值。

基于频率相位匹配的参数估计方法可以很快速的获得各个正弦分量的幅度,频率以及初相的初步估计值,虽然在估计的过程中存在误差传递以及估计不够准确的问题,但是用其作为非线性最小二乘估计的初值却是十分方便以及快捷的。

2.2 基于非线性最小二乘的多分量正弦信号参数估计

针对粗略估计的参数初值,仍然需要进行更加精确的优化,使估计值更加接近真实值,通过构建优化目标函数,非线性最小二乘算法可以快速完成这一优化过程。

在本模型中,令

φdata(t)

(18)

式中,b=(B1,B2,…,BM);ω=(ω1,ω2,…,ωM);θ=(θ1,θ2,…,θM);φdata(t)为相位数据。

因此,非线性最小二乘目标函数可以表示为

(19)

将式(18)代入式(19)得

φdata(t)]·

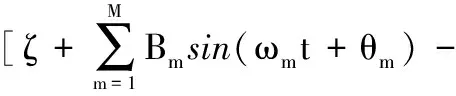
(20)

函数ξ(b,ω,θ)的极值点(b*,ω*,θ*)就是最小二乘解,即

(21)

在非线性最小二乘求解时,可以采用经典的信赖域优化算法[14]。将ξ(b,ω,θ)在当前点(b,ω,θ)(k)处泰勒展开到二次项:

Qk(d)=ξ[(b,ω,θ)(k)]+[g(k)]Td+

(22)

式中,g(k)和Gk分别是ξ(b,ω,θ)在(b,ω,θ)(k)处的梯度向量以及Hesse矩阵;d(k)是Qk(d)的最小点。

信赖域算法的主要思想就是在(b,ω,θ)(k)的邻域内用Qk(d)的极小解近似ξ(b,ω,θ)并令(b,ω,θ)(k+1)=(b,ω,θ)(k)+d(k)作为ξ(b,ω,θ)极小解新的近似不断重复。其中d(k)的求解问题通常叫做信赖域子问题,即解下式:

minQk(d)

s.t. ‖d‖≤hk

(23)

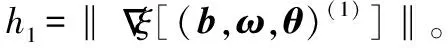
记

(24)

它们的比值

(25)

当ξ(b,ω,θ)为二次函数时rk等于1,对于一般函数,rk越接近于1表示在(b,ω,θ)(k)的这个邻域内Qk(d)近似ξ(b,ω,θ)程度越高,因此以rk作为衡量近似程度的指标。

则信赖域方法的计算步骤如下[15]。

步骤1给定初始值(b,ω,θ)(1),初始半径h1,迭代终止误差μ,令k=1。

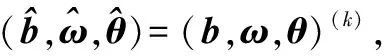
步骤3求式(23)的解,计算ξ[(b,ω,θ)(k)+d(k)]及rk,转步骤4。

步骤4若rk<β1,令hk+1=β2∥d(k)∥;若rk>β3及∥d(k)∥=hk,此时令hk+1=β4hk;否则令hk+1=hk。

步骤5若rk≤0,则令(b,ω,θ)(k+1)=(b,ω,θ)(k);否则令(b,ω,θ)(k+1)=(b,ω,θ)(k)+d(k),k=k+1,转到步骤2。

根据经验,可取信赖域法中参数β1=0.25,β2=0.25,β3=0.75,β4=2。

2.3 非线性矫正MFT算法

MFT[10,16]的一般形式为

(26)

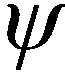
含正弦周期相位误差的多目标差频信号可表示为

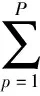
(27)

式中,P为目标数;τp为第p个目标的回波时延。

其傅里叶变换为

(28)

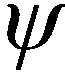
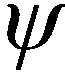
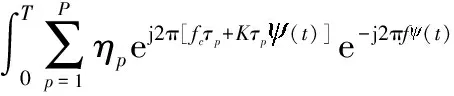
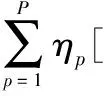
(29)

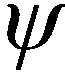
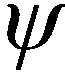
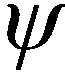
(30)

可见,虽然估计出的Bm含有延迟τref,但是由文献[6]可知,在进行多项式系数估计时,Kτref作为一个整体被估计出来,因此在实际进行周期误差矫正时τref被消除掉,即式(30)与τref值无关,并不需要知道系统延迟线τref的精确值。

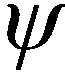
综上,整个非线性矫正的流程如图1所示。

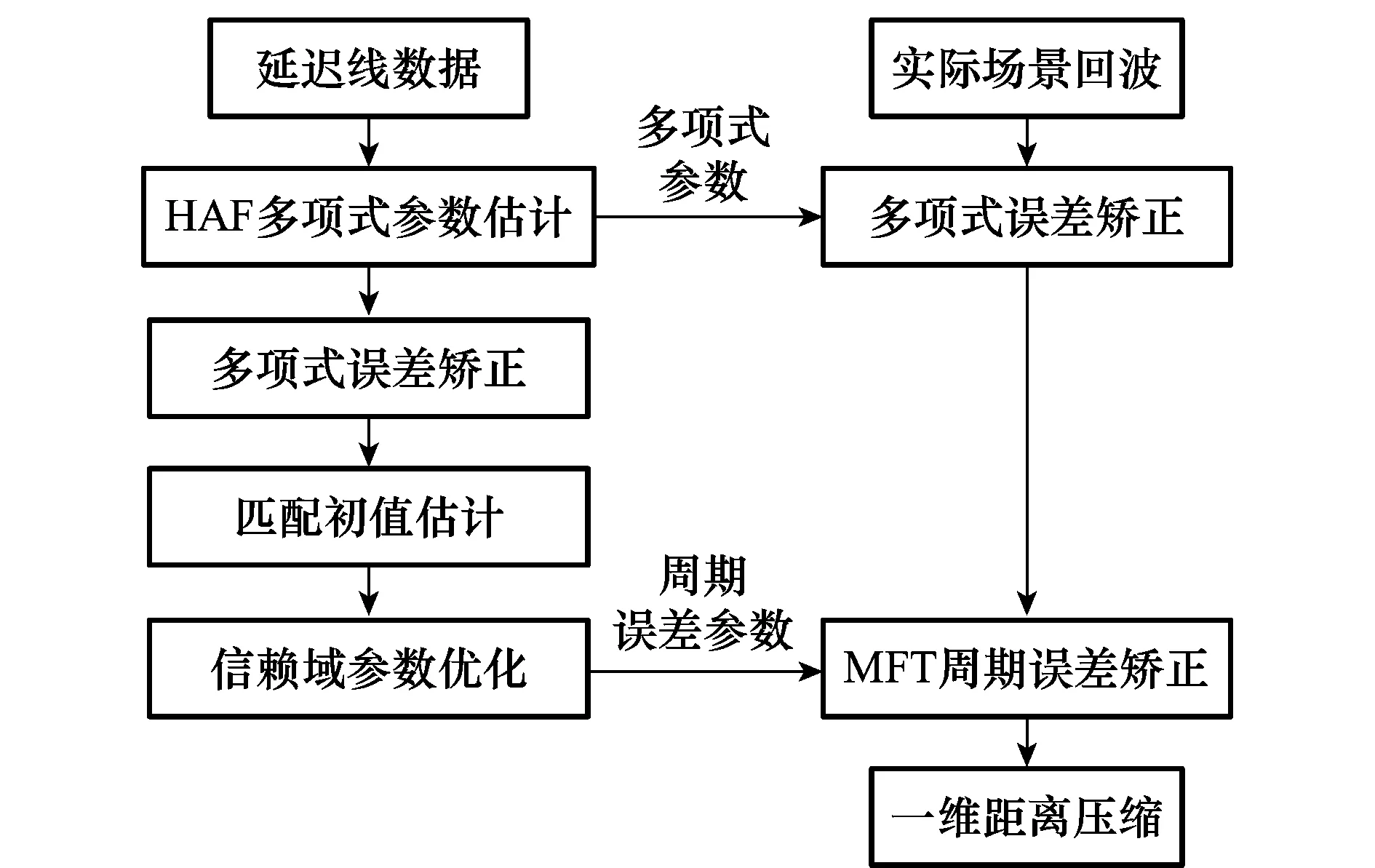
图1 非线性矫正流程Fig.1 Nonlinearity correction process

3 仿真实测验证

为验证算法的有效性,进行了仿真以及实测数据验证。本节主要包含两部分,第一部分进行含周期相位误差信号的单目标以及多目标一维距离向成像,同时对不同信噪比下算法的估计性能进行了仿真分析;第二部分对实际系统的延迟线以及角反射器数据进行周期误差的非线性矫正,显示算法在实际系统中的应用效果,证明了算法的工程实用性。

3.1 仿真验证

根据实际系统的参数,设置了仿真模拟的系统参数如表1所示。

首先,对10 m处的模拟点目标进行仿真矫正。系统采用三阶周期相位误差,矫正前后的一维距离像结果如图2所示。从图中可以看出,周期相位调制并不会影响系统的分辨率,但是在旁瓣结构上会出现严重的成对回波,降低了峰值旁瓣比,将会掩盖对远区弱目标的探测。经过对周期相位误差的矫正,旁瓣电平由-20 dB降低到约-39 dB,接近理想情况。

表1 宽带FMCW雷达系统参数

然后,将估计出的参数对位于15 m以及16 m的两个点目标进行矫正,矫正前后结果如图所示,可以看到与单个点目标的旁瓣抑制效果基本一致。

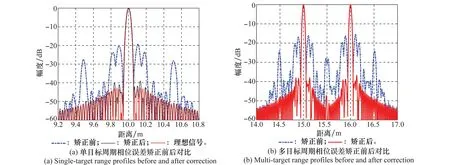
图2 非线性矫正仿真结果Fig.2 Simulation results of nonlinearity correction

上述仿真是在理想环境下进行的,为了评估算法的普适性,我们对不同信噪比条件下的估计性能进行了蒙特卡罗数值仿真。

文献[17]已经给出了正弦调频幅度和频率CRLB的详细推导过程,在此基础上进一步推导出初相的CRLB,鉴于推导过程基本类似且篇幅较长,在此只给出推导结果为

(31)

式中,N为信号长度。

由于多分量正弦调制相位的参数估计与单分量参数估计在估计性能上没有本质区别,只是计算复杂度更高一些,因此为方便起见,我们对只单分量正弦调制相位的参数估计性能进行分析即可。信噪比从5 dB到20 dB变化,采用100次蒙特卡罗数值仿真实验,分别计算调制相位的幅度,频率以及初相的归一化均方根误差(normalized mean square error, NRMSE),图3显示出本算法的估计性能。

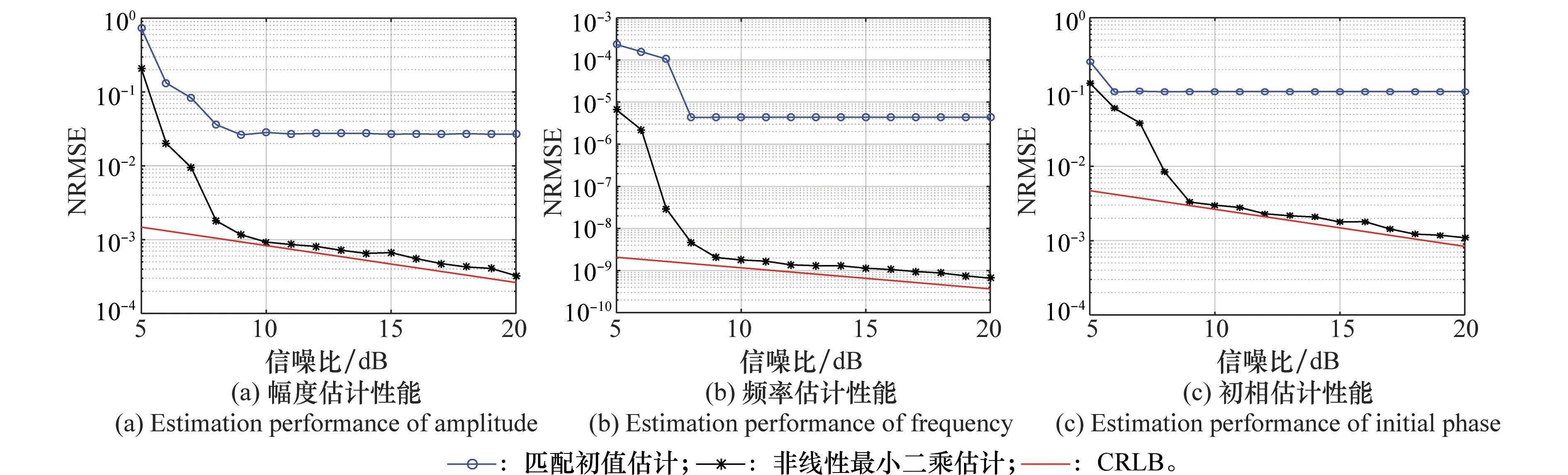
图3 调频参数估计性能分析Fig.3 Estimation performance analysis

由图3可知,由于匹配初值估计是基于频谱的估计,因此受限于频率间隔以及相位搜索的步长,非线性最小二乘显著提高了参数估计精度。由于本算法是基于取相位的参数估计,因此存在8 dB的信噪比门限,但是在信噪比大于8 dB时本算法估计参数的NRMSE逼近CRLB。

3.2 实测数据验证

为了体现本算法的实际应用效果,我们利用实验室研制的超宽带FMCW雷达系统实测数据进行验证,雷达参数如表1所示,系统结构框图可参考文献[18]。首先根据系统延迟线数据对系统的周期相位误差参数进行估计,然后再对实际场景的回波进行矫正。因此在本算法应用时,只需在原系统上加装一条延迟线即可,并不会过多增加系统的复杂性。系统实景测试如图4所示。

图4 实测场景图Fig.4 Field survey scenario

根据算法的具体实现过程,通过约3 m的延迟线回波数据对相位误差参数进行了估计,之后对位于约4.93 m的角反射器回波数据进行矫正。首先用高阶模糊函数法矫正信号中多项式非线性相位的影响,在回波没有加Hamming窗时,看似信号达到了我们所需求,如图5(a)所示;但是加入Hamming窗后,主瓣两旁的成对回波凸显出来,且峰值旁瓣比仅有21 dB,如图5(b)所示,这些成对回波对周围目标有很强的掩盖效应,远远不能满足我们对信号检测的要求,因此迫切需要矫正这些周期性相位误差。对多项式相位矫正之后的残余相位误差做傅里叶变换以观察其频谱,如图5(c)所示,从中可以看出残余相位频谱中具有明显的周期性相位误差,表现出多个尖峰,这种情况下仅如文献[9]采用3阶正弦函数拟合是不够的。

应用本文算法对多项式相位矫正之后的数据继续矫正,图6分别为延迟线与角反射器回波矫正结果。从图5(c)的残差频谱图中粗略看到了7个频率谱峰,在实际处理时,为显示更多细节频率成分以及降低因某个频率估计不准造成非线性最小二乘优化过程收敛较慢,同时兼顾数据处理的运算效率,在本文中采用9阶正弦对延迟线回波数据中的周期相位误差进行估计。同时,由于系统稳定性良好,在实际参数估计时,只需根据一个延迟线脉冲数据对参数进行估计即可对其他脉冲或者其他场景回波数据进行矫正。

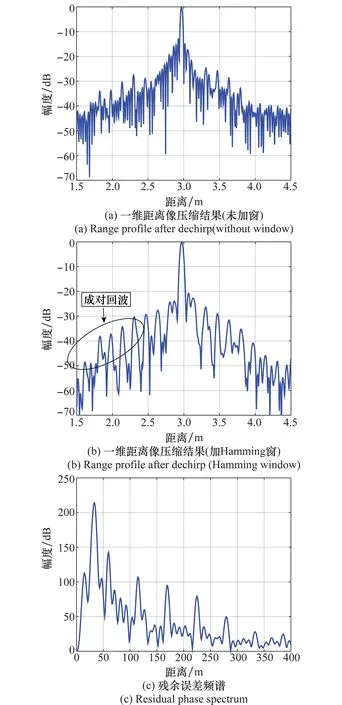
图5 多项式误差矫正结果Fig.5 Results of polynomial nonlinearity correction

从图6中可以看出,算法在多项式矫正结果的基础上仍然能够将延迟线数据一维距离像旁瓣压缩9 dB左右,显著抑制了成对回波,同时矫正后距离分辨率为3.85 cm,接近3.82 cm的理想分辨率。由于实际场景的复杂性,对角反射器数据的矫正结果虽然不如延迟线数据的矫正结果优越,但仍能将旁瓣抑制7～8 dB,距离分辨率也得到了较大改善,能够有效提升对目标的检测与成像效果,显示了本算法良好的工程应用性。延迟线和角反射器矫正前后详细指标如表2所示。

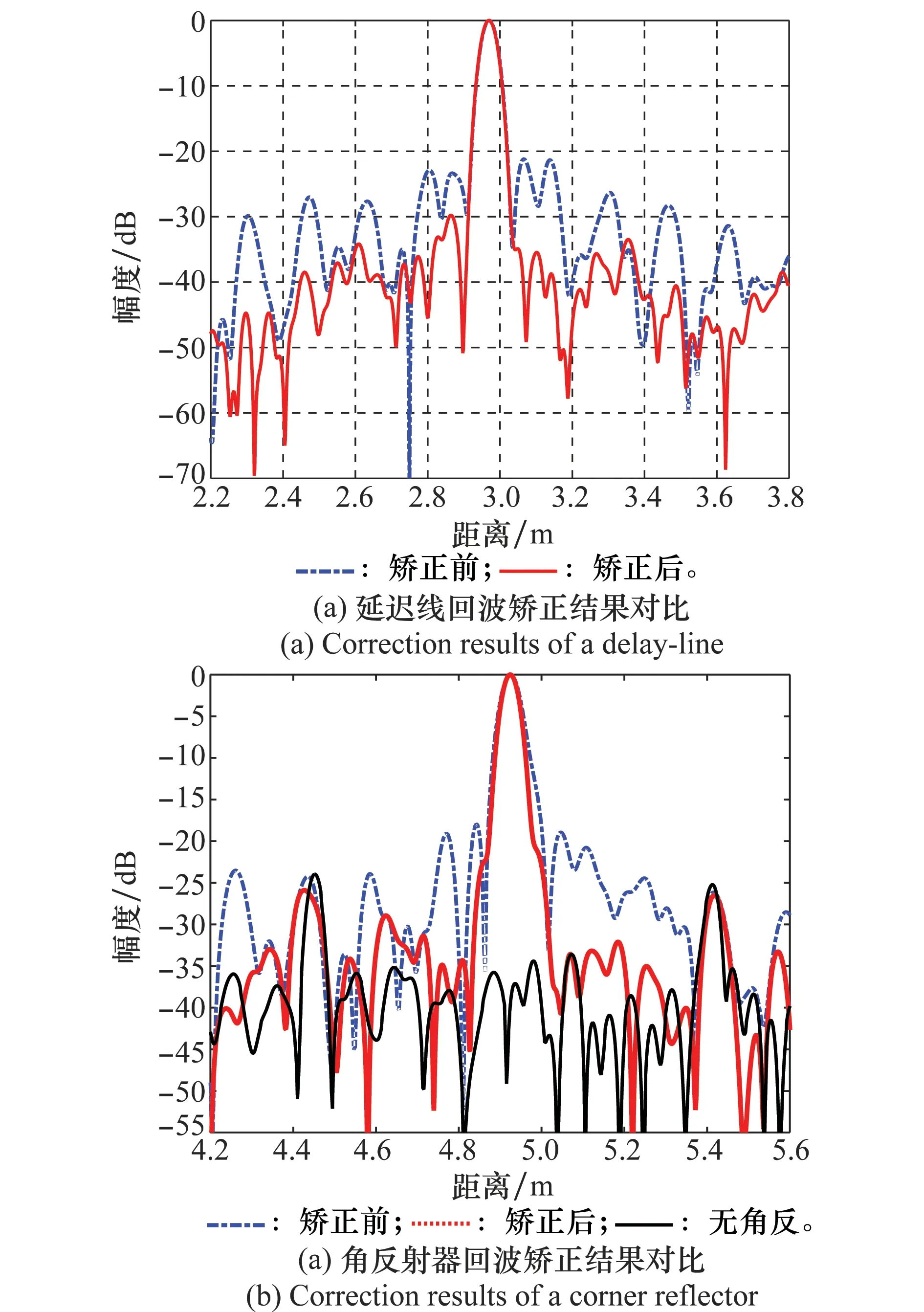
图6 实测数据周期相位误差矫正结果对比Fig.6 Field survey results of nonlinearity correction

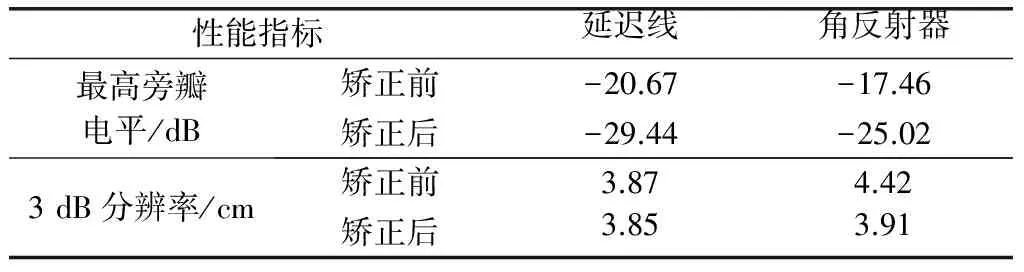
性能指标延迟线角反射器最高旁瓣电平/dB矫正前-20．67-17．46矫正后-29．44-25．023dB分辨率/cm矫正前3．874．42矫正后3．853．91

但是,从图6(b)也可以看出,虽然近处旁瓣得到了较好的抑制,但是仍然存在没有估计消除的远区旁瓣。这一点解释为地板下可能存在的强散射体,图中黑色实线是无角反射器存在时对环境的成像结果,在约4.45 m以及5.40 m的位置同样出现较强的反射,从侧面验证了上述结论。当然,在实际应用中,鉴于正弦估计的阶数有限,也可能产生类似的远区旁瓣。

4 结 论

本文主要研究了FMCW信号周期非线性误差的参数估计与矫正问题。文章首先分析了距离压缩中由周期非线性误差引起的成对回波现象,然后针对周期相位误差的参数估计问题,采用频率相位匹配对参数的初值进行估计,之后为提高参数估计性能,采用了信赖域算法对估计出的初值进行优化,最后通过MFT对误差进行矫正。仿真以及实测数据均表明本文算法能够准确估计周期相位误差参数,显著抑制成对回波效应,提高对目标的检测和成像效果,具有良好的工程应用性。

[1] POHL N, JAESCHKE T, VOGT M. Ultra high resolution SAR imaging using an 80 GHz FMCW-radar with 25 GHz bandwidth[C]∥Proc.of the European Conference on Synthetic Aperture Radar, 2012:189-192.

[2] IGLESIAS R, AGUASCA A, FABREGAS X, et al. Ground-based polarimetric SAR interferometry for the monitoring of terrain displacement phenomena-Part I: theoretical description[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(3):980-993.

[3] MOLCHANOV P, GUPTA S, KIM K, et al. Short-range FMCW monopulse radar for hand-gesture sensing[C]∥Proc.of the IEEE Radar Conference, 2015:1491-1496.

[4] YAN J B, ALVESTEGUI G G, MCDANIEL J W, et al. Ultrawideband FMCW radar for airborne measurements of snow over sea ice and land[J]. IEEE Trans.on Geoscience & Remote Sensing, 2016, PP(99):1-10.

[5] WANG Y, LI Q, GAN D, et al. Research on nonlinearity correction imaging algorithm of FMCW SAR[C]∥Proc.of the International Conference on Signal Processing Systems, 2010:V1-425-V1-429.

[6] ANGHEL A, VASILE G, CACOVEANU R, et al. Short-range wideband FMCW radar for millimetric displacement measurements[J].IEEE Trans.on Geoscience & Remote Sensing, 2014, 52(9):5633-5642.

[7] ANGHEL A, VASILE G, CACOVEANU R, et al. Range autofocusing for FMCW radars using time warping and a spectral concentration measure[C]∥Proc.of the IEEE Radar Conference, 2015:0581-0586.

[8] AYHAN S, SCHERR S, BHUTANI A, et al. Impact of frequency ramp nonlinearity, phase noise, and SNR on FMCW radar accuracy[J]. IEEE Trans.on Microwave Theory & Techniques, 2016, 64(10):1-12.

[9] 赵志勇, 常文革, 黎向阳,等. 去调频处理中空变相位误差补偿方法[J]. 国防科技大学学报, 2014(3):169-176.

ZHAO Z Y, CHANG W G, LI X Y, et al. Range-dependent phase error compensation of dechirp[J].Journal of National University of Defense Technology, 2014(3):169-176.

[10] 王盛利, 李士国, 倪晋麟,等. 一种新的变换——匹配傅里叶变换[J]. 电子学报, 2001, 29(3):403-405.

WANG S L, LI S G, NI J L, et al. A new transform—match Fourier transform[J]. Acta Electronica Sinica, 2001, 29(3): 403-405.

[11] MITTERMAYER J, MOREIRA A, LOFFELD O. Spotlight SAR data processing using the frequency scaling algorithm[J]. IEEE Trans.on Geoscience & Remote Sensing, 1999, 37(5):2198-2214.

[12] HU S. Performance analysis of frequency sweep nonlinearities in LFM radars[C]∥Proc.of the IEEE International Conference on Electrical and Control Engineering,2010:3977-3980.

[13] ANGEBY J. Estimating signal parameters using the nonlinear instantaneous least squares approach[M]. IEEE Press, 2000.

[14] 赖炎连,贺国平.最优化方法[M].北京:清华大学出版社,2008.

LAI Y L, HE G P. Optimization methods[M]. Beijing:Tsinghua University Press, 2008.

[15] 谢政, 李建平, 陈挚. 非线性最优化理论与方法[M]. 北京:高等教育出版社, 2010: 194-199.

XIE Z, LI J P, CHEN Z.Nonlinear optimization theory and methods[M].Beijing:Higher Education Press,2010:194-199.

[16] CHEN J J, CHEN J, WANG S L. Detection of ultra-high speed moving target based on matched Fourier transform[C]∥Proc.of the IEEE International Conference on Radar, 2006:1-4.

[17] 霍凯, 游鹏, 姜卫东,等. 正弦调制相位信号参数估计的克拉美-罗下限[J]. 信号处理, 2009, 25(9):1342-1346.

HUO K,YOU P,JIANG W D, et al. The Cramer-Rao lower bound for parameters estimation of signals with sinusoid modulated phase[J]. Signal Processing, 2009, 25(9):1342-1346.

[18] 靳科, 赖涛, 李公全,等. 近距离超宽带调频连续波雷达非线性校正研究[J]. 信号处理, 2017,33(2):158-167.

JIN K, LAI T, LI G Q, et al. Nonlinearity correction of short range wideband FMCW radar[J]. Signal Processing,2017,33(2):158-167.