基于标签随机有限集滤波器的多扩展目标跟踪算法

曹 倬, 冯新喜, 蒲 磊, 王 雪, 张琳琳

(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 空军大连通信士官学校基础部计算机应用教研室, 辽宁 大连 116600)

0 引 言

目标跟踪过程是依据最佳估计原理,采用滤波算法对传感器接收到的量测进行处理,估计目标各状态要素的数据处理过程[1]。在传统多目标跟踪理论中,假设每个目标最多产生一个量测,杂波环境下传感器还会有漏检、虚警等情况的发生[2]。随着现代高分传感器的广泛应用,当跟踪大型目标或者近距离目标时,传感器可对目标提供多个量测值,称之为扩展目标[3-4]。由于扩展目标建模放宽对量测形态的限定,因此更加贴近实际。基于数据关联的滤波方法如果运用于扩展目标跟踪,将出现维数灾难,导致求解困难。随机集理论[5]简化了集合中各元素的关联关系,开辟了目标跟踪领域新的研究方向。基于一阶矩近似的概率假设密度(probability hypothesis density, PHD)滤波器[6]采用单个参数传递势信息,并假设量测数目服从泊松分布,使得该算法对势估计偏差较大。为此,文献[7]在独立同分布假设下提出势概率假设密度(cardinalized probability hypothesis density, CPHD)滤波器,同时迭代目标的势分布和一阶矩,改善了原算法势估计性能,然而状态提取步骤中采用聚类算法可能导致不稳定的状态估计。之后,文献[8]利用多伯努利参数近似目标概率密度,提出了多目标多伯努利滤波器(multi-target multi-Bernoulli, MeMBer)。然而现代战场感知环境和被感知目标特性日趋复杂多变,上述算法在低信噪比感知场景中难以维持较好的跟踪性能,算法输出亦为离散、无序的状态估计集合,无法形成目标有效航迹。为此,文献[9-10]结合数据关联中多假设跟踪(multiple hypothesis tracking, MHT)思想和标签随机有限集(random finite set, RFS)统计理论,提出了广义标签多伯努利(generalised labeled multi-bernoulli, GLMB)滤波器。

扩展目标由质心运动学状态和扩展形态共同表征,由于目标的扩展形态与运动学状态之间存在较强耦合关系,在扩展目标滤波框架中加入扩展形态要素,不仅可以刻画目标的轮廓特征,还将有效提高势估计和目标运动学状态估计的精度。文献[11]首先提出用椭圆定义目标扩展形态,然而该算法对外形估计效果起伏较大。此后,学者利用对称正定随机矩阵表征扩展形态[12-13],得到了简明形态与状态的贝叶斯估计,然而,对称正定矩阵仅能描述单一椭形目标,为此文献[14]提出了基于随机矩阵的非椭形目标跟踪框架。文献[15]提出基于随机超曲面模型的星-凸形扩展形态建模方法,可以刻画具有丰富细节轮廓的现实目标。

本文针对低信噪比感知场景下的多扩展目标跟踪问题,提出基于广义标签多伯努利滤波器的多扩展目标跟踪算法(简记为扩展目标—GLMB(extended targe-GLMB, ET-GLMB)),将目标扩展形态转化为扩维状态并建模为星-凸超曲面,推导了预测和更新方程。实验结果表明,所提算法可在低量测率和密集杂波环境下实现良好的跟踪性能,在跟踪过程中可以稳定输出目标的运动轨迹。

1 标准GLMB滤波算法

传统基于RFS的目标跟踪算法无法形成目标运动轨迹。为此,文献[9-10]提出GLMB滤波算法,并给出了具体实现方法。该算法综合运用MHT多帧平滑思想和标签RFS理论,可在低信噪比感知场景中保持跟踪精度并形成目标航迹。

某时刻目标状态标签随机集可以描述为

X={(x1,l1),(x2,l2),…,(xN,lN)}

(1)

式中,xi∈Xj为目标状态向量;Xj为j维目标状态空间;li∈L为目标对应标签;L为标签值空间;X为Xj×L形成的标签RFS空间;ξ(X)为X对应的标签值集合。

多伯努利随机集定义为

(2)

式中,ri为目标存活概率;pi(x)为对应目标概率分布函数。类比随机变量函数,定义集合指数函数为

(3)

式中,定义h(φ)=0。定义广义克罗内克函数和集合包含函数为

(5)

GLMB随机集是由状态空间和目标离散标签空间共同构成的标签随机集,其统计概率分布为

(6)

式中,Δ(X)为离散标签指示函数;s为索引指数;S为指示空间;pS(x,l)为概率分布;ωS则为对应权重,其满足

(7)

存活目标预测概率分布为

π(G|X)=Δ(G)Δ(X)γξ(X)(ξ(X))·[φ(G;x,l)]

(8)

式中

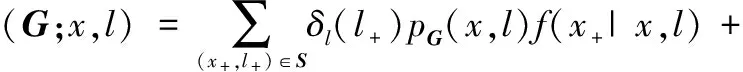
(1-γξ(X)(l))(1-pG(x,l))

(9)

式中,pG(x,l)为目标存活概率;f(x+|x,l)为单目标转移核函数。

将B设为新生目标标签RFS,b为对应的标签空间,则B的概率分布可描述为

πb(B)=Δ(B)ωb(ξ(B))[pb(·)]B

(10)

式中,pb(·)表示目标新生概率分布;ωb(ξ)表示新生目标权重。本文不考虑目标衍生过程,至此可得,下一时刻的目标状态X+=B∪S,新生目标与存活目标相互独立,其标签空间亦互不相交。综上可得GLMB预测方程为

π(X+|X)=πG(X+∩X|X)·πB(X+-X)

(11)

式中，X为当前目标形成的标签RFS空间,空间中元素(x,l)∈X；目标以量测率pD(x,l)形成量测,将目标量测D用多伯努利随机集可表示为

πD(D|X)={(pD(x,l),g(z|x));(x,l)∈X}

(12)

以K表示杂波量测RFS,假设杂波量测数目服从泊松分布,c(·)表示杂波空间分布,杂波量测概率分布可表示为

π(K)=e-λ[λc(·)]K

(13)

量测集Z由目标探测集D和杂波量测集K共同构成,量测似然函数可表示为

φZ(x,l;θ)]X

(14)

式中,θ为量测空间对状态空间的关联索引;Θ即为索引指示空间。

(15)

式中,当θ(l)>0代表关联具有唯一性;θ(l)=0代表量测为空。

2 星-凸随机超曲面扩展形态建模

现实跟踪场景中,运动体形态丰富、大小各异,传统外形建模方法难以有效刻画目标的轮廓细节。本文通过星-凸随即超曲面(random hypersurface model, RHM)对目标扩展形态进行精准建模。

图1 星-凸外形示意图Fig.1 Diagram of star-convex

为便于数学处理,将径向函数rk(φ)进行傅里叶级数展开,可描述为

(16)

目标量测由运动体表面量测源产生。采用星-凸RHM描述运动体量测源产生模型为

yk=mk+sk·rk(φ)·[cosφ,sinφ]T

(17)

式中,mk表示运动体质心状态;sk代表缩放因子,sk∈[0,1];[cosφ,sinφ]T代表在φ方向上的单位向量。量测zk由量测源yk生成,可描述为

zk=yk+vk

(18)

可得非线性量测方程为

zk=mk+sk·rk(φ)·[cosφ,sinφ]T+vk=h(xk,s)+vk

(19)

单量测似然函数闭合解可表示为

g(zk|xk)=∬δ[zk-(h(xk,s)+vk)]·

N(vk;0,Rk)·fs(s)dvkds=

(20)

式中,fs(s)表示缩放因子s的分布函数。以Nz,k表示量测数目,则多量测似然函数可表示为

(21)

3 ET-GLMB滤波算法

为实现ET-GLMB滤波算法,在某一时刻,将扩展目标状态建模为标签RFS

X={ξ1,ξ2,…,ξn}

(22)

式中,ξi表示带有标签的目标状态,以量测率pD(ξ,l)产生量测集合Wi,各集合形成目标量测集合D,其分布可表示为

(23)

假设杂波量测数目服从泊松分布,扩展目标量测似然函数可表示为

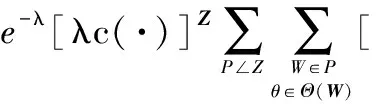
(24)

式中,p∠Z表示对量测集合Z的所有可能划分结果;W则表示某种划分中量测的非空子集;θ为建立在量测子集与目标之间的标签关联索引;Θ(W)即为标签索引指示空间。

(25)

假设k时刻统计概率分布满足式(6)所示GLMB随机集,下一时刻目标预测方程可表示为

(26)

式中

(27)

(28)

(29)

(1-γξ(ξ))pB(xk+1,l)

(30)

(31)

结合式(31)和式(24)推导可得,状态更新方程也是一个GLMB随机集,可表示为

(32)

其中

(33)

(34)

(35)

式中,φW(x,l;θ)已经在式(25)中给出；μλ和μx均为贝叶斯归一化常量。

4 仿真实验与分析

4.1 仿真实验场景1

为比较各滤波器在低信噪比观测场景下的性能差异,这里将所提算法ET-GLMB与扩展目标概率假设密度(extended target-PHD, ET-PHD)、扩展目标势概率假设密度(extended target-CPHD, ET-CPHD)滤波算法作性能对比分析,本实验部分参照文献[17]所设仿真环境。4个扩展目标依次出现,这里将目标检测概率设为pd=0.8,每一时刻杂波量测数目服从均值为λ=20的泊松分布,以较低的检测概率和较高的杂波量测数目构建低信噪比观测环境。目标运动初始状态和存在时间如表1所示。

表1 目标运动初始状态和存在时间

扩展目标质心线性运动模型为

(36)

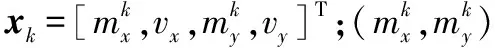
本文采用3种滤波算法对图2所示的星-凸超曲面目标进行跟踪。扩展目标外形状态由形状参数ek表示,本文采用11阶傅里叶级数展开式描述星-凸形扩展形态,每一时刻各目标产生的量测个数服从均值为λ=25的泊松分布,量测源在目标区域内均匀分布。目标量测由目标表面量测源产生,量测噪声[Rx,k,Ry,k]为零均值高斯白噪声,噪声标准差设为σRx=σRy=0.3 m。

图2 星-凸扩展目标和量测源分布Fig.2 Shape of star-convex extended target and measurements source distribution

图3给出在整个观测周期内扩展目标在X和Y坐标方向上的运动轨迹及量测值。图4～图6分别表示在单次蒙特卡罗实验中ET-PHD、ET-CPHD和本文所提的ET-GLMB滤波算法的状态估计结果。通过对比可从直观看出,在低信噪比观测场景中,本文所提的ET-GLMB滤波器的跟踪效果最好,而ET-PHD滤波器状态估计结果随着时间推移出现严重的估计偏差,这是由于ET-PHD仅用一阶矩描述并传递后验概率密度,具有优异的计算复杂度潜力,然而在低信噪比观测场景中,以一阶目标矩PHD强度替代目标概率分布将会损失大量信息,导致ET-PHD算法对目标漏检和杂波量测较为敏感。而本文所提ET-GLMB算法由于结合基于延迟逻辑的MHT理论,完整地迭代了MeMBer分布,对扩展目标能够持续稳定跟踪并输出航迹,跟踪效果优于ET-CPHD滤波算法。

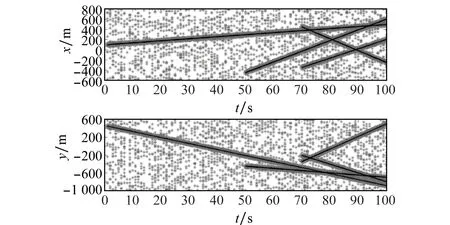
图3 扩展目标轨迹及量测图(I)Fig.3 Extended target tracks and measurements (I)

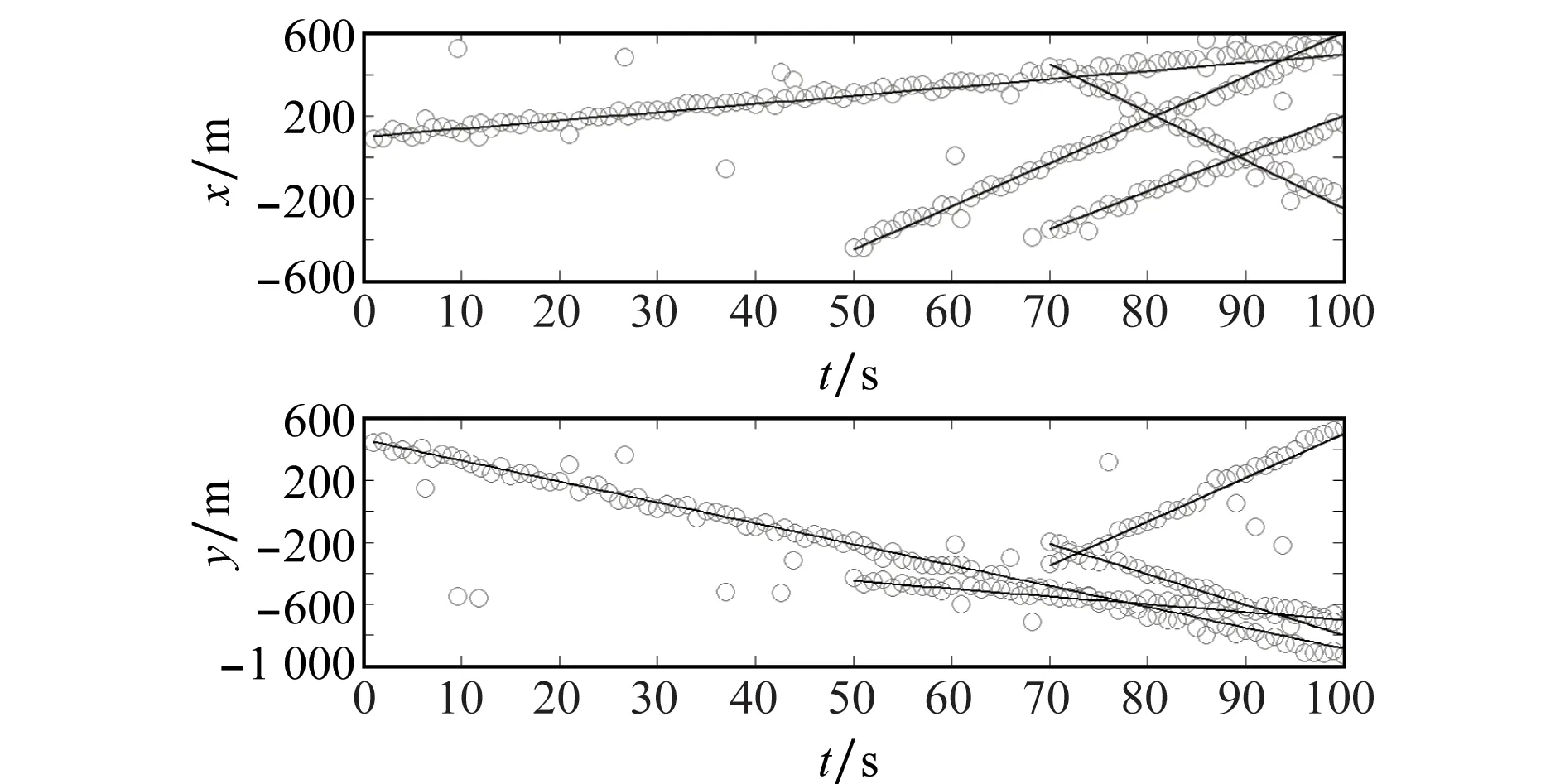
图4 ET-PHD滤波状态估计(I)Fig.4 Extended target state estimation based on PHD filter (I)

图5 ET-CPHD滤波状态估计(I)Fig.5 Extended target state estimation based on CPHD filter (I)

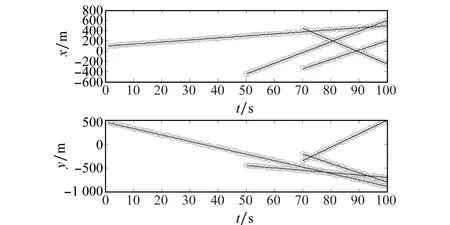
图6 ET-GLMB滤波状态估计(I)Fig.6 Extended target state estimation based on GLMB filter (I)

图7给出3种滤波算法对扩展目标数目估计结果对比。图7中浅灰色阴影表示ET-CPHD算法势估计统计实验标准差,深灰色阴影表示ET-GLMB滤波器势估计统计实验标准差。可以看出,低量测率条件下基于一阶矩近似的ET-PHD滤波算法的瞬时势估计极不稳定,在观测中存在势估计失真的问题。ET-GLMB和ET-CPHD滤波算法均可对扩展目标数目进行无偏估计,然而ET-CPHD算法势估计标准差明显大于本文所提算法,这是由于所提算法运用多帧量测平滑思想递推多伯努利参数,提高了势估计稳定性,验证了所提算法在低信噪比环境下的优异性能。

OSPA距离定义为

(37)

图7 扩展目标势估计图(I)Fig.7 Number estimation of the extended targets (I)

根据经验将设置参数p=2,c=80。图8表示3种滤波方法的状态估计OSPA脱靶距离。图8中深灰色和浅灰色区域分别表示ET-GLMB和ET-CPHD滤波算法的OSPA距离实验标准差。扩展目标2在第50时刻出现,在第70时刻,目标3、目标4同时出现。

图8 OSPA距离对比图(I)Fig.8 Comparison of OSPA distance (I)

从图8中可以看出,在扩展目标数目发生变化时,3种算法的状态估计性能均出现不同程度的下降。通过对比可以得出,在低信噪比观测场景中,ET-PHD的跟踪性能显著下降,这是由于算法假设量测数目需服从泊松分布,势估计误差的增大进而导致滤波器性能的严重下降。本文所提的ET-GLMB算法通过序贯蒙特卡罗方式实现算法时,无需采用聚类算法进行状态提取,因此能有效抑制杂波量测干扰,此外还结合了MHT思想,当漏检目标出现时利用N次回扫策略,使得粒子集得以保留,算法滤波精度更高,稳定性更好。

4.2 仿真实验场景2

为了更全面地反映所提算法的适用性和有效性,在紧邻目标跟踪环境下将所提算法ET-GLMB与ET-PHD和ET-CPHD滤波算法进行性能比较。观测区域共设置2个扩展目标,做同方向紧邻运动,其运动参数设置如表2所示,这里将目标检测概率设为pd=0.98,每一时刻杂波量测数目服从均值为λ=10的泊松分布,其他仿真环境同场景1相同。

表2 目标运动参数设置表

图9给出整个观测周期中扩展目标在x轴和y轴上的运动轨迹和真实量测图。

图9 扩展目标轨迹及量测图(Ⅱ)Fig.9 Extended target tracks and measurements (Ⅱ)

图10～图12分别表示在单次蒙特卡罗实验3种滤波算法的状态估计结果。不难看出,在紧邻目标跟踪场景下,ET-PHD滤波器的跟踪性能较差,滤波结果中依然存在数目较多的杂波估计,对目标的估计结果逐步偏离真实运动轨迹。所提算法ET-GLMB和ET-CPHD滤波算法均能取得较好的跟踪效果。

图10 ET-PHD滤波状态估计(Ⅱ)Fig.10 Extended target state estimation based on PHD filter (Ⅱ)

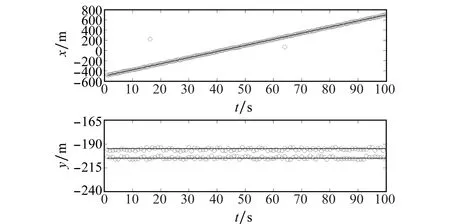
图11 ET-CPHD滤波状态估计(Ⅱ)Fig.11 Extended target state estimation based on CPHD filter (Ⅱ)

图12 ET-GLMB滤波状态估计(Ⅱ)Fig.12 Extended target state estimation based on GLMB filter (Ⅱ)

图13和图14分别给出3种算法的目标势估计对比图和OSPA统计距离对比图。根据仿真实验结果可以看出,在紧邻目标跟踪场景中,由于目标间的物理距离较近,导致ET-PHD和ET-CPHD滤波器出现不同程度的势低估现象,这也导致了OSPA统计距离误差的增大。所提算法ET-GLMB利用多帧信息进行状态平滑,有效克服了空间距离较近引起的势低估问题,另一方面,ET-GLMB算法在状态提取中无需进行不稳定的聚类过程,使得算法具有较好的稳定性。

图13 扩展目标势估计图(Ⅱ)Fig.13 Number estimation of the extended targets (Ⅱ)

图14 OSPA距离对比图(Ⅱ)Fig.14 Comparison of OSPA distance (Ⅱ)

5 结 论

本文针对低信噪比观测场景中多扩展目标跟踪精度下降和基于RFS理论的扩展目标跟踪算法不能输出目标航迹的问题提出了ET-GLMB算法,该算法利用星-凸RHM建模扩展目标外形信息,利用其与运动学状态之间的较强耦合关联,不仅可以输出目标的外形特征,还有效提高了跟踪精度。实验结果表明,在低信噪比探测场景和紧邻目标跟踪场景中,ET-GLMB算法可以有效输出目标运动轨迹,对多扩展目标数目和状态估计的跟踪精度和稳定性也优于ET-CPHD和ET-PHD滤波算法,滤波器整体性能得以大幅提升。

[1] 石章松, 刘忠. 目标跟踪与数据融合理论及方法[M]. 北京: 国防工业出版社, 2010: 143-167.

SHI Z S, LIU Z. Method and theory of target tracking and data fusion[M]. Beijing: National Defense Industry Press,2010:143-167.

[2] 陈金广. 目标跟踪系统中的滤波方法[M]. 西安: 西安电子科技大学出版社, 2013: 168-183.

CHEN J G. Method and theory of target tracking and data fusion[M]. Xi’an: Xi’an Electronic Science & Technology University Press, 2013: 168-183.

[3] DRUMMOND O E, BLACKMAN S, PETRISOR G C. Tracking cluster and extended objects with multiple sensors[C]∥Proc.of the SPIE International Conference on Signal and Data Processing of Small Targets, 1990: 362-371.

[4] 刘妹琴, 兰剑. 目标跟踪前沿理论与应用[M]. 北京: 科学出版社, 2015: 202-203.

LIU M Q, LAN J. Advance theory and application of target tracking[M]. Beijing: Science Press, 2015: 202-203.

[5] MATHERON G. Random sets and integral geometry[M]. New York: Wiley, 1975.

[6] MAHLER R. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Trans.on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.

[7] MAHLER R. PHD filters of higher order in target number[J]. IEEE Trans.on Aerospace and Electronic Systems, 2007, 43(4): 1523-1543.

[8] MAHLER R. Statistical multisource multitarget information fusion[M]. Boston: Artech House, 2007.

[9] VO B T, VO B N. Labeled random finite sets and multi-object conjugate priors[J]. IEEE Trans.on Signal Processing, 2013, 61(13): 3460-3475.

[10] VO B N, VO B T, PHUNG D. Labeled random finite sets and the Bayes multi-target tracking filter[J]. IEEE Trans.on Signal Processing, 2014, 612(24): 6554-6567.

[11] GILHILM K, GODSILL S, SALMOND D. Poisson models for extended target and group tracking[C]∥Proc.of the Data Processing of Small Targets, 2005: 230-241.

[12] KOCH J W. Bayesian approach to extended objects and cluster tracking using random matrices[J]. IEEE Trans.on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059.

[13] MICHAEL B, STEPHAN R, KARL G, et al. A generalised labelled multi-bernoulli filter for extended multi-target tracking[C]∥Proc.of the 18th International Conference on Information Fusion, 2015: 991-998.

[14] LAN J, LI X R. Tracking of maneuvering non-ellipsoidal extended object or target group using random matrix[J]. IEEE Trans.on Signal Processing, 2014, 62(9): 2450-2463.

[15] BAUM M, HANEBECK U D. Shape tracking of extended object and group targets with star-convex RHMs[C]∥Proc.of the 14th International Conference on Information Fusion, 2011: 338-345.

[16] RISTIC B, VO B N, CLARK D, et al. A metric for performance evaluation of multi-target tracking algorithms[J].IEEE Trans.on Signal Processing, 2011,59(7): 3452-3457.

[17] 曹倬,冯新喜,蒲磊,等.基于高斯混合概率假设密度滤波器的扩展目标跟踪算法[J].系统工程与电子技术,2017,39(3):494-499.

CAO Z, FENG X X, PU L, et al. Multiple extended targets tracking algorithm based on Gaussian-mixture probability hypothesis density filter[J]. Systems Engineering and Electronics, 2017, 39(3): 494-499.