城市环境车联网中基于近似算法的RSU部署方案

朱钧宇，黄传河，范茜莹，覃匡宇，付斌



城市环境车联网中基于近似算法的RSU部署方案

朱钧宇1，黄传河1，范茜莹1，覃匡宇1，付斌2

（1. 武汉大学计算机学院，湖北 武汉 430072；2. 美国得克萨斯里奥格兰德河谷大学，得克萨斯 爱丁堡 78539）

为了使用尽可能少的RSU实现对目标区域的有效覆盖，设计街道模型，将对区域的覆盖转化为对区域内街道的覆盖，然后，在该模型下提出基于贪心策略的多项式（GBP, greedy-based polynomial）时间近似算法，得到RSU的部署方案以解决覆盖问题。针对城市中一些地形复杂的区域，设计Cue模型（complex urban environment model），将目标区域划分为子区域，然后提出基于shifting策略的多项式时间近似算法，并对算法的近似比率和时间复杂度进行了理论分析与证明。仿真结果表明，算法GBP能够有效地解决城市环境车联网中的区域覆盖问题。

车联网；RSU部署；区域覆盖；近似算法

1 引言

车辆自组织网络（VANET, vehicular ad hoc network）作为现代智能交通系统（ITS, intelligent transportation system）的重要组成部分，主要通过无线通信技术来提高道路安全和交通运营效率，在辅助安全驾驶的同时提供多方面的娱乐服务信息，来提升驾驶员和乘客的交通体验[1]。VANET主要由车辆节点和路边节点（RSU, road side unit）组成，其主要通信方式分为2种：车辆与车辆（V2V, vehicle-to-vehicle）之间的通信以及车辆与RSU（V2R, vehicle-to-RSU）之间的通信，V2V使车辆可以与相邻车辆节点共享信息，V2R使RSU能够与其通信范围内的车辆节点进行信息交互[2]。

作为VANET的辅助通信设施，RSU可以应对VANET中因节点的快速移动引起的动态拓扑变化，能有效地解决VANET的接入问题以及改善车辆节点之间的通信质量[3]。另外，在VANET中部署RSU实现对道路区域的覆盖，有助于紧急交通信息在网络中的实时可靠传输[4]。然而，大量部署RSU不但会带来较高的安装和维护成本，还有以下难点：1) RSU的部署受车辆移动的影响，而车辆的实际运动轨迹是很难提前获取的；2) RSU的候选部署点集合很大，从中选取最优RSU部署点的过程比较复杂；3) RSU的部署受到很多因素的影响，如交通特征、可部署RSU的数量以及道路网络的拓扑结构和地理特征[5,6]。因此，在RSU数量受限的条件下，如何选择最优的位置来部署RSU，实现区域的覆盖以增强网络连通性，成为一个重要的问题。

本文主要研究了VANET中RSU的部署方案，实现目标区域的覆盖以保证其网络连通性，更好地为VANET中信息的实时可靠传输提供服务。为此，提出以下问题：假设城市环境中存在若干RSU候选点可供选择，如何进行RSU的部署，能够使用最少的RSU实现目标区域的覆盖。针对上述问题，本文首先提出了街道模型，该模型中RSU最多覆盖条街道并且仅覆盖每条街道的一部分。在此模型下，设计了采用基于贪心策略的多项式（GBP, greedy-based polynomial）时间近似算法来获取RSU的部署方案，通过将区域覆盖问题转化为区域内街道的覆盖问题，首先，得到覆盖每条街道的RSU集合，然后，求得所有街道的RSU集合，取并集就是覆盖目标区域所需的RSU集合。本文主要考虑RSU的部署问题，其中，假定RSU拥有足够的信号强度，同时具备足够的处理能力和带宽，能够满足服务质量和通信容量等需求。

另外，由于城市环境中某些地形比较复杂，街道信息难以获取，不宜采用街道模型来解决区域覆盖问题。因此，针对一些地形复杂的城市区域，本文设计了Cue模型，结合Hochbaum等[7]提出的shifting策略，提出了一种多项式时间近似算法。算法将目标区域划分为不同分区，然后，得到每个分区的RSU部署方案，选择使用RSU最少的方案，即近似最优RSU部署方案。通过理论分析可知，该算法能够取得较高的近似精度。

综上所述，本文的主要贡献包括以下3个方面。

1) 本文提出了街道模型，在该模型中，每个RSU至多覆盖条街道且仅覆盖每条街道上的一个区间。基于该模型，将区域覆盖问题转化为对区域内街道的覆盖问题，然后，设计了多项式时间近似因子为的近似算法GBP。

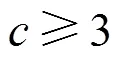
3) 针对城市环境中一些地形复杂的区域，由于街道信息难以收集，采用街道模型的效果不是很理想。本文提出了Cue模型，然后，设计了基于shifting策略的多项式时间近似算法，通过将目标区域划分为子区域，找出子区域的覆盖方案，进而得到目标区域的覆盖方案。最后，对算法进行了相应的理论分析与证明。

2 相关工作

通常用以下几个因素来衡量VANET中RSU部署方案的性能，如区域的覆盖率[8]、安装和维护设施的成本以及RSU辅助下信息传输的时延[9]。现有的工作主要研究如何平衡这些因素以实现理想的网络性能和通信质量[10]。

Omar等[11]提出了新的网关部署策略，在最小化网关安装成本的同时保证了车辆和网关通信的概率大于预先定义的阈值，同时最大化提出的目标函数值，所提算法假设道路上车辆的数目以及车辆在城市的每个地点相遇的概率为已知信息。然而，道路上车辆的数目以及车辆的相遇概率等信息不仅涉及用户的隐私，在实际情况下也是很难收集的。

Trullols等[12]针对DP（dissemination point）的部署问题，讨论了3种不同的区域覆盖问题形式，包括最大覆盖率问题（MCP, maximum coverage problem）、背包问题（KP, knapsack problem）以及与时间阈值相关的最大覆盖问题（MCTTP, maximum coverage with time threshold problem）。为了能够让DP在目标区域内覆盖更多的车辆，本文主要研究MCP，提出了简单的启发式算法，提高车辆和DP之间的通信性能，同时优化传输时延。该启发式算法能够在较大规模的环境下得到近似最优的方案，但是只有在获取车辆移动特征的前提下才能实现对移动用户的近似最优覆盖。

基于Trullols等[12]的研究，Cavalcante等[13]提出了一种基因算法（GA）用来解决MCTTP。Lin等[14]提出了一种车载骨干网络协议来动态支持从RSU到沿着高速公路行驶的车辆的信息流，然后提出了一种分析模型，以精确表征在规定的中断概率约束下可达到的最大吞吐率。根据OGM （overlap based greedy method），Rizk等[15]提出了在城市和乡村地区基于贪心算法的RSU部署方案，且主要考虑RSU的覆盖范围和重复覆盖率，实现了较好的目标区域覆盖效果。

为了最小化RSU的部署数目，Yan等[16]提出了在交叉路口安装AP（access point）的问题，分别讨论了如何使用最少的AP来保证区域内的车辆均在网络覆盖内以及在有限的预算下部署AP才能最大化网络可覆盖的车辆比例，然后，提出了多项式时间启发式算法（ABS, adapted-bipartite-based heuristics），通过使用ABS，证明了在普通平面图中的NP-hard问题均可在二分图中多项式时间内解决。Zhu等[17]研究基站可最大限度地延长城市覆盖范围的关键问题，然后，提出了最大化预期感测覆盖范围的新目标，同时考虑到了车辆的随机移动性和车辆行驶的规律。Cheng等[18]采用背包斯坦纳树（KCST, knapsack constrained Steiner tree）模型来描述特定区域的覆盖问题，然后，利用拉格朗日分解方法来求近似最优方案，同时考虑了安装预算和网络覆盖率。

Wang等[19]分析了VANET在RSU辅助下的信息传输时延，并提出了数学模型来描述道路信息传输的平均时延和邻居RSU之间距离的关系，该结果为时延要求较高的交通应用提供了一种可参考的RSU部署距离。Zhang等[20]设计了一种通用的系统架构来优化车联网的性能，分别针对实时交通和时延容忍交通2种情况进行分析，得到了2种不同情况下获得的吞吐量，并对时延容忍交通的时延界限作了说明，最后，提出了AP部署算法，在满足服务质量的同时部署最少的AP。

Kim等[21]将不同状态的RSU部署方案相结合，分别在固定地点部署RSU、利用公共交通和政府拥有的可完全控制的车辆，提出了新的RSU部署框架，在控制预算的同时实现时空覆盖的最大化。Liu等[22]分析了VANET高速公路情况下紧急信息广播的总时延，进而得到了RSU最优部署数目和道路距离的关系。Jalooli等[23]以最小传输时延为目标，提出了基于安全应用的RSU部署算法。Mukherjee等[24]首次考虑了事件传输时RSU的成本开销以及其容量。Li等[25]同时考虑了VANET中车辆的多样性，数据的不同种类、大小和时间敏感性以及RSU的有限容量，提出了上下文感知的优化问题，并设计了相应的解决方案。为了实现特定区域内信息传输的成本最小，Li等[26]设计了四叉树模型来表示区域的层次分解，然后选择最优的RSU将信息转发到目标区域。

Sun等[27]提出了一种高成本效益的RSU部署方案，以保证任何地方的OBU（on board unit）能够在一定的驾驶时间内与RSU进行通信，并且调整路由来更新短期证书的额外时间开销是很小的。奎晓燕等[28]根据真实的车辆行驶数据提出了综合考虑中心性和均匀性的RSU部署算法，以优化网络整体性能。刘明等[29]对随机部署方式下的覆盖问题进行了研究，并且提出了一个数学模型，只要已知监测范围和节点感知半径的比值，就可以计算出达到服务质量期望所需要的节点数量。黄晓等[30]针对在实际应用中，节点随机部署可能出现与基站不能正常通信的问题，提出了一种使用与基站连通的节点作为代理解决基站不可达节点的方案，并根据节点存储的路由信息给出了一种节点连通性的判定算法。谢永等[31]提出了一种面向高速公路场景的无间隙协助下载方法，充分利用车辆和AP的交互，进一步提高协助下载的稳定性。

大多数工作着重于研究通过优化RSU的部署来提高网络吞吐量、降低消息传输时延以及RSU的安装维护开销，而本文针对不同的城市环境，将对目标区域的覆盖分别转化为对区域内街道的覆盖以及子区域的覆盖，然后在已有的RSU候选放置点中找出对应的近似最优RSU部署方案，能够有效地实现对目标区域的网络覆盖，有助于网络内信息的实时可靠传输。

3 网络场景和覆盖问题描述

假定目标区域内所有街道均在一个平面图上，将交叉路口看作图中的节点。地理区域示意如图1所示，其中，虚线圆圈内的区域即所要覆盖的目标区域，RSU设施表示可供选择的RSU部署候选点。假定目标区域中有一系列随机分布的RSU部署候选点，本文的目标是从候选点中选择最少数目的位置点来部署RSU，从而实现区域的最大覆盖。

图1 地理区域示意

综上所述，本文将目标区域的覆盖问题转化为该区域内街道集合的覆盖问题，然后找出能够覆盖街道集合的最小RSU集合，实现区域覆盖的最大化。本文所用到的参数及其含义如表1所示。

表1 参数定义

4 基于贪心策略的街道区间覆盖方案

为了解决区域覆盖问题，将对区域内街道的覆盖问题转化为街道区间的覆盖问题。针对该问题，本节首先提出了街道区间覆盖算法，在此基础上提出了基于贪心策略的多项式时间近似算法，并对算法进行了相关的理论分析。

4.1 基于贪心策略的多项式时间近似算法

本节提出了街道模型，在该模型中，每个RSU至多覆盖条街道且仅覆盖每条街道上的一个区间。针对该覆盖模型，本文提出了基于贪心策略的多项式时间近似算法来解决目标区域的覆盖问题。

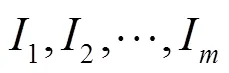
为了实现目标区域的有效覆盖，首先提出了区间覆盖算法（interval covering algorithm），如算法1所示。通过该算法得到覆盖目标区域内每条街道所需的RSU集合，在步骤6)中得到区间的最左覆盖I，将I加入目标集合，循环该过程直到区间被覆盖。在此基础上设计了基于贪心策略的多项式时间近似算法，如算法2所示，算法2在步骤5)调用算法1，得到区域内所有街道的覆盖方案，对所有街道的RSU集合取并集（步骤8)），即覆盖目标区域所需要的RSU集合。

算法1 区间覆盖算法

2) 令;

3) 令();

4) 令=I∪,∈{1, 2,…,};

5) 重复以下操作

6) if (∈I&最大)

7)=∪{I};

8)Uncovered= Uncovered − I;

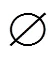
10) 输出为区间覆盖方案；

11) end

算法2 基于贪心策略的多项式时间近似算法

输入 路边单元RSU候选点集合，目标覆盖街道集合

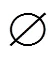
5) 调用区间覆盖算法（算法1）；

6) 返回街道S的覆盖方案C；

7) end for

9) end

4.2 路边节点对街道区间的覆盖

本节分析了一维街道区间覆盖问题的时间复杂度，并证明了街道模型下提出的多项式时间算法的近似因子。

引理1 对于一维区间覆盖问题，存在时间复杂度为(log)的算法，这里为算法输入的街道区间数目。

证毕。

定理1 在街道模型下，存在用于解决区域覆盖问题的近似因子为的多项式时间近似算法。

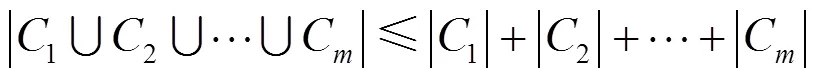
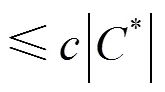
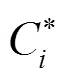
证毕。

4.3 NP-hard问题

本节将证明定理2，得到当每个RSU覆盖3条街道时，区域覆盖问题仍然是NP-hard问题。

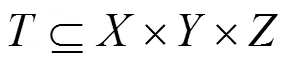
证毕。

5 基于shifting策略的区域覆盖方案

由于一些城市区域的地形比较复杂，难以获取具体街道信息，利用基于街道模型的GBP算法不能有效地解决区域覆盖问题。针对这种环境，本文设计了相应的Cue模型用于解决区域覆盖问题，该模型能够体现更多的城市环境特性。在该城市模型下，结合Hochbaum等[7]提出的shifting策略，本文提出了一个解决区域覆盖问题的多项式时间近似算法，并对算法进行了相应的理论分析和证明。

5.1 Cue模型及相关参数定义

基于shifting策略，本文设计了多项式时间近似算法用来解决区域覆盖问题，在该近似算法中，采用了Cue模型。与街道模型相比，该城市模型能体现更多的地理特征。模型中用到的术语及其含义如下。

定义1 City表示部署有路边节点RSU的城市环境。

1) City的街道图(,)为一个平面图，图中的节点表示交叉路口，边(,)为连接节点和的街道区间。

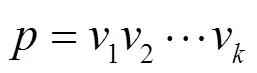
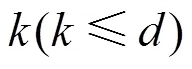
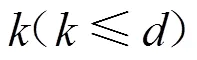
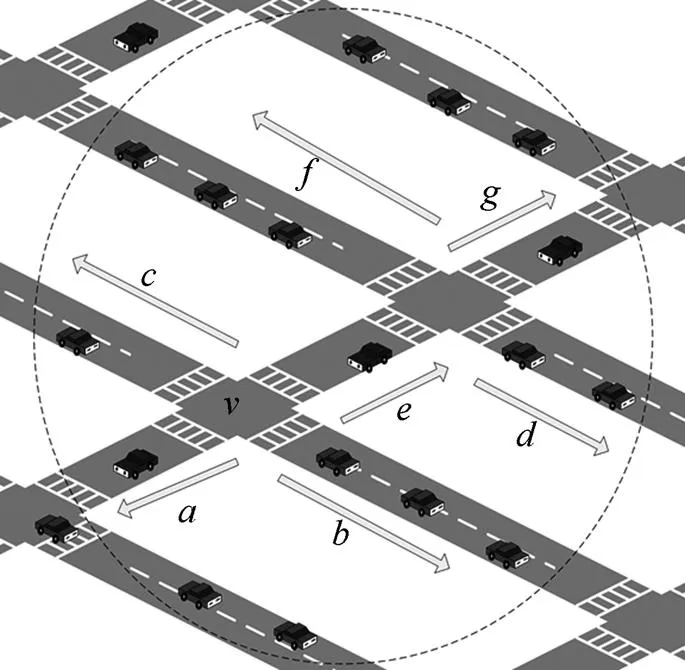
图2 d-star示例

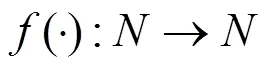
1) 每个RSU的传输范围为。

3) 每个RSU均具有的覆盖性质。

城市模型中的一个特例：当4时，每个RSU覆盖街道的一个区间，或交叉路口处的2条街道区间。

5.2 基于shifting策略的近似算法

本节首先介绍了近似算法采用的核心思想shifting策略，然后描述了所提出的多项式时间近似算法，并对算法的近似精度和时间复杂度进行了理论分析和证明。文献[7]将shifting策略描述为一种统一的方法，用来解决大量的几何覆盖和装箱问题，并且可能适用于超出这些范围的问题。通过重复使用shifting策略，选择一个最有利的解决方案，可以得到分治算法的误差界。

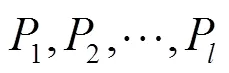
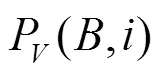
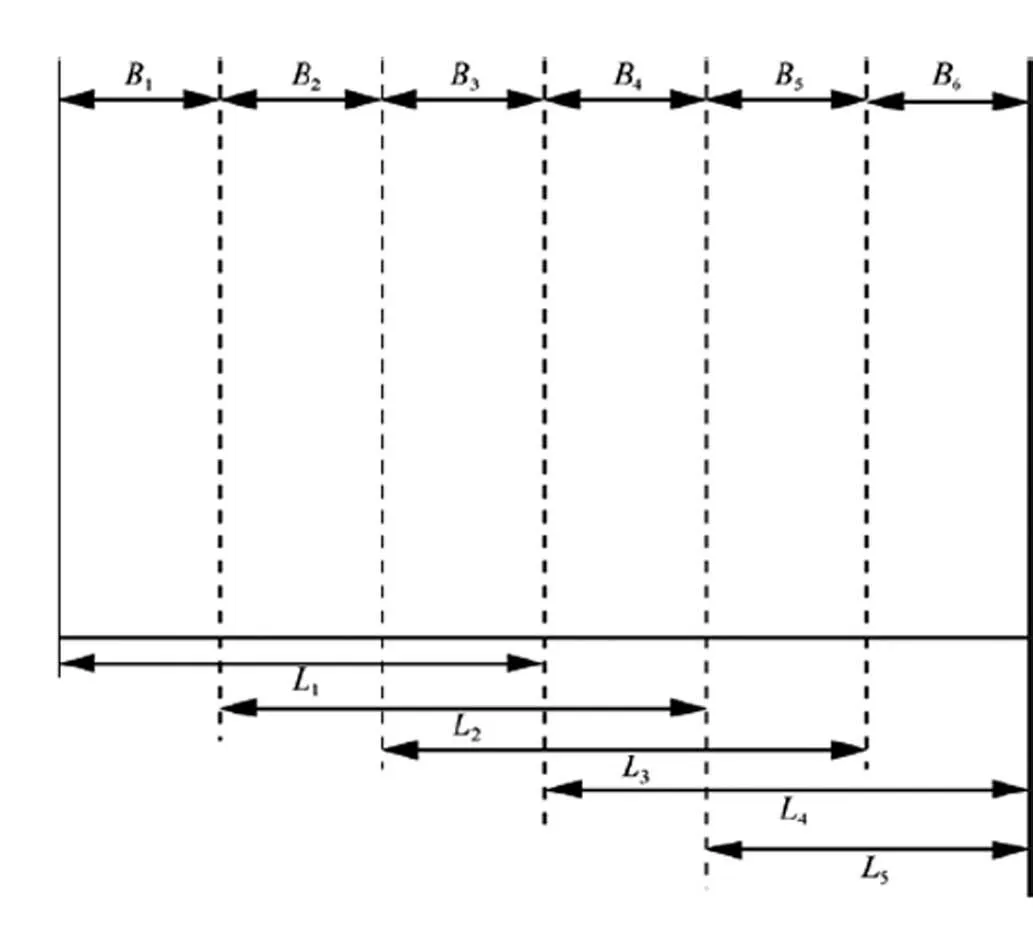
图3 shifting策略示例

算法3 基于shifting策略的多项式时间近似算法

输入 目标区域，街道区间集合，RSU集合，局部算法

输出 能够覆盖内街道区间的RSU集合()

5) for,,do

7) end for

8) for,do

10) end for

11) fordo

13) end for

15) end

引理3是正整数，对于最优覆盖方案C，假设目标区域内有交叉路口，则C中最多有个RSU覆盖。

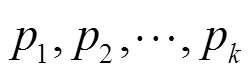
证毕。

证毕。

证毕。

本文的结果与标准的圆盘覆盖问题有些不同，在圆盘覆盖问题中，圆盘的位置并不是固定的。然而，在本文讨论的区域覆盖问题中，RSU的位置候选点均为随机生成后输入算法中的。

6 仿真结果与分析

在本节中，首先，介绍仿真环境；然后，描述了进行比较的算法以及用来评估算法的性能指标；最后，给出了仿真结果。

仿真考虑城市环境VANET中，有若干随机分布的RSU放置候选点可供选择。将本文提出的基于贪心策略的多项式时间近似算法GBP应用于实际的城市环境，与其他RSU部署方案进行比较，通过仿真来评估算法的性能。

6.1 仿真设置

综上所述，在该目标区域内存在若干个可供选择的RSU放置点，为了评估RSU候选点数目对算法性能的影响，在仿真中假设RSU候选点数目可以在一定范围内进行设置。RSU的通信范围为200 m，RSU的放置点通常为交叉路口或沿着道路放置。

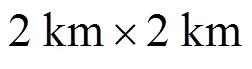
本节通过仿真对提出算法的有效性进行了验证和讨论，将所提出的基于贪心策略的多项式时间近似算法GBP与Yan等[16]提出的Tailor-方案以及Cheng等[18]提出的算法BCC（budgeted continuous coverage）进行比较，用来评估算法的性能。通过比较RSU候选点数目的变化对区域覆盖率（RSU部署方案所覆盖的区域与实际区域的比率）、计算时间以及近似比率（算法得到的RSU部署方案产生的区域覆盖与最优覆盖方案产生的区域覆盖的比率）等指标的影响，对算法性能进行评估。

6.2 仿真结果

本节将讨论当RSU候选点数目变化时，GBP、Tailor-以及BCC算法对应的区域覆盖率、计算时间以及近似比率的变化情况。

6.2.1 区域覆盖率

图4和图5分别显示了城市1和城市2共2种城市环境下由算法GBP、Tailor-和BCC产生的区域覆盖率。仿真结果反映了各算法的区域覆盖率与目标区域内可供选择的RSU候选点数目的关系。可以看出，在2种不同的城市环境下，GBP算法的区域覆盖率优于Tailor-方案和BCC算法各自产生的覆盖率。随着RSU的部署候选点增多，所有算法的覆盖效果均有所提高，这是因为当候选点位置增多时，算法选择用于区域覆盖的RSU数目也随之增加，从而覆盖更大的区域范围。另外，当城市环境下的道路拓扑结构变复杂时，可能会导致相对较低的区域覆盖率，特别是在该区域只有少数RSU的情况下。

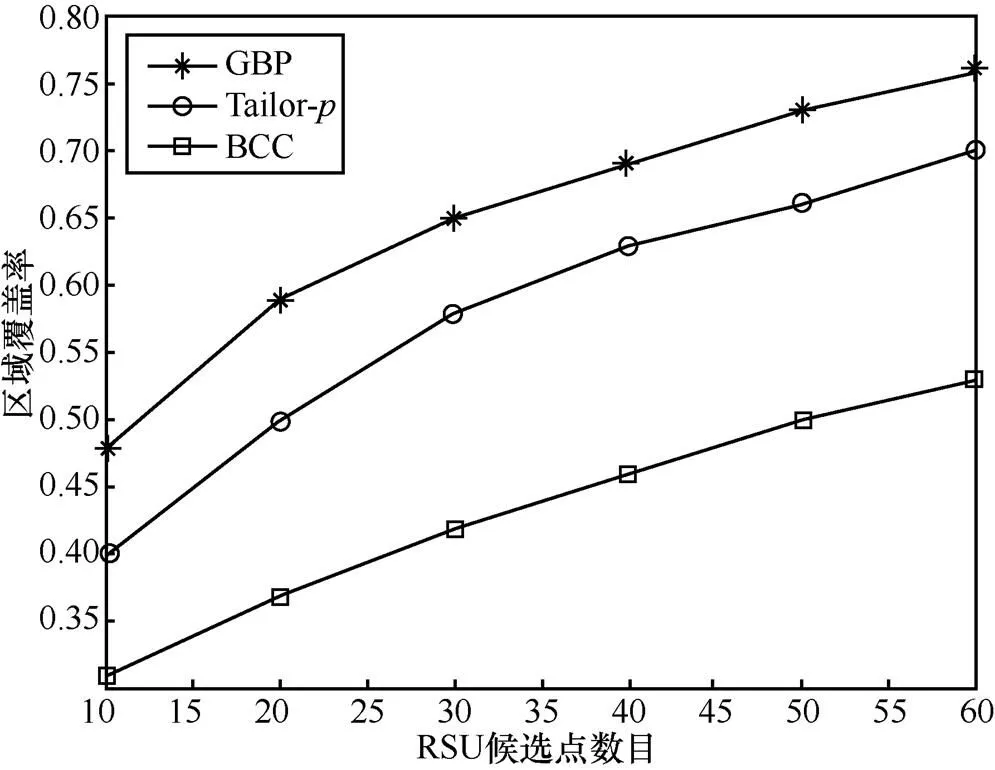
图4 覆盖率和RSU候选点的关系（城市1）

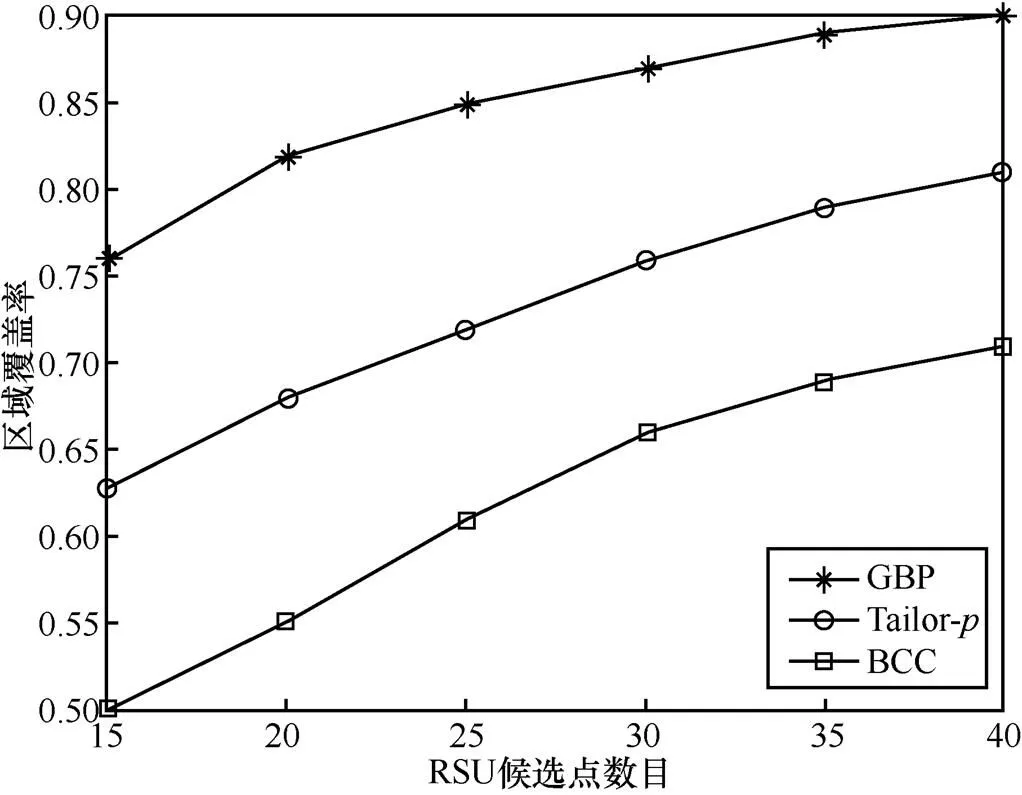
图5 覆盖率和RSU候选点的关系（城市2）

因此，图4中算法的覆盖率低于图5中相应算法的覆盖率。同样可以看出，在常规的城市环境下，少量的RSU在很大概率上足以覆盖大部分目标区域。因此，通过在重要位置部署相对较少的RSU，更容易对目标区域产生较大的覆盖。

由GBP、Tailor-和BCC这3种算法在2种不同城市环境中RSU的部署结果可知，当分别设定为60和40时，GBP得到的区域部署方案对区域的覆盖效果优于Tailor-和BCC，从而反映了GBP算法对不同街道布局良好的适应性和可扩展性。

6.2.2 计算时间

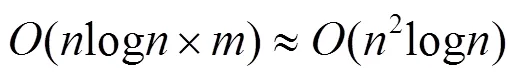
与Tailor-方案以及BCC算法相比，GBP主要根据区域街道的布局来求解RSU的部署方案，并不需要收集城市的交通信息和车辆的运动轨迹等信息，因此，GBP节省了计算交通信息以及车辆轨迹的时间。为了评估GBP、Tailor-以及BCC算法的计算复杂性，将城市1和城市2共2种环境下3种算法的计算时间分别表示为图6和图7。

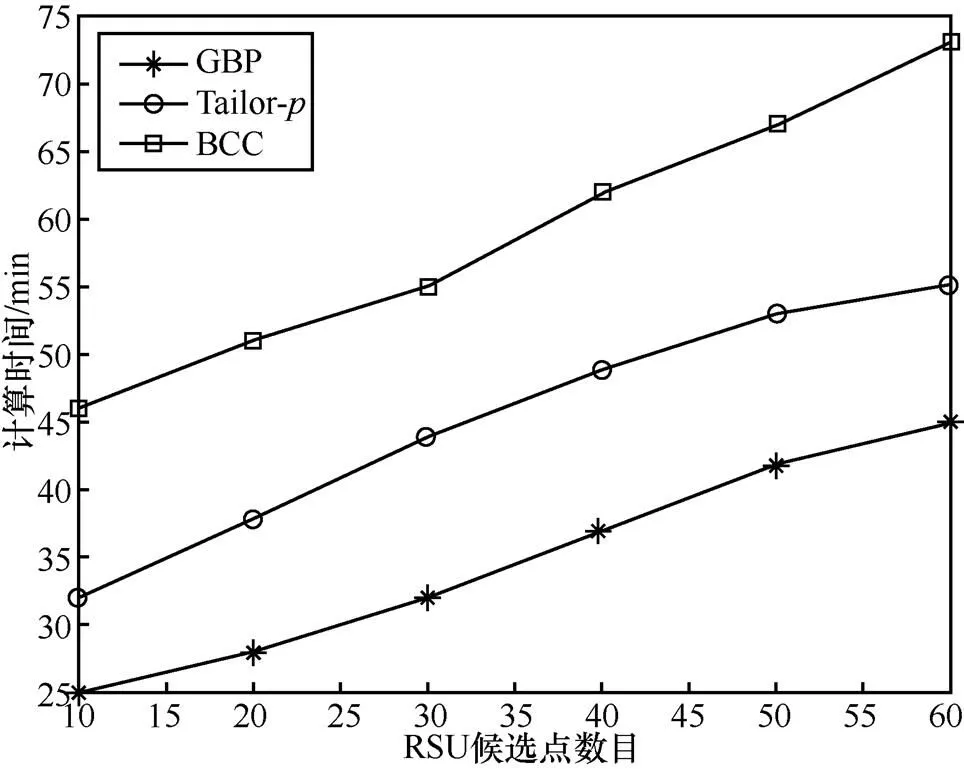
图6 计算时间和RSU候选点的关系（城市1）

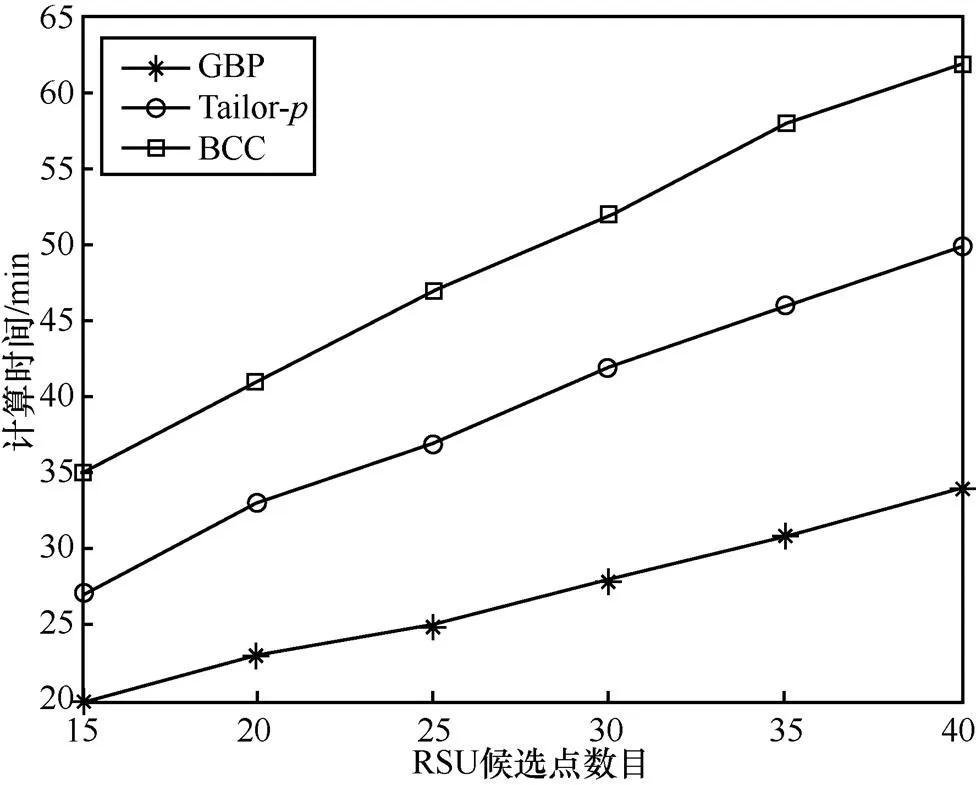
图7 计算时间和RSU候选点的关系（城市2）

仿真结果描述了各算法的计算时间与目标区域内可供选择的RSU数目的关系。当RSU候选点增加时，Tailor-和BCC计算时间增幅较大，而本文提出的GBP的计算时间增幅较小，并且Tailor-和BCC算法所消耗的时间均高于GBP算法。另外，比较图6和图7发现，由于城市1道路比城市2复杂，并且交叉路口较多，各算法在城市2中求解部署方案的计算时间明显比城市1有所降低。在GBP中，当候选点数量为15时，城市1得到部署方案的计算时间大约为27 min，在相同条件下，城市2的计算时间也不超过20 min，而BCC在2个城市区域的求解时间分别为47 min和35 min，Tailor-算法的花费时间则高于GBP同时低于BCC。当候选点数目分别增加到60和40时，BCC方案的计算时间差距随之变大，GBP和Tailor-的计算时间增幅较小。另外，如图6和图7所示，GBP计算时间变化不大，这是因为GBP计算时间主要与街道数目相关，同时也说明了GBP对不同的街道布局的适应性优于Tailor-和BCC算法。

6.2.3 近似比率

在2种城市环境下运行GBP、Tailor-和BCC这3种算法，得到各自的RSU部署方案。图8和图9分别描述了在城市1和城市2中RSU候选点数目变化的情况下得到部署方案的近似比率。由图8和图9可知，GBP和Tailor-算法的近似比率总是高于BCC算法，这是因为BCC算法产生的区域覆盖率较低，导致其近似比率较低。随着可供选择的RSU部署点数量增加，3种算法的近似比率均有所增长，而GBP算法得到的近似比率则明显高于Tailor-和BCC。值得注意的是，在图8和图9中，各算法得到的近似比率之间的差距越来越小，这是因为随着RSU部署数量的增加，系统开销也越来越大，因此，即使部署更多的RSU，算法带来的边际收益也不会得到显著提升，这从一定程度上说明了选择少量RSU进行合理的部署也会获得良好的网络性能。

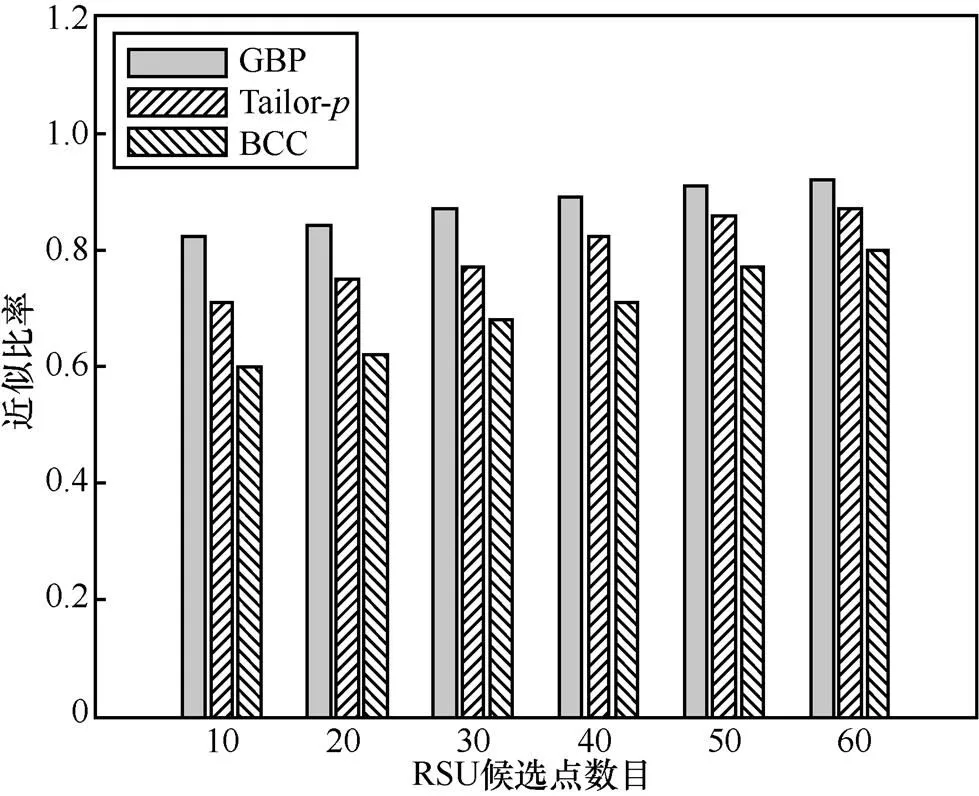
图8 近似比率和RSU候选点的关系（城市1）

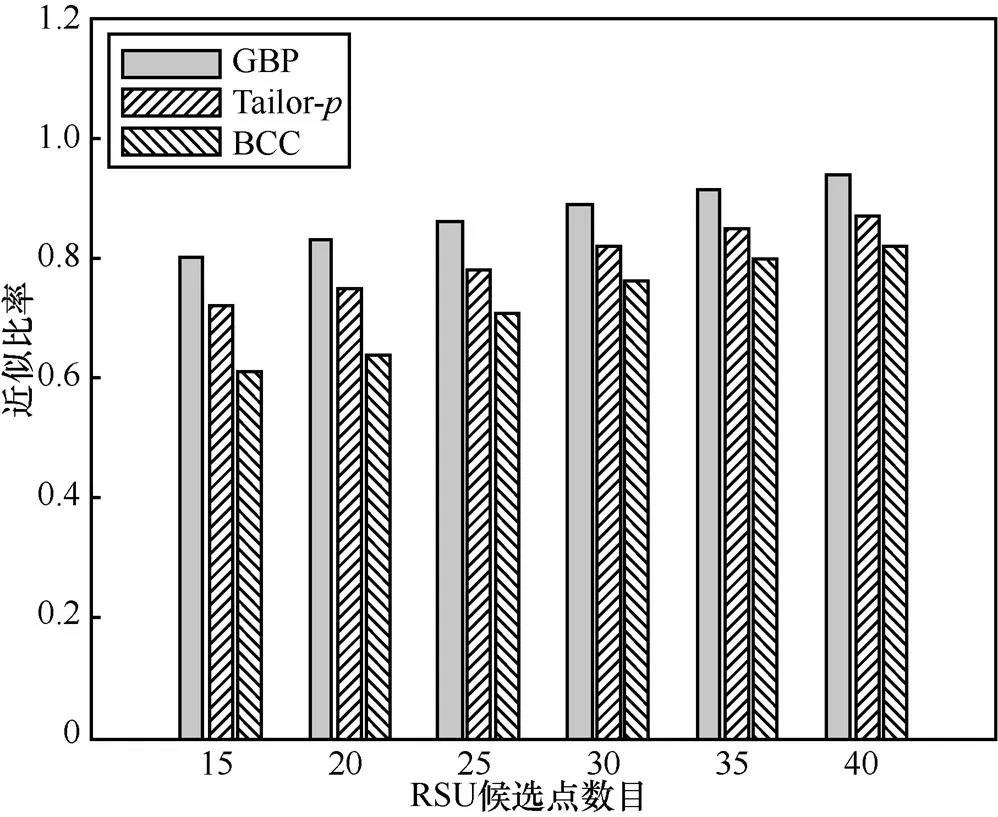
图9 近似比率和RSU候选点的关系（城市2）

7 结束语

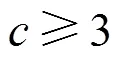
针对城市中地形比较复杂的区域，由于街道信息难以收集导致在该类环境下GBP算法不能有效地解决区域覆盖问题。针对该问题，结合VANET城市环境的特性，设计了能够表现更多地理特征的Cue模型，然后，提出了基于shifting策略的多项式时间近似算法，并对算法进行理论分析得到了算法的近似比率。最后，仿真实现了本文提出的采用贪心策略的多项式时间算法GBP，与其他相关算法进行比较并提供了仿真结果。仿真结果表明了该算法的有效性，能够在RSU候选点中合理部署RSU，给区域提供最大覆盖，同时降低了RSU部署的开销。

基于shifting策略的多项式时间近似算法中，使用了局部算法来求解分区的部署方案，未来拟研究比枚举法更好的局部最优算法或可求局部解的启发式近似算法，结合shifting策略以产生更有效的全局近似算法。

[1] 常促宇, 向勇, 史美林. 车载自组网的现状与发展[J]. 通信学报, 2007, 28(11): 116-126.

CHANG C Y, XIANG Y, SHI M L. Development and status of vehicular ad hoc networks[J]. Journal on Communications, 2007, 28(11): 116-126.

[2] 李丽君, 刘鸿飞, 杨祖元, 等. 车用自组网信息广播[J]. 软件学报, 2010, 21(7): 1620-1634.

LI L J, LIU H F, YANG Z Y, et al. Broadcasting methods in vehicular ad hoc networks[J]. Journal of Software, 2010, 21(7): 1620-1634.

[3] ENGLUND C, CHEN L, VINEL A, et al. Future applications of VANETs[M]// Vehicular Ad Hoc Networks. Switzerland: Springer, 2015: 524-544.

[4] XING M, HE J, CAI L. Utility maximization for multimedia data dissemination in large-scale VANETs[J]. IEEE Transactions on Mobile Computing, 2017, 16(4): 1188-1198.

[5] 陈立家, 江昊, 吴静, 等. 车用自组织网络传输控制研究[J]. 软件学报, 2007, 18(6): 1477-1490.

CHEN L J, JIANG H, WU J, et al. Research on transmission control on vehicle ad-hoc network[J]. Journal of Software, 2007, 18(6): 1477-1490.

[6] 姜海涛, 张宏, 李千目. 车载时延容忍网络路由协议研究[J]. 通信学报, 2013, 34(3): 76-84.

JIANG H T, ZHANG H, LI Q M. Research on routing protocol of vehicular delay-tolerant networks[J]. Journal on Communications, 2013, 34(3): 76-84.

[7] HOCHBAUM D S, MAASS W. Approximation schemes for covering and packing problems in image processing and VLSI[J]. Journal of ACM, 1985, 32(1): 130-136.

[8] LUO Z, GAN X, WANG X, et al. Optimal throughput-delay trade-off in manets with supportive infrastructure using random linear coding[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7543-7558.

[9] LU N, ZHANG N, CHENG N, et al. Vehicles meet infrastructure: towards capacity-cost tradeoffs for vehicular access networks[J]. IEEE Transaction on Intelligent Transportation System, 2013, 14(3): 1266-1277.

[10] HAJLAOUI R, GUYENNET H, MOULAHI T. A survey on heuristic-based routing methods in vehicular ad hoc network: technical challenges and future trends[J]. IEEE Sensors Journal, 2016, 16(17): 6782-6792.

[11] OMAR H, ZHUANG W, LI L. Gateway placement and packet routing for multihop in-vehicle Internet access[J]. IEEE Transactions on Emerging Topics in Computing, 2015, 3(3): 335-351.

[12] TRULLOLS O, FIORE M, CASETTI C, et al. Planning roadside infrastructure for information dissemination in intelligent transportation systems[J]. Computer Communications, 2010, 33(4): 432-442.

[13] CAVALCANTE E, AQUINO A, PAPPA G, et al. Roadside unit deployment for information dissemination in a VANET: an evolutionary approach[C]//The 14th Annual Conference Companion on Genetic and Evolutionary Computation. 2012: 27-34.

[14] LIN Y Y, RUBIN I. Throughput maximization under guaranteed dissemination coverage for VANET systems[C]//Information Theory and Applications Workshop. 2015:313-318.

[15] RIZK R, DAHER R, MAKKAWI A. RSUs placement using overlap based greedy method for urban and rural roads[C]//International Workshop on Communication Technologies for Vehicles. 2015: 12-18.

[16] YAN T, ZHANG W S, WANG G L, et al. Access points planning in urban area for data dissemination to drivers[J]. IEEE Transactions on Vehicular Technology, 2014, 63(1): 390-402.

[17] ZHU Y M, BAO Y C, LI B. On maximizing delay-constrained coverage of urban vehicular networks [J]. IEEE Journal on Selected Areas in Communications, 2012, 30 (4): 804-817.

[18] CHENG H, FEI X, ALMULLA M, et al. A knapsack constrained steiner tree model for continuous coverage over urban VANETs[C]//IEEE International Conference on Communications. 2014: 130-135.

[19] WANG Y, ZHENG J, MITTON N. Delivery delay analysis for roadside unit deployment in vehicular ad hoc networks with intermittent connectivity[J]. IEEE Transactions on Vehicular Technology, 2016, 65(10): 8591-8602.

[20] ZHANG B, JIA X, YANG K, et al. Design of analytical model and algorithm for optimal roadside AP placement in VANETs[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7708-7718.

[21] KIM D, VELASCO Y, WANG W, et al. A new comprehensive RSU installation strategy for cost-efficient VANET deployment[J]. IEEE Transactions on Vehicular Technology, 2017, 66(5): 4200-4211.

[22] LIU C, HUANG H, DU H. Optimal RSUs deployment with delay bound along highways in VANET[J]. Journal of Combinatorial Optimization, 2017, 33(4): 1168-1182.

[23] JALOOLI A, SONG M, XU X. Delay efficient disconnected RSU placement algorithm for VANET safety applications[C]//IEEE Wireless Communications and Networking Conference. 2017: 1558-2612.

[24] MUKHERJEE J C, GUPTA A, SREENIVAS R C. Event notification in VANET with capacitated roadside units[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(7): 1867-1879.

[25] LI Y, JIN D, HUI P. Contact-aware data replication in roadside unit aided vehicular delay tolerant networks[J]. IEEE Transactions on Mobile Computing, 2016, 15(2): 306-321.

[26] LI P, ZHANG T, HUANG C, et al. RSU-assisted Geocast in vehicular ad hoc networks[J]. IEEE Wireless Communications, 2017, 24(1): 53-59.

[27] SUN Y P, LIN X D, LU R X, et al. Roadside units deployment for efficient short-time certificate updating in VANETs[C]//IEEE International Conference on Communications (ICC). 2010: 1-5.

[28] 奎晓燕, 杜华坤, 肖雪峰, 等. 基于真实车载移动数据的RSU部署算法[J]. 北京邮电大学学报, 2015, 38(1): 114-118.

KUI X Y, DU H K, XIAO X F, et al. Realistic vehicular mobility trace driven RSU deployment scheme[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(1): 114-118.

[29] 刘明, 曹建农, 郑源, 等. 无线传感器网络多重覆盖问题分析[J]. 软件学报, 2007, 18(1): 127-136.

LIU M, CAO J N, ZHENG Y, et al. Analysis for multi-coverage problem in wireless sensor networks[J]. Journal of Software, 2007, 18(1): 127-136.

[30] 黄晓, 程宏兵, 杨庚. 无线传感器网络覆盖连通性研究[J]. 通信学报, 2009, 30(2): 129-135.

HUANG X, CHENG H B, YANG G. Research of connectivity for wireless sensor networks[J]. Journal on Communications, 2009, 30(2): 129-135.

[31] 谢永, 吴黎兵, 何炎祥, 等. 无间隙的车联网协助下载方法[J]. 通信学报, 2016, 37(1):180-190.

XIE Y, WU L B, HE Y X, et al. Non-intermittent cooperative downloading approach for VANET[J]. Journal on Communications, 2016, 37(1): 180-190.

[32] KARP R M. Reducibility among combinatorial problems[M]// New York: Springer, 1972: 85-103.

[33] HAKLAY M, WEBER P. OpenStreetMap: user-generated street maps[J]. IEEE Pervasive Computing, 2008, 7(4): 12-18.

[34] KRAJZEWICZ D. Traffic simulation with SUMO-simulation of urban mobility[M]//New York: Springer, 2010: 269-293.

RSU deployment planning based on approximation algorithm in urban VANET

ZHU Junyu1, HUANG Chuanhe1, FAN Xiying1, QIN Kuangyu1, FU Bin2

1. Computer School, Wuhan University, Wuhan 430072, China 2. The University of Texas Rio Grande Valley, Edinburg 78539, USA

To minimize the number of RSU deployed to cover a specific area, astreet model transforming the area covering problem to streets covering problem was designed, and a greedy-based polynomial (GBP) time approximation algorithm was developed to obtain the optimal RSU deployment for area coverage. For complex urban environments, a Cuemodel (complex urban environments model) was proposed. In this model, the target area was divided into different partitions. Then, based on shifting strategy, a polynomial time approximation scheme was designed. Theoretical analysis that include the approximation ratio and time complexity of the proposed algorithm were also presented. Simulation results show that GBP can efficiently solve the coverage problem in urban VANET.

VANET, RSU deployment, covering problem, approximation algorithm

TP393

A

10.11959/j.issn.1000-436x.2018008

朱钧宇（1987-），男，河南周口人，武汉大学博士生，主要研究方向为物联网、无线网络、车载自组织网络等。

黄传河（1963-），男，湖北随州人，武汉大学教授、博士生导师，主要研究方向为计算机网络（移动互联网、移动ad hoc网络、无线传感器网络、未来互联网）、物联网、网络安全、高性能计算等。

范茜莹（1990-），女，河南驻马店人，武汉大学博士生，主要研究方向为无线网络、算法设计与分析、车载自组织网络等。

覃匡宇（1974-），男，壮族，广西马山人，武汉大学博士生，主要研究方向为软件定义网络（SDN）、网络管理。

付斌（1964-），男，美国得克萨斯州人，美国得克萨斯里奥格兰德河谷大学终身教授，主要研究方向为算法设计与分析、生物信息、计算复杂性理论、无线网络等。

2017-08-11；

2017-12-25

黄传河，huangch@whu.edu.cn

国家自然科学基金资助项目（No.61772385, No.61373040, No.61572370）；美国国家科学基金会基金资助项目（No.0845376）

: The National Natural Science Foundation of China (No.61772385, No.61373040, No.61572370), The National Science Foundation Early Career Award of USA (No.0845376)