MapReduce框架下支持差分隐私保护的随机梯度下降算法

2018-03-14俞艺涵付钰吴晓平

通信学报 2018年1期

关键词：分布式计算可用性差分

俞艺涵，付钰，吴晓平

俞艺涵，付钰，吴晓平

（海军工程大学信息安全系，湖北武汉 430033）

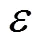
机器学习；随机梯度下降；MapReduce；差分隐私保护；拉普拉斯机制

1 引言

机器学习（ML, machine learning）作为人工智能的核心，可以利用现有数据，通过归纳、综合等方法使计算机实现具备自我学习与自我更新的功能。梯度下降算法是一种典型的求解无约束优化问题的方法，主要思想是朝着负梯度方向寻求目标的最优解。由于该算法具有适用性强、优化效果好等优点，其在机器学习中得到了普遍应用。随机梯度下降（SGD, stochastic gradient descent）算法作为梯度下降算法的一种，由于其在每次迭代过程中不需要遍历所有数据，更适合运用在大数据背景下的机器学习中，但其仍存在以下2个方面的问题。1) 随着大数据时代的数据量越来越大，需用分布式计算架构来满足随机梯度下降算法的计算需求。而在分布式计算架构下，随机梯度下降算法在每个计算节点所用样本的不全面性、节点间数据通信频繁造成开销过大等问题，都会导致算法的收敛速度下降[1]。如何在分布式计算框架下进行快速随机梯度下降算法的实现是亟待解决的关键性问题。2) 随机梯度下降算法在帮助人们运用机器学习、数据挖掘等技术不断探索、利用数据中有价值的信息，并以此作为评估、预测和决策等行为依据的同时，也存在着泄露数据集中敏感数据的风险，威胁数据隐私安全[2]。如何在利用大数据的同时，保证大数据中的敏感数据安全是近年来的研究热点。

针对问题1)，国内外学者做出了许多卓有成效的工作。文献[3]运用抽样概率的思想，使用特殊非均匀采样策略构建minibatch来减少随机梯度差异，但其本质需要依赖样本之间的直接关联性；文献[4]通过记录历史梯度，并在当前迭代中使用自适应平均的历史梯度来减少迭代中随机梯度的方差。然而，频繁的记录历史梯度将给存在众多参数的机器学习带来额外的负担。文献[5]提出采用残差最小化框架，修正随机梯度方向，提高随机梯度的稳定性，同时采用半随机梯度思想并提出一种分层半随机梯度下降新方法，来提高收敛速度。由于随机梯度下降算法不可避免地将出现多次更新迭代，这使MapReduce等分布式计算架构在处理随机梯度下降算法时，会出现因节点间的反复数据传递而造成的通信开销过大的问题。文献[6]提出在每一个分布式计算节点上完整地执行一遍梯度下降算法，通过平均模型合并得到最终模型。该方法减少了计算过程中的通信开销，但每一个节点的数据存在局限性，没有利用全局数据来提高运算性能。同时，在模型合并时，简单平均合并没有考虑到模型之间存在的差异性，可能会降低算法的收敛速度和最终模型的可用性。文献[7]利用文献[8]中提出的蝴蝶状通信机制，在每一轮迭代中，每个节点将迭代模型仅发送给另一个节点，并接受一个模型对本地模型进行更新。这样可使每一个节点能够充分利用全局数据来提高算法收敛速度与性能。同时，文献[7]还对模型的合并方法进行了优化，将各个更新模型的性能作为模型合并的加权依据，由此提高了算法性能。针对问题2)，部分学者将差分隐私（DP, differential privacy）保护引入随机梯度下降算法中，以此来应对大数据环境下的隐私泄露问题。文献[9]和文献[10]所提方法为目前较为先进的将差分隐私保护运用到随机梯度下降算法中的方法。文献[9]在随机梯度下降算法的每次迭代中加入扰动噪声，以此达到差分隐私保护的要求；文献[10]通过子集采样的方法来减少每次迭代的噪声量，同时可以保证最佳收敛。但是，以上2种方法都存在私密性与效率性以及可用性之间的矛盾，即保证私密性时，算法的性能以及最终模型的可用性将下降；相反，保证效率性与可用性时，扰动噪声的添加可能难以保证差分隐私保护的要求。

基于此，本文提出了一种在分布式计算环境下将差分隐私保护技术应用到随机梯度下降算法中，同时缓解数据私密性与算法效率性矛盾的新算法。该算法通过合理的数据分配方法和模型合并策略来提高随机梯度下降算法的收敛速度与性能，并以策略性的差分隐私保护预算分配进行随机噪声添加，使随机梯度下降算法的输出结果满足差分隐私。

2 差分隐私保护

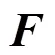
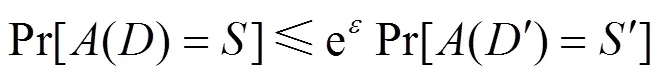
差分隐私保护通常对数据进行随机噪声添加和随机响应来达到隐私保护目的，主要的实现机制分别为拉普拉斯机制与指数机制。其中，拉普拉斯机制[12]适用于数值型保护，是随机梯度下降算法中最常用的差分隐私保护机制。查询函数的全局敏感度是决定满足差分隐私保护的随机噪声大小的关键因素。全局敏感度定义如下。

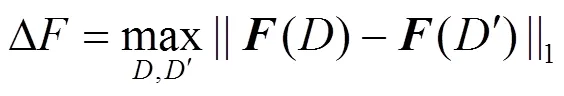
此外，差分隐私保护存在以下2个方面的组合性质[13]，是将差分隐私保护运用到反复迭代过程中，证明算法满足差分隐私保护以及合理分配差分隐私预算的基础。

3 MapReduce框架下的DP-SGD算法

本文所提算法的功能是在MapReduce分布式计算框架下，实现对随机梯度下降算法提供有效的差分隐私保护，并保证算法具有较高的效率性。即保证当数据集中改变任何一个记录时，随机梯度下降算法所得到目标模型的变化不会泄露数据集的隐私信息。也就是说，拥有丰富背景知识的攻击者无法通过手头上与目标数据集高度相似（极端情况下只相差一条记录）的数据集，通过目标模型的建立得到数据集中单个数据的隐私信息。

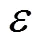
现有的差分隐私保护随机梯度下降算法[9,10]存在的最主要问题是算法效率性较低，其主要原因是随机梯度下降算法需要通过反复迭代来使目标模型收敛，而算法的反复迭代将造成在MapReduce等分布式计算框架计算过程中，产生大量节点之间的通信开销；而在每轮迭代中，添加随机噪声也不利于目标模型的收敛。因此，本文对MapReduce框架下的DP-SGD算法进行设计，采取了改进的数据分发与模型合并方案以及随机噪声的添加方法。算法主要符号说明如表1所示。

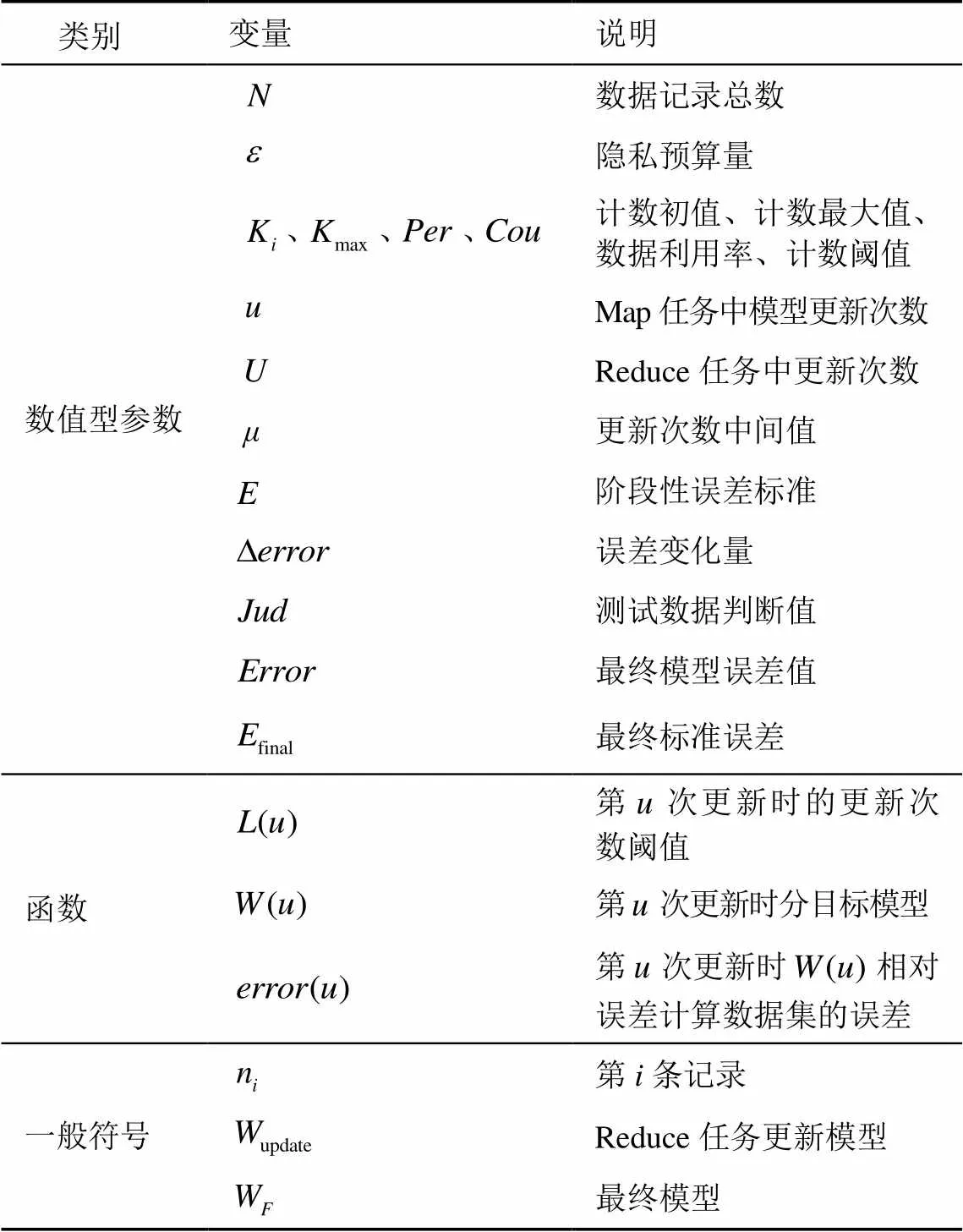
表1 DP-SGD算法设计符号说明

3.1 算法设计

3.2 隐私预算及隐私性分析

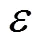
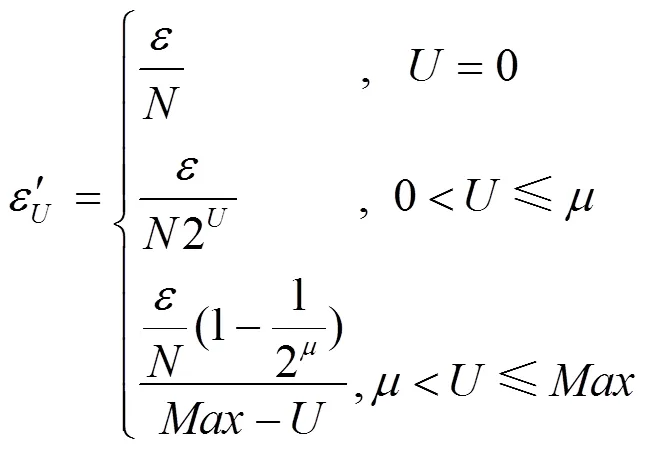
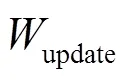
3.3 效率性及可靠性分析

本文所提MapReduce框架下的DP-SGD算法通过关键参数的设置，对隐私预算、计算资源进行合理规划，并优化了数据分配以及模型合并的方法。

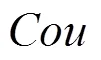
2) 阈值函数()

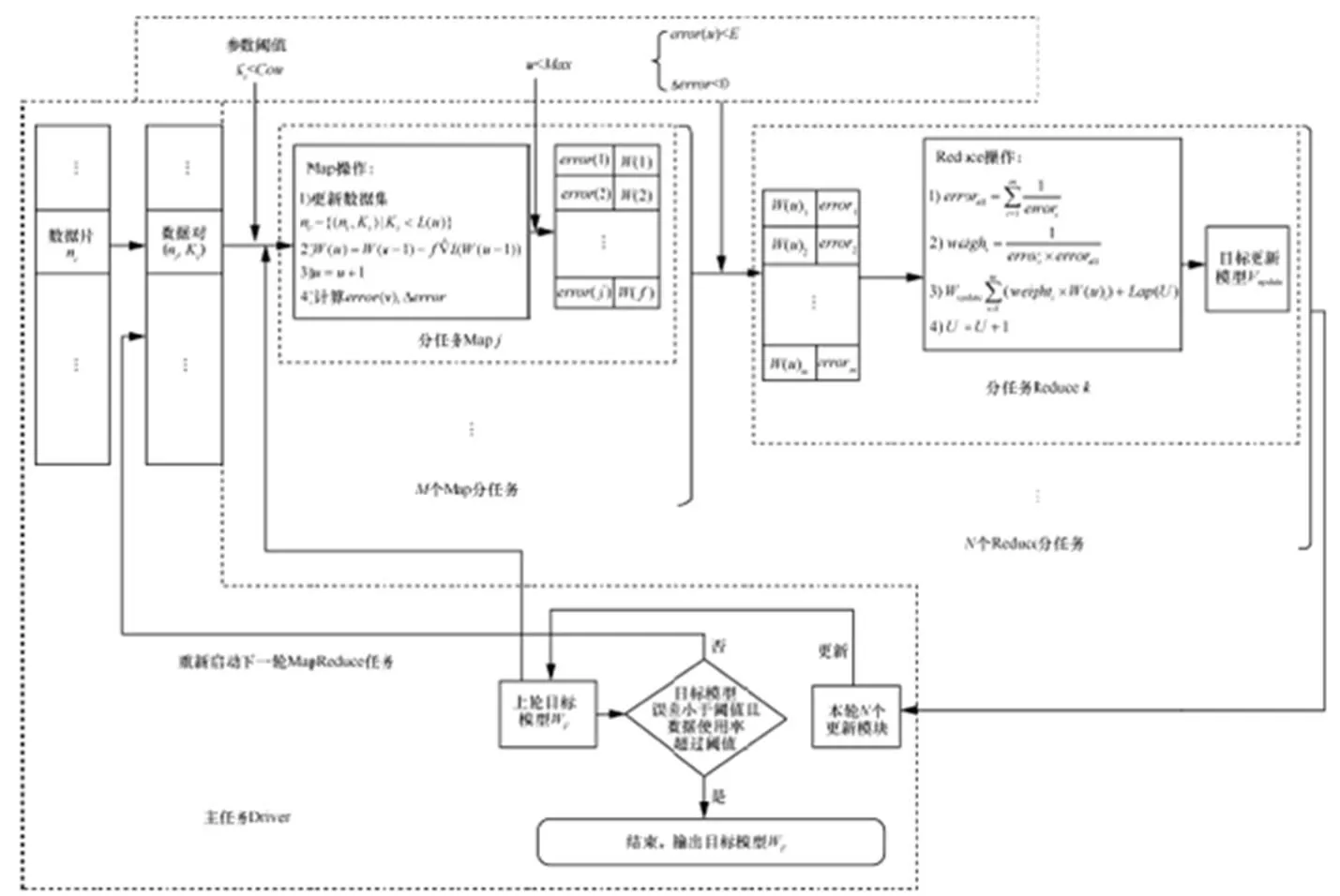
图1 MapReduce 框架下的 DP-SGD 算法流程

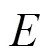
5) 算法终止参数、final、max、

4 算法效率及可用性实验

本文所提算法主要是对MapReduce计算环境下的随机梯度下降算法进行优化，并提供差分隐私保护。算法的隐私性已得到证明，为此，在实验中主要对算法的效率性与可用性进行实验。

实验中的分布式计算平台由5台IBM X系列机架式服务器组成，每台服务器配置如下：3.30 GHz CPU，2.99 GB内存，Ubuntu12.04操作系统，并部署Hadoop0.20.2。算法由Java软件进行开发。

实验选择MNIST手写图像数据集作为实验数据集。MNIST是由Google实验室和纽约大学柯朗研究所建立的手写数字数据库，包含60 000张训练图像和10 000张测试图像。实验分别采用文献[9]中的SCS13算法、文献[10]中的BST14算法以及本文所提算法建立相同逻辑回归模型，对MNIST数据集进行手写数字分类实验。

4.1 算法运行效率实验

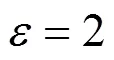
算法运行时间如图2所示，可以发现A算法由于随机噪声的添加，运行时间较B算法有明显增加，且随着数据量的增大，运行时间的增量也随之增加。这是由于数据量的增加要求目标模型需要更多的迭代更新次数才能达到算法完成的标准，而每次模型迭代更新时却需要加入阻碍模型收敛的随机噪声引起的。同时，每轮迭代中，都会有一部分Map节点与Reduce节点之间、Reduce节点与主节点之间以及子节点与主节点之间的数据传递所造成的额外通信开销，这也导致了算法运行时间的增加。

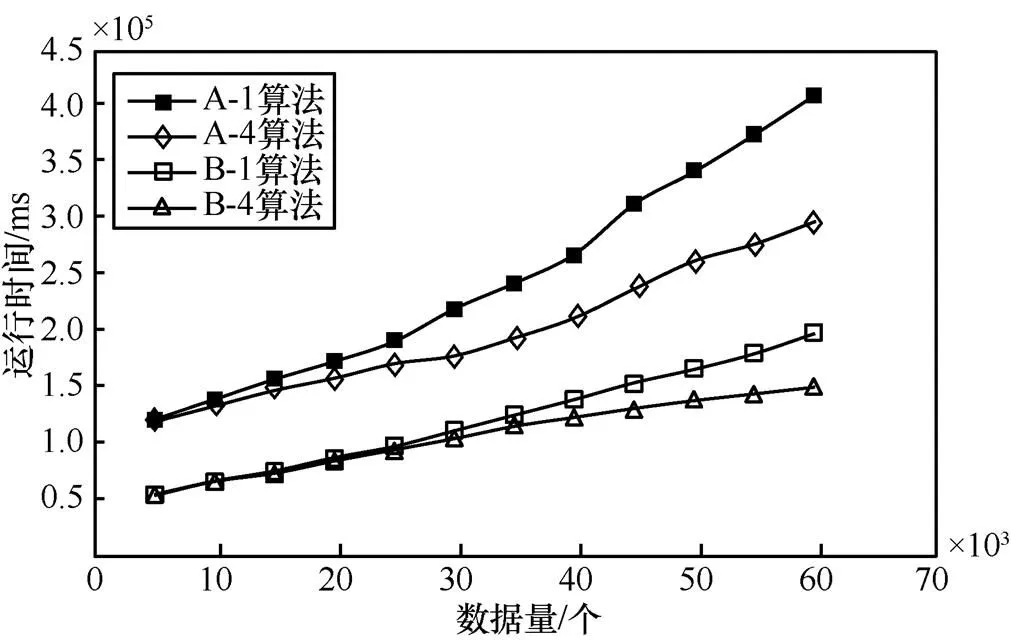
图2 算法运行时间

运行时间差值随数据变化情况如图3所示。由图3(a)可以看出，当系统启动4个子节点时A算法和B算法的运行时间比启动一个子节点时有显著减少，且随着数据量的增加，运行时间的减少量也在增加；由图3(b)可以看出，A算法相对于B算法在系统启动4个子节点时小于系统仅启动一个子节点时的运行时间增量（由于添加随机噪声造成的增量）。

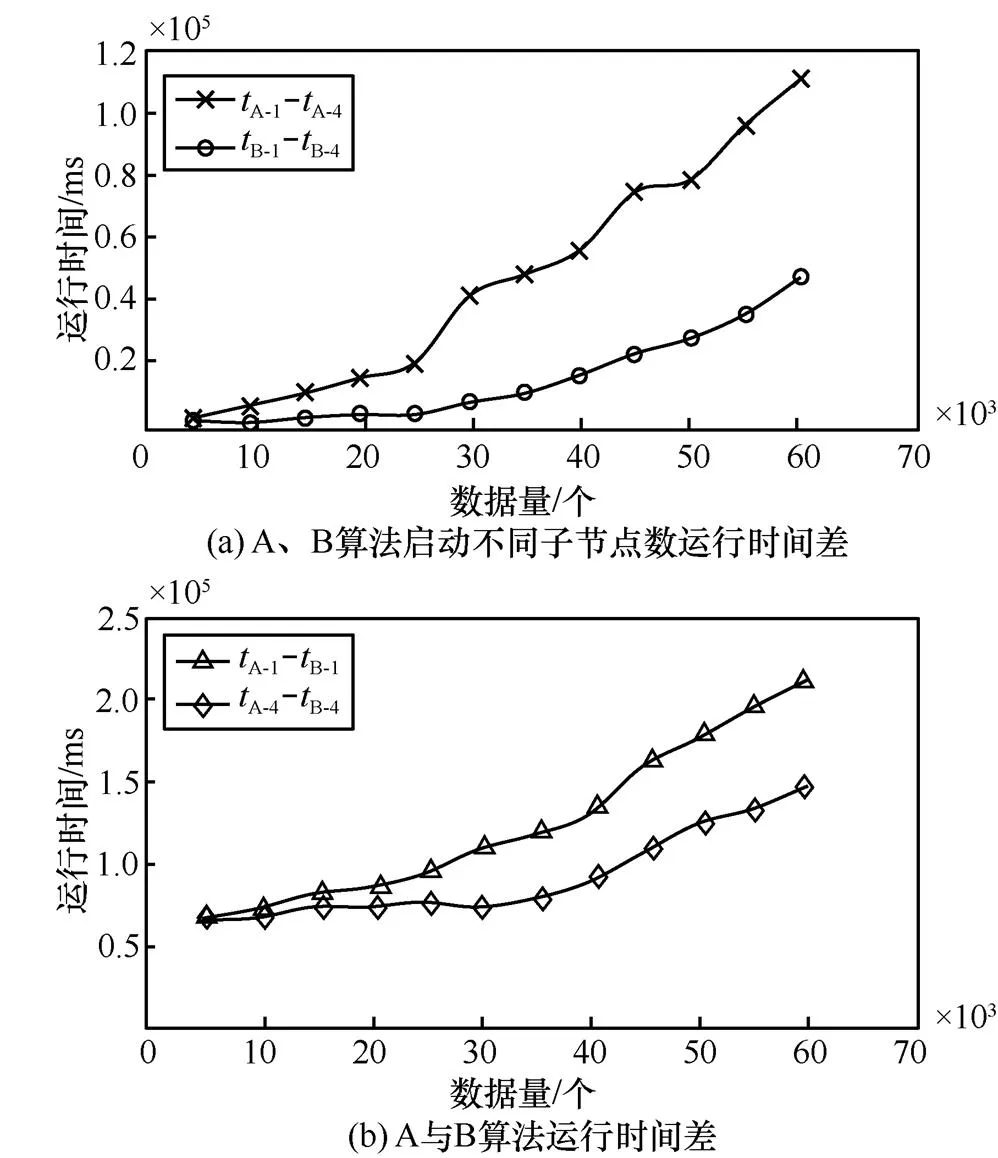
图3 运行时间差值随数据量变化情况

由此可以认为，本文所提算法能够使需要反复迭代的随机梯度下降算法在提供差分隐私保护的同时，在MapReduce框架下进行高效率的计算，并能够随计算节点的增加而提高算法的运行效率。同时，本文所提算法与SCS13算法和BST14算法在噪声添加方面采取了不同策略，如图4所示。

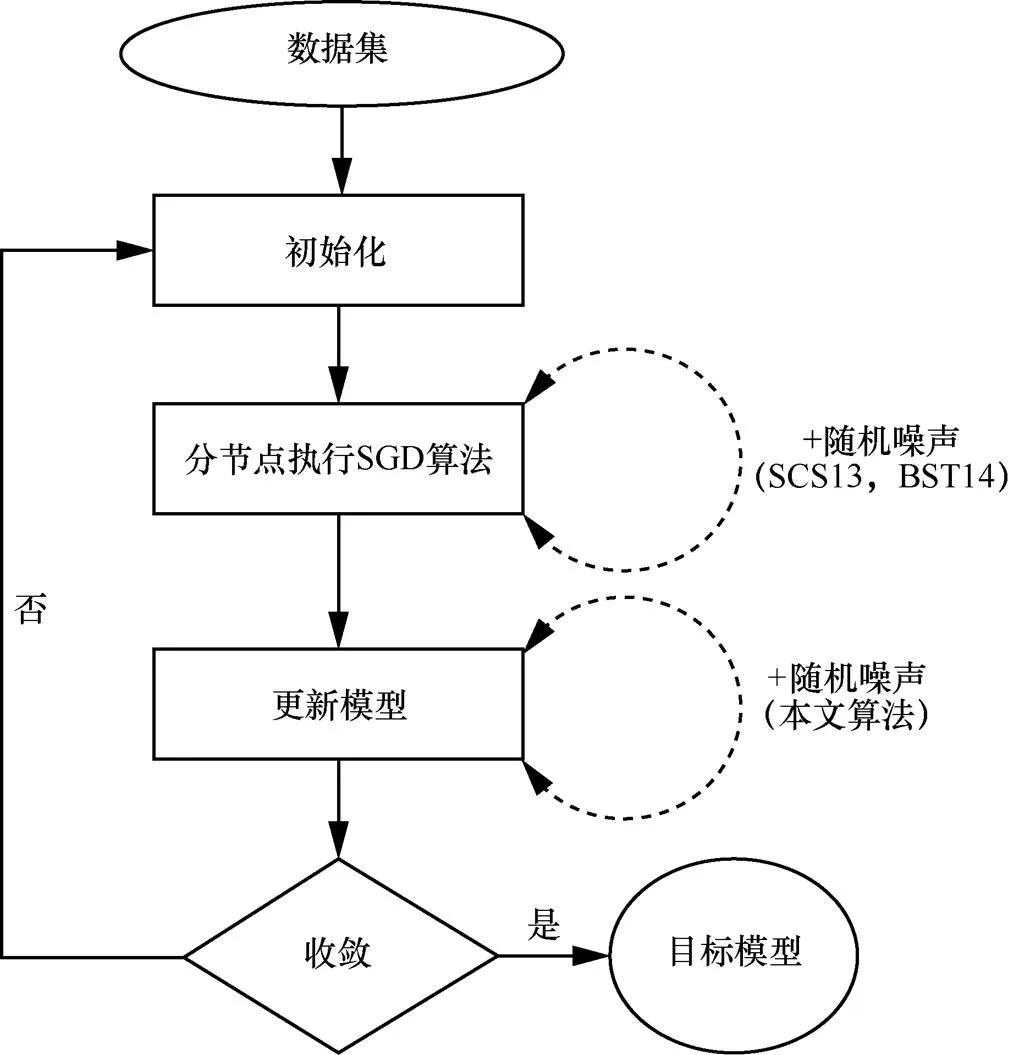
图4 各算法随机噪声添加位置示意

各算法运行时间对比如图5所示。由图5可知，本文所提算法在耗时上对比SCS13算法和BST14算法具有明显优势，且数据量越大优势越明显。

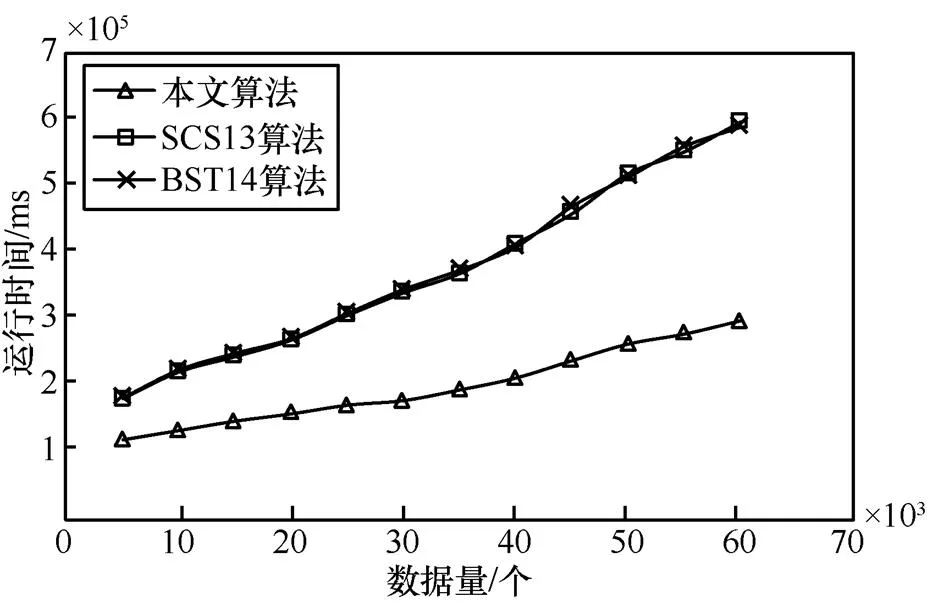
图5 各算法运行时间对比

4.2 算法可用性实验

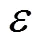
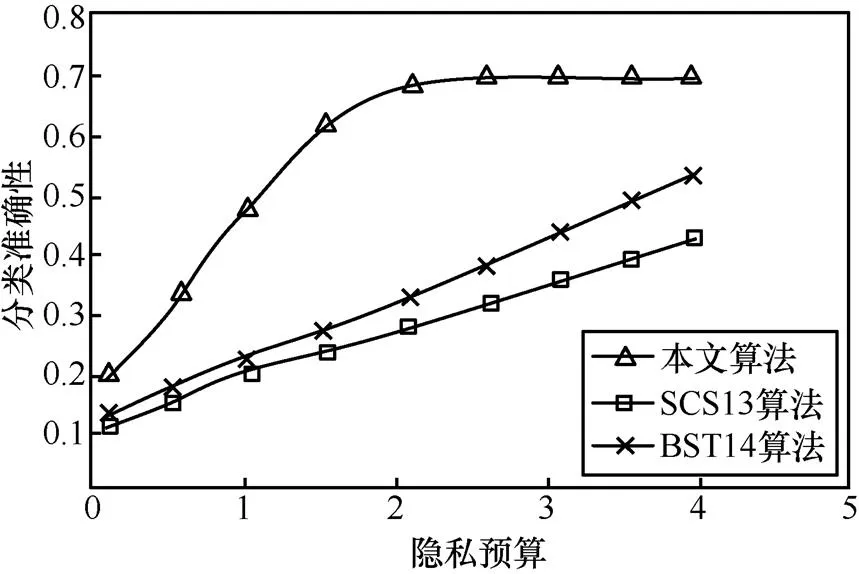
图6 各算法分类准确性随隐私预算变化情况

5 结束语

本文在MapReduce计算框架下，提出了一种能同时满足效率性与私密性的差分隐私—随机梯度下降新算法DP-SGD。该算法通过合理的计算资源分配与随机噪声添加策略，在满足差分隐私保护要求的同时，缓解了随机梯度下降算法因反复迭代在分布式计算框架下的通信开销，提高了算法的计算效率并保证了数据的可用性。下一步可进行以下2个方面工作：1) 在本文所提算法基础上，对算法中的参数设置方案进一步优化，分析各个参数在对算法效率性影响上的内在关系，进一步提高算法的效率；2) 研究算法中为满足差分隐私保护所需随机噪声量的最小值与数据量、迭代次数和目标模型合并方法之间的关系，减少因随机噪声的添加带来的算法在效率性与可用性上的负面影响。

[1] WU F, LI F G, KUMAR A, et al. Bolt-on differential privacy for scalable stochastic gradient descent-based analytics[C]//The 2017 ACM International Conference on Management of Data. 2017: 1307-1322.

[2] ABADI M, CHU A, GOODFELLOW I, et al. Deep learning with differential privacy[C]//The 2016 ACM SIGSAC Conference on Computer and Communications Security. 2016:308-318.

[3] ZHAO P, ZHANG T. Stochastic optimization with importance sampling[J]. Eprint Arxiv, 2015:1-9.

[4] SCHMIDT M, ROUX N L, BACH F. Erratum to: minimizing finite sums with the stochastic average gradient[J]. Mathematical Programming, 2016, 162(5): 1.

[5] MU Y, LIU W, LIU X, et al. Stochastic gradient made stable: a manifold propagation approach for large-scale optimization[J]. IEEE Transactions on Knowledge & Data Engineering, 2015, 29(2): 458-471.

[6] ZINKEVICH M, WEIMER M, SMOLA A J, et al. Parallelized stochastic gradient descent[C]//The Conference on Neural Information Processing Systems. 2011:2595-2603.

[7] 陈振宏, 兰艳艳, 郭嘉丰,等. 基于差异合并的分布式随机梯度下降算法[J]. 计算机学报, 2015, 38(10):2054-2063.

CHEN Z H,LAN Y Y,GUO J F, et al.Distributed stochastic gradient descent with discriminative aggregating[J].Chinese Journal of Computers, 2015, 38(10):2054-2063.

[8] ZHAO H, CANNY J F. Communication-efficient distributed stochastic gradient descent with butterfly mixing[D]. Berkeley, USA: University of California, 2012.

[9] SONG S, CHAUDHURI K, SARWATE A D. Stochastic gradient descent with differentially private updates[C]//Global conference on Signal and Information Processing (GlobalSIP).2013: 245-248.

[10] BASSILY R, THAKURTA A. Private empirical risk minimization: Efficient algorithms and tight error bounds[C]//2014 IEEE 55th Annual Symposium on Foundations of Computer Science (FOCS).2014: 464-473.

[11] DWORK C, MCSHERRY F, NISSIM K. Calibrating noise to sensitivity in private data analysis[J]. The VLDB Endowment, 2006, 7(8):637-648.

[12] DWORK C, ROTH A. The Algorithmic foundations of differential privacy[M]. Now Publishers Inc, 2014.

[13] CHAUDHURI K, MONTELEONI C, SARWATE A D. Differentially private empirical risk minimization[J]. Journal of Machine Learning Research, 2009, 12(2):1069-1109.

[14] 何贤芒, 王晓阳, 陈华辉,等. 差分隐私保护参数的选取研究[J]. 通信学报, 2015, 36(12):124-130.

HE X M,WANG X Y, CHEN H H, et al. Study on choosing the parameterin differential privacy[J].Journal on Communications, 2015, 36(12):124-130.

[15] MCSHERRY F D. Privacy integrated queries: an extensible platform for privacy-preserving data analysis[J].Communication of the ACM, 2010, 53(9):89-97.

Stochastic gradient descent algorithm preserving differential privacy in MapReduce framework

YU Yihan, FU Yu, WU Xiaoping

Department of Information Security, Naval University of Engineering, Wuhan 430033, China

Aiming at the contradiction between the efficiency and privacy of stochastic gradient descent algorithm in distributed computing environment, a stochastic gradient descent algorithm preserving differential privacy based on MapReduce was proposed. Based on the computing framework of MapReduce, the data were allocated randomly to each Map node and the Map tasks were started independently to execute the stochastic gradient descent algorithm. The Reduce tasks were appointed to update the model when the sub-target update models were meeting the update requirements, and to add Laplace random noise to achieve differential privacy protection. Based on the combinatorial features of differential privacy, the results of the algorithm is proved to be able to fulfill ε-differentially private. The experimental results show that the algorithm has obvious efficiency advantage and good data availability.

machine learning, stochastic gradient descent, MapReduce, differential privacy preserving, Laplace mechanism

TP301

10.11959/j.issn.1000-436x.2018013

俞艺涵（1992-），男，浙江金华人，海军工程大学博士生，主要研究方向为信息系统安全、隐私保护等。