数据流的集成分类方法研究

潘科学

（四川大学计算机学院，成都 610065）

0 引言

随着电信、网络等信息技术的迅速发展、时序应用不断涌现，其中出现了大量的数据流，如电信通话记录、网上购物交易记录、股票交易记录、文星探测和天文观测数据等。这些数据流中隐含着丰富的、有价值的信息亟待挖掘。然而与传统数据形式不同，数据流具有海量、实时、有序、动态等特点，若采用传统的数据挖掘模型，则会丢失大量有价值的信息，而且会耗费大量的时间、空间，因此对数据流的分类成为机具挑战的工作[1]。

为适应数据流海量、实时、动态等特点、分类模型应具有良好的时空性能、且在抗噪性、适应性方面也具有良好表现。H.X.Wang等[2]证明了与单模型相比，集成分类方法在分类性能尤其是抗噪性能方面具有一定的优势。诸多研究也表明构造一系列简单的分类器比建立一个复杂的但分类器更加简单可行，可以说，集成分类方法是一种有效的数据流分类方法。

针对数据流的特点，近年来学术界涌现出大量针对数据流集成分类的工作，Wang[3]等人提出了在数据流上的集成分类器，它把数据流分为不同的时间段，利用每一时段的训练数据学习一个分类器，针对每一个分类模型，利用最新到达的数据决定他的权重，最后用多个分类器共同预测未来数据，与单分类器相比，集成分类器有更高的分类准确率。此后，Street[4]等人提出了SEA算法，它采用启发式策略根据正确率和数据特征取代表现较差的分类器，以提高分类性能。Yu等人[5]使用集成学习方法对多标签数据分类问题进行研究，并最终将所提出模型在生物蛋白功能判定领域进行应用，通过实验验证了有效性。Li等人[6]针对集成学习模型中的结果融合部分进行研究，提出一种基于权值的分类结果选择方法（DCE.cc），通过对不同个体分离输出结果进行判定，将个体分类器赋予不同的权重，并根据权重，对分类结果进行针对性汇总，从而避免误分类模型对整体分类结果的影响。Omid等人针对数据流的动态性，将数据流划分成不同的数据块，根据模型在各数据块的表现判断概念漂移是否发生，通过更新模型提升分类精度[7]。Bieft等对近年来主流的数据流集成分类方法机型总结和分类[8]。

综上所述，对于数据流的集成分类仍处于研究阶段，现存的方法人存在各种各样的弊端，如分类器组合、样本选取、基分类器独立性等。基于此，本文设计一种针对数据流的集成学习方法，通过与单一模型进行比较，发现集成模型确实有着单一模型不能比拟的性能。

1 集成学习

1.1 集成学习理论

集成学习是使用一系列弱学习器进行学习，并使用某种规则把各个学习结果进行整合从而获得比单个学习器更好的学习效果的一种机器学习方法。它的思想非常简单，集合多个模型的能力，达到“三个臭皮匠，赛过诸葛亮”的效果。

将一组学习方式、学习能力不同的同质或异质分类模型进行组合而获得集成分类模型，其直观感觉是所构成的集成模型分类性能应该介于最好的单模型分类器与最差的分类器之间。但是许多学者通过大量实验证明，集成分类模型的学习性能要优于最好的单体分类器[9]。首先，从统计的角度来看，由于学习任务的假设空间往往很大，可能有多个假设在训练集达到同等性能，此时若使用单学习器可能会因误选而导致泛化性能不佳，结合众多策略则会减少这一风险；第二，从计算角度来看，学习算法往往会陷入局部极小，有的局部极小点所对应的泛化性能可能很糟糕，而通过多次运行之后进行结合，可降低陷入局部极小点的风险；第三，从表示的角度来看，某些学习任务的真实假设可能不在当前学习算法所考虑的假设空间中，此时若使用单学习器肯定无效，而通过结合多个学习器，由于相应假设空间有所扩大，有可能学的更好的近似结果。图1为更直观的示意图：

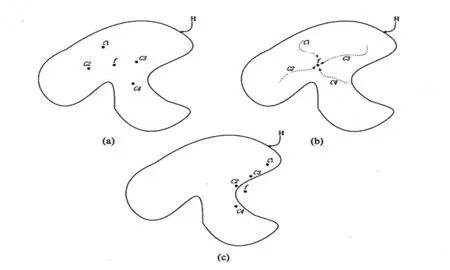
图1 集成学习分析的三种角度

1.2 集成策略

集成学习结合策略主要分为两类：Averaging meth⁃ods和 Boosting methods。

●Averaging methods核心是引入随机（对样本、特征属性随机取样）学习产生多个独立的模型，然后平均所有模型的预测值。一般而言，这种方法，会减小方差（variance），不太会过拟合。主要包括bagging、RF。

●Boosting methods逐步加强方法，该方法集合学习多个模型，提高模型的准确率。不同的是，它是基于前面模型的训练结果（误差），生成新的模型，从而减小偏差（bias）。一般而言，这种方法会比上者的准确率高一点，但是也不是绝对的。它的缺点是有过拟合的风险，另外，由于它每个模型是“序列化”（有前后关系）产生的，不易并行化。它的代表是AdaBoost、GDBT。

Bagging:Bagging在原始样本中随机抽样获取子集，用随机抽样的子集训练基学习器（base_estimator），然后对每个基学习器的结果求平均，最终得到的预测值。随机获取样本子集的方法有很多中，最常用的是有放回抽样的booststrap，也可以是不放回的抽样。基学习器可以是相同的模型，也可以是不同的，一般使用的是同一种基学习器，最常用的是DT决策树。由于bagging提供了一种降低方差（variance）的方式，所以一般会使用易受样本扰动的分类器。

随机森林：用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。

AdaBoost：AdaBoost是一种 Boosting方法，与 Bag⁃ging不同的是，AdaBoost中不同的子模型必须是串行训练获得的，每个新的子模型都是根据已训练出的模型性能来进行训练的，而且Boosting算法中基学习器为弱学习器。AdaBoost中每个训练样本都有一个权重且每次迭代生成新的子模型使用的训练数据都相同，但是样本的权重会不一样。AdaBoost会根据当前的错误率，增大错误样本权重，减小正确样本权重的原则更新每个样本的权重。不断重复训练和调整权重，直到训练错误率或弱学习器的个数满足用户指定的值为止。

2 基于权重的集成学习方法

集成分类方法是目前数据流分类的一种主要方法，通过在不同数据块上构建分类器并对这些分类器进行组合，以达到比单一分类器性能更好的目标。本节基于权重集成方法设计了一个集成分类模型，研究表明，基于权重集成的方法[10]具有以下优点：

（1）利用多个历史数据块的信息用于当前数据的测试。

（2）最终的决策是基于多个历史数据块训练的结果，一定程度上减弱了噪声数据对分类精度的影响。

2.1 基分类器选取

传统分类方法都已应用于数据流集成分类方法中，本文模型在集成决策树、KNN、SOM、SVM等多个分类方法基础上，引入朴素贝叶斯提升模型的抗噪性能。

朴素贝叶斯是一种基于统计理论的分类方法，很多文献将其引入决策树的叶子结点，用以代替传统的最大类预测方法[11-12]，提升抗噪性能。这是因为朴素贝叶斯为增量式学习方法，对新数据不敏感，从而提升了模型的抗噪性能。因此本文集成方法引入朴素贝叶斯以提升分类性能。

2.2 基于权重的集成方法

本文模型的主要思想为：记数据流中t时刻到达的数据块为Dt，基于权重集成分类方法选择一种学习方法（如VFDT[13]，SVM，DT等）对每个数据块进行独立学习，得到n个基分类器fi=F（Di）,并通过不同的策略对基分类器赋权值，得到集成分类器few。图2为基于权重的集成分类方法示意图。

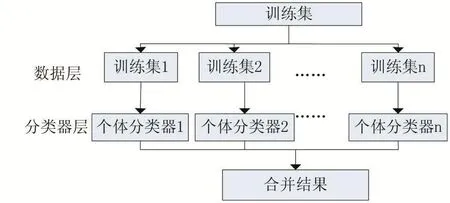
图2 集成模型框架

基于权重的集成算法：

3 实验结果

3.1 数据集

数据集分为两类：人工数据集、真实数据集。

人工数据集:

LED漂移数据集，MOA封装了LED数据集的生成器，即针对属性维是24的LED数据集版本，最多可以设置7维属性漂移，同时可以设置不同比例的噪音。

Wave数据集含有三个类标签，根据含有24个连续属性或40个连续属性形成Wave21和Wave40两个版本，常被作为检测数据流分类算法性能的典型数据集。

真实数据集：

Forest Covertype数据集，源于UCI数据集，它是关于森林覆盖方面的数据库。该数据库含有7个类标签，54维属性，共581012个实例。

Electricity数据集，该数据集来自澳大利亚新南部威尔士电力市场。该数据集的描述为：电力市场的电价是变化的，反映了市场的供求关系，电价每五分钟调整一次。该数据集包含45312个实例，两个类标签up和down，以及7维属性。

3.2 实验结果

本文实验通过将集成模型与单一分类器进行比较，对比标准采用分类常用指标accuracy，由于是集成分类模型，实验时将数据分成连续大小相同的数据块，这样做也在一定程度上适应了数据流的动态变化特性。图2、图3为本文模型和单一分类模型在真实数据集上的Acc值。图3、图2为本文模型和单一分类模型在人工数据集上的Acc值。其中纵坐标为Acc值，横坐标为不同窗口大小。由图可见。集成模型比单一分类模型的准确度要高。这是因为通过调整集成模型基分类器的权值，选取分类结果较好的分类器，从而使得分类准确度较高。

4 结语

数据流分类为目前比较热门的研究方向，由于数据流自身的海量实时动态等特点，使得如何在有限的时间和空间限制内实现较高的准确度成为数据流分类的巨大的挑战。本文通过构建集成分类器对数据流进行分类，并与单一模型作比较，实验结果显示集成模型的分类准确度比单模型较优。

数据流的动态性为数据流的核心特点之一，动态性主要体现为概念漂移的产生，概念漂移即数据分布或类别分布发生变化，使得当前模型不在适应当前数据集，如不能及时更新模型，则模型性能则会急剧下降，此外检测概念漂移的产生也是数据流分类的核心难题。

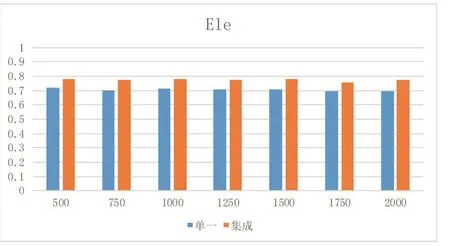
图2 单一和集成模型在ele上的Acc

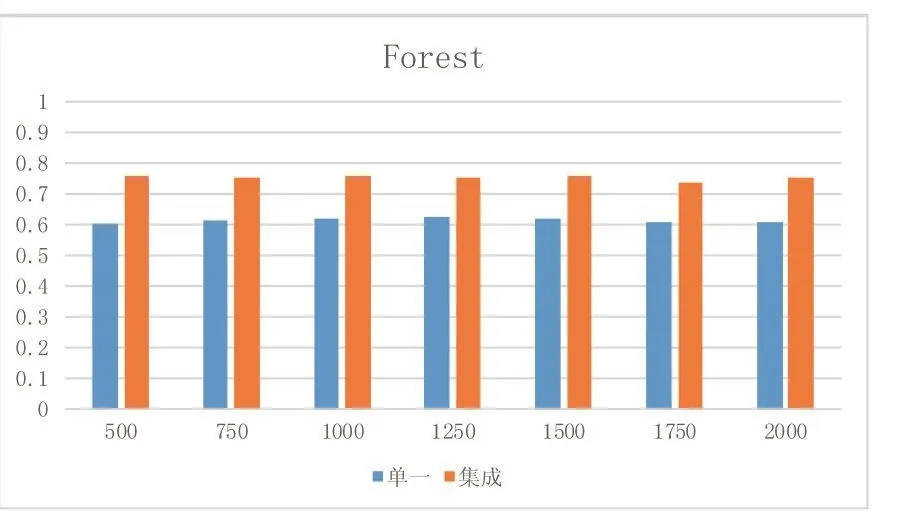
图3 单一和集成模型在Forest上的Acc

图4 单一和集成模型在LED上的Acc

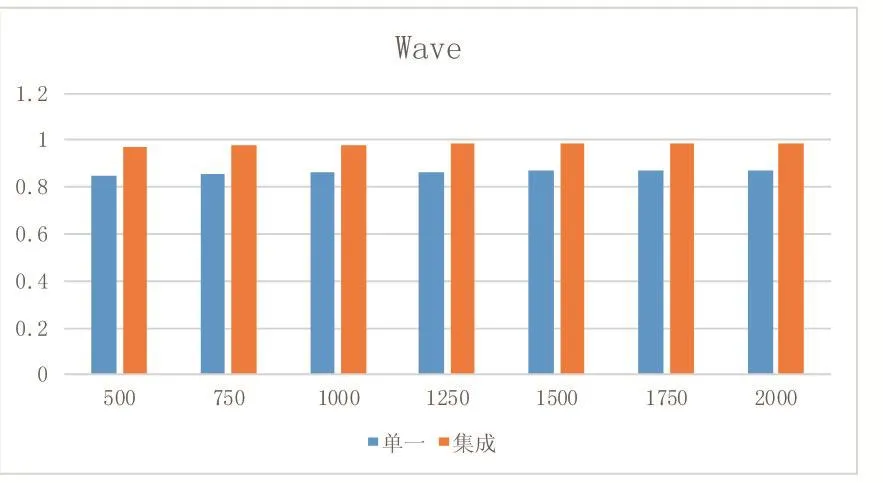
图5 单一和集成模型在Wave上的Acc

[1]Zhang P.，Gao B.J.，Liu P.，et a1.A Framework for Application-Driven Classification of Data Streams[J].Neurocomputing，2012，92（0）：170-182．

[2]H X Wang,W Fan,P S Yu，J W Han.Mining Concept-Drifting Data Streams using Ensemble Classifiers[C].

[3]Wang,H.Fan,Yu.P.S.,et al.,2003.Mining Concept-Drifting Data Streams Using Ensemble Classifiers.Proc.9th ACM AIGKDD Int.Conf.on Knowledge Discovery and Data Mining,p.226-235.

[4]Street W N,Kim Y S.A Streaming Ensemble Algorithm（SEA）for Large-Scale Classification[C].Proceedings of the S eventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM,2001:377-382.

[5]Yu G.，Domeniconi C.，Rangwala H．，et a1.Transductive Multi-Label Ensemble Classification for Protein Function Prediction[C]．Proceedings of the 18th ACM SIGKDD Internation81 Conference on Knowledge di scovery and Data Mining，Bei Jing，China，Aug12-16，2012：1077-1085．

[6]Li L.J．，Zou B.，Hu Q.H．，et a1.Dynamic Classifier Ensemble Using Classification Confidence[J].Neurocomputing，2013，99（1）：581-591．

[7]Omid,Ali.An Ensemble Method for Data Stream Classification in the Presence of Concept Drift.Reversion Accepted Apr.15.2015.

[8]Heitor Murilo Gomes,Jean Paul Barddal,Fabr'ıcio Enembreck,and Albert Bifet.2017.A Survey on Ensemble learning for data stream Classification.ACM Comput.Surv.50,2,Article 23（March 2017）,36 pages.

[9]周志华.机器学习

[10]胡学刚，李培培等.数据流分类.

[11]J Gama,P Medas,P Rodrigues.Concept Drift in Decision Trees Learning from Data Stream[C].In:Proceedings of 4th European Symposiumon Intelligent Technology and Their Implemention on Smart Adaptive Systems.pp218-225,2004.

[12]J Gama,R Fernandes,and R Rocha.Decision Trees for Mining Data Streams[J].Journal of Intelligent Data Analysis（10）,23-45,2006.

[13]Domingos P,Hulten G.Mining High-Speed Data Streams[C].Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM,2000:71-80.