核最小模最小平方误差方法医学图像识别算法

夏开建，靳勇

1.苏州大学附属常熟医院（常熟市第一人民医院） 信息科，江苏 常熟 215500；2.常熟理工学院 计算机工程与科学学院，江苏 常熟 215500

引言

最小平方误差方法（Minimum Squared Error，MSE）[1-3]由于良好的分类性能广受人们重视，该方法试图通过对训练样本的训练找到线性判别函数中有效的投影向量w，用以对测试样本进行分类。但是现实中有许多问题都是非线性可分的，例如像医学目标识别等问题[4-6]中由于角度、噪声、蠕动等不同所引起的医学目标图像的差异造成医学器官图像的分布往往是非线性的和复杂的。

核技术[7-10]的使用，使得支持向量机（Support Vector Machine，SVM）在模式识别领域获得了很大的成功。其思想是通过非线性映射将输入空间变换到一个高维特征空间F中，映射后的向量可以包含原样本的非线性的信息，而这种非线性映射是通过定义适当的内积函数实现的。它成功的避免了在高维的特征空间中广义线性鉴别函数存在的“维数灾难”问题，提供了一种有效抽取样本的非线性特征的方法。主分量分析（Principal Component Analysis，PCA）是线性特征抽取的最为重要的技术之一，目前仍然广泛地应用在医学目标图像等图像识别领域。

本文在传统的MSE的基础上引入核技术，提出了一种基于核的最小模最小平方误差方法（Kernel Minimal Mean Square Error，KMNMSE），该方法有效的解决了传统的MSE方法存在的非线性可分问题。另外，针对传统的MSE方法中的投影向量可能存在“超定”的问题，引入了广义逆矩阵的概念，并给出了其求解方法。在此基础上，又提出了一种一般的MNMSE分类器模型。之后，鉴于核主分量分析（Kernel Principal Component Analysis，KPCA）方法在特征抽取中的成功应用，本文提出了一种基于KPCA与MNMSE分类器的一种新的医学目标识别方法，该方法不仅达到了对核样本向量降维的目的，而且在核样本空间中在最小均方差意义下给出了模式样本的最优表示，同时该方法也再次证明了MNMSE分类器的有效性。最后，在医学图像库上的实验结果验证了本文所提出的理论与方法的有效性。

1 最小平方误差方法

假设有n个m维的样本x1,x2…xn∈Rm当中包含两类不同的样本，其中n1个样本属于ω1，n2个样本属于ω2。我们要通过这n个训练样本来寻找一个投影向量w，用于下面的线性判别函数：

在两类问题中，如果判别函数的值g(x)＞0则x∈ω1；如果 g(x)＜0 则 x∈ω2。

定义y=[x1]T×s(x)作为x标准化的向量。其中，x∈ω1时s(x)=1；x∈ω2时 s(x)=-1。

再定义一个阈值向量b=[b1K bn]T，这样线性判别函数方程组就可以用矩阵简化表示，我们的目标也就转化为寻找向量a使得：

如果Y是非奇异的，我们立刻可以得到a的解a=Y-1b。但是Y通常是一个长方形的矩阵，当行数大于列数时方程组的个数多于未知数的个数，a是超定的，通常没有精确的解。定义误差向量e=Ya-b，最小平方误差的方法就是通过定义如下的最小化误差平方和的准则函数，使得误差向量的长度的平方最小化。

一旦a得出后，式(1)也可以推出，[w,w0]T=a。在YTY非奇异时a可以通过以下公式求得：

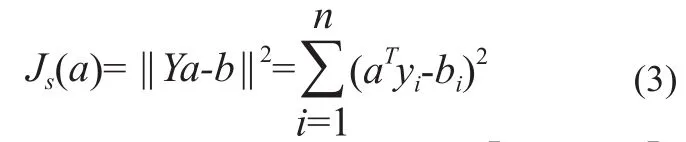
YTY在医学目标识别等高维小样本问题中通常是非奇异的，这种情况下，不论a是否是超定的，式(3)的判别函数（MSE）的解总是存在。

2 基于核的最小模最小平方误差方法（KMNMSE）

核方法的基本思想就是要解决非线性可分的问题[11-13]。首先将原始训练样本通过一个非线性映射映射到某一高维（可能是无限维）特征空间F中，然后在F中执行线性鉴别分析方法。由于特征空间F的维数非常高甚至是无穷维，为了避免直接显式地处理映射后的样本，引入支持向量机中的核函数。这些核函数可以计算某些特征空间上的内积，即k(x,y )=＜(x)。在支持向量机中常用的核函数有高斯 RBF 核函数 k(x,y)=exp(-‖x -y‖2/σ)，多项式核函数k(x,y)=(x×y+c)d，其中σ、c和d都是常数。因此，我们在经典的最小平方误差方法中引入核的概念以解决其存在的非线性可分问题[14-16]。

将n个训练样本x1,x2,…, xn∈Rm通过一个非线性映射映射到特征空间F中，对应的训练样本变为o(x1),…,(Xn)，相应的判别函数变为:

相应的向量v由投影后的n个样本训练获得，根据再生核理论解向量v一定位于(x1),…,(xn)张成的空间内。既存在系数向量 α=(α1,…,αN)T∈RN，满足 ：

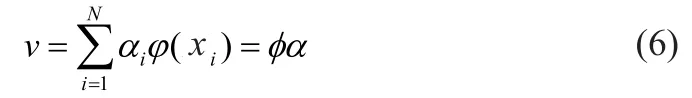
定义1ζk=[k(x1,xk),…,k(xN,xk)]T,称ζk为核样本向量（对应于原始输入样本xk），称α为核鉴别向量。

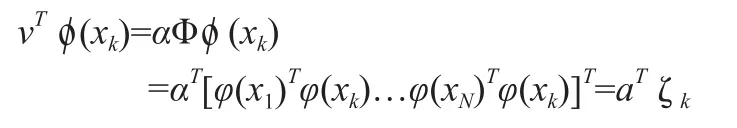
这样我们的判别函数可以改写为如下的形式：

与传统的MSE方法类似，我们对判别函数进行简化：

其中，H是由标准化后的核样本向量hi=[ζi1]T×s(x)作为行向量的矩阵。同样x∈ω1时s(x)=1；x∈ω2时s(x)=-1。α,v0也与u有如下的关系：

定义如下的核最小化误差平方和的准则函数（Kernel Minimal Square Error，KMSE），使得核样本向量误差向量的长度的平方最

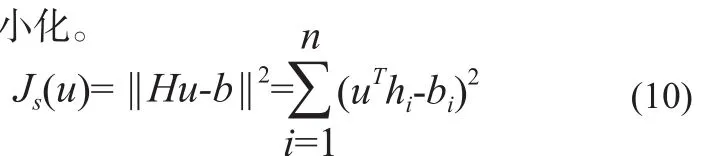
在HTH非奇异时u可以通过以下公式求得：

我们定义H的广义逆矩阵（伪逆矩阵[]）H+=(HTH)-1HT，不论H非奇异或奇异，(9)式的u是否超定（没有精确的解），KMSE的解总是存在的。将H+定义为如下形式：

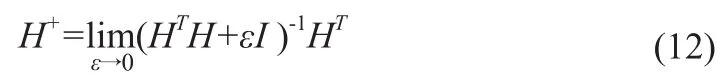
可以证明这个极限总是存在的，u=H+b就是式(9)判别函数的一个解。我们称之为KMNMSE。

求得H+之后，我们要找的投影向量u也就得到了u=H+b。那么在接受到一个测试样本后，这种KMNMSE又是如何判别其所属类别呢？

假设x为一输入的测试样本向量，识别过程按如下步骤进行：① 选择核函数，依照先前所述的方法转换为核样本向量ζ=[k(x1,x),…,k(xn,x)]T；② 得到此核样本向量的增广向量Γ=[ζT1]T；③ 将得到的增广向量在求得的u向量上投影 λ=uTΓ,λ=1 则 x∈ω1；λ=-1 则 x∈ω2。

3 基于MNMSE方法的分类器及医学目标识别

通过上一节的讨论我们可以发现KMNMSE不仅具有良好的性质，而且简单易行。同时我们也能够根据以上的讨论得出基于MNMSE方法的分类器一般模型判别函数：

其中，y为原样本向量x经过各种变换后的p维样本向量；H+为如上所述的广义逆矩阵；b为定义的任意正值的裕值向量；d为p+1维的增广向量。

以上我们讨论的是两类模式问题，但是在像医学目标识别等模式识别问题中一般都是多类别问题，下面我们将两类问题推广为多类。

假设有c个模式类标识为ω1K ωc，我们在进行第3节的训练过程的时候，将属于ωi的样本和不属于ωi的样本看作是两类不同的样本。这样对于每一类训练样本我们都可以得到一个相应的投影向量ui=Hi+b，定义投影矩阵U由这一组投影向量组成，U=[u1…uc]。

这样在识别过程中我们可以将测试样本的核样本向量在U上投影：

可以看出这里的L=[λ1…λc]T，若L中的元素λi=1则此测试样本就归于ωi。

主分量分析是线性特征抽取的最为重要的技术之一，目前仍然广泛地应用在医学图像融合等图像识别领域，其本质上在最小均方差意义下给出了模式样本的最优表示。KPCA是将K-L变换（主分量分析）推广到用来抽取非线性特征。我们首先用KPCA的方法来抽取出对应原始样本的特征向量用以代表原始样本，然后用MNNSE分类器对这些对应原始样本向量的特征向量进行分类。

KPCA的基本思想是将由映射后的数据o(xi)得到的总体协方差矩阵对 角化。为此，需要对下式的特征方程求解。

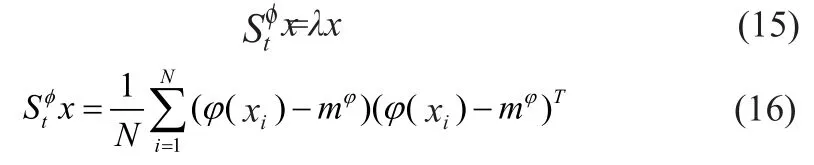
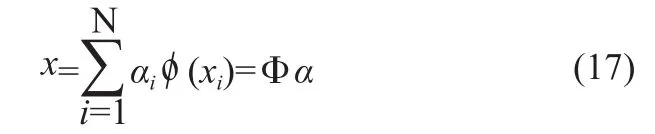
这样我们得到N个训练样本的p维特征向量，然后用这N个p维向量作为MNMSE分类器的输入向量y，如上节所述对对分类器进行训练得到U。在对测试样本进行分类时，同样先对测试样本进行核主分量分析得到相应的p维特征向量Γ，再用MNMSE分类器进行分类识别。

4 实验结果及分析

本文利用采集到的1024幅包括正常肺组织、良性肺结节和肝癌3种肺部CT图像，以及514幅包括正常甲状腺与甲状腺癌的两种甲状腺CT图像进行实验，所有图像类型均经过临床医师确诊，图像类型均为JPEG格式，大小为768×576，采集于同一台CT仪器。使用欧式距离进行医学图像的分类识别。在Window 7系统下，使用MATLAB R2007b开发环境，实现了医学图像识别的原型算法。

4.1 评价准则

对于医学图像识别问题，识别结果会产生不同的两种结果。其中，TP表示正确识别的样本个数，TN表示正确识别的阴性样本个数。准确率（Accuacy）表示正确分类的样本数占所有分类样本的比例，如式(18)所示。

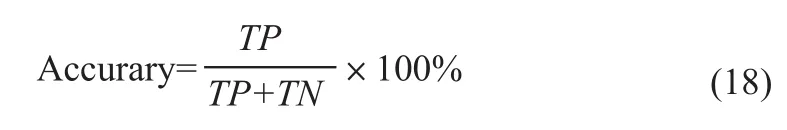
4.2 肺CT图像识别

本试验的目的是验证本提出的KMNMSE方法的有效性。在试验中，通过对不同类别，不同样本数的肺CT图像提取的特征，用KMNMSE方法进行分类识别。根据采集的图像共设计7组不同的样本。对各组样本结果数据分析，根据前面的分析，首先计算RN空间上的核特征向量ζk(k=1,…,200)，然后由ζk(k=1,…,200)进行训练计算出投影矩阵U，然后计算得到256个测试样本的核样本向量进行分类，识别率，见表1。此外，我们还做了该方法和传统MSE方法识别率和时间的比较。

表1 不同算法在不同分组数据上的识别准确率对比

通过准备率对比可以看出，本文提出KMNMSE方法利用核方法的高效特征计算的优势，与PCA特征向量相互作用，具有较高的识别率。本文方法通过非线性映射将输入空间变换到一个高维特征空间F中，映射后的向量可以包含原样本的非线性的信息，因此提升了识别的准确性。

在识别率提高的基础上，对算法运行时间进行测试（表2）。本文算法构造特征空间所用时间明显小于传统算法，而识别时间基本相同。原因是核方法处理后每一块的维数降低，对每一块进行传统PCA算法时间明显减少，导致构造特征空间的时间减少。由于两种算法识别部分基本相同，识别时间相差不多。最终改进算法运行总时间优于传统算法。

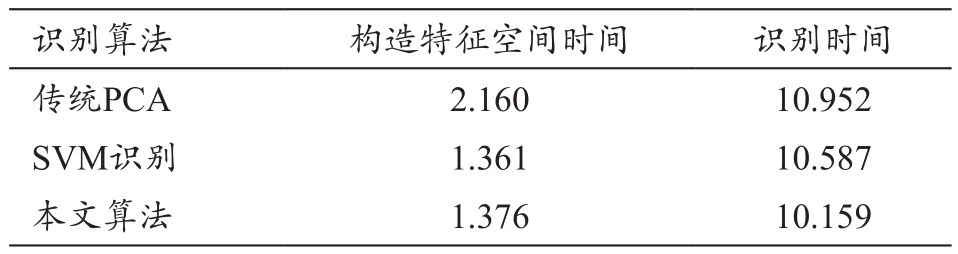
表2 不同算法的性能对比（s）

4.3 甲状腺CT图像识别

本实验利用医院获取的大量甲状腺图片，利用本文提出的特征提取方法进行提取，然后利用基于核主分量分析与MNMSE分类器的医学目标识别方法分类识别（图1）。

图1 甲状腺CT图像

本文提出的医学图像识别方法对甲状腺CT图像进行分类的结果，见图2。从图中可以看出，利用本文提出的甲状腺PCA特征的提取方法可以对甲状腺的正异常很好地分类，分类准确率为100%。

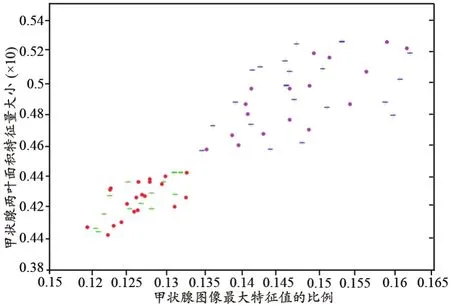
图2 本文算法的分类结果

5 结论

本试验在对人体甲状腺和肺部CT图像及其病理研究的基础上，针对其病变特点，提出将基于核主分量分析与MNMSE分类器的医学目标识别方法用于甲状腺（肺部）状态进行分类识别，利用核主分量分析提出的稳定特征，为分类的成功提供了良好的基础。然后，根据所提取的特征采用MNMSE分类器对甲状腺（肺部）的正异常进行分类。经仿真结果验证，使用本文中提出的这两个特征对甲状腺（肺部）的正异常可以取得较好的分类效果，且具有一定的准确性、可靠性和实用性，较好地实现了甲状腺的计算机辅助诊断，为医生的临床诊断提供一定的帮助。

[1]朱旗.基于最小平方误差的人脸特征抽取与分类算法研究[D].哈尔滨:哈尔滨工业大学,2014.

[2]王禹.基于线性回归分析的特征抽取及分类应用研究[D].扬州:扬州大学,2016.

[3]单宝堂,沈庭芝,崔玉红,等.预估计最小平方误差初始值方法改善交替映射算法性能[J].北京理工大学学报,2007,27(5):436-440.

[4]许建华,张学工,李衍达.最小平方误差算法的正则化核形式[J].自动化学报,2004,30(1):27-36.

[5]胡正平,彭燕,赵淑欢.非最小平方误差局部-全局加权融合的稀疏表示遮挡人脸识别[J].模式识别与人工智能,2015,28(7):633-640.

[6]Yang Y,Blum RS.MIMO radar waveform design based on mutual information and minimum mean-square error estimation[J].IEEE T Aero Elec Sys,2007,43(1):330-343.

[7]Davis B,Lorenzen P,Joshi S.Large deformation minimum mean squared error template estimation for computational anatomy[J].IEEE T Aero Elec Sys,2004(1):173-176.

[8]Wang J,Zhang Y,Cao H,et al.Dimension reduction method of independent component analysis for process monitoring based on minimum mean square error[J].J Process Contr,2012,22(2):477-487.

[9]Zhang L,Li X,Zhang D.Image denoising and zooming under the linear minimum mean square-error estimation framework[J].Image Processing Iet,2012,6(3):273-283.

[10]Lee J,Sankar R.Theoretical derivation of minimum mean square error of RBF based equalizer[J].IEEE Singal Proc Let,2007:1613-1625.

[11]温云磊,王元全,王怀彬.基于L0二阶偏导最小化和核回归模型的图像去噪方法[J].天津理工大学学报,2015,31(3):16-21.

[12]刘宇.基于水平集方法和模糊模型的医学图像分割算法研究[D].长春:吉林大学,2016.

[13]胡正平,彭燕,赵淑欢.非最小平方误差局部——全局加权融合的稀疏表示遮挡人脸识别[J].模式识别与人工智能,2015,28(7):633-640.

[14]Xia KJ,Wang JQ,Wu Y.Robust Alzheimer disease classification based on feature integration fusion model for magnetic[J].J Med Imag Health,7(6):1171-1176.

[15]Xia KJ,Wang JQ,Cai J.A novel medical image enhancement algorithm based on improvement correction strategy in wavelet transform domain[J].Cluster Comput,2017,(10):1-9.

[16]Xia KJ,Wu Y,Ren XG,et al.Research in clustering algorithm for diseases analysis[J].J Networks,2013,8(7):123-129.