对流层散射信道钟差预报模型*

胡邓华，王 洁，刘继业

0 引 言

时间同步技术在卫星导航定位系统、电力系统等分布式系统中应用广泛[1-2]。时钟校准是本地时间同步设备利用接收到的标准时间信号校准本地时间频率源的过程，是时间同步的基础。时钟校准能否正常顺利进行，决定着时间同步能否顺利建立。目前，时钟校准一般采用时间间隔计数器或鉴相器等设备测量本地时间频率源和收到的标准时钟信号之间的钟差，根据钟差控制本地频率源，最终达到时间同步的目的[3-4]。

目前，在距离较远的分布式系统中，传递时间信号的方式有微波传递、卫星传递以及对流层散射传递等[5]。传递过程中，无线电波不可避免地会受到外界因素的影响，一定程度上造成时钟校准不能正常连续进行。

为增加分布式系统中时间同步的稳定性和抗干扰性，本文将钟差预报技术引入时钟校准过程中。当时钟校准系统无法获取校准所需时钟信号时，利用一定算法结合已测钟差，对未来时段校准所需钟差进行预报，结合预报结果继续控制频率源，从而保证系统的正常连续进行。钟差预报技术在时间同步系统中应用广泛，是时间同步系统出现异常或无法实时获得钟差情况下能够正常工作的重要保障。钟差预报是一类针对钟差数据的时间序列预报。卫星钟差序列一般具有非严格单调性，即在不发生粗差的前提下，一段时间内钟差数据一般呈现大致增加或者减小的整体趋势，且钟差数据是一类精度很高的时间序列数据，变化较慢。目前，国内外学者针对钟差预报进行了广泛研究。2005年，崔先强提出了运用灰色系统理论进行钟差预报，选用四颗GPS星钟差数据建立了灰色预报模型，并分别进行了短期和长期钟差预报。结果表明，灰色模型的短期钟差预报精度与二阶多项式模型相当，长期预报精度比二阶多项式预报精度高[6]。徐波等人提出了基于多项式和泛函网络相结合的预报方法，采用泛函网络拟合多项式拟合残差，得出了该方法精度优于 IGU P（IGS Ultra-Rapid Predicted）星历的结论[7-8]。2013年，季利鹏等人在多项式模型的基础上，利用泛函网络（Functional Networks，FN）理论对钟差随机项和周期项分别建模，并将该方法与其他方法进行对比分析，得出了该方法能够减小中长期钟差预报误差的结论[9]。2014年，席超等人在差分平稳化处理钟差数据的基础上，建立了基于自回归滑动平均ARMA模型的长期钟差预报模型，预报了时长为90天的钟差情况，通过实例数据验证了该算法进行长期预报的有效性[10]。2014年，王国成等人建立了基于径向基函数神经网络的短期钟差预报模型，获得了Ins/d（d表示天（day））的预报精度[11]。此外，雷雨等人建立了基于小波变换和最小二乘-支持向量机（Least Square Support Vector Machine，LSSVM）的钟差预报组合模型[12]，获得了优于单一模型精度的预报结果，将钟差变化看作一个灰色系统，并建立了灰色预报模型，但该模型对稳定性较差的钟差序列预报精度不高。LSSVM为了降低模型复杂度，将标准向量机中的不等式约束化为等式约束，但LSSVM模型的预测精度依赖模型中核函数样式和模型固有参数的选择。目前，核函数形式和固有参数的选取较唯一，并不能保证选取最优[13]。

针对LSSVM在钟差预报中的缺陷，本文引入一种双核函数模型，采用常用径向基核函数和多项式核函数相加权的形式作为LSSVM模型的核函数，并提出利用改进粒子群算法（Improved Particle Swarm Optimization Algorithm，IPSO）优化加权值和模型参数。最后，设计时钟校准试验，采集校准过程中的钟差，并用实测钟差数据验证了上述预报方法的有效性。

1 时钟校准过程中的钟差预报技术

以目前常用的锁相环时钟校准模型为例[14-15]，其原理如图1所示。

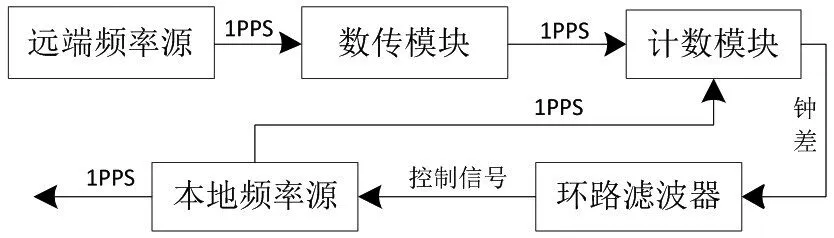
图1 时钟校准原理

计数模块测量并记录本地频率源的1 PPS时钟信号和接收到的1 PPS之间的钟差；环路滤波器根据钟差并结合一定的算法获得本地频率源的控制信号；通过控制信号对本地频率源进行控制，直至两个时钟信号达到同步。在同步站随机建站或建站距离较远的情况下，外界的1 PPS信号一般通过无线信道传输。当传输信道受到干扰和破坏时，时钟校准过程由于缺少参照1 PPS信号，从而不能正常进行。为保障时钟校准的顺利进行和时间同步的正常建立，在时钟校准模型中加入钟差预报模块，原理如图2所示。

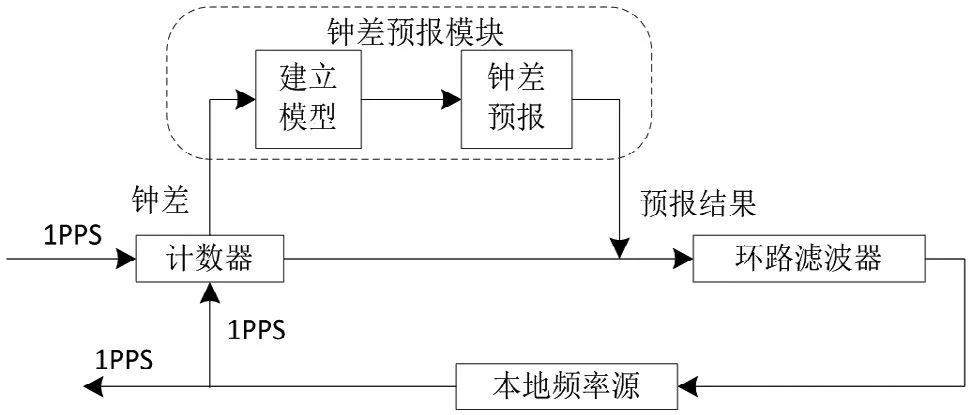
图2 时钟校准中钟差预报原理

钟差预报模块建模所需数据来源于计数模块测量和记录的钟差。钟差预报模块在外界时间信号传输失效时，结合已测的钟差和已建好的模型进行高精度钟差预报。环路滤波器根据预报后的钟差数据继续产生校准本地频率源所需的控制信号，从而保障时钟校准的正常进行。因此，在传输信道受到干扰和破坏时，钟差预报模型的预报精度直接影响着系统最终时间同步的效果。

2 高精度钟差预报模型

2.1 LSSVM模型

LSSVM模型的原理：T={xi, yi}1n为训练集，其中xi∈Rn为样本输入，yi∈R为样本输出。将输入数据在高维空间进行线性回归：F(x)=ωTφ(x)+b，φ是由低维到高维空间F的非线性映射，其中ω为权向量，b为偏差[12]。模型优化目标及约束条件分别为：

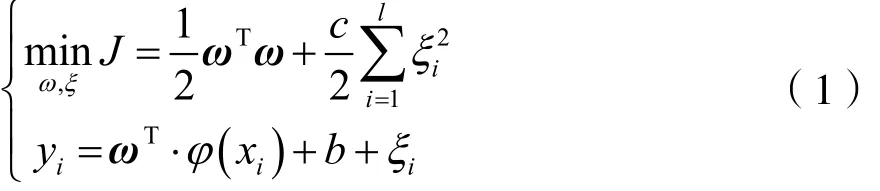
引入拉格朗日函数，并对式（1）中的ω、b、ξ、α求偏导，令偏导等于0，可解得：

式中，I=[1,1,…,1]T表示单位矩阵，C表示模型 的 惩 罚 因 子，α=[α1,α2,…,αn]T，Y=[y1,y2,…,yn]T，K=K(xk, xl)是满足Mercer条件的核函数。本文选取核函数类型为径向基函数和多项式函数的组合形式：

式中，σ表示核宽度参数，β表示权值。LSSVM预报模型如下：

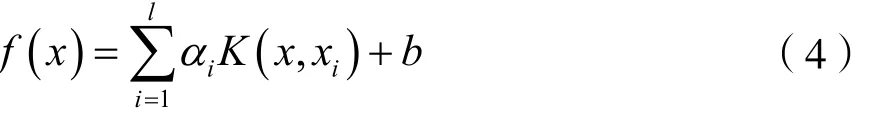
综上所述，此LSSVM模型的预测精度依赖于模型惩罚因子C、核函数参数σ以及权值β的选取[16]。PSO算法作为一种高效的寻优算法，在参数寻优等领域得到了广泛应用。下面介绍PSO算法的改进形式——IPSO的原理。

2.2 IPSO算法

IPSO算法是PSO的一种改进算法，改进之一是将初始化后的粒子群均分为两个相互独立的子群。其中，一个子群为主子群，迭代搜寻方式如下：

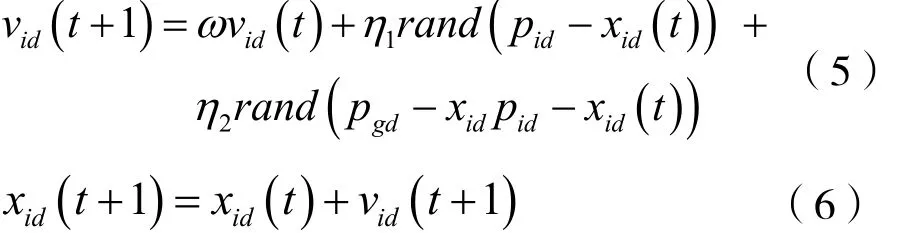
另一个子群为辅子群，搜寻方向与主子群相反：

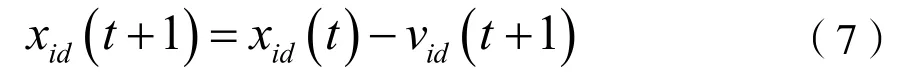
每次迭代完成后，比较主子群和辅子群的局部最优适应值，用局部适应值更优的子群粒子代替较差的粒子，并作为主辅子群共同的局部最优。同样，将全局适应值更优的粒子作为主辅子群共同的全局最优。

IPSO算法的关键因数是惯性权重ω。ω越高，越能提高IPSO的全局搜索能力；权重ω越小，越能增强IPSO的局部搜索能力[13]。为了权衡全局搜索能力和局部搜索能力，寻找最佳的惯性权重ω，改进之二是引入一种随优化代数而自适应调节惯性权重ω的方法：

式中，ωmax为最大权重，ωmin为最小权重，tmax为最大迭代次数，ti为当前迭代次数。早期的ω递减速度加快，能快速进入局部搜索，增强了局部搜索能力；后期的ω递减速度放缓，保证了全局搜索能力，提高了后期收敛精度。

2.3 IPSO优化LSSVM模型

利用IPSO算法对LSSVM中的惩罚因子C、核函数参数σ以及权值β优化的流程，如图3所示。

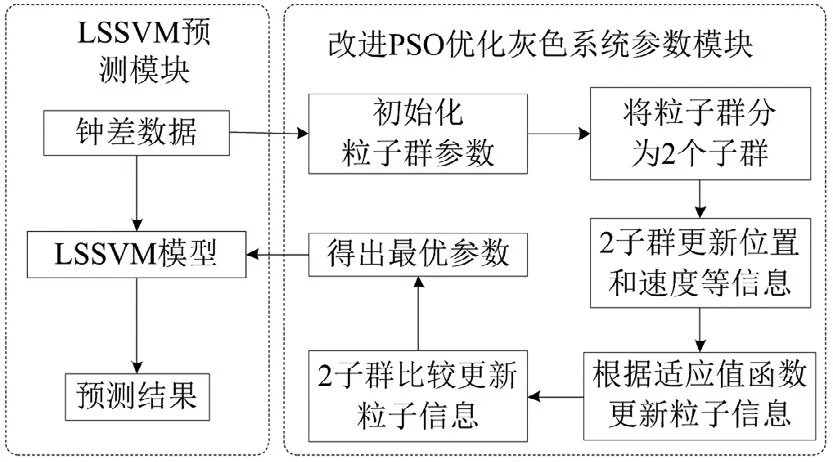
图3 改进模型的算法流程

IPSO优化LSSVM模型的具体算法步骤如下。

步骤1：模型参数初始化。初始化IPSO和LSSVM模型参数。

步骤2：参数寻优。按2.2节中论述方式更新惯性权重信息。

步骤3：确定最优值。构建适应值函数：

式中，xi是原始钟差数据，x^i是预测数据。两子群分别计算更新个体最优和全局最优，并将两子群中更优者作为两个子群共同的最优极值，进入下一步迭代。

步骤4：检查IPSO算法是否满足终止条件。若是，则求出最优解；否则，转向步骤3继续更新。迭代完成后，将最优参数组合注入LSSVM模型，获得最终的优化模型。

3 实例分析

为验证组合模型在时钟校准失效下钟差预报的精度，选取PSR10铷钟、Agilent53230A时间间隔计数器、Tektronix DPO3054示波器以及某型对流层散射传输设备等，设计时钟校准试验如图4所示。

图4 时钟校准试验

铷钟B产生1 PPS时钟信号，经对流层散射传输系统B通过衰减器直连进入对流层散射传输系统A，且衰减器模拟对流层散射信道的衰落特性。时间间隔计数器测量本地铷钟A和接收到的1 PPS时钟信号之间的钟差。PC机采集和记录钟差数据，并模拟锁相环原理产生同步铷钟A所需的控制信号。铷钟A根据控制信号进行调节，最终达到时间同步的目的。数据记录采样时间10 s。选取校准过程中某时段的240个钟差数据，其趋势项变化如图5所示。

图5 钟差数据

某时段的240个钟差数据呈下降趋势，说明随着时钟校准的进行，本地时钟信号和接收到的时钟信号之间的钟差越来越小，最终二者趋于同步。

将上述所测钟差数据分为建模集和检验集，分别用来建立模型和检验模型的精度。利用建模集分别建立二次多项式（QP）模型，LSSVM模型（核函数选取径向基函数，惩罚因子C和核函数参数用遍历寻优确定）和前文论述的IPSO-LSSVM模型，进而对后60个钟差数据进行预报。将平均误差ME（Mean Error）、均方误差RMSE（Root Mean Square Error）作为评价各模型优劣的指标，计算公式如下：

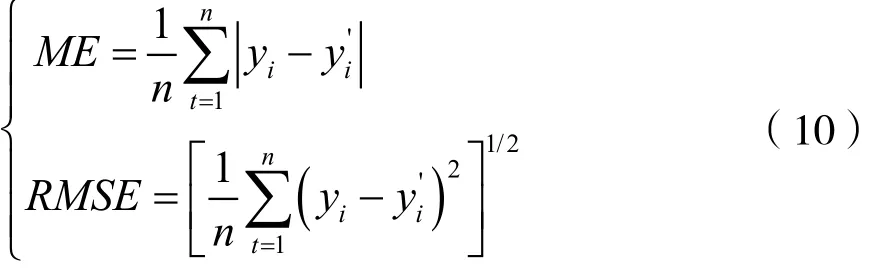
式中，yi和y'i分别表示实际测得数据和预报输出数据。不同模型的预报结果，统计如图6、表1所示。

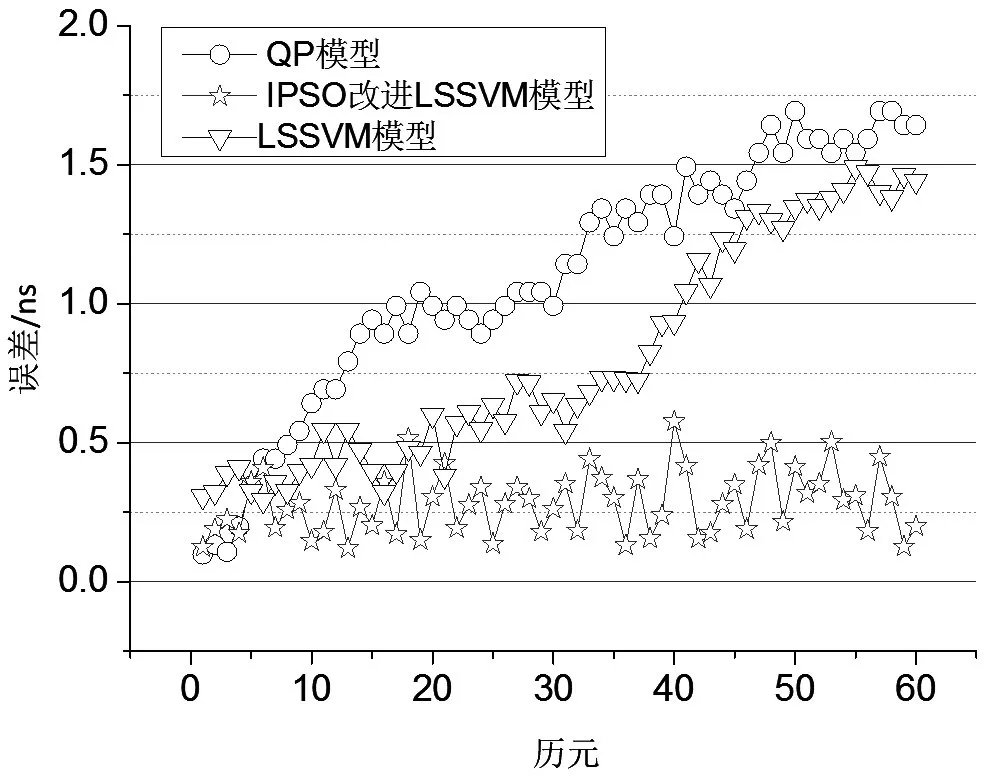
图6 误差数据统计结果

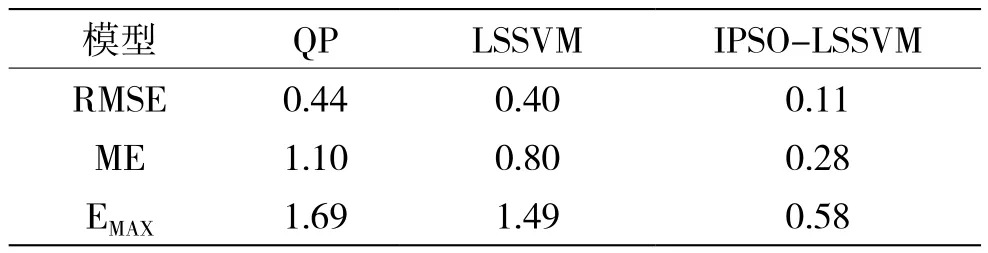
表1 三种模型的钟差预报统计值 /ns

分析图6、表1中60个钟差数据预报结果，可得出以下结论：

（1）改进后的LSSVM模型的均值ME和均方根误差RMSE均小于二次多项式和LSSVM模型，且具有较高的预报稳定性。

（2）改进LSSVM模型预报平均误差小于1 ns级别，因此在时钟校准系统出现故障的情况下，可利用其预报的钟差进行时钟校准，保障异常情况下的时钟校准精度。

（3）钟差预报模块与钟差校准模块并联在一起，预报模块并不影响正常情况下时钟校准的精度。

4 结 语

本文在时钟校准模型中引入钟差预报模块，以保障时钟校准系统异常情况下的时钟校准性能，并利用IPSO优化LSSVM模型中的参数和权值的选取。设计时钟校准试验，利用采集的钟差数据进行预报精度验证，结果表明，在10 min的预报时长中，误差约为0.28 ns。此外，该模型相对于传统二次多项式模型和LSSVM模型具有更高的预报稳定性，可用该组合模型的预报结果在异常情况下进行时钟校准。

[1] WANG Zheng-bo,ZHAO Lu,WANG Shi-guang,et al.COMPASS Time Synchronization and Dissemination Toward Centimetre Positioning Accuracy[J].Science China Physics,Mechanics and Astronomy,2014,57(09):1788-1804.

[2] 姜雷,郑玉平,艾淑云等.基于合并单元装置的高精度时间同步技术方案[J].电力系统自动化,2014,38(14):90-94.JIANG Lei,ZHENG Yu-ping,AI Shu-yun,et al.A Highly Accurate Time Synchronization Technology Scheme Based on Merging Unit[J].Automation of Electric Power Systems,2014,38(14):90-94.

[3] 向为,徐博,牟卫华等.基于锁相环的GNSS授时接收机钟差校准算法[J].国防科技大学学报,2013,35(02):115-119.XIANG Wei,XU Bo,MOU Wei-hua,et al.A Clock Error Calibration Algorithm Based on Phase Lock Loop in GNSS Time Synchronization Receiver[J].Journal of National University of Defense Technology,2013,35(02):115-119.

[4] 梁月吉,任超,杨秀发等.结合双树复小波和广义回归神经网络的钟差预报方法研究[J].测绘通报,2016(01):6-10.LIANG Yue-ji,REN Chao,YANG Xiu-fa,et al.Prediction of Satellite Clock Bias Based on Dual-tree Complex Wavelet Transform and GRNN[J].Bulletin of Surveying and Mapping,2016(01):6-10.

[5] 刘强,孙际哲,陈西宏等.对流层双向时间比对及其时延误差分析[J].测绘学报,2014,43(04):341-347.LIU Qiang,SUN Ji-zhe,CHEN Xi-hong,et al.Analysis of Two Way Troposphere Time Transfer and Its Delay Errors[J].Acta Geodaetica et Cartographica Sinica,2014,43(04):341-347.

[6] 崔先强,焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报:信息科学版,2005,30(05):447-450.CUI Xian-qiang, JIAO Wen-hai.Grey System Model for the Satellite Clock Error Predicting[J].Journal of Central South University(Science and Technology),2005,30(05):447-450.

[7] Xu B,Wang Y,Yang X.Navigation Satellite Clock Error Prediction Based on Functional Network[J].Neural Processing Letters,2013,38(02):305-320.

[8] Xu B,Wang Y,Yang X.A Hybrid Model for Navigation Satellite Clock Error Prediction[J].Computational Intelligen ce,2013,46(05):307-316.

[9] 季利鹏,徐波,高有涛.泛函网络在导航卫星钟差中长期预报中的应用[J].天文学报,2013,54(02):176-188.JI Li-peng,XU Bo,GAO You-tao.The Application of Functional Network in Medium and Long-term Prediction of Clock Error of Navigation Satellite[J].Acta Astronomica Sinica,2013,54(02):176-188.

[10] 席超,蔡成林,李思敏等.基于ARMA模型的导航卫星钟差长期预报[J].天文学报,2014,55(01):78-89.XI Chao,CAI Cheng-lin,LI Si-min,et al.Long-term Satellite Clock Bias Prediction Based on ARMA Model[J].Acta Astronomica Sinica,2014,55(01):78-89.

[11] 王国成,柳林涛,徐爱功等.径向基函数神经网络在GPS卫星钟差预报中的应用[J].测绘学报,2014,43(08):803-807.WANG Guo-cheng,LIU Lin-tao,XU Ai-gong,et al.The Application of Radial Basis Function Neural Network in the GPS Satellite Clock Bias Prediction[J].Acta Geodaetica et Cartographica Sinica,2014,43(08):803-807.

[12] 雷雨,赵丹宁,李变等.基于小波变换和最小二乘支持向量机的卫星钟差预报[J].武汉大学学报:信息科学版,2014,39(07):815-819.LEI Yu,ZHAO Dan-ning,LI Bian,et al.Prediction of Satellite Clock Bias Based on Wavelet Transform and Least Squares Support Vector Machines[J].Geomatics and Information Science of Wuhan University,2014,39(07):815-819.

[13] 刘赞,陈西宏,薛伦生等.改进粒子群优化最小二乘向量机卫星钟差预报[J].测绘科学,2015,40(09):115-118.LIU Zan,CHEN Xi-hong,XUE Lun-sheng,et al.Prediction of Satellite Clock Errors Based on GMLSSVM Improved by IPSO[J].Science of Surveying and Mapping,2015,40(09):115-118.

[14] 张晓蕊,许津铭,钱强等.变采样周期锁相环的分析与设计[J].电网技术,2014,38(09):2605-2610.ZHANG Xiao-rui,XU Jin-ming,QIAN Qiang,et al.Analysis and Design on Variable Sampling Period Phase-Locked Loops[J].Power System Technolo gy,2014,38(09):2605-2610.

[15] 陈西宏,吴文溢,刘赞.基于改进射线描迹法的对流层斜延迟估计[J].电子与信息学报,2016,38(10):2468-2474.CHEN Xi-hong,WU Wen-yi,LIU Zan.Estimation of Tropospheric Slant Delay Based on Improved Ray Tracing Method[J].Journal of Electronics & Information Technology,2016,38(10):2468-2474.

[16] 王新,孟玲玲.基于EEMD-LSSVM的超短期负荷预测[J].电力系统保护与控制,2015,43(01):61-66.WANG Xin,MENG Ling-ling.Ultra-short-term Load Forecasting based on EEMD-LSSVM[J].Power System Protection and Control,2015,43(01):61-66.