“三角形的三边关系”教学实录与评析
2018-03-12
教学实录:
一、出示结论,理解结论
师:在《几何原本》中有一句这样的话(课件出示图1)。来,齐读一遍。(板书:三角形任意两边之和大于第三边)能理解这句话的意思吗?谁愿意说一说?
生1:就是两边的长度和要比第三边长。
师:(在黑板上画出三角形)你能上来比划出你的意思吗?(生1比划)这就是任意两边之和大于第三边的意思吗?(底下有学生举手)你为什么举手?
生2:不止有这两边之和大于这一边,还有这两边之和大于这一边、这两边之和大于这一边。
师:你们都能听明白他说的意思吗?(有学生摇头)如果我给这三条边都取上名字,(给三角形的三条边分别标上a、b、c)你能再说一次吗?
生2:有a+b>c,还有a+c>b和b+c>a。(板书: a+b>c,a+c>b,b+c>a)
师:你们都同意吗?(生:同意)你现在明白这句话的意思了吗?(生1点头)你们都能明白?(其他学生点头)
二、验证结论
1.引出质疑,引发验证
师:这句话的意思你们是明白了,那对于这句话,你相信吗?(连续问一排学生)
学生有的说相信,有的说不相信。
师:有人相信,有人不相信,怎么办?面对一个结论,我们不能轻易相信,也不能轻易不信,怎么办?
生:验证。
2.学生验证,引发质疑
师:那你们要怎样验证?(生:画一个三角形)黑板上正好有一个三角形,用它试试可以吗?接下来干吗?
生:测量三条边的长度。(师测量并板书)
师:然后呢?(生:再比较)要比较几次?(生:3次)这个例子可以说明这句话是对的。那你现在相信这句话吗?(生:不相信)有例子可以说明这句话是正确的,为什么你还不相信?(生:还有其它的三角形)确实如此,只通过一个例子就能说明这个结论是对的吗?你们接下来想做什么?(生:再画一个三角形)请你们拿出铅笔、尺子在稿纸上举例验证。
学生动手画三角形,然后分组验证。
师:有谁愿意分享你的验证结果?分享时可以按照这样的形式:你画的三角形三条边的长度分别是多少,通过这个例子说明这句话是不是正确的。(请两个同学分享)通过刚刚的例子(板书:举例子)都说明这句话是对的。有没有说明这句话是错误的例子?(学生摇头)现在,你们相信这个结论了吗?(生:相信)有还不相信这句话的吗?(一生摇头)这么多人都相信了,你怎么还不相信?
生:不见得所有的三角形都是这样的,可能有特别的三角形。(有刚刚相信的学生又说不相信了)
师:你怎么变了?你怎么也变了?三角形的个数是无限的,我们能把所有的三角形都一一进行验证吗?(生:不行)那怎么办?
生:就像他说的,是不是有不是这样的三角形?
师:你怎么这么厉害呢?既然无法研究所有的三角形,我们有时候要换个角度思考:是不是有两边之和不大于第三边也能围成三角形的?(板书:不大于)如果有一个这样的反例存在,(板书:反例)我们就可以说这个结论是错的。
3.寻找反例,引发矛盾,深度感受
师:下面我提供一些数据,要研究反例的话,你怎么选?(出示图2)(生:4、5、10)为什么?(生:因为4+5<10)(板书4、5、10)还有其他的选择吗?(生:4、6、10)为什么?(生:因为4+6=10)(板书:4、6、10)
师:这样吧,下面我们先研究三条边长分别为4厘米、6厘米、10厘米能否围成三角形。请你们打开学具袋,用三根这样长度的纸条围一围,看能不能围成三角形。(学生动手围)有能围成三角形的吗?请你上台围一围。(学生上台展示)你们觉得这个是边长分别为4厘米、6厘米和10厘米的三角形吗?
生:不是,这两条边的顶点没连接在一起。
师:有人认为这是(4、6、10)的三角形,有人不同意,怎么办?当我们用实物操作遇到问题的时候,我们可以借助想象来解决。(出示图3)如果要围成三角形,该怎么办?(生:把4、6两条边往中间靠)(课件演示从图3到图4的过程,学生感受两边的运动过程及运动轨迹)
师:(指上台围三角形的学生)你现在还觉得(4、6、10)能围成三角形吗?(生:不能)为什么你变了?
生:因为当4厘米和6厘米连在一起时会与10厘米的线段重合。
师:还有觉得(4、6、10)能围成三角形的吗?(有个别学生脸上有疑惑但是没举手)我们再来感受一次(课件演示图3-图4的过程)我知道,你们一定会有疑问,通过想象(4、6、10)不能围成三角形,為什么用实物又好像能围成呢?(出示图5)这几根是长度分别为4厘米、6厘米、10厘米的三条线段。要把它们围成三角形,我们得这样。(课件演示由图5到图6的过程)围成三角形后,我们可以找出它们的三个顶点。不难发现,我们围成的三角形其实并不是实物表示的那样,而应该是用虚线表示的三角形。这个三角形的上面两条边的长度分别为多少?(生:4厘米、6厘米)那底下的那条边长度是多少?(生:不知道)有10厘米吗?(生:没有)如果底边长有10厘米会怎么样?(生:会与上面两条边重合)现在能明白,实物围成的三角形的边长并不是(4、6、10)了吧!那(4、5、10)你们觉得可以围成三角形吗?(生:不可能)endprint
师:你是怎么想的?
生:(4,6,10)都不可能围成三角形,(4,5,10)就更不可能围成三角形了。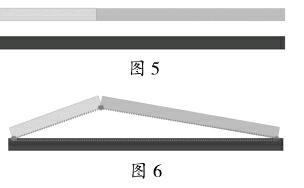
师:为什么更不可能?
生:因为4厘米和5厘米加起来还没有10厘米长,围不成。
师:你们都是这样想的吗?我们一起来看看。(课件演示图7)通过刚才的观察,你们觉得两边之和等于第三边可以围成三角形吗?(生:不能)那两边之和小于第三边能围成三角形吗?(生:不能)也就是说我们找不到反例。
师:现在你们相信这句话吗?(生:相信)同学们,面对一个结论,如果我们能找到一些例子说明它是正确的,又不能找到反例,我们就可以相信它。今天我们学习的内容就是三角形的三边关系。(板书课题)我希望今天你们能学会这个内容,更希望你们能记住今天我们学习内容的这个过程,期待以后的你们越来越会学习数学。今天我们的课就到这了,谢谢你们,下课!
评析
“三角形任意两边之和大于第三边”是平面几何中有关三角形三边关系的一条重要定理,位于《几何原本》第20号命题。在《几何原本》中,它是利用“大边对大角”的定理证明的。人教版初中数学教材中是通过观察简单的几何事实,结合“两点之间线段最短”这一朴素、直观的公理推导出三角形的三边关系。
在小学数学课堂,三角形的三边关系的教学路径一般是这样的:首先,抛出问题“什么样的三条线段才能围成三角形”。接着,发给学生一些长度不等的纸条,比如,长度分别为4cm、5cm、6cm、10cm的四根纸条,让学生动手操作,试图获得一些事实:(4cm、5cm、6cm)与(5cm、6cm、10cm)可以围成三角形,而(4cm、6cm、10cm)与(4cm、5cm、10cm)却不能围成。最后,引导学生归纳总结出:三条线段满足任意两条线段长度的和大于第三条线段时可以围成三角形(为叙述方便,我们称之为结论①,以下同),即三角形任意两边之和大于第三边(结论②)。
严格地说,结论①是判定,是对教师教学伊始所抛出问题“什么样的三条线段才能围成三角形”的回答,而结论②是性质,它回答的问题是三角形三边具有什么样的关系。两者互为逆命题,逻辑上并不等价。但在实际教学中,老师们就是这么做的:为了得到结论②,先研究结论①。这样倒过来研究,在教学中将面临以下两个问题。
第一个问题,当回答“什么样的三条线段能围成三角形”时,学生归纳出的结论常常是两条较短线段的和大于第三条线段时,能围成三角形(结论③)。这一结论对于判断三条线段能否围成三角形来说,比结论①三条线段满足任意两条线段长度的和大于第三条线段时,可以围成三角形更简洁有力,因为结论③只需判断一次,而结论①却需要判断三次。但结论③并不是本节内容想要达成的教学目标。第二个问题,我们知道,当两条线段等于第三条线段时,比如(4cm、6cm、10cm),是不可能围成三角形的,但学生动手操作时,由于实际操作中存在误差,却常常“围成”了三角形,而且对此坚信不疑。这是三角形的三边关系教学中公认的教学难点。
我们知道,教学三角形的内角和时,一般是先给出一些形状、大小各异的三角形,再要学生通过测量和计算各个三角形的内角和,探索三角形内角和有什么规律。学生通过测量和计算很容易发现三角形的内角和等于(或接近)180度,从而较顺利地归纳出结论“三角形的内角和是180度”。受此启发,教学三角形的三边关系时,我们能不能也顺过来,从正面直接研究三角形三边的长度有什么规律(性质)呢?答案是否定的。比如,给出一些三角形(如下图所示),接着学生测量出每条边的长度,然后提出问题:“仔细观察,你有什么发现?”学生是不可能通过观察三角形各边的长度发现三角形两边之和大于第三边这一结论的。不止学生不能,一般成年人如果之前不知道这个结论,也很难做到。这也是小学数学课堂教学三角形的三边关系时倒过来研究的一个重要原因。
怎么办呢?周楷老师给出了一条解决该问题的思路。
周楷老师的三角形的三边关系的教学路径显然不同,没有采取所谓的探究性学习,而是将教学重心放在如何理解这个结论上。虽然直接给出结论,但没有降低教学的难度和思维的含量,相反整节课的数学味更浓,思维含量更高,是一种有意义的接受性学习。
首先,直接把結论“三角形任意两边之和大于第三边”抛给学生,提出问题:“你明白这句话是什么意思吗?”在学生理解这句话后,接着追问:“你相信吗?”“信或者不信,应该怎么办?”引发学生产生用事实验证的冲动,“画一个三角形看看”。画出三角形后,“怎么验证呢?”引导学生测量三条边的长度。
整节课,可以分为“理解、质疑、验证、思辨”四个环节。对于学生来说,每一个环节都是一次思维上的考验。事实上,仅仅理解这个结论就不是一件容易的事。“任意是什么意思?”“对于一个具体的三角形而言,任意两边之和大于第三边,意味着什么?”这些问题对一个四年级的学生来说都不容易回答。只有当学生明白“对于一个具体的三角形而言,当三条边a、b、c同时满足a+b>c、b+c>a、a+c>b时,才能说任意两边之和大于第三边”这个道理后,才算真正理解了这句话。
如何验证是学生经历的又一次考验。画一个三角形,要验证任意两边之和大于第三边是否正确,我们该怎么做呢?学生其实并没有这方面的经验。验证完黑板上的三角形后,学生又各自画出一些三角形,通过测量验证结论的正确性。问题是,这样就够了吗?从正面举例子,例子再多,也不能说明结论是正确的。怎么办?找反例!如果能找到一个反例则说明结论是错误的,如果找不到反例,则结论就更可靠。以上关于验证的整个过程对于学生来说,由于平时缺乏相关训练,因此更显得弥足珍贵。
最后一个思辨环节将整节课推向高潮。学生动手操作时,似乎(4、6、10)也能围成三角形。但在动画演示的帮助下,通过想象及理性的思考,学生最终明白(4、6、10)是不可能围成三角形的。
以上是周楷老师本节课的价值所在。对于教材中众多不太好进行探究性学习的教学内容而言,本节课提供了一条全新的思路。这种处理方式值得推广。
(作者单位:长沙市岳麓区博才寄宿小学长沙市岳麓区教研室)endprint
