考虑多能耦合及品位差异的含储能微网可靠性评估

葛少云, 李吉峰, 刘 洪, 王 莹, 孙 昊, 路志英

(1. 智能电网教育部重点实验室(天津大学), 天津市 300072; 2. 国网天津市电力公司, 天津市 300010)

0 引言

随着能源互联网建设的不断深入,打破各供能系统单独规划、独立运行的既有模式,实现电、气、热(冷)多能源的协同供应,将是未来供能系统的发展趋势。而作为能源互联网的关键节点,综合能源微网由于其灵活的运行方式,受到了广泛的关注[1]。供电可靠性是衡量电力系统持续供电能力的重要指标,是提出理想规划方案的基础。对于多能耦合的综合能源系统,可靠性评估同样重要,而多能源系统之间耦合特性的增强也对可靠性产生了一定的影响:一方面,由于能源之间的耦合关系,对于需求侧而言相当于拥有多个能源供给点,增强了供能可靠性;另一方面,由于供能系统的多能耦合,某个供能系统出现问题都可能对系统整体的能源供给产生影响。因此,研究面向多能耦合的可靠性评估方法是目前亟待解决的重要问题。

针对综合能源微网概念与架构的建设,文献[2]率先提出了能源集线器模型;在此基础上,文献[3]进一步提出了综合能源系统的概念。同时,随着微电网概念[4-6]的提出,分布式供能及储能装置进一步融入综合能源系统,形成运行方式更加灵活的综合能源微网,为可再生能源的有效消纳及与能源主网的相互支撑提供保障。

作为运行及规划过程中的关键技术,可靠性评估方法的研究一直得到广泛的关注。在元件停运分析环节,解析法与模拟法[7-8]是电力系统常用的方法;在系统状态评估环节,故障模式影响分析(FMEA)法通过遍历元件故障对系统负荷的影响,被广泛使用,其计算思路也被应用到微电网可靠性[9-10]的评估中。然而,针对综合能源供能可靠性,目前的研究较少。对于主动配电网,文献[11]分析了包含分布式电源与电动汽车的能源集线器的运行模式,并建立可靠性评估的数学解析模型;文献[12]建立双层网络分区模型,并结合蒙特卡洛模拟法评估可靠性。针对多能源网络,文献[13-14]以能源集线器作为研究对象,建立能源传输的状态空间,通过数学解析模型实现多能源系统的可靠性评估;文献[15]通过建立电网与燃气网中元件设备的状态模型,结合蒙特卡洛模拟法建立可靠性评估模型,并评估系统典型时段的可靠性。

上述成果为本文课题的研究奠定了一定的基础。然而,现有的研究存在以下问题:①研究对象大多仍停留在以电能为代表的单一能源网络,难以满足综合能源协同规划的需求;②常规数学解析方法无法体现机组设备及用户需求时序方面的特征;③上述文献缺少对储能能量充放策略影响的考虑;④上述文献未能考虑不同能源之间的能源品位差异化并由此产生的供能优先级和负荷削减的策略。

针对传统可靠性评估方法只能评估单一能源网络可靠性的问题,本文首先结合能源集线器模型分析多能源网络的耦合关系。其次,通过FMEA法与蒙特卡洛模拟法相结合的方式,在分析微网系统内部能量关系的基础上,进一步体现微网系统运行的时序特性,弥补数学解析法的不足。然后,对储电、储热装置在微网系统不同运行模式下的充放策略进行分析,以体现各类储能装置对能量平衡产生的影响,在此基础上,通过微网系统的运行模式、负荷削减策略与评价指标三个方面,体现不同能源之间的能源品位差异。最后,通过算例对比分析,说明本文所提方法的有效性与实用性。

1 综合能源微网架构

综合能源微网是可以自治运行的能量系统,由能量管理设备、分布式可再生能源装置、储能装置、能量转换装置和能源负荷组成,在结构上可分为能源输入、转换、存储和输出等环节。本文结合能源集线器模型,构建包含分布式冷热电联供机组、燃气热泵、分布式光伏系统、电制冷机、储电装置、储热装置等设备,及电、气、热(冷)多种终端能源在内的综合能源微网,典型的微网系统的结构如图1所示。

图1 综合能源微网结构图Fig.1 Structure of multi-energy microgrid

综合能源微网作为能源互联网在用户终端、独立可控的基本单元,其灵活的运行模式可以降低能源在传输过程中的损耗,同时实现可再生能源的有效消纳。后文将主要针对微网系统两种典型运行模式的可靠性进行分析,即并网式与电孤岛式运行模式。同时,本文对综合能源微网模型做出如下假设。

1)针对综合能源微网内部的网架结构,能源配送网均为单母线辐射网结构,并考虑设备之间的隔离。

2)不同类型的能源负荷由相应的机组集中供给。

3)不同机组设备的故障相互独立,并且只考虑单重故障的情况[16]。

4)假设外部能源主网络能在必要时刻提供足够的电能和天然气。

2 综合能源微网可靠性评估

2.1 设备元件状态模型

在微网系统内,以光伏与冷热电三联供为代表的机组设备出力及不同能源负荷的需求均具有较强的时序特性,仅通过数学解析的方法难以反映微网系统内的时序特性,从而影响可靠性的评估结果。因此需要建立设备元件的状态模型,并结合蒙特卡洛法模拟设备机组状态,体现微网系统内时序特性。

对于微网系统内机组设备的处理方法采用马尔可夫两个状态模型来进行描述[17]。即机组设备的正常状态采用指数分布,机组设备从正常状态运行到故障状态的持续时间为:

(1)

式中:λk为第k类元件设备的故障率;n为机组设备的总数;uk为[0,1]区间均匀分布的随机数。

机组设备均为可修复设备,故障持续时间同样采用指数分布,机组设备的故障持续时间为:

(2)

式中:μk为第k类元件设备的修复率。

2.2 可靠性评估指标

本文分别选取能量供给期望、缺供能量期望、能量不足持续时间作为评估综合能源微网不同类型能源可靠性的指标,并在此基础上结合能源价格构建综合能源可靠性评价指标。指标的意义与计算方法如下。

1)能量供给期望(RESS)

该指标表示在统计时间段内某一类型能源能够顺利传输到用户需求侧的概率,能源供给期望越高,代表该类型能源在抽样时间段内能源供给能够满足能源需求,供能可靠性越高。具体求解方法如下。

将能源集线器模型中的能源转换矩阵[2]扩展为能源传输功率矩阵C,C矩阵包括机组供应矩阵Cm和可调用资源矩阵Cs,矩阵的表达形式如式(3)和式(4)所示。矩阵的行代表运行过程中可能出现的不同运行场景(包括正常运行及故障场景);矩阵的列代表针对电能、热能、冷能的供应。

Cm=

(3)

(4)

式中:Cm为某一时间段内机组按照不同类型能源需求所提供的出力;Cs为某一时间段内后备资源或者外部电网可以为微网提供的能量,具体数值大小与制定的运行策略有关;CCCHP为热电冷联产系统的出力;CPV为光伏的出力;CGHP为燃气热泵的出力;CCAC为电制冷机的出力;CEN为外部电网可以提供的电量;CES储电装置可以提供的电量;CHS为储热装置可以提供的热量。

因此,在抽样时间段内对应第i种场景的能源传输矩阵Ci=Cm,i+Cs,i。同时,建立负荷能源需求矩阵L=[Le,Lh,Lc],表示在抽样时间段内电、热、冷能源的需求情况,下标e, h, c分别代表电能、热能和冷能。

在此基础上,建立供给/需求对比矩阵Q,Q矩阵内的元素是布尔变量,矩阵中的元素Qk,j,i表示第k(k∈{e,h,c})种能源,在第i(i∈{1,2,3,4,5})种场景下的第j(j∈{1,2,…,N})次抽样的判别情况。以电能为例,矩阵中的判别方法为:

(5)

因此,微网系统内电、热、冷能这3种能源的能源供给期望的计算方法如下:

(6)

(7)

(8)

式中:N为蒙特卡洛模拟抽样的时间段数。

2)缺供能量期望(RLOEE)

该指标表示在统计时间段内,某一类型能源由于机组故障或停运事故所缺供的总能量。缺供能量期望越高,代表该类型能源受机组故障的影响越大,供能可靠性越低。缺供能量期望的求解方法为:

(9)

(10)

(11)

式中:T为蒙特卡洛模拟的时长。

3)系统能源不足持续时间(RSAIDI)

该指标表示在统计时间段内,某一类型能源由于机组故障或停运事故所造成能源供给不足的持续时间。时间越长,代表该类型能源受机组故障的影响越大供能可靠性越低。具体求解方法为:

(12)

(13)

(14)

4)综合能源可靠性影响评价指标

本文基于文献[18]的分析思想,通过不同类型能源缺供能量期望结合相应能源价格,计算综合可靠性影响评价指标。指标数值从价格方面评估机组设备失效对微网系统造成的损失。具体测算如式(15)所示:

I=weRLOEE,e+whRLOEE,h+wcRLOEE,c

(15)

式中:I为综合可靠性影响评价指标,表示停运造成能源不足的损失,数值越大代表机组失效对微网系统供能可靠性的影响越严重;we,wh,wc分别为电、热、冷能的能源价格。

2.3 机组设备运行机制及元件时序模型

2.3.1运行机制分析

1)机组运行机制

综合能源微网内包含多种设备机组,通过互补来满足不同能源负荷的需求。电负荷由冷热电三联供机组及光伏系统进行供应,若出力不足则考虑调用储电装置或者从外部电网购电;热负荷由冷热电三联供机组及燃气热泵进行供应,若出力不足,则考虑调用储热装置;冷负荷由冷热电三联供机组及电制冷机进行供应。不同形式的能源优先考虑同类能源负荷的供给及储能装置的补充,如有剩余,再考虑参与能源转换与支援,以体现不同能源品位的差异。

作为微网系统内的关键设备,燃气冷热电三联供机组将为吸收式冷机、换热器等自身设备及微网系统内的电、热、冷负荷供电。机组的运行方式为以热(冷)定电,动力设备根据微网内所需的热(冷)量运行。发电量与微网实际电负荷存在偏差,当发电量高于所需电量时,多余电量输送至储能装置或者上网卖出;发电量不足时,从电网购电或由微网内其他资源(例如光伏系统、储电装置)进行补充。综合能源微网内冷、热负荷存在差异,当差异较大时,为保证燃气三联供机组的效率,燃气机三联供组的出力按照热负荷和冷负荷中较小的值进行配置[19]。

2)储能运行机制

微网系统包含储电与储热两种形式的储能装置。其中,储电装置作为微网中的可调控资源,能够提高能源利用效率及供能可靠性。在并网运行模式下,结合实际情况,储电装置在任意时刻的充放电状态与相关机组的出力及电价机制有关。同时,考虑到不同能源的品位问题,电能在过剩情况下会优先对储电装置进行供给,如再有剩余,再考虑能源转换问题。参考文献[20]所介绍的储能运行方式,多能源微网系统内储电装置的运行机制如图2所示。

图2 并网模式下储电装置运行机制流程图Fig.2 Flow chart of operation mechanism of energy storage devices under grid-connected mode

在电孤岛运行模式下,储电装置主要发挥可调用后备资源的作用,具体的运行机制如图3所示。

图3 电孤岛模式下储电装置运行机制流程图Fig.3 Flow chart of operation mechanism of energy storage devices under electric-isolated mode

对于储热装置,由于微网系统采取“以热(冷)定电”的运行机制,在正常运行状况下不会生产多余的热量。因此,本文所构建的综合能源微网采用以蓄热式电锅炉为代表的电储热装置,通过将多余的电能转换成热能,实现对热能的储存,从而起到后备可调控资源的作用,同时体现不同能源品位的差异性。

另外,本文在涉及运行与时序方面的分析中,考虑了机组/储能设备的出力约束、储能设备的容量约束、机组出力的爬坡约束、微网系统与外部电网的功率倒送约束等反映实际运行情况的约束条件。由于篇幅限制,本文不逐一列举说明。

2.3.2元件时序模型

1)电负荷模型

本文采用文献[21]中的电负荷模型,该模型通过负荷的典型年—周曲线、周—日曲线和日—小时曲线形成实时的负荷数据,既计算简便,又能很好反映负荷的时变特性。具体的数学表达式为:

Lt=LpPwPdPh(t)

(16)

式中:Lp为年负荷峰值;Pw为与第t个小时对应的年—周负荷曲线中的值;Pd为与第t个小时对应的周—日负荷曲线中的值;Ph(t)为与第t个小时对应的日—小时负荷曲线中的值。

2)光伏出力模型

光伏阵列的实时输出功率主要与实时的光照强度和温度有关。但是,考虑到温度的影响比较小,而且一般情况下光伏阵列均配备了最大功率跟踪装置,故可以认为光伏系统的实时出力主要取决于光照强度。因此,本文采用文献[22]中的光伏模型,以反映光伏出力的时序特性。数学表达式为:

(17)

式中:Pb为光伏的实时出力;Psn为光伏的额定功率,表示在标准测试条件下单位光强所能产生的功率;Gstd为额定光照强度;Rc为某一特定强度的光强,在该光强下光伏出力与光强的关系开始由非线性变为线性;Gb,t为第t个小时的实时光强,Gb,t的实时序列可以通过对历史光强的概率分布统计的抽样得到,也可以利用文献[23]中介绍的HDKR模型产生。

2.4 基于能源集线器模型的FMEA与负荷削减

本文通过FMEA法,分析微网系统内能源供给的逻辑关系,量化分析机组故障对不同类型能源供给可能产生的影响,同时体现不同能源之间的耦合特性。以并网式运行的综合能源微网为例,微网系统内电、热、冷不同类型能源的可靠性状态为:

(18)

式中:Re,Rh,Rc分别为电、热、冷能供给的可靠程度;f(·)表示能源供给可靠性的等级函数;SCCHP为冷热电联供机组的状态(正常或故障状态);SPV为光伏机组的状态;SES为储电装置的状态;SEN为外部电网的状态;SGN为外部燃气网的状态;SGHP为燃气热泵的状态;SHS为储热装置的状态;SCAC为电制冷机的状态。

针对图1所示的综合能源微网结构,本文考虑并分析了燃气冷热电三联供、燃气热泵、电制冷机、光伏机组、储电装置等设备装置故障及外部电网、燃气网故障造成供给中断对微网系统的影响。由于篇幅的限制,本文重点对燃气冷热电三联供在故障后的影响进行说明,分析量化不同能源之间的耦合关系。另外,在本文下述研究内容中,将一年分为8 760个时段,即每个时段为1 h,在每个时段中,假定设备状态参数保持不变,对于瞬时量采用某个时段中的某个时刻的量来描述。

在燃气冷热电三联供发生故障后,会影响冷、热、电三种能源的供应。其中,电负荷主要由光伏系统进行供给,储电装置及上级电网进行后备补充;冷负荷在电能有剩余并且满足电制冷机出力约束的情况下由电制冷机进行供给;热负荷在满足燃气热泵出力约束的情况下由主要由燃气热泵进行供给,储热作为后备补充。在故障发生后,微网系统会按照重要程度保障电、热、冷重要负荷的供给,而对于同等重要程度的负荷会依据能源品位的差异,制定负荷供给的优先级。

结合2.2节介绍的评估指标,缺供能源期望可以由式(19)和式(20)计算得到。

(19)

RLOEE,e,ke,CCHP=

(20)

式中:RLOEE,CCHP,e为冷热电三联供故障造成电能的缺供能源期望;RLOEE,e,ke,CCHP为受冷热电三联供故障影响所造成相应区域内的缺供电量期望;λCCHP为冷热电三联供机组的故障率;r1和r2分别为故障的起止时刻,时间跨度为冷热电三联供机组的修复时间rCCHP;Le(τ)为τ时刻电力负荷的需求;CES(τ)为τ时刻储电装置可提供的电量;CPV(τ)为τ时刻光伏出力;CEN(τ)为τ时刻外部电网可提供的电量。

系统能源不足持续时间为:

(21)

(22)

式中:RSAIDI,CCHP,e为冷热电三联供故障造成电能的能源不足持续时间;RSAIDI,e,ke,CCHP为变冷热电三联供故障影响所造成相应区域内电能的能源不足持续时间。

同理,通过式(23)至式(26)的计算可以得到热能与冷能相应的可靠性指标。

RLOEE,h,kh,CCHP=

(23)

RLOEE,c,kc,CCHP=

(24)

(25)

PSAIDI,c,kc,CCHP=

(26)

式中:RLOEE,h,kh,CCHP和RLOEE,c,kc,CCHP分别为冷热电三联供故障造成热能与冷能的缺供能源期望;Lh(τ)和Lc(τ)分别为τ时刻热负荷与冷负荷的需求;CGHP(τ)为τ时刻燃气热泵的出力;CHS(τ)为τ时刻储热装置可以提供的热量;CCAC(τ)为τ时刻电制冷机的出力;RSAIDI,h,kh,CCHP和RSAIDI,c,kc,CCHP分别为冷热电三联供故障造成热能与冷能的能源不足持续时间。

通过式(24)和式(26)对冷能源的分析,由于在正常运行状态下一部分冷负荷由电制冷机进行供给,因此,在故障发生后,对于同等重要程度的能源负荷而言,考虑到电能的能源品位高于冷能及两种能源需求的刚性/柔性特征,系统将会优先供给电负荷,而由电制冷机供给的冷负荷在故障后可能会被削减以保障对电负荷的持续供应。

同理可分析其他机组故障对综合能源微网不同能源供给产生的影响。另外,本文对电孤岛运行模式的FMEA分析将不考虑外部电网故障对微网系统的影响,同时在分析过程中不考虑外部电网的供给CEN。

3 综合能源微网可靠性评估流程

面向综合能源微网的供能可靠性评估主要包括参数收集与数据生成、蒙特卡洛模拟、故障影响分析及可靠性指标统计计算4个主要部分。具体的评估流程图如图4所示。

图4 综合能源微网可靠性评估流程图Fig.4 Flow chart of reliability evaluation of multi-energy microgrid

4 算例分析与对比

4.1 算例概况

本文以中国南方典型工业园区为例,物理结构与设备构成如图1所示。能源供给与需求方面,4月至10月为供冷期,体现为冷负荷需求较大;热负荷主要包括生产过程中存在的烘干、新风及生活中的热水等需求,虽然没有明确的供应期,但也具有一定的季节特性;全年均有电负荷需求,微网系统内全年的电、热、冷负荷需求特性曲线如图5所示。机组的运行参数见附录A表A1,其中,储电装置的初始容量选取额定容量的30%,最大充放电功率选取额定容量的7.5%[24]。储热装置的初始容量选取额定容量的50%,最大充放热功率选取额定容量的80%[25]。综合考虑可用面积、发电效率等因素,光伏机组的装机容量为4.6 MW,年出力特性曲线如图6所示,微网系统向上级主电网的倒送功率上限为200 kW[26]。结合当地实际的阶梯电价政策方案,11:00—15:00和19:00—21:00为峰值电价；0:00—7:00为谷值电价；剩余时段为平值电价[27]。各类设备机组的可靠性参数见附录A表A2,其中,上级主电网选取的是电源侧主变压器/母线的故障率及修复时间;上级燃气网选取的是主要输气管道的故障率及修复时间。

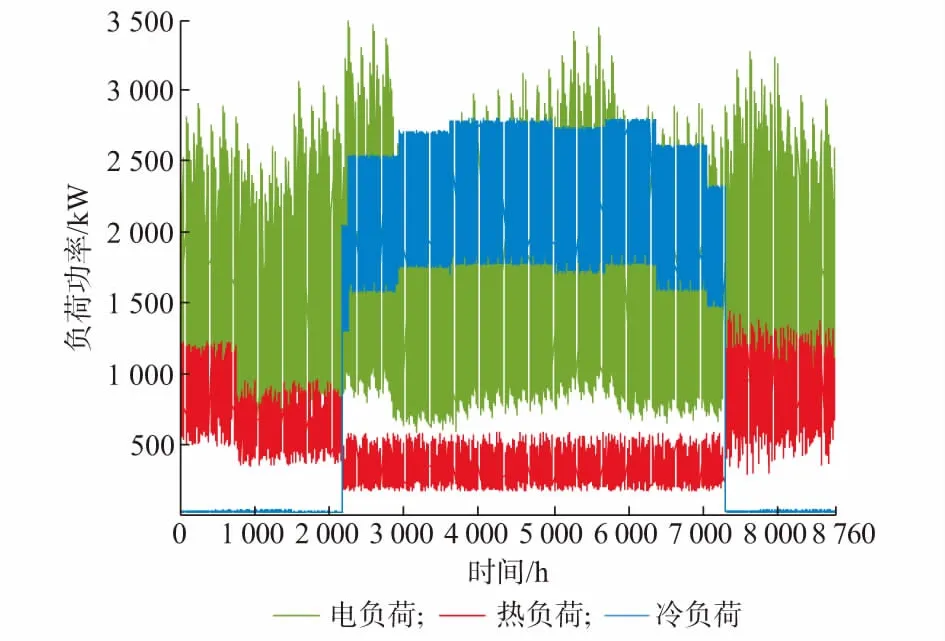
图5 负荷需求曲线Fig.5 Load demand curve

图6 光伏出力曲线Fig.6 PV output curve

4.2 全年可靠性指标分析

本文将蒙特卡洛模拟时长设定为10 000 a,即T=10 000。通过蒙特卡洛模拟结合FMEA法,分别计算综合能源微网在并网及电孤岛两种运行模式下的年可靠性指标如表1所示。

表1 不同运行模式年可靠性指标对比Table 1 Comparison of annual reliability indices under different operation modes

对比不同运行模式下综合能源微网年可靠性指标,相比较于并网运行模式,电孤岛运行模式由于没有外部上级电网作为后备支撑,因此,电网侧的可靠性有所下降。同时,由于能源供给策略方面考虑了能源品位的因素,因此在电能供给不足时会切断通过电制冷机对与冷能源的供给及切断通过电锅炉对热能源的储存,以保障电能的有效持续供给,反映到热能源与冷能源的供给会受到不同程度的影响。其中,电制冷机在供给过程中会直接受到电能的影响,造成冷能源的供能可靠性相比于热能源下降较大;而电储热装置在本文所构建的微网系统内主要起到后备资源的作用,因此,热能源的供能可靠性下降较小。

4.3 预安排停运分析

在评估综合能源微网年可靠性指标的基础上,本文进一步选取典型时刻,通过模拟冷热电三联供机组的预想故障,从而构造对电、热、冷三种能源均会产生影响的典型场景,进一步说明在不同能源需求情况下,多能源耦合对供能可靠性的影响。

本文分别选取电负荷、热负荷、冷负荷在一年内的峰谷时段,模拟冷热电三联供机组的停运失效,评估综合能源微网在不同能源需求及不同运行模式下的缺供能量期望及停电时间期望(Er),同时为保证预想故障造成的影响时间相同,预安排停运时长选取为故障修复时间的参考值,即24 h。评估结果如表2和表3所示。

表2 并网运行模式典型时段可靠性指标Table 2 Reliability indices during typical time period under grid-connected mode

表3 电孤岛运行模式典型时段可靠性指标Table 3 Reliability indices during typical time period under electric-isolated mode

通常情况下,在对单一能源网络进行预安排停运检修时,通常会避开负荷峰值以确保造成的影响最低。然而,以电孤岛运行模式为例,通过对比同一种运行模式在不同典型时段的可靠性指标可以得到,在某一种能源负荷的谷值进行预安排停运虽然能在一定程度上保证该能源的可靠供应,但是在综合考虑多能源耦合及供能周期的情况下，却可能对其他能源产生较大的影响。例如在电负荷的谷值模拟故障,对冷负荷造成的影响甚至会超过在电负荷的峰值模拟故障。而对比不同运行模式在不同典型时段的可靠性指标可以得到,相比较于并网运行模式,电孤岛运行模式由于缺少了重要的后备资源,电能的供应受到了影响;同时由于能源之间的耦合关系,也对冷能的供应及热能的存储间接产生了影响。

在此基础上,进一步分析综合可靠性影响指标,并依此分析最优检修时段。以中国南方地区为例,不同类型的能源供给价格见附录A表A3。

通过计算,在并网运行模式下,在时刻t=2 120进行预想事故模拟,得到Imin=0,在该时刻开始模拟冷热电三联供机组的停运失效,受影响的负荷可以借助外部电网及其他机组进行转带,不会对微网系统的能源供给产生影响;在电孤岛运行模式下,在时刻t=3 500进行预想事故模拟,得到Imin=13 326.314 元,由于光伏机组在模拟时段内出力较高,配合储电装置能够有效减少缺供电量,多余的电量也可以通过电制冷机对冷负荷进行供给,而热负荷可以由燃气热泵完全转带,因此,相较于其他时刻对微网系统可靠性造成的影响较小。

5 结语

在能源交互频繁和通信手段多样化的背景下,多能源子系统通过相互关联耦合构成的综合能源微网是能源互联网中的重要组成部分。如何改善常规的能源利用形式,推动能源之间的协调发展是今后研究的重中之重。本文以综合能源微网作为研究对象,提出了一种可靠性评估方法。在评估的过程中,充分考虑了供给侧与需求侧存在的随机性问题、储能装置与微网系统之间的协调运行问题及不同能源之间的品位问题。同时,通过将FMEA分析法与蒙特卡洛模拟法相结合的方式,量化了不同能源之间的耦合逻辑关系,体现了能源生产、存储及使用环节中的时序特性,完善可靠性评估方法。最后,计算了不同运行模式下综合能源微网的年可靠性,以及在典型场景与典型时段内的可靠性指标,从而验证了本文所提方法的有效性及实用性,主要结论如下。

1)以电力系统为例,传统可靠性计算通常是以负荷峰值为基准进行评估,没有考虑多能源耦合与时序特性的影响,方法很难满足能源互联网背景下多能源系统规划的需求。

2)考虑到以电、热、冷能为代表的多能源负荷的时序特性不同,负荷的供能周期及峰谷差存在同时率的问题。因此,本文所提出的可靠性评估方法进一步考虑了微网系统“源—荷—储”环节的时序特性及运行因素,保障可靠性评估模型的科学性。

3)从用户需求侧的角度出发,同一个用户可能具有多种能源的需求,在不同时段内用户对于能源的需求程度也不尽相同。因此,研究多能耦合集成系统的可靠性评估方法以响应并兼顾多能耦合情况下用户对于多种能源的需求十分必要。

4)考虑多能耦合的综合可靠性评价方法也可以为供能机组的预防性检修与维护提供参考。

在未来的研究中,将会进一步细化系统内的网架结构,分析不同能源系统供给与运行方式对多能源耦合系统可靠性的影响,从而进一步完善综合可靠性评估模型及方法。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 董朝阳,赵俊华,文福拴,等.从智能电网到能源互联网:基本概念与研究框架[J].电力系统自动化,2014,38(15):1-11.DOI:10.7500/AEPS20140613007.

DONG Zhaoyang, ZHAO Junhua, WEN Fushuan, et al. From smart grid to Energy Internet: basic concept and research framework[J]. Automation of Electric Power Systems, 2014, 38(15): 1-11. DOI: 10.7500/AEPS20140613007.

[2] GEIDL M, KOEPPEL G, FAVRE P, et al. Energy hubs for the future[J]. IEEE Power & Energy Magazine, 2007, 5(1): 24-30.

[3] WU J, YAN J, JIA H, et al. Integrated energy systems[J]. Applied Energy, 2016, 167: 155-157.

[4] LASSETER R, AKHIL A, MAMAY C, et al. White paper on integration of distributed energy resources-the CERTS microgrid concept[R]. Office of Scientific & Technologies, the US Department of Energy, 2002.

[5] LASSETER R H, PAIGI P. Microgrid: a conceptual solution[C]// IEEE Power Electronics Specialists Conference, June 20-25, 2004, Aachen, Germany: 4285-4290.

[6] LI H, ESEYE A T, ZHANG J, et al. Optimal energy management for industrial microgrids with high-penetration renewables[J]. Protection & Control of Modern Power Systems, 2017, 2(1): 12.

[7] WANG P, BILLINTON R, GOEL L. Probability distribution evaluation of distribution system reliability indices using a time sequential simulation technique[C]// Canadian Conference on Electrical and Computer Engineering, May 7-10, 2000, Halifax, Canada: 760-764.

[8] BILLINTON R, WANG P. Teaching distribution system reliability evaluation using Monte Carlo simulation[J]. IEEE Transactions on Power Systems, 1999, 14(2): 397-403.

[9] CHE L, ZHANG X, SHAHIDEHPOUR M, et al. Optimal interconnection planning of community microgrids with renewable energy sources[J]. IEEE Transactions on Smart Grid, 2017, 8(3): 1054-1063.

[10] XU X, MITRA J, WANG T, et al. An evaluation strategy for microgrid reliability considering the effects of protection system[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 1989-1997.

[11] MOEINI A M, FARAIN H, FOTUHI F M, et al. Generalized analytical approach to assess reliability of renewable-based energy hubs[J]. IEEE Transactions on Power Systems, 2016, 32(1): 368-377.

[12] LI G, BIE Z, KOU Y, et al. Reliability evaluation of integrated energy systems based on smart agent communication[J]. Applied Energy, 2016, 167: 397-406.

[13] KOEPPEL G, ANDRSSON G. Reliability modeling of multi-carrier energy systems[J]. Energy, 2009, 34(3): 235-244.

[14] KOEPPEL G, ANDERSSON G. The influence of combined power, gas, and thermal networks on the reliability of supply[C]// The Sixth World Energy System Conference, July 10-12, 2006, Torino, Italy: 646-651.

[15] CHAUDRY M, WU J, JENKINS N. A sequential Monte Carlo model of the combined GB gas and electricity network[J]. Energy Policy, 2013, 62(9): 473-483.

[16] CONTI S, NICOLOSI R, RIZZO S A. Generalized systematic approach to assess distribution system reliability with renewable distributed generators and microgrids[J]. IEEE Transactions on Power Delivery, 2012, 27(1): 261-270.

[17] 王旭东,林济铿.基于网络化简的含分布式电源的配电网可靠性分析[J].电力系统自动化,2010,34(4):38-43.

WANG Xudong, LIN Jikeng. Reliability evaluation based on network simplification for the distribution system with distributed generation[J]. Automation of Electric Power Systems, 2010, 34(4): 38-43.

[18] XU X, HOU K, JIA H, et al. A reliability assessment approach for the urban energy system and its application in energy hub planning[C]// IEEE Power & Energy Society General Meeting, July 26-30, 2015, Denver, USA.

[19] 徐科,刘洪,田喆,等.区域分布式供能系统经济性概率分析[J].电力建设,2017,38(2):138-146.

XU Ke, LIU Hong, TIAN Zhe, et al. Economic probability analysis of urban distributed energy supply system[J]. Electric Power Construction, 2017, 38(2): 138-146.

[20] 陈健,刘玉田,张文,等.基于博弈论的配电网中多级微电网优化配置分析[J].电力系统自动化,2016,40(1):45-52.DOI:10.7500/AEPS20150130005.

CHEN Jian, LIU Yutian, ZHANG Wen, et al. Optimal sizing analysis of multilevel microgrids in distribution network based on game theory[J]. Automation of Electric Power Systems, 2016, 40(1): 45-52. DOI: 10.7500/AEPS20150130005.

[21] WANG Peng, BILLINTON R. Time sequential distribution system reliability worth analysis considering time varying load and cost models[J]. IEEE Transactions on Power Delivery, 1999, 14(3): 1046-1051.

[22] NIKMEHR N, RAVADANEGH S N. Reliability evaluation of multi-microgrids considering optimal operation of small scale energy zones under load-generation uncertainties[J]. International Journal of Electrical Power & Energy Systems, 2016, 78: 80-87.

[23] DUFFIE J A, BECKMAN W A. Solar engineering of thermal processes[M]. New York, USA: Wiley, 1991.

[24] GHIANI E, VERTUCCIO C, PILO F. Optimal sizing and management of a smart microgrid for prevailing self-consumption[C]// 2015 IEEE Eindhoven PowerTech, June 29-July 2, 2015, Eindhoven, Netherlands: 639-645.

[25] ERDINC O. Economic impacts of small-scale own generating and storage units, and electric vehicles under different demand response strategies for smart households[J]. Applied Energy, 2014, 126: 142-150.

[26] 赵波,包侃侃,徐志成,等.考虑需求侧响应的光储并网型微电网优化配置[J].中国电机工程学报,2015,35(21):5465-5474.

ZHAO Bo, BAO Kankan, XU Zhicheng, et al. Optimal sizing for grid-connected PV-and-storage microgrid considering demand response[J]. Proceedings of the CSEE, 2015, 35(21): 5465-5474.

[27] 吴雄,王秀丽,李骏,等.风电储能混合系统的联合调度模型及求解[J].中国电机工程学报,2013,33(13):10-17.

WU Xiong, WANG Xiuli, LI Jun, et al. A joint operation model and solution for hybrid wind energy storage systems[J]. Proceedings of the CSEE, 2013, 33(13): 10-17.