独立模式下微网多能存储系统优化配置

崔明勇, 王楚通, 王玉翠, 卢志刚, 陈 辰

(燕山大学电气工程学院, 河北省秦皇岛市 066004)

0 引言

随着传统化石能源的日渐枯竭,能源互联网的建设得到了广泛关注[1]。而可以应用到孤立海岛、城市农村集中住宅区、工厂、脱离主网的偏远地区等区域的综合能源微网将成为能源互联网的重要组成部分[2]。综合能源微网的概念是在微网概念上发展而来,一般包含多种能源形式,利用物联网技术和信息技术对区域内的所有供能设备源统一整合并实施调度,以达到对区域冷热电负荷进行优化供能,提升能源利用效率的效果[3-4]。

但是,以风光为代表的可再生能源又有很强的间歇性和随机波动性,往往会导致弃风、弃光等现象的产生。尤其是在供热期间,热电联产机组“以热定电”的运行模式会降低整个微网电能的调峰能力,甚至造成大量的弃风[5]。在微网中加装单一的储能系统后会减少一定的弃风量,但往往热、电等多能源互相转换会造成一定的能量损失,且供暖期热电联产机组“以热定电”的模式导致经济性不高。同时,储电系统制造成本高昂,能量大规模存储的损失较大。而储热、气系统可大规模存储能量,但系统惯性较电网大,能量传递慢。因此,为了消纳可再生能源,增强微网的灵活性,达到多种储能形式优势互补的目的,微网中引入了可用于多能存储的储能系统。

能量的存储作用就叫储能,主要有储电、储热、储气、复合储能(电转气(P2G)、液氢超导磁储能(SMES)等)几种形式[6]。本文主要探讨储电和储热两种形式的储能系统。微网技术的深入研究推动了储电技术的发展。电储能技术可用于平抑可再生能源发电的短时功率波动,跟踪调度计划出力,改善可再生能源发电接入电网的电能品质,满足新能源灵活接入优化负荷,进行削峰填谷,提高系统自身调节能力,实现对负荷的管理并获得经济效益[7]。对于电储能系统的配置方面,有大量学者进行了研究。文献[8]建立储电系统最优的配置模型,并计及整个微网的稳定性。文献[9-10]以微网最优经济运行为研究对象,研究了铅酸蓄电池充放电深度和次数对其寿命的影响,建立了微网最优经济运行模型。文献[11-13]建立了混合储能优化配置模型。

在储热技术上,显热储热和相变储热都得到了较快的发展,并且有着广泛的实际工程应用。文献[14]通过研究加装储热装置和碳捕集装置的热电联产机组对经济和低碳性的影响,给出了调度策略,为电网调度提供一定的参考依据。文献[15]构建了含储热热电联产机组与电锅炉的弃风消纳协调调度模型。文献[16]介绍了包含大容量储热的电—热联合系统关键技术的研究工作。

但是,对于多能存储系统综合配置的研究较少。文献[17]针对城市社区的特点,提出一种基于压缩空气储能的微能源网架构,结合社区用能数据对其中的主要设备进行容量配置,并对其中的储能子系统,包括电储能和热储能进行具体的配套设计和运行方式分析。文献[18]提出一种基于氢储能的风电与煤化工多能耦合系统设备投资规划优化方法。文献[19]针对包括P2G的多能源系统的市场均衡问题进行分析,其中包括对P2G设备、储气装置的建模。文献[20]将含P2G的多源储能型微网系统划分为供给侧、转换组件和负荷侧三个部分进行建模,在此基础上建立基于经济最优的微网系统日前优化调度模型。文献[21]基于能源互联网的特征,给出了广义电力储能的定义,指出了储能在能源互联网应用中的几项关键技术,并提出储能与能量转换装置的集成设计和协调配置,是能源互联网中有待解决的一项关键技术。

以上文献在微网储能系统配置方面取得了一定进展,但通过阅读并比较此类文献,发现有以下几个问题相对突出。

1)储热系统的额定功率和容量在储能系统的配置中没有考虑。

2)考虑蓄电池寿命的情况下,并未计及供暖期和非供暖期蓄电池荷电状态曲线的不同。

3)多数文献的优化配置算法未与功率分配策略结合,导致了大量冗余解。

本文针对以上问题,构建了独立模式下的综合能源微网多能存储系统优化配置模型,提出了包含储电系统和储热系统的额定功率、容量的配置方法,其中,储电系统模型计及供暖期与非供暖期蓄电池寿命。模型以经济性作为指标,考虑热电机组的热电耦合相关约束,采用基于机组出力和储能系统功率分配策略的细菌群体趋药性(BCC)算法模型进行求解。并探讨了加装储能系统的热电联产机组的运行特性。

1 各电源运行特性及风电消纳原理

1.1 典型微网结构

典型微网的结构配置主要包含风机(wind turbine,WT)、常规火电机组、热电联产机组、电储能(electrical energy storage,ESS)和热储能(heat storage,HS)等单元,且网内各单元均由微网中央控制器(microgrid central controller,MGCC)进行统一控制和信息传达。

1.2 热电联产机组原理

常见的热电联产机组按其特性不同可以分为4类[22]。本文以最常见的抽汽式热电联产机组为例,其电热特性如图1所示。

由图1可知,汽轮机纯凝工况下的最大、最小电出力分别为Pmax和Pmin,随着抽汽量增加,电功率按一定弹性系数比例减小,在供热功率为hdot时,电功率的调节范围为[Pe,min,Pe,max],调节电出力能力十分有限。图1中γ表示当进汽量维持恒定时,多抽取单位供热热量时电功率的减少量。在纯凝工况下的发电功率、净发电功率以及热功率存在如下关系[14]:

图1 热电联产机组的电热特性Fig.1 Heat-electricity characteristic for combined heat and power units

P=Pe+γh

(1)

式中：Pe为热电联产机组电功率；h为热功率。

抽汽式热电联产机组的热特性可以表述为:

(2)

式中:hmax为机组的最大供热功率;Pmax和Pmin分别为热电联产机组在纯凝工况下的最大和最小发电功率。

在加装储能系统后,传统的热电联产机组运行将发生很大改变。首先,加入储热装置后热电联产机组在输出同一热功率情况下,电出力调节范围增大[15]。而储能电池的加入进一步增大了电出力的调节范围,可以有效解耦热电耦合特性,达到灵活调节热电联产机组出力的目的。

1.3 储能系统

1.3.1储电系统

储电系统主要有蓄电池、压缩空气储能、飞轮储能、超导储能、超级电容储能等形式。本文以应用最广泛的蓄电池为例。

蓄电池荷电状态(state of charge,SOC)是反映蓄电池剩余电量占其总容量比例的参数,一般用其与蓄电池充放电功率和容量的关系构建蓄电池模型。

充电过程为:

(3)

放电过程为:

(4)

式中:SSOC(t)为第t个时段结束时储能系统的荷电状态;SSOC(t-1)为第t-1个时段结束时储能系统的荷电状态;δ为储能系统的自放电率;Pc和Pd分别为储能系统的充、放电功率;ηc和ηd分别为储电系统的充、放电效率;Ce,max为储电系统的额定容量。

1.3.2储热系统

储热技术分为显热储热和相变储热。一般地,类比于储能电池,储热系统储热状态与其充放热功率和储热容量构建模型。

储热过程为:

(5)

放热过程为:

(6)

式中:HHS(t)为时段t的热储能容量;HHS(t-1)为t-1时段结束时的热储能容量;μ为热储能散热损失率;Qc(t),Qd(t)和ηhc,ηhd分别为时段t的吸放热功率及效率;Hhold为储热系统容量。

1.4 最优化储能系统配置原理

储能系统分为电储能系统(蓄电池)和热储能系统,储能系统的配置包括功率和容量配置。储电系统包括蓄电池、变流器等设备,所以投资成本分别以功率和容量两种形式结算。储热系统包括储热罐和导热材料等,所以投资成本同样以功率和容量两种形式结算。

储能系统的配置影响储能系统的投资费用、整个微网的运行费用、治污费用三个方面。配置较低的储能系统达不到系统预期的经济性和稳定性,不能有效降低运行费用,排放污染物含量较高。配置较高的储能系统投资费用较高,整体的维护费用也相对较高。因此,最优的储能系统的配置选择可以在投资费用、运行费用、治污费用三者间达到平衡点,即总的费用达到最小的储能系统配置。

1.5 储能电池寿命模型

储能电池的寿命受很多因素的影响,包括电池的放电深度、倍率性能、充放电截止电压和环境温度等。上文已提及储能电池的最大功率取额定值,因此暂且不考虑电池的倍率性能对其寿命的影响。由于文中已设定了储能电池的容量取值范围,暂且不考虑电池的充放电截止电压对其寿命的影响。环境温度视为室温,暂且不考虑其对电池寿命的影响。经过一些简化,本文仅考虑放电深度对储能电池寿命的影响,因此可以利用雨流计数法预估储能电池寿命。

雨流计数法又可称为“塔顶法”,是由英国的Matsuiski和Endo两位工程师提出的,雨流计数法主要用于工程界,特别在疲劳寿命计算中应用非常广泛。

常用的拟合方法有N阶函数法、幂函数法和分段拟合法等,本文采用文献[10]中的四阶函数表征循环寿命与放电深度的关系,有

14 122DoD+5 112

(7)

式中:Ncyc,i为第i次循环周期对应的最大循环次数;DoD为该循环周期的放电深度。

由于本文考虑的储能系统包含储电和储热两方面,在供暖期和非供暖期,加装储热系统后,储能电池的SOC曲线有明显差异,因此对传统雨流计数法计算寿命的方法作进一步改进。设供暖期是11月至次年3月,共120 d;非供暖期是4月至10月,共245 d,有

(8)

(9)

(10)

式中:dloss和dwinloss分别为非供暖期和供暖期一天的电储能系统寿命折损率;θ为周期系数,全周期为1,半周期为0.5;T为寿命周期。

这样,通过构建供暖期和非供暖期中典型日的一天中蓄电池的充放电曲线,可以估算出储能系统的寿命。

1.6 独立微网负荷特性对储能系统配置的影响

独立微网的用能特性和负荷特性会影响储能系统的配置,具体表现如下。

独立微网耗能较大时,储能系统的最优化配置相对升高,耗能较小时,储能系统的最优化配置相对降低。这是由于耗能大小决定了所需储能系统的额定功率和容量。

独立微网的负荷特性主要影响储能系统优化配置过程中功率和容量的寻优范围、功率分配策略的选择。以下分析微网中主要负荷类型对储能系统配置的影响。

1)居民负荷:负荷特性主要与居民活动有关,电负荷在午间和晚间为高峰时段,上午与下午时段为平时段,凌晨时段一般为谷时段,波动大,规模较小。供暖期热负荷大部分时段维持在恒定值,只在午间由于气温因素,热负荷需求量较低。由于居民负荷非重要负荷,可以转移和中断,因此储能系统寻优范围主要与微网耗能大小有关。功率分配策略主要依据为风机净功率和负荷特性。

2)商业负荷:负荷特性主要与商业特性有关。电负荷在白天阶段为高峰时段,晚上为低谷时段,波动较小,规模中等。供暖期热负荷在白天一般为恒定值,晚上热负荷需求较低。由于商业负荷也非重要负荷,因此,储能系统寻优范围主要与微网耗能大小有关。功率分配策略主要依据为风机净功率和负荷特性。

3)工业负荷:负荷特性主要与生产性质和生产计划有关,工业电负荷可分为产线负荷和重要负荷,规模较大。其中,产线负荷是指主要生产设备所对应的负荷。除产线设备外,实际的工厂里必须安装相应的辅助设备来保证整个生产过程的安全进行,如工厂中的冷却塔和各类服务器。当此类辅助生产设备突然断电时,如不能及时恢复供电,则可能会对整个系统造成严重的损害。因此,把此类负荷列为重要负荷[23]。在独立微网中,必须保证重要负荷的供电。工业负荷中,电负荷一般维持在恒定值,只在工人换班和用餐时间由于部分生产设备的关闭出现明显的负荷低谷。供暖期热负荷同样也维持在恒定值。因此,为了保证重要负荷的供给,储电系统额定功率和容量配置寻优范围应根据工厂耗能大小与重要负荷需求量设定最低限制,同时相应确定SOC约束范围。功率分配策略主要依据为生产计划。

1.7 储能消纳风电原理

独立型微网中,在冬季供暖期由于夜间风电过剩,且无法并网,而热电机组由于供热需求,使电出力无法下调,从而使风电难以消纳,造成了严重的弃风。微网中加装储热装置后,在非弃风时段,热电机组满足热负荷需求的基础上,也向储热装置蓄热,而在弃风时段,为了消纳风电,可以降低热电机组出力。因此,导致的供热不足部分则由储热系统放热补充。同时,储电系统可进一步存储弃风阶段的多余电量,从而接纳更多风电,最大程度地减少弃风。

2 储能系统优化配置模型

依据微网中经济性最高,利益最大化的原则,本文以系统的经济总成本最小为目标,建立了包含储能系统投资成本、微网运行成本、治污成本的规划系统模型,如图2所示。

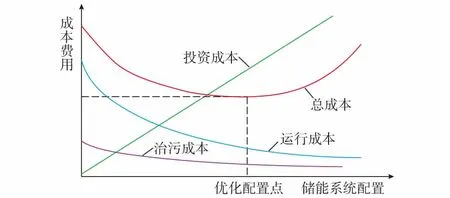
图2 储能系统优化配置模型Fig.2 Optimal configuration model of energy storage system

2.1 目标函数

在储能系统优化配置问题中,以经济性作为优化目标,提出的目标函数如下:

Ctotal=min(Cinv+Copt+Cpol)

(11)

Cinv=αPB,R+βCe,max+χhB,R+δCh,max

(12)

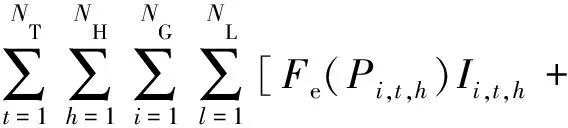
Fh(Pl,t,h)Ll,t,h+SU,t,h+SD,t,h]

(13)

(14)

式中:Ctotal为储能系统规划周期内微网的总成本;Cinv为储能系统的投资费用;Copt为微网运行费用;Cpol为微网治污成本;α为蓄电池的单位功率投资系数;β为蓄电池的单位容量投资系数;χ为储热系统的单位功率投资系数;δ为储热系统的单位容量投资系数;PB,R为蓄电池的最大功率;hB,R和Ch,max分别为储热系统的最大功率和最大容量;NT为总天数;NH为总小时数;NG为总的常规火电机组数;NL为总的热电联产机组数;Pi,t,h为常规机组i在时段t内产生的功率,Fe为该功率与费用的函数关系;Ii,t,h为分布式电源是否工作的状态指数,其值为1表示工作,其值为0表示不工作;Pl,t,h为热电联产机组l在时段t内产生的功率,Fh为该功率与费用的函数关系;Ll,t,h为热电联产机组l是否工作的状态指数,其值为1表示工作,其值为0表示不工作;SU,t,h和SD,t,h分别为发电机组的启停机费用;αk为污染物k的治理费用系数;βk为污染物k的排放系数;NK为污染物总量；pdie(t)为某时段某机组发出的功率。

其中,对于蓄电池的单位容量投资系数,有

(15)

式中:CE为单位容量投资总成本;Cm为年单位容量设备的维修、维护费用和装置处置费用之和;Tlife为估算的储能系统寿命。这样将这些费用平摊到储能系统的周期寿命中,可以得到规划周期内的单位容量投资系数。

发电成本一般可以表示为发电功率的二次函数的形式。常规火电机组和热电联产机组的功率成本函数分别为:

(16)

al(Pe，i,t+γlhl,t,h)2+bl(Pe,i,t+γlhl,t,h)+cl

(17)

式中:ai,bi,ci和al,bl,cl分别为常规机组和热电联产机组的成本系数。

2.2 约束条件

2.2.1系统约束

1)电功率平衡约束

(18)

式中:NR为新能源数量;Pi,t,h为新能源产生的功率;PESS为储能系统充电或者放电的功率,充电为负值,放电为正值;Pload,t,h为t时段负荷所需的功率。

2)供热平衡约束

(19)

式中:hl,t,h为热电联产机组l在t时段的热功率;hhs为该时段储热系统的储、放热功率,放热为正值,储热为负值;hload,t,h为系统该时段的热负荷。

3)风电出力约束

(20)

式中:Pw,max为风力发电机的额定功率;vci,vr,vco分别为风机的切入风速、额定风速和切出风速;vt,h为某时段的风速。

2.2.2机组约束

1)机组出力上下限约束

pi,min≤pi,t≤pi,max

(21)

式中:pi,min和pi,max分别为机组的最小和最大电出力。

2)抽汽式机组热出力上、下限约束

0≤hl,t,h≤hl,max

(22)

式中:hl,max为机组l热出力的最大限值。

3)机组的总功率爬坡约束

Pi,t,h-Pi,t,h-1≤Δpu,i

(23)

Pi,t,h-1-Pi,t,h≤Δpd,i

(24)

式中:Δpu,i和Δpd,i分别为机组i的最大上、下爬坡出力。

4)抽汽式机组的热爬坡约束

hl,t,h-hl,t,h-1≤Δhu,l

(25)

hl,t,h-1-hl,t,h≤Δhd,l

(26)

式中:Δhu,l和Δhd,l分别为抽汽式机组单位时间内的热功率最大变化量。

2.2.3储能系统约束

1)储能电池上下限约束

SSOC,min≤SSOC≤SSOC,max

(27)

式中:SSOC,min和SSOC,max分别为储能电池荷电状态的最小值和最大值。

2)储热系统上下限约束

HHS,min≤HHS≤HHS,max

(28)

式中:HHS,min和HHS,max分别为储热系统储热状态的最小值和最大值。

2.2.4自给自足概率约束

在微网的独立运行模式下,满足负荷需求,达到系统稳定性尤为重要。由此,引入了自给自足概率的概念。通过对是否在规划期内达到负荷需求的概率进行约束来配置储能系统,并同时计及负荷与风力出力预测误差。

对于电负荷:

(29)

对于热负荷:

(30)

式中:PSS,e和PSS,h分别为微网中电负荷与热负荷的自给自足概率;Δw,Δd,Δh分别为满足正态分布的风电出力预测误差、电负荷误差、热负荷误差。

3 模型求解

BCC算法由细菌趋药性算法(BC)改进而来,本文采用的是基于机组出力和储能系统功率分配策略的BCC算法。

每一行4个细菌分别代表储电系统额定功率和容量,储热系统额定功率和容量,为了在微网中合理协调系统内的电源出力来满足负荷的需要。确保各个时段为电源出力和负荷需求的实时功率平衡,防止储能系统的过充过放,实现对微网各分布式电源的优化调度。在实际规划过程中,往往需要选取一套合理的功率分配策略,这可以有效提高可行解的产生效率,进而提高算法性能。

储能系统在规划周期一般分为供暖期与非供暖期,在非供暖期,热电联产机组和储热系统停止运行,在供暖期,热电联产机组和储热系统投入系统运行。

在非供暖期,微网中优先利用风电,多余风电通过储能电池存储起来,风电不足,则通过常规机组补足出力需求。

在供暖期,由于储热系统充放热的损耗成本远低于蓄电池充放电的损耗成本,所以优先利用储热系统消纳风电。本文主要研究的负荷类型为居民负荷,具体运行策略如下。

首先,判断该时段是否在弃风阶段,判断依据是风力出力是否满足电负荷需求。若在弃风阶段,储热系统放热,剩余热负荷需求由热电联产机组补足,电负荷优先消耗风电和热电联产机组的出力,多余电能通过储能电池存储起来。若在非弃风阶段,热电机组在满足热负荷需求的同时,给储热系统储热,再根据电力负荷判断储电系统的充放电需求,电力不足则通过常规火电机组补足。具体步骤如附录A图A1。

4 算例仿真

4.1 算例数据

本文采用6机组系统进行仿真,系统由3台常规火电机组、2台抽汽式热电机组和1台风力发电机构成,具体参数见附录A表A1,系统负荷分为供暖期和非供暖期,其与风电功率通过选取某海岛历史数据进行预测,该海岛负荷主要为居民负荷。煤耗特性参数及电热输出运行参数见附录A表A1,污染物及治污成本系数见附录A表A2[24],自给自足概率要求都取90%,自给自足概率预测误差正态分布Δw,Δd,Δh分别取(0,144)kW,(0,256)kW,(0,256)kW,储能电池单位功率年投资成本系数α为240元/(kW·a),容量投资总成本CE为80元/(kW·h),年单位容量设备的维修、维护费用和装置处置费用之和Cm为30元/((kW·h)·a),储热系统的年单位功率投资系数为192元/(kW·a),年单位容量投资系数为9元/((kW·h)·a)。微网规划周期取1 a,为防止过充过放,SOC上下限分别取0.9和0.2。HHS上下限分别取0.9和0.1;初始SOC设置为0.2,供暖期初始HHS设置为0.5;储能系统的自放电率、自放热率均为0.01,充放电效率、充放热效率均为0.75;热电机组的γ为0.9。细菌个数为50,最大迭代次数为100,初始精度εbegin=2,最终精度εend=10-2,精度更新常数d=1.25,每个细菌移动速度v=1。

为了对比分析储能系统配置后对系统产生的经济效益,设置了3种不同场景。

场景1:系统中无储能设备。

场景2:系统中加装随机配置的储能系统。

场景3:系统中配置优化后的储能系统。

4.2 优化结果分析

选取供暖与非供暖典型日,储能电池理想状态下(即不受容量限制,只与负荷需求有关)SOC曲线如附录A图A2和图A3所示。由图可知,在非供暖期,有4个半周期,放电深度分别为0.6,0.6,0.2,0.2。供暖期2个半周期,放电深度分别为0.4和0.4,经计算可知每年的寿命折损率约为0.45。在供暖期,由于主要通过储热系统消纳风电,所以储能电池SOC变化较小,经过估算可以得出储能电池寿命大约为2.2 a,进而得出储能电池单位容量年投资系数β为66元/((kW·h)·a)。

场景1总成本为17 119.02万元,其中包含运行成本17 118万元,治污成本1.02万元。电负荷自给自足的概率为65%,热负荷自给自足的概率为87%,不满足要求。在非供暖期,火电机组1全时段运行,在出力不足的时段,由火电机组2和3补足。在供暖期,热电机组运行,优先满足热负荷,由于抽汽式机组“以热定电”的模式,在冬季风能资源充足的情况下,会造成大量弃风。

场景2随机选取储能电池3 MW/5 MW·h、储热系统1 MW/6 MW·h的配置,总成本为7 936.4万元,其中储能系统的投资成本为100.8万元,微网的运行成本和治污成本分别为7 834.6万元和0.97万元。与场景1相比,总成本同比减少53%,总成本减少的主要原因是在配置储能系统后,由于储能电池可以削峰填谷、优化出力调度,减少风电损失,以及储热系统在供暖期可以增大风电的利用率,避免弃风的产生,使得总成本减少。此方案下,电负荷自给自足的概率为97%,热负荷自给自足的概率为99%,满足系统设定的自给自足概率。

场景3利用文中提出的储能系统优化配置方法,寻求最优化配置,得出最优配置为储能电池2.6 MW/9.1 MW·h、储热系统2.2 MW/10 MW·h的配置,即所寻求的最优化配置。该配置下,总成本为7 775.1万元,与场景1相比,总成本同比减少54%,与场景2相比,总成本同比减少2%,其中储能系统投资成本为154.8万元,微网的运行成本和治污成本分别为7 619.3万元和0.93万元。此配置下的电、热负荷自给自足的概率均为99%。与场景2相比,总成本减少的原因是系统配置了优化后的储能系统,可以更有效地优化系统出力,减少弃风。具体对比结果见表1。

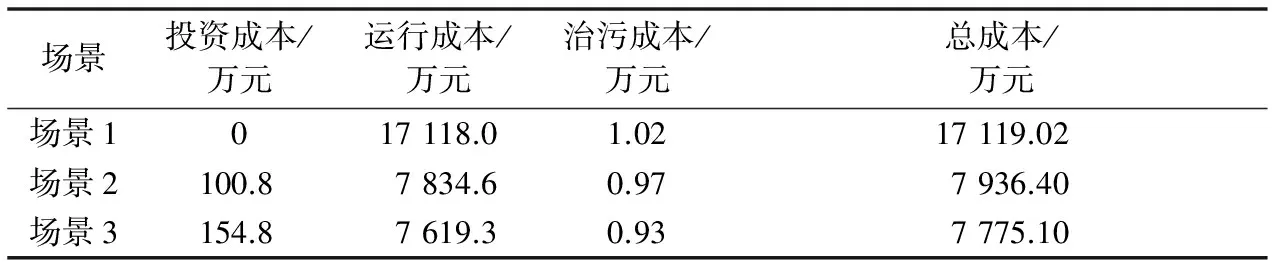
表1 不同场景的成本Table 1 Cost in different scenes

从图3(a)可以看出,微网在弃风阶段储能电池充电,在非弃风阶段,利用完风电之后,优先通过储能电池补足出力,可有效削峰填谷,减少能源损耗。

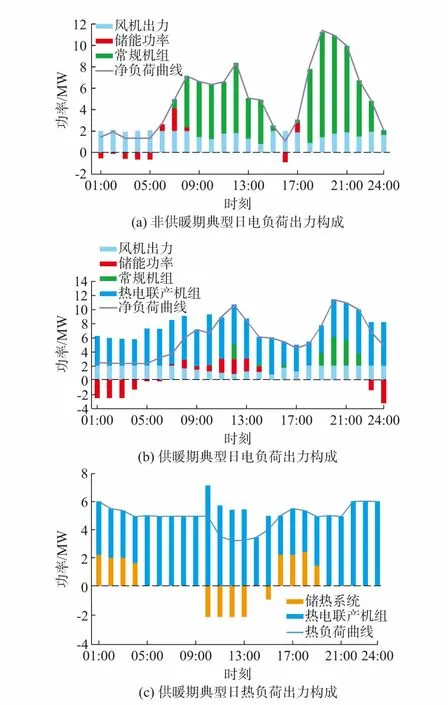
图3 供暖期、非供暖期典型日负荷出力构成Fig.3 Composition of load output on a typical day during the heating and non-heating periods

图3(b)和(c)是供暖期电、热出力情况,在弃风阶段,储热系统释放热能与热电联产机组共同满足热负荷,此时热电联产机组出力较小,可以优先利用风能,减少弃风。在这种情况下,电能有时仍有大量剩余,此时可以利用储能电池存储电能。在非弃风阶段,热电机组在满足热负荷的同时,给储热系统储热,再根据电力负荷判断储电系统的充放电需求。可以看出,由于在微网中引入了多能存储系统,增加了微网的灵活性和系统收益,减少了弃风的产生。

在非供暖期的运行成本只考虑储能电池的功率和容量。如图4所示,选取以1 MW为步长的一系列数据,可以看出,随着系统配置的增高,系统运行费用逐渐减少,而投资费用随之增加,治污费用随之减少。而供暖期考虑储能电池和储热系统整体配置,随着配置的增高,储能系统投资费用增高,微网运行费用、治污费用也随之减少。

图4 非供暖期运行成本与储能系统配置的关系Fig.4 Relationship between operation cost and energy storage system sizing during the non-heating period

4.3 风电消纳作用分析

附录B图B1为某供暖期典型日不同场景下的弃风量,可以看到场景1下的弃风量总量达39.11 MW。原因是在供暖期热电联产机组“以热定电”的生产模式,使供热导致的系统强迫电出力过高。在加装储能后,场景2和场景3的弃风量分别为8.19 MW和7.84 MW,弃风量大大减小。可见,储能系统的存在使得风电接纳量明显提高,对于系统整体的经济性起到了积极的作用。

4.4 与传统优化配置方法的对比分析

在比较分析过程中,设立以下场景。

场景4:系统中加装传统优化配置方法的储能系统。

传统储能系统优化配置方法与本文配置方法主要有以下3点不同。

1)未考虑其他储能形式的配置,如储热系统的优化配置。

2)估算储电系统寿命未考虑SOC曲线供暖期和非供暖期的不同。

3)在优化算法中未与功率分配策略相结合。

由于第1点主要是研究对象的不同,因此主要分析第2点和第3点。

传统配置方法估算储能电池寿命时,一般选取某典型日的SOC曲线。这里,选取典型非供暖期SOC曲线,如附录A图A2所示,可得4个半周期放电深度分别为0.6,0.6,0.2,0.2,经计算得到每年损耗率为0.55,估算出储电系统寿命约为1.8 a。计算出该结果的原因主要是未考虑供暖期SOC曲线与非供暖期的不同,在供暖期由于主要通过储热系统的充、放热作用消纳弃风,使得储能电池SOC曲线变化较小。因此,利用传统方法估算储能电池寿命产生了一定误差,造成之后投资成本计算不准确。

其次,在传统优化配置算法中,主要通过算法中功率平衡调节程序来保证有功出力平衡,但是这往往会造成大量冗余解的产生,使求解效率降低。为了比较两种算法,在其他条件相同的情况下,分别用传统BCC算法和考虑功率分配策略的BCC算法两种算法求解,并分别选取同一行菌群,在迭代1次、5次、10次、50次时设置断点,具体分析了供暖期典型日某一时段的电出力构成,结果如附录B图B2和图B3所示。

由附录B图B2可知,在第1次迭代时由于传统配置算法在约束范围内的随机取值,造成了有功功率的不平衡,第5次迭代虽然满足了功率平衡,但是由于该阶段为弃风阶段,储能电池状态应为存储电能,不符合实际运行工况。第10次迭代未寻得最优解。直到第50次迭代才取得最优解。而由图B3可知,与功率分配策略相结合的算法从第1次迭代时就满足实际运行工况,使得求解效率提高,在第10次迭代时就寻得了最优解。此外,冗余解还在以下情形产生:储能充放功率大于储能系统上阶段剩余容量、供暖期优先利用常规机组出力等。而与功率分配策略相结合的算法由于预先的设定,规避了冗余解的产生,提高了求解效率。

4.5 储能系统投资灵敏度分析

相对于储能系统的年单位容量投资,年单位功率投资系数更大,本节主要分析储电系统功率单位年投资系数对储电系统最优化配置和总成本的影响。在其他成本系数不变的情况下,取一系列数据,得出的结果如附录B图B4所示。可以看出,当α较小时,由于投资单位成本较低,储电系统最优配置功率较大,这也同时给系统带来了收益。随着α的增大,投资单位成本增加,功率最优化配置增大,而系统收益也由于储能系统配置降低而减少。而其他成本系数也有类似影响。

5 结论

本文提出了微网中储能系统优化配置的模型,得到如下结论。

1)微网中储能系统的配置可以影响储能系统的投资成本以及整个微网的运行成本和治污成本,且作为系统运行中的约束,影响整个微网功率分配策略的选择。因此,选择更为合理的储能系统配置可以提高新能源利用率,增加系统收益。

2)储能系统的合理配置能够在一定程度上避免冬季供暖期因热电联产机组“以热定电”模式强迫电出力而导致的弃风,进而提高独立微网整体的经济性和低碳性。

进一步的研究应考虑综合能源微网中储电、储气、储热的配置和相互间的耦合关系,以及P2G、液氢SMES等复合储能、能量转换装置在微网中的规划配置。在已有模型中,为了更精确估算储能系统的寿命,可以进一步考虑预测寿命随实际情况变化的修正模型。同时,本文主要研究对象是独立型微网,可以继续展开对并网型微网的研究。

本文研究得到燕山大学青年教师自主研究计划课题研究项目(15LGA005)的资助,谨此致谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] RIFKIN J. The third industrial revolution: how lateral power is transforming energy, the economy, and the world[J]. Survival, 2012, 2(2): 67-68.

[2] 田世明,栾文鹏,张东霞,等.能源互联网技术形态与关键技术[J].中国电机工程学报,2015,35(14):3482-3494.

TIAN Shiming, LUAN Wenpeng, ZHANG Dongxia, et al. Technical forms and key technologies on energy internet[J]. Proceedings of the CSEE, 2015, 35(14): 3482-3494.

[3] 李洋,吴鸣,周海明,等.基于全能流模型的区域多能源系统若干问题探讨[J].电网技术,2015,39(8):2230-2237.

LI Yang, WU Ming, ZHOU Haiming, et al. Study on some key problems related to regional multi energy system based on universal flow model[J]. Power System Technology, 2015, 39(8): 2230-2237.

[4] 马腾飞,吴俊勇,郝亮亮.含冷热电三联供的微能源网能量流计算及综合仿真[J].电力系统自动化,2016,40(23):22-27.DOI:10.7500/AEPS20160426005.

MA Tengfei, WU Junyong, HAO Liangliang. Energy flow calculation and integrated simulation of micro-energy grid with combined cooling, heating and power[J]. Automation of Electric Power Systems, 2016, 40(23): 22-27. DOI: 10.7500/AEPS20160426005.

[5] 郭宇航,胡博,万凌云,等.含热泵的热电联产型微电网短期最优经济运行[J].电力系统自动化,2015,39(14):16-22.DOI:10.7500/AEPS20141127011.

GUO Yuhang, HU Bo, WAN Lingyun, et al. Optimal economic short-term scheduling of CHP microgrid incorporating heat pump[J]. Automation of Electric Power Systems, 2015, 39(14): 16-22. DOI: 10.7500/AEPS20141127011.

[6] BEAUDIN M, ZAREIPOUR H, SCHELLENBERG A, et al, Chapter 1: energy storage for mitigating the variability of renewable electricity sources[M]// Energy Storage for Smart Grids. Amsterdam, Netherlands: Elsevier Inc., 2015: 1-33.

[7] 周林,黄勇,郭珂,等.微电网储能技术研究综述[J].电力系统保护与控制,2011,39(7):147-152.

ZHOU Lin, HUANG Yong, GUO Ke, et al. A survey of energy storage technology for micro grid[J]. Power System Protection and Control, 2011, 39(7): 147-152.

[8] BAHRAMIRAD S, REDER W, KHODAEI A. Reliability-constrained optimal sizing of energy storage system in a microgrid[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 2056-2062.

[9] 李逢兵,谢开贵,张雪松,等.基于寿命量化的混合储能系统协调控制参数优化[J].电力系统自动化,2014,38(1):1-5.DOI:10.7500/AEPS20130503006.

LI Fengbing, XIE Kaigui, ZHANG Xuesong, et al. Optimization of coordinated control parameters for hybrid energy storage system based on life quantization[J]. Automation of Electric Power Systems, 2014, 38(1): 1-5. DOI: 10.7500/AEPS20130503006.

[10] 韩晓娟,程成,籍天明,等.计及电池使用寿命的混合储能系统容量优化模型[J].中国电机工程学报,2013,33(34):83-89.

HAN Xiaojuan, CHENG Cheng, JI Tianming, et al. Capacity optimal modeling of hybrid energy storage systems considering battery life[J]. Proceedings of the CSEE, 2013, 33(34): 83-89.

[11] 李龙云,胡博,谢开贵,等.基于离散傅里叶变换的孤岛型微电网混合储能优化配置[J].电力系统自动化,2016,40(12):108-116.DOI:10.7500/AEPS20150625011.

LI Longyun, HU Bo, XIE Kaigui, et al. Capacity optimization of hybrid energy storage systems in isolated microgrids based on discrete fourier transform[J]. Automation of Electric Power Systems, 2016, 40(12): 108-116. DOI: 10.7500/AEPS20150625011.

[12] XIE Qing, WANG Yanzhi, KIM Y, et al. Charge allocation in hybrid electrical energy storage systems[J]. IEEE Transactions on Computer—Aided Design of Integrated Circuits and Systems, 2013, 32(7): 1003-1016.

[13] 李成,杨秀,张美霞,等.基于成本分析的超级电容器和蓄电池混合储能优化配置方案[J].电力系统自动化,2013,37(18):20-24.

LI Cheng, YANG Xiu, ZHANG Meixia, et al. Optimal configuration scheme for hybrid energy storage system of super-capacitors and batteries based on cost analysis[J]. Automation of Electric Power Systems, 2013, 37(18): 20-24.

[14] 卢志刚,隋玉珊,冯涛,等.考虑储热装置与碳捕集设备的风电消纳低碳经济调度[J].电工技术学报,2016,31(17):41-51.

LU Zhigang, SUI Yushan, FENG Tao, et al. Wind power accommodation low-carbon economic dispatch considering heat accumulator and carbon capture devices[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 41-51.

[15] 崔杨,陈志,严干贵,等.基于含储热热电联产机组与电锅炉的弃风消纳协调调度模型[J].中国电机工程学报,2016,36(15):4072-4081.

CUI Yang, CHEN Zhi, YAN Gangui, et al. Coordinated wind power accommodating dispatch model based on electric boiler and CHP with thermal energy storage[J]. Proceedings of the CSEE, 2016, 36(15): 4072-4081.

[16] 徐飞,闵勇,陈磊,等.包含大容量储热的电-热联合系统[J].中国电机工程学报,2014,34(29):5063-5072.

XU Fei, MIN Yong, CHEN Lei, et al. Combined electricity-heat operation system containing large capacity thermal energy storage[J]. Proceedings of the CSEE, 2014, 34(29): 5063-5072.

[17] 薛小代,刘彬卉,汪雨辰,等.基于压缩空气储能的社区微能源网设计[J].中国电机工程学报,2016,36(12):3306-3314.

XUE Xiaodai, LIU Binhui, WANG Yuchen, et al. Micro energy network design for community based on compressed air energy storage[J]. Proceedings of the CSEE, 2016, 36(12): 3306-3314.

[18] 袁铁江,李国军,张增强,等.风电-氢储能与煤化工多能耦合系统设备投资规划优化建模[J].电工技术学报,2016,31(14):21-30.

YUAN Tiejiang, LI Guojun, ZHANG Zengqiang, et al. Optimal modeling on equipment investment planning of wind power-hydrogen energy storage and coal chemical pluripotent coupling system[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 21-30.

[19] 王业磊,赵俊华,文福拴,等.具有电转气功能的多能源系统的市场均衡分析[J].电力系统自动化,2015,39(21):1-10.

WANG Yelei, ZHAO Junhua, WEN Fushuan, et al. Market equilibrium of multi-energy system with power-to-gas functions[J]. Automation of Electric Power Systems, 2015, 39(21): 1-10.

[20] 陈沼宇,王丹,贾宏杰,等.考虑P2G多源储能型微网日前最优经济调度策略研究[J].中国电机工程学报,2017,37(11):3067-3077.

CHEN Zhaoyu, WANG Dan, JIA Hongjie, et al. Research on optimal day-ahead economic dispatching strategy for microgrid considering P2G and multi-source energy storage system[J]. Proceedings of the CSEE, 2017, 37(11): 3067-3077.

[21] 李建林,田立亭,来小康.能源互联网背景下的电力储能技术展望[J].电力系统自动化,2015,39(23):15-25.DOI:10.7500/AEPS20150906004.

LI Jianlin, TIAN Liting, LAI Xiaokang. Outlook of electrical energy storage technologies under Energy Internet background[J]. Automation of Electric Power Systems, 2015, 39(23): 15-25. DOI: 10.7500/AEPS20150906004.

[22] ROY P K, PAUL C, SULTANA S. Oppositional teaching learning based optimization approach for combined heat and power dispatch[J]. International Journal of Electrical Power & Energy Systems, 2014, 57(5): 392-403.

[23] 许健,刘念,于雷,等.计及重要负荷的工业光伏微电网储能优化配置[J].电力系统保护与控制,2016,44(9):29-37.

XU Jian, LIU Nian, YU Lei, et al. Optimal allocation of energy storage system of PV microgrid for industries considering important load[J]. Power System Protection and Control, 2016, 44(9): 29-37.

[24] 丁明,王波,赵波,等.独立风光柴储微网系统容量优化配置[J].电网技术,2013,37(3):575-581.

DING Ming, WANG Bo, ZHAO Bo, et al. Configuration optimization of capacity of standalone PV-wind-diesel-battery hybrid microgrid[J]. Power System Technology, 2013, 37(3): 575-581.