计及可靠性的电—气—热能量枢纽配置与运行优化

罗艳红, 梁佳丽, 杨东升, 周博文, 胡 博, 杨 玲

(1. 东北大学信息科学与工程学院, 辽宁省沈阳市 110819; 2. 国网葫芦岛供电公司, 辽宁省葫芦岛市 125000;3. 国网阜新供电公司, 辽宁省阜新市 123000)

0 引言

传统能源系统如电力系统、天然气系统、热力系统大多是分开规划、单独运行,彼此之间缺乏协调与配合,不利于供能系统的经济、高效运行。随着能源互联网的发展,电、气、热等多种能源之间的耦合与内部依赖显著增加,源—网—荷互动加强[1],多能源协同运行趋势日趋明显。多能源系统对于提升能源利用效率,降低能源成本,保障能源的安全、经济、高效和清洁供应具有重要意义[2-3]。多能源系统由多类异质能源系统组成,单个系统建模、分析和控制方法不同,使得多能源耦合运行变得越来越复杂[4-5]。能量枢纽是一个典型的多输入多输出、多级能量流和信息流融合的互联节点,集成包括可再生能源等各种形式的能源,为多能源协同优化提供可能[6]。

目前,基于电、气、热等多种能源载体的多能源系统耦合架构和运行方法已有大量研究[7-8]。文献[7]提出的能量枢纽建模方法可以对不同能源系统的耦合关系进行建模。文献[8]提出了包含能源转换和传输的多能源系统稳态潮流模型。文献[9]提出了一种基于有限元节点法的电—气耦合微能源网能量流计算方法。由于可再生能源的利用给电网带来了大量的不确定性和随机性,并且加上风光发电的反调峰特性,使得一些地区出现了明显的弃风弃光现象,造成经济损失和能源浪费。多能源系统能否高效、可靠、经济、环境友好地运行,取决于该系统的设备选型、设备容量及运行策略的整体优化。

现有研究大多是关于能量枢纽的优化运行与最优潮流等问题,而较少地关注能量枢纽组件的型号选择与容量设计。文献[10]为了确定枢纽可用组件的最优数量和容量,在气—电混合区域中提出了互联能量枢纽的规划问题。文献[11]研究了能量枢纽的扩展规划问题。文献[12]提出了一个考虑能量枢纽可靠性和经济性以确定枢纽最优组件的最优设计模型,研究了在单点故障下最大化失负荷概率等指标。文献[13]提出了一种分析和计算多能源载体供应可靠性期望和能量未供应期望的模型。文献[14]采用最大流最小割法确定多个能量枢纽耦合架构间的传输容量。针对含不确定因素的最优容量配置问题,文献[15]将可再生能源的不确定性用间隔数表示,采用证据推理方法解决综合能源系统的最优容量配置问题。文献[16]基于机会约束规划对用户侧综合能源系统进行最优容量配置。文献[17]利用随机规划对热电联产(CHP)系统进行优化配置,并采用双层规划方法求解。文献[18]提出气—电系统联合扩展规划,引入决策分析以解决系统可靠性、市场不确定性及需求响应影响等问题。文献[19]提出一种冷热电联供系统的三级协同整体优化方法,采用粒子群算法确定设备的型号、容量及最优运行结果。文献[20]提出了电、气、直热网络多目标优化模型,应用改进目标削减方法求解,实现综合能源系统各参与单元的利益协调。

综上所述,现有研究成果主要从多能源系统设备选型、容量配置和运行策略3个角度建立优化模型,而未对这3个方面进行综合考虑,进而整体优化设计能量枢纽。传统机组组合模型以系统运行费用和启动费用两者形成的综合成本最低为优化目标,采用确定性的负荷预测数据,未考虑机组故障的随机性和电力系统的可靠性。而能量枢纽的配置问题不仅应考虑经济性问题,也应考虑系统上述可能存在的风险问题。

针对上述问题,本文在优化配置过程中考虑能量枢纽的可靠性,提出能量枢纽可靠性指标,将容量优化配置与运行策略相结合,设计枢纽组件的类型和容量,兼顾能量枢纽的整体优化设计,使能源的可靠性供应满足预期要求,同时使规划期的成本最小。首先,给出能量枢纽模型,建立计及可靠性的能量枢纽优化配置模型。其次,根据优化策略,提出基于双层优化的能量枢纽最优设计求解方法。最后,对算例进行仿真,验证了所提模型与优化策略的有效性。

1 能量枢纽建模

1.1 能量枢纽能源转换模型

能量枢纽是对相互协调的多能源系统的建模,代表能源生产、消耗和传输设备之间的交互[21]。能量枢纽通常包含三种基本组件:①能量传输设备, 将输入的能量直接传输到输出侧,不进行能量形式转换,如电缆、架空线、管道等;②能量转换设备, 将不同能源形式进行相互转换,如燃气轮机、内燃机、电动机、燃料电池等;③储能装置,如蓄电池、燃料电池、储热罐等。本文设计的能量枢纽模型包括风机、变压器、CHP机组、燃气锅炉、电/热储能等设备。典型能量枢纽实例如图1所示。

图1 典型能量枢纽模型结构Fig.1 Structure of a typical energy hub

从数学角度看,能量枢纽可以被视为一个两端口网络[22]。输入能量枢纽的电能、天然气等多种形式的能量经过转换、存储装置得到系统的输出(如电、热、冷)。输入输出之间的函数关系可以表示为:

L=CP

(1)

即

式中:P为能量枢纽输入列向量;L为能量枢纽输出列向量;C为耦合矩阵,表示能量枢纽输入输出间的分配与转换关系。

1.2 计及储能的能量枢纽模型

能量存储单元实现能量跨时段转移并协调网内“源—荷”间不平衡,具有削峰填谷和抑制可再生能源波动的作用,促进供能系统经济高效运行[23]。通过各种形式的能源存储可以确保能源转化过程的进行,除了水泵、电池、飞轮等形式的能源存储,热储能也是一种重要的储能形式。提高负荷可控性的内在存储的方法现已出现,如具有热惯性的家用电器控制策略和预期与电网连接的大规模电动汽车。

对于图1所示的系统数学模型,输入电、气两种能源形式,输出为电需求、热需求,矩阵形式表示为:

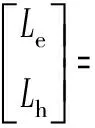
(2)

2 计及可靠性的能量枢纽优化配置模型

2.1 目标函数

根据图1所示的能量枢纽结构,枢纽主要组件是能源转换和存储装置。枢纽规划设计问题的目标函数是使负荷供应的总安装成本、总运行成本与计及可靠性约束的惩罚成本之和最小。

min(CI+CO+CP)

(3)

式中:CI为总安装成本;CO为总运行成本;CP为计及可靠性的惩罚成本。

总安装成本包括能源转换器和储能装置安装成本,可表示为:

(4)

式中:k为机组编号;i和j分别为能源转换与存储装置类型;CIi,CIj,Pi,Pj分别为能源转换装置与存储装置的单位容量安装成本与安装容量,其中,安装容量可在备选机组中进行选择;Iik和Ijk分别为能源转换与存储装置的安装状态,是一个0-1变量,0表示该装置未被用于枢纽中,1表示该装置参与枢纽运行;r0为年折旧率;m为规划期年限。此处,能源转换装置包括变压器、CHP、燃气锅炉,储能装置包括电储能、热储能装置。

总运行成本是各能源转换、存储设备单位容量运行成本与输出功率的乘积,可表示为:

(5)

式中:COi,COj,pi,pj分别为能源转换装置与存储装置的单位容量运行成本与输出功率。

惩罚成本可表示为:

Cp=CEENSCVOLL

(6)

(7)

式中:CEENS和CVOLL分别为能量未供应期望和失负荷值,失负荷值为一给定值;ps为第s个场景负荷未供应概率;DLt为t时刻未供应能量。本文假设能量枢纽仅发生单点故障。

IγFORγ(1-FORγ)-1p0

(8)

式中:Iγ为机组γ的安装状态;FORγ为第γ个组件的强制中断率;θ为全部组件的集合;w为未发生强制中断的组件集合;FORw为第w个组件的未强制中断率;p0为未发生故障机组的概率乘积。此处,由于目标函数中存在的安装状态和输出功率的乘积为非线性模型,使用Big-M方法将其线性化。

2.2 约束条件

1)电、热平衡分别为:

(9)

(10)

2)设备运行约束

能源传输转换设备的输入限制为:

(11)

3)储能约束

(12)

(13)

(14)

(15)

(16)

4)分配系数

(17)

式中:vc为某种形式能源分配到不同能源转换装置的分配系数;c为能源转换装置编号。

5)负荷旋转备用约束

为应对系统突发状况,含高渗透率可再生能源的多能源系统在优化配置中需要为系统预留部分旋转备用,并在能量枢纽中起到修正可靠性指标的作用。

(18)

6)可靠性约束

由CEENS和失负荷时间期望指标CLOLE体现。

CEENS≤CEENS,max

(19)

(20)

式中:CEENS,max为能量未供应期望指标值上限;CLOLE,max为失负荷时间期望值上限;DLST为失负荷持续总时间。

能源枢纽的可靠性主要由元件参数、运行参数和网络内部拓扑等因素决定。而各机组的布放位置及设备的接线与运行方式是影响能源枢纽内部网络拓扑结构的关键因素,该因素主要是在能源枢纽规划问题中建设施工过程应重点考虑的工程问题。

3 基于双层优化的能量枢纽最优设计方法

3.1 双层优化模型

本文将能量枢纽优化设计问题分解为能量枢纽设备容量配置和系统能量分配问题进行求解。传统能量枢纽容量配置和能量分配单独求解的模型使优化结果容易陷入局部最优解。由于双层规划可以同时考虑能量枢纽配置和运行调度,第1层机组容量优化配置结果可作为第2层运行优化能量分配的数据基础,第2层能量分配结果可为第1层机组容量优化配置进行反馈验证,通过上下层间的优化迭代最终求得全局最优解。本文构建的基于双层优化的能量枢纽优化设计模型求解流程如图2所示。该系统优化配置涉及枢纽结构优化和运行变量优化,第1层优化变量为能量枢纽各组件的容量变量,即CHP机组台数、锅炉台数、电/热储能机组数,第2层优化变量为能量枢纽各组件的出力。

图2 能量枢纽双层优化设计方法框图Fig.2 Two-layer optimization method of energy hub

3.2 优化策略

系统优化设计策略主要用于确定各时刻机组的出力,对运行费用有直接影响。由于系统负荷对运行可靠性的要求较高,因而从电网购电是多能源系统的主要供能电源,而可再生能源则是作为补充电源缓解和减轻发电厂排放的污染物对环境的危害。但是考虑到可再生能源的随机性,本文设定如下优化策略:优先考虑风力发电,最大程度地利用可再生能源发电满足负荷用电的基本需求;当风能由于其随机性不能满足负荷用电时,根据当前时段电价和蓄电池的荷电状态,确定CHP出力、燃气锅炉出力、电网直接供电大小及其顺序;如果CHP发电量仍不能满足用电需求时,判断储能装置放电条件,若满足则采用蓄电池放电来满足系统中的瞬时短缺能量;当蓄电池的剩余电量不能满足用电需求时,从大电网购电。通过计算系统成本,也可切除不重要负荷,并计入电力不足指标。该优化策略用于下层优化运行模型迭代求解验证。

3.3 优化模型求解

由第2节可知,基于可靠性的能量枢纽规划问题是一个混合整数线性规划(MILP)问题。根据3.2节提出的优化策略,上层采用精英保留策略遗传算法,使用自适应交叉率、突变率对遗传算法进行改进。由于下层优化变量非线性且维数高,采用具有参数设定少、求解速度快等特性的粒子群算法进行下层运行优化的能量分配问题求解,使用MATLAB进行仿真,算法流程如图3所示。

图3 算法流程图Fig.3 Flow chart of algorithm

算法求解步骤如下。

步骤1:输入系统参数及负荷数据,初始化粒子群参数。

步骤2:对决策变量进行染色体编码。

步骤3:上层规划优化,产生上层规划遗传算法初始种群,即随机产生N个D维设备容量变量组成的初始种群,令迭代次数t=1。

步骤4:下层规划优化,对于每一个上层规划的初始种群,产生下层规划初始种群。

步骤5:根据下层优化模型,使用粒子群算法进行机组优化运行计算,获得最优目标函数值。

步骤6:将下层优化结果返回上层规划,计算上层规划模型。

步骤7:进行遗传操作,选择、交叉、变异,产生新种群。

步骤8:针对各粒子,结合3.2节提出的优化策略分别仿真计算多能源系统全年的运行情况,得到与各微粒对应的系统可靠性指标,进行可靠性检验。

步骤9:判断是否满足最大迭代次数，即最优个体最少保留代数或遗传代数,若是则停止迭代,输出能量枢纽优化设计结果;否则继续执行步骤5至步骤8。

4 算例分析

4.1 基础数据

本文分别给出两种变压器、三种CHP机组、三台燃气锅炉及两类电热储能装置用于设备选型,系统结构如图1所示,能量枢纽组件的数量不做限制。设定规划年限为10 a,年利率为5%。各转换器及储能装置的额定容量、效率、安装成本、运行维护成本等参见附录A表A1至表A4。

算例选取的典型日24 h的电、热负荷需求、分时电价与天然气价格分别参见附录A图A1至图A2。其中,售电价格是购电价格的1.5倍。

本文中风机容量不参与优化,假设风力发电的额定输出功率为400 kW,始终以风机最大出力消纳风电,安装成本为9元/kW。风电预测功率如附录A图A3所示。电、热失负荷值分别为30元/(kW·h)和18元/(kW·h)。

4.2 优化配置结果分析

为了分析多能源耦合、储能单元、负荷供应可靠性约束集成作用的效果,设定了4种算例:算例1采用传统能源供应网络,各能源系统单独运行,即电负荷由电网购电满足,热负荷仅由燃气锅炉产生,无储能设备;算例2为电、气、热多能源耦合模式,无储能设备,考虑组件随机中断;算例3在算例2的基础上加入储能装置;算例4考虑储能影响,并考虑枢纽组件全部充分可用。通过求解上述优化问题,得到不同情景下选择的能源转换和存储装置,能量枢纽优化配置结果及各算例成本分别如表1和表2所示。

由表1可知,算例2相比算例1,由于CHP的投资成本明显高于传统发电机组,使得算例系统投资成本增加,而因为CHP燃料消耗少、运行效率高,故运行成本显著减小,总成本降低。算例3和算例4考虑储能作用,使系统安装成本增加、运行成本显著降低,通过储能减缓了风电的不确定性。算例4由于所有组件充分可用,投资成本和运行成本比算例3少,可靠性惩罚成本可以近似忽略。

表1 能量枢纽优化配置结果Table 1 Optimal configuration of energy hub for different cases

表2 各算例成本值Table 2 Cost of energy hub under different cases

使用上文提到的可靠性约束将产生不同的可靠性水平。电储能荷电状态达到下限之前预先从电网购电满足电负荷平衡。由于使用储能单元,系统的可靠性水平显著增加。另一方面,电负荷比热负荷的失负荷值高,这也导致电负荷的可靠性水平比热负荷高。为了阻止在每种能源转换和存储单元可能的中断之后产生任何负荷损失,失负荷期望这一可靠性约束及目标函数中相应的惩罚成本使得枢纽维持更高的备用能量。

各算例可靠性指标如表3所示,表中CLOLE,e和CLOLE,h分别为失负荷时间期望的电能指标和热能指标;CEENS,e和CEENS,h分别为能量未供应期望的电能指标和热能指标。由此可以得出,传统供能网络的可靠性最差;通过对比算例2和算例3可以看出,组件随机中断算例下储能单元的加入,使系统的可靠性水平显著提高;通过对比算例3和算例4可以看出,算例4所有组件充分可用,即将可靠性约束在一定范围内可以降低系统的失负荷时间期望与能量未供应期望,表明系统可靠性增强。因此,结果证明了计及可靠性的能量枢纽优化配置方法的有效性,通过可靠性指标的大小可以说明考虑可靠性约束的能量枢纽优化模型有利于系统可靠性的提升。

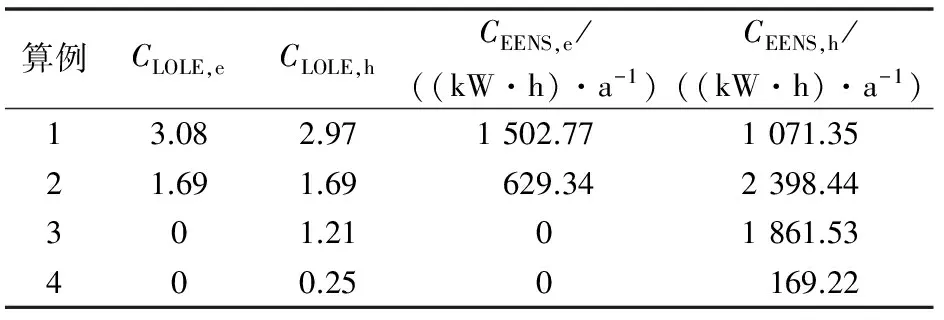
表3 各算例可靠性指标值Table 3 Reliability indices under different cases

在算例3的基础上,改变风机容量,设定算例3a、算例3b、算例3c风机安装容量分别为200,400,600 kW,风机安装容量对可靠性指标的影响如表4所示。由表4可以看出,电负荷的失负荷时间期望和能量未供应期望均小于热负荷。随着风机安装容量的增加,可靠性指标均降低,表明系统可靠性增强。

表4 风机安装容量对可靠性指标的影响Table 4 Effect of installation capacity of wind turbine on reliability indices

4.3 典型日含储能的能量枢纽能量分配结果分析

各时段机组出力,即能量枢纽电能平衡情况如图4所示。在夜间负荷需求较低时,风力所发部分电力借助储能设备进行存储。18:00—21:00时段逐渐上升为用电高峰时段,向电网购电价格较高,CHP接近满发,同时由储能设备释放电能供给电力需求,缓解高峰时段发电需求,由于此时热负荷不高,CHP产生的多余热量被热储能装置存储;19:00—20:00用电高峰时段发生负荷削减,该用电行为在实现削峰的同时实现了经济性最优;22:00—06:00用电量下降,逐渐过渡到谷值时段,首先最大限度消纳风电,不足由CHP发电、蓄电池放电及从电网购电补充,到凌晨时段电网购电价格较低,该时段的电力需求主要靠风电供应和从电网购电,过剩电能由电储装置进行存储,提高了系统的风电消纳能力,使得净负荷波动性变得平缓,此时段热负荷主要由储热装置和燃气锅炉供给。由此可见,多能流耦合互补促进了可再生能源消纳,储能实现了不同时段的能量转移,有助于削峰填谷。

图4 能量枢纽能量分配结果Fig.4 Energy distribution results of energy hub

5 结语

本文基于多能互补和网络互济,提出了一种计及可靠性的能量枢纽最优规划与运行双层模型,结合优化策略确定了能量枢纽最优容量配置与能量分配结果。基于能量枢纽的多种能源联合规划设计相比传统分供形式,供能方式灵活,并提高了供能的可靠性与系统的经济性。通过利用储能装置,实现了削峰填谷。

再者,组件随机中断被考虑在优化问题中,反映不同的供给可靠性对多能源系统经济性的影响。使用提出的计及可靠性的能量枢纽优化设计模型可以帮助枢纽决策者确定满足负荷需求的最优设备容量和数量。在提高负荷供应可靠性的同时,能够减少能源供应成本。仿真结果验证了计及可靠性的能量枢纽规划模型的可行性和有效性。此外,由于风机出力具有不确定性,在规划模型中考虑风机容量的优化将使得可靠性分析更为复杂,对于该部分不确定性因素分析将作为下一阶段能量枢纽优化运行的研究重点。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 曾鸣,杨雍琦,刘敦楠,等.能源互联网“源-网-荷-储”协调优化运营模式及关键技术[J].电网技术,2016,40(1):114-124.

ZENG Ming, YANG Yongqi, LIU Dunnan, et al. “Generation-grid-load-storage” coordinative optimal operation mode of energy internet and key technologies[J]. Power System Technology, 2016, 40(1): 114-124.

[2] 曾鸣,杨雍琦,李源非,等.能源互联网背景下新能源电力系统运营模式及关键技术初探[J].中国电机工程学报,2016,36(3):681-691.

ZENG Ming, YANG Yongqi, LI Yuanfei, et al. The preliminary research for key operation mode and technologies of electrical power system with renewable energy sources under energy internet[J]. Proceedings of the CSEE, 2016, 36(3): 681-691.

[3] 孙宏斌,潘昭光,郭庆来.多能流能量管理研究: 挑战与展望[J].电力系统自动化,2016,40(15):1-8.DOI:10.7500/AEPS20160522006.

SUN Hongbin, PAN Zhaoguang, GUO Qinglai. Energy management for multi-energy flow: challenges and prospects[J]. Automation of Electric Power Systems, 2016, 40(15): 1-8. DOI: 10.7500/AEPS20160522006.

[4] 甘霖,陈瑜玮,刘育权,等.含可再生能源的微网冷-热-电多能流协同优化与算例分析[J].电力自动化设备,2017,37(6):275-281.

GAN Lin, CHEN Yuwei, LIU Yuquan, et al. Coordinative optimization of multiple energy flows for microgrid with renewable energy resources and case study[J]. Electric Power Automation Equipment, 2017, 37(6): 275-281.

[5] 余晓丹,徐宪东,陈硕翼,等.综合能源系统与能源互联网简述[J].电工技术学报,2016,31(1):1-13.

YU Xiaodan, XU Xiandong, CHEN Shuoyi, et al. Brief review to integrated energy system and energy internet[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 1-13.

[6] 吴聪,唐巍,白牧可,等.基于能源路由器的用户侧能源互联网规划[J].电力系统自动化,2017,41(4):20-28.DOI:10.7500/AEPS20160802010

WU Cong, TANG Wei, BAI Muke, et al. Energy router based planning of energy internet at user side[J]. Automation of Electric Power Systems, 2017, 41(4): 20-28. DOI: 10.7500/AEPS20160802010.

[7] GEIDL M, ANDERSSON G. Optimal coupling of energy infrastructures[C]// 2007 IEEE Lausanne Power Tech, July 1-5, 2007, Lausanne, Switzerland： 1398-1403.

[8] GEIDL M, ANDERSSON G. Optimal power flow of multiple energy carriers[J]. IEEE Transactions on Power Systems, 2007, 22(1): 145-155.

[9] 马腾飞,吴俊勇,郝亮亮.含冷热电三联供的微能源网能量流计算及综合仿真[J].电力系统自动化,2016,40(23):22-27.DOI:10.7500/AEPS20160426005.

MA Tengfei, WU Junyong, HAO Liangliang. Energy flow calculation and integrated simulation of micro-energy grid with combined cooling heating and power[J]. Automation of Electric Power Systems, 2016, 40(23): 22-27. DOI: 10.7500/AEPS20160426005.

[10] SALIMI M, GHASEMI H, ADELPOUR M, et al. Optimal planning of energy hubs in interconnected energy systems: a case study for natural gas and electricity[J]. IET Generation, Transmission & Distribution, 2015, 9(8): 695-707.

[11] ZHANG X, SHADIDEHPOUR M, ALABDULWAHAB A, et al. Optimal expansion planning of energy hub with multiple energy infrastructures[J]. IEEE Transactions on Smart Grid, 2015, 6(5): 2302-2311.

[12] SHAHMOHAMMADI A, MORADI-DALVAND M, GHASEMI H, et al. Optimal design of multicarrier energy systems considering reliability constraints[J]. IEEE Transactions on Power Delivery, 2015, 30(2): 878-886.

[13] KOEPPEL G, ANDERSSON G. Reliability modeling of multi-carrier energy systems[J]. Energy, 2009, 34(3): 235-244.

[14] ZHANG X, CHE L, SHAHIDEHPOUR M, et al. Reliability-based optimal planning of electricity and natural gas interconnections for multiple energy hubs[J]. IEEE Transactions on Smart Grid, 2017, 8(4): 1658-1667.

[15] WEI F, WU Q H, JING Z X. Optimal capacity configuration for the integrated energy system using interval optimization[C]// IEEE Innovative Smart Grid Technologies-Asia, November 28-December 1, 2016, Melbourne Australia: 190-195.

[16] JIA C, BAI M, ZHANG C, et al. Optimal configuration of user side integrated energy system based on chance constrained programming[C]// Probabilistic Methods Applied to Power Systems (PMAPS), October 16-20, 2016, Beijing, China: 1-8.

[17] BENAM M R, MADANI S S, ALAVI S M, et al. Optimal configuration of the CHP system using stochastic programming[J]. IEEE Transactions on Power Delivery, 2015, 30(3): 1048-1056.

[18] WANG Dongxiao, QIU Jing, MENG Ke, et al. Coordinated expansion co-planning of integrated gas and power systems[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(3): 314-325.

[19] 赵峰,张承慧,孙波,等.冷热电联供系统的三级协同整体优化设计方法[J].中国电机工程学报,2015,35(15):3785-3793.

ZHAO Feng, ZHANG Chenghui, SUN Bo, et al. Three-stage collaborative global optimization design method of combined cooling heating and power[J]. Proceedings of the CSEE, 2015, 35(15): 3785-3793.

[20] KOU Y N, ZHENG J H, LI Zhigang, et al. Many-objective optimization for coordinated operation of integrated electricity and gas network[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(3): 350-363.

[21] GEIDL M, KOEPPEL G, FAVRE-PERROD P, et al. Energy hubs for the future[J]. IEEE Power and Energy Magazine, 2007, 5(1): 24.

[22] 王毅,张宁,康重庆.能源互联网中能量枢纽的优化规划与运行研究综述及展望[J].中国电机工程学报,2015,35(22):5669-5681.

WANG Yi, ZHANG Ning, KANG Chongqing. Review and prospect of optimal planning and operation of energy hub in energy internet[J]. Proceedings of the CSEE, 2015, 35(22): 5669-5681.

[23] 李洋,吴鸣,周海明,等.基于全能流模型的区域多能源系统若干问题探讨[J].电网技术,2015,39(8):2230-2237.

LI Yang, WU Ming, ZHOU Haiming, et al. Study on some key problems related to regional multi energy system based on universal flow model[J]. Power System Technology, 2015, 39(8): 2230-2237.